Gregory coefficients のお話
${}$
まず, 自然数$n$に対し, $G_n$を以下のように定めます.
$$ G_n=\frac{1}{n!}\int_0^1x(x-1)\cdots(x-n+1)\,dx=\int_0^1\binom{x}{n}\,dx$$
ただし$\ds\binom{x}{n}=\frac{x(x-1)\cdots(x-n+1)}{n!}$は一般化された二項係数です. これは$x$の多項式になります.
${}$
まず, この$G_n$の母関数を求めてみましょう. これは簡単で, $(1+z)^x$の$z$に関するTaylor展開が一般化された二項係数を用いて
$$ (1+z)^x=\sumn{0}\binom{x}{n}z^n$$
と表されることを用いれば, 両辺を$x:0\to1$で積分して
$$\beq
\sumn{0}G_nz^n&=&\int_0^1(1+z)^x\,dx\\[5pt]
&=&\frac{z}{\log(1+z)}
\eeq$$
と分かります.
${}$
これを利用すると, $N\geq2$に対し$\ds z=\log(1+z)\sum G_nz^n$ の両辺の$z^N$の係数を比較することで,
$$\beq
0&=&[z^N]\left(\log(1+z)\sum G_nz^n\right)\\[5pt]
&=&\sum_{k=0}^N\Big([z^{N-k}]\log(1+z)\Big)\left([z^k]\sum G_nz^n\right)\\[5pt]
&=&\sum_{k=0}^{N-1}\frac{(-1)^{N-k-1}}{N-k}G_k
\eeq$$
即ち$\ds\sum_{k=0}^{n-1}\frac{(-1)^kG_k}{n-k}=0$ ($n\geq2$)を得ます.
これは
$$\int_0^1\sum_{k=0}^{n-1}\frac{(-1)^k}{n-k}\binom{x}{k}\,dx=0$$
と書くと少し面白いですね.
${}$
ここで唐突に, 以下のような積分路に沿って関数$\ds f(z)=\frac{1}{(z-\alpha)\log z}$を積分することを考えてみましょう. ただし$\alpha\notin\R_{\leq0}\cup\{1\}$とし, 対数の偏角は$-\pi<\arg z<\pi$をとるものとします.
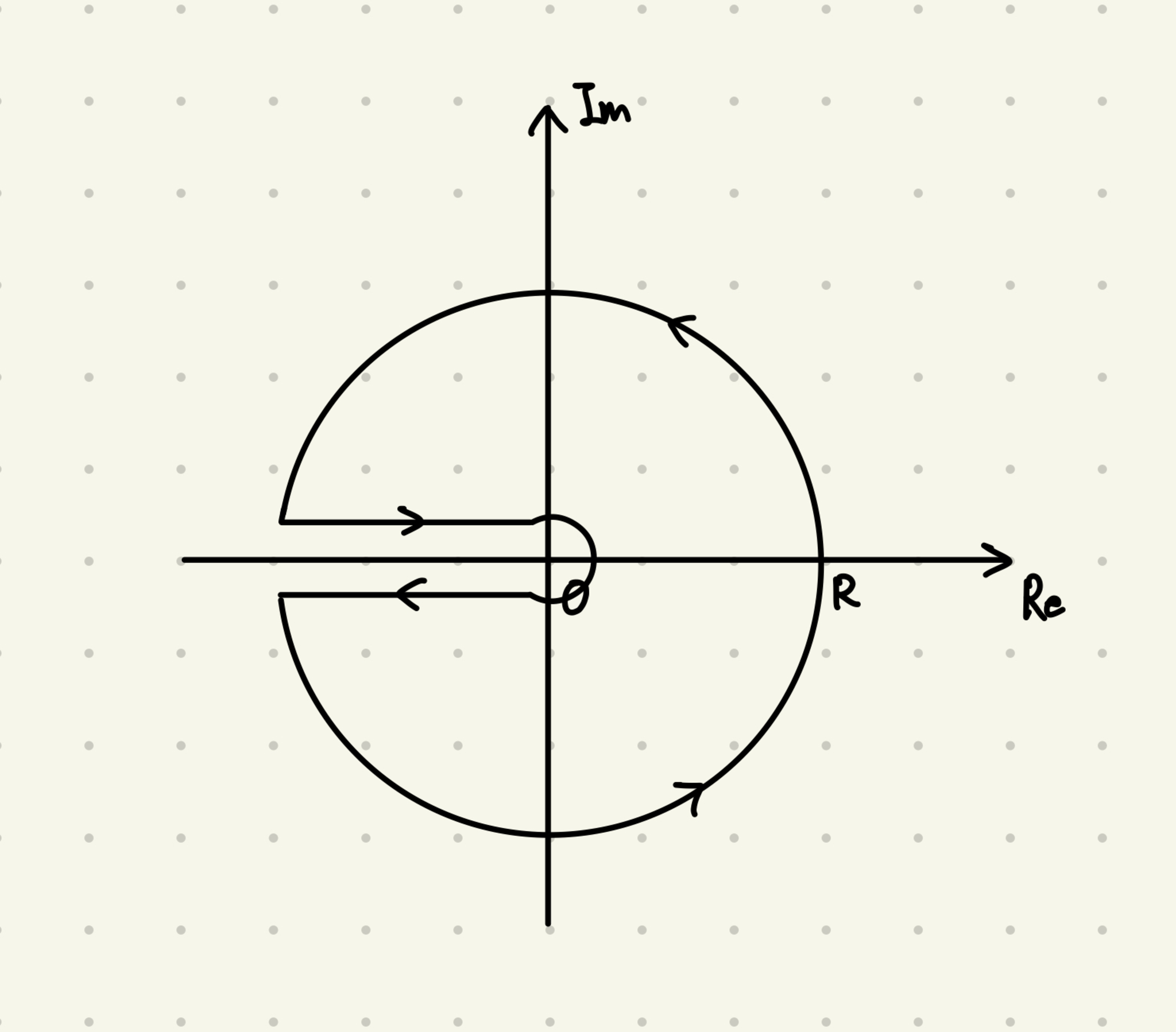 積分路
積分路
すると, $R\to\infty$で円弧上の積分は$0$になり, 原点周りの積分も$0$になりますから,
$$\beq
2\pi i\sum\mathrm{Res}f&=&\int_{-\infty+0i}^{+0i}f(z)\,dz+\int_{-0i}^{-\infty-0i}f(z)\,dz\\[5pt]
&=&\int_{\infty}^0f(e^{i\pi}x)\,e^{i\pi}dx+\int_0^\infty f(e^{-i\pi}x)\,e^{-i\pi}dx\\[5pt]
&=&-\int_0^\infty\frac{dx}{(x+\alpha)(\log x+i\pi)}+\int_0^\infty\frac{dx}{(x+\alpha)(\log x-i\pi)}\\[5pt]
&=&2\pi i\int_0^\infty\frac{dx}{(x+\alpha)(\log^2x+\pi^2)}
\eeq$$
極は$z=1,\alpha$であり,$\ds\mathrm{Res}_{z=1}f=\frac{1}{1-\alpha},\ \mathrm{Res}_{z=\alpha}f=\frac{1}{\log\alpha}$なので,
$$ \int_0^\infty\frac{dx}{(x+\alpha)(\log^2x+\pi^2)}=\frac1{\log\alpha}+\frac{1}{1-\alpha}$$
が結論されます.
${}$
ここで$\alpha=1+z$とするとなんと,
$$ \int_0^\infty\frac{dx}{(x+1+z)(\log^2x+\pi^2)}=\sumn{1}G_nz^{n-1}$$
となるではないですか!
両辺を$(n-1)$階微分して$z=0$とすることで,
$$ \int_0^\infty\frac{dx}{(x+1)^n(\log^2x+\pi^2)}=(-1)^{n-1}G_n$$
を得ます.
これは
$$ \int_0^\infty\frac{dx}{(x+1)^n(\log^2x+\pi^2)}=\int_0^1\left|\binom{x}{n}\right|\,dx$$
と書くと面白いですね.
${}$
最後になりますが, 実はこの係数$G_n$はGregory coefficientsと呼ばれるものなのでした. ( Wikipedia 参照)
${}$
読んでくださった方, ありがとうございました.
${}$
${}$
