積分解説5 ∫[0,π/2]((sin(x+e^((π/2)cotx)))/sinx)dx
${}$
この記事では, 以下の積分の解説をしようと思います.
${}$
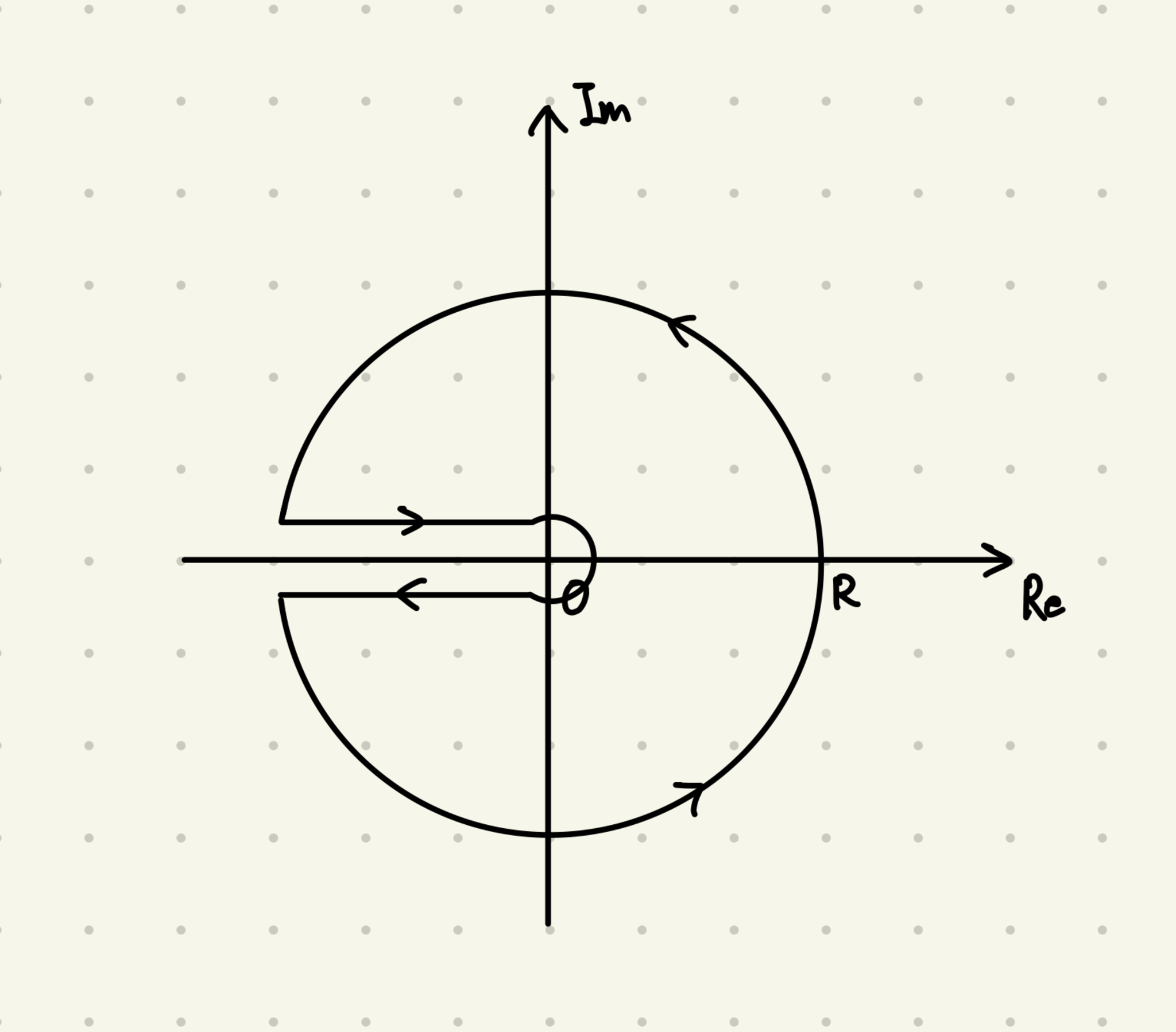 積分路
積分路
上のような積分路に沿った, 関数
$$ f(z)=\frac{e^{-\sqrt{z}}}{z\log z}=\frac{\exp(-\exp(\frac12\log z))}{z\log z}$$
の積分を考えます. ただし対数の偏角は$-\pi<\arg z<\pi$ととることにします.
すると, 前回と全く同様に, 円弧上の積分は(√をとっているお陰で)$R\to\infty$で$0$になり, 原点周りも$0$になるので, 積分は
$$\beq
&&\int_{-\infty+0i}^{+0i}f(z)\,dz+\int_{-0i}^{-\infty-0i}f(z)\,dz\\[5pt]
&=&\int_{\infty}^0f(e^{i\pi}x)\,e^{i\pi}dx+\int_0^\infty f(e^{-i\pi}x)\,e^{-i\pi}dx\\[5pt]
&=&-\int_0^\infty\frac{e^{-i\sqrt{x}}}{x(\log x+i\pi)}\,dx+\int_0^\infty\frac{e^{i\sqrt{x}}}{x(\log x-i\pi)}\,dx\\[5pt]
&=&\int_0^\infty\frac{2i\sin\sqrt{x}\ \log x+2\cos\sqrt{x}\cdot i\pi}{x(\log^2x+\pi^2)}\,dx\\[5pt]
&=&2i\int_0^\infty\frac{\sin(\sqrt{x}+\mathrm{arccot}\frac{\log x}{\pi})}{x\sqrt{\log^2x+\pi^2}}\,dx
\eeq$$
となり, 留数は$\ds\mathrm{Res}_{z=1}f=\frac1{e}$なので,
$$\int_0^\infty\frac{\sin(\sqrt{x}+\mathrm{arccot}\frac{\log x}{\pi})}{x\sqrt{\log^2x+\pi^2}}\,dx=\frac{\pi}{e}$$
となります.
ここで$\ds x\mapsto e^{\pi\cot x}$と置換することで題意の積分を得ます.
${}$
読んでくださった方, ありがとうございました.
${}$
${}$
