【九州大学2021年度前期入試数学(理系)第3問】入試らしい微積分の問題
問題
座標平面上の点 $(x,y)$ について，次の条件を考える．
条件: すべての実数 $t$ に対して $y\le e^t-xt$ が成立する． $\cdots\cdots\cdots (*)$
以下の問いに答えよ．必要ならば $\displaystyle\lim_{x\to +0}x\log x=0$ を使ってよい．
条件 $(*)$ をみたす点 $(x,y)$ 全体の集合を座標平面上に図示せよ．
条件 $(*)$ をみたす点 $(x,y)$ のうち，$x\geqq 1$ かつ $y\geqq 0$ をみたすもの全体の集合を $S$ とする．$S$ を $x$ 軸の周りに $1$ 回転させてできる立体の体積を求めよ．
解答解説
(1) の解答
$f(t)=e^t-xt-y$ とおくと，任意の実数 $t$ に対して $f(t)\geqq 0$ であるような $x,y$ の条件を求めればよい．$f'(t)=e^t-x$ であるので，次のようになる．
$x<0$ のとき，$\displaystyle\lim_{t\to-\infty}f(t)=-\infty$ であるので，条件を満たさない．
$x=0$ のとき，$f'(t)\geqq 0$ であるので，$f(t)$ は単調増加であり，$\lim_{t\to-\infty}f(t)=-y$ であるので，$-y\geqq 0$ すなわち $y\leqq 0$ であればよい．
$x>0$ のとき，$f'(t)=0$ とおくと $t=\log x$ であるので，次のような増減表ができる．
| $t$ | $\log x$ | ||
|---|---|---|---|
| $f'(t)$ | $-$ | $0$ | $+$ |
| $f(t)$ | $\searrow$ | $x-x\log x -y$ (最小) | $\nearrow$ |
よって，$x-x\log x-y\geqq 0$ すなわち，$y\leqq x - x\log x$ であればよい．$g(x)=x-x\log x$ とおくと，$g'(x)=1-\log x-1=-\log x$ であるので，増減表を書くと次のようになる．
| $x$ | $+0$ | $1$ | $+\infty$ | ||
|---|---|---|---|---|---|
| $g'(x)$ | $+$ | $0$ | $-$ | ||
| $g(x)$ | $0$ | $\nearrow$ | $1$ (最大) | $\searrow$ | $-\infty$ |
ここで，
\begin{align}
\lim_{x\to +0}g(x)&=\lim_{x\to +0}(x-x\log x)=0-0=0\\
\lim_{x\to +\infty}g(x)&=\lim_{x\to +\infty} x(1-\log x)=-\infty
\end{align}
である．よって，求める領域は次の通りである．
- 紫色の曲線の下(曲線を含む)
- $y$軸上の$y\leqq 0$ も含む
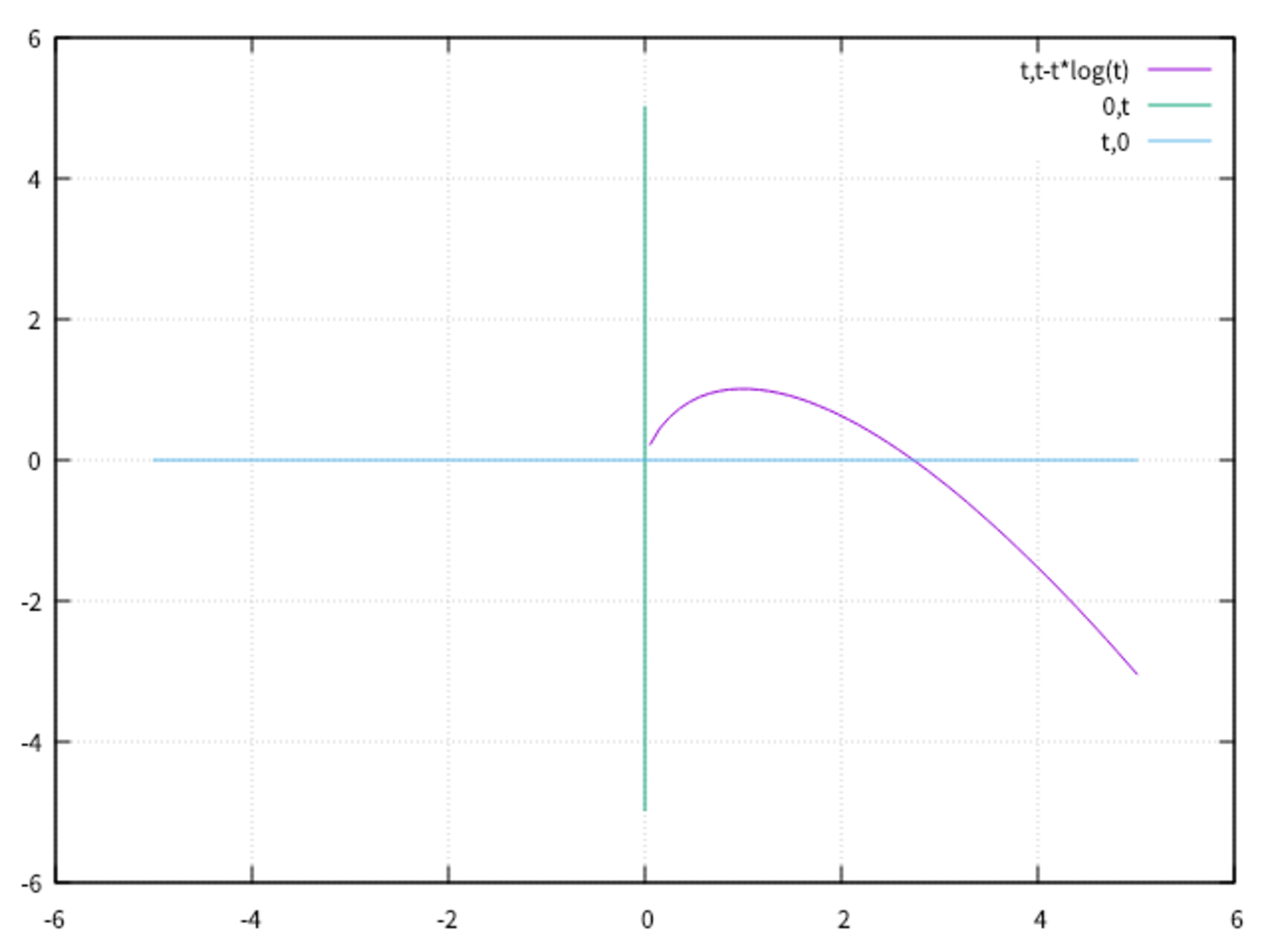求める領域
(2) の解答
$g(x)=0$ ($x>0$) とおく．このとき，$1-\log x=0$ すなわち $x=e$ である．よって，求める体積 $V$ は
\begin{align}
V&=\pi\int_{1}^{e}\{g(x)\}^2dx
=\pi\int_{1}^{e}x^2(1-\log x)^2 dx\\
&=\pi\left(\left[\frac{1}{3}x^3(1-\log x)^2\right]_{1}^{e}+\frac{2}{3}\int_{1}^{e}x^2(1-\log x)dx\right)\\
&=-\frac{\pi}{3}+\frac{2\pi}{3}\left(\left[\frac{1}{3}x^3(1-\log x)\right]_{1}^{e}+\frac{1}{3}\int_{1}^{e}x^2dx\right)\\
&=-\frac{\pi}{3}-\frac{2\pi}{9}+\frac{2\pi}{9}\left[\frac{1}{3}x^3\right]_{1}^{e}\\
&=-\frac{5\pi}{9}+\frac{2\pi}{27}(e^3-1)\\
&=\frac{(2e^3-17)\pi}{27}
\end{align}
となります．
感想
この問題も特に難しいところのない問題です．(2) の計算をどれだけスムーズに行うかが勝負です．
この記事を高評価した人
この記事に送られたバッジ
投稿者
