積分解説6 ∫[0,π/2]log(x^2+log^2cosx)dx
${}$
この記事では, 以下の美しい積分の証明をしようと思います. 実は積分botさんにあった積分なのですが, 現在積分botさんが不調のようですので, このような形での紹介となります. 証明はオリジナルです.
${}$
(証明)
以下, $a(1+e^{2ix})=2ae^{ix}\cos x$即ち
$$\log(a(1+e^{2ix}))=ix+\log(2a\cos x)\qquad(|x|<\hp)$$
に注意します. さらに, $\log z=\log |z|+i\arg z$ですから,
$$\log(x^2+\log^2(2a\cos x))=2\Re\log\log(a(1+e^{2ix}))$$
であることを利用していきます.
${}$
関数$\ds f(z)=\frac{\log\log z}{z-a}$を積分することを考えます. 円弧$z=a(1+e^{2ix})$に沿って積分すれば求める形を作ることができます.
ただし, $\log$の偏角を$|\arg z|<\pi$となるようにとります. 従って, $f(z)$は実軸上の区間$(-\infty,1]$を除いた領域で正則となります.
また, 区間$(0,1)$の近くでの$\log\log z$の値について, $0< x<1$に対して
$$\log\log(x\pm0i)=\log(\log\tfrac1x\pm0i)=\log\log\tfrac1x\pm i\pi$$
となることに注意します. ($x+0i$は実軸より無限小だけ上であることを表します.)
${}$
- $1< a$のとき
以下のような積分路をとります.
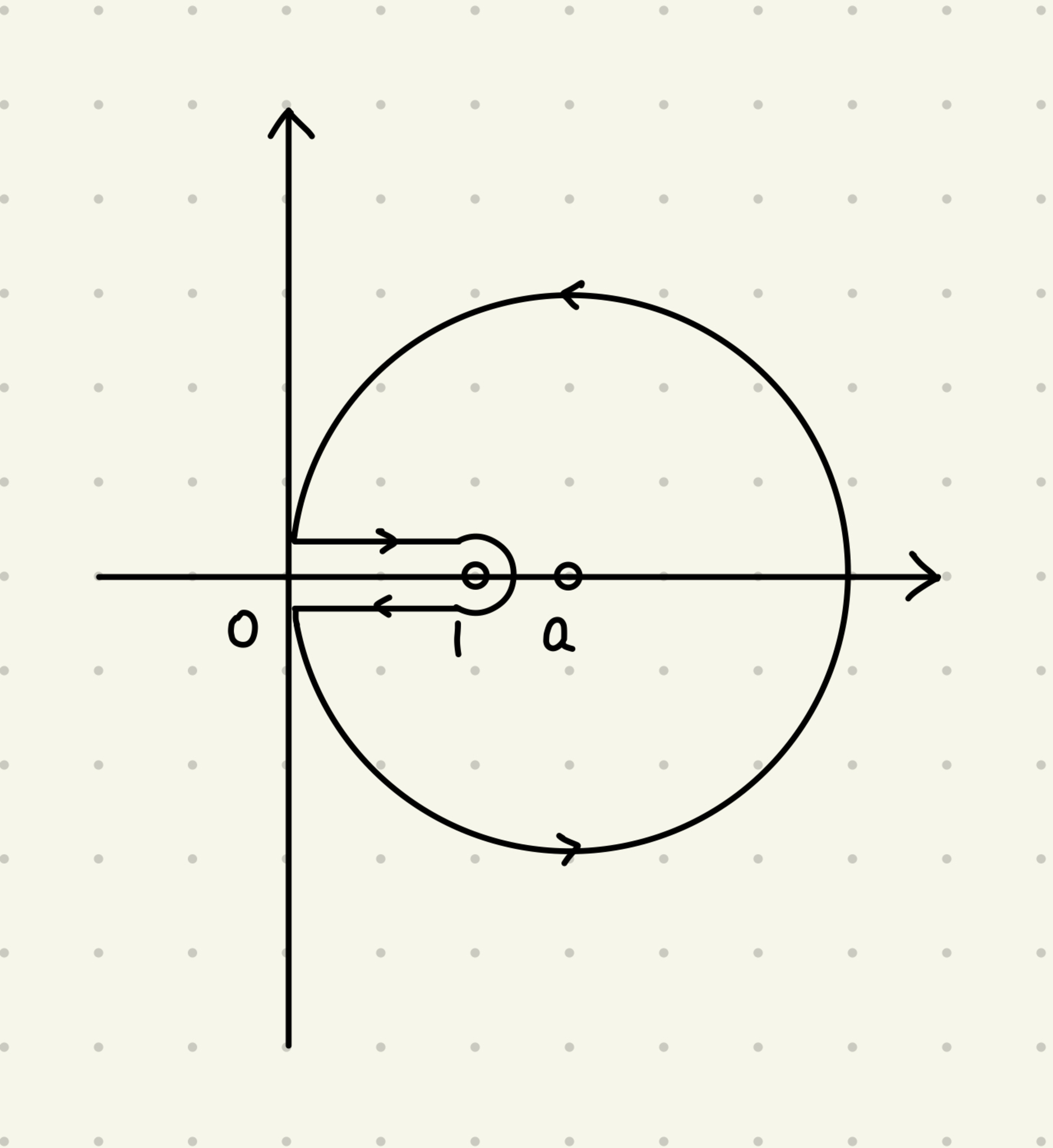 積分路1
積分路1
まず円弧上では, $z=a(1+e^{2ix})\quad(x:-\hp\to\hp)$と置換すれば,
$$\beq
\int_C f(z)\,dz&=&\int_{-\hp}^\hp\frac{\log\log(a(1+e^{2ix}))}{ae^{2ix}}2iae^{2ix}\,dx\\[5pt]
&=&2\int_0^\hp\log(x^2+\log^2(2a\cos x))\,dx
\eeq$$
となります. (虚部は明らかに奇関数であることを用いました.)
次に区間$(0,1)$の上下の積分は,
$$\beq
&&\left(\int_{+0i}^{1+0i}+\int_{1-0i}^{-0i}\right)f(z)\,dz\\[5pt]
&=&\int_0^1\frac{\log\log\tfrac1x+i\pi}{x-a}\,dx+\int_1^0\frac{\log\log\tfrac1x-i\pi}{x-a}\,dx\\[5pt]
&=&2\pi i\int_0^1\frac{dx}{x-a}\\[5pt]
&=&2\pi i\log(1-\tfrac1a)
\eeq$$
となります.
最後に, $z=a$での留数は$\mathrm{Res}_{z=a}f(z)=\log\log a$です.
以上より,
$$\beq
\int_0^\hp\log(x^2+\log^2(2a\cos x))\,dx&=&\pi\log\log a-\pi\log(1-\tfrac1a)\\[5pt]
&=&\pi\log\frac{\log a}{1-\tfrac1a}
\eeq$$
を得ます.
${}$
- $\frac12< a<1$のとき
以下のような積分路をとります.
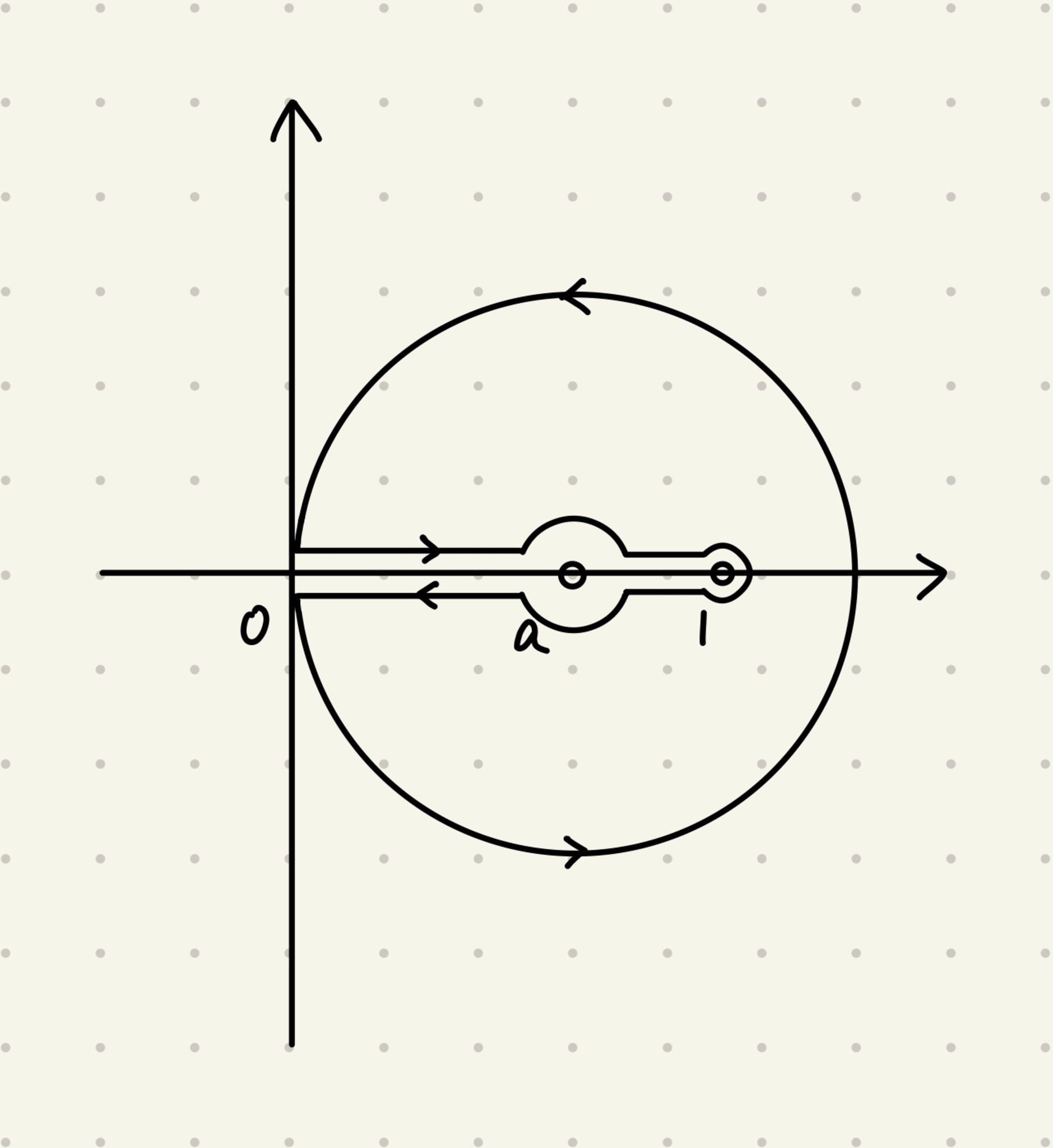 積分路2
積分路2
円弧上の積分は[1]と全く同様です.
今回は, 積分路上に極$a$が来ているので, 半径$\ep$の円に沿って積分し, $\ep\to0$とします. (つまり, 区間$(0,1)$上の主値積分をとっていることになります)
点$a$まわりの積分は, $\ds\frac{\log\log\tfrac1z}{z-a}$の分に関しては通常の留数と同じように考えられるので, $-2\pi i\log\log\tfrac1a$となります. $\ds\frac{\pm i\pi}{z-a}$の分に関しては, 今度は上側と下側で符号が変わるので, 打ち消しあって$0$になります.
最後に区間$(0,1)$の上下での主値積分は($\log\log x$が打ち消されることはもう分かるでしょう),
$$\beq &&2\pi i\ \mathrm{p.v.}\int_0^1\frac{dx}{x-a}\\[5pt] &=&2\pi i\lim_{\ep\to+0}\left(\int_0^{a-\ep}+\int_{a+\ep}^1\right)\frac{dx}{x-a}\\[5pt] &=&2\pi i\log(\tfrac1a-1) \eeq$$
以上より,
$$\int_0^\hp\log(x^2+\log^2(2a\cos x))\,dx=\pi\log\frac{\log\tfrac1a}{\tfrac1a-1}$$
を得ます.
${}$
- $0< a<\frac12$ のとき
以下のような積分路をとります.
 積分路3
積分路3
円弧上の積分と点$a$まわりの積分は上と全く同様です. 区間$(0,2a)$での主値積分は,
$$\mathrm{p.v.}\int_0^{2a}\frac{dx}{x-a}=0$$
ですので,
$$\int_0^\hp\log(x^2+\log^2(2a\cos x))\,dx=\pi\log\log\tfrac1a$$
を得ます.
${}$
以上の結果をまとめると,
となります.
ここで$a\to\frac12$として, (そもそもこれは極限を取るまでもなく[2]か[3]の議論に含めてしまえば良かったのですが)
$$\int_0^\hp\log(x^2+\log^2\cos x)\,dx=\pi\log\log2$$
を得ます. 綺麗ですね.
${}$
読んでくださった方, ありがとうございました.
${}$
${}$
