絶対三線座標系における2点間の距離公式

点$\mr{P}(a_1,b_1,c_1), \mr{Q}(a_2,b_2,c_2)$とする。$\mr{PQ}$を直径とする円を描く。$\mr{Q}$を通り、辺$\mr{BC},{CA}$と平行な直線を引き、この円との交点を$\mr{A'},\mr{B'}$とする。

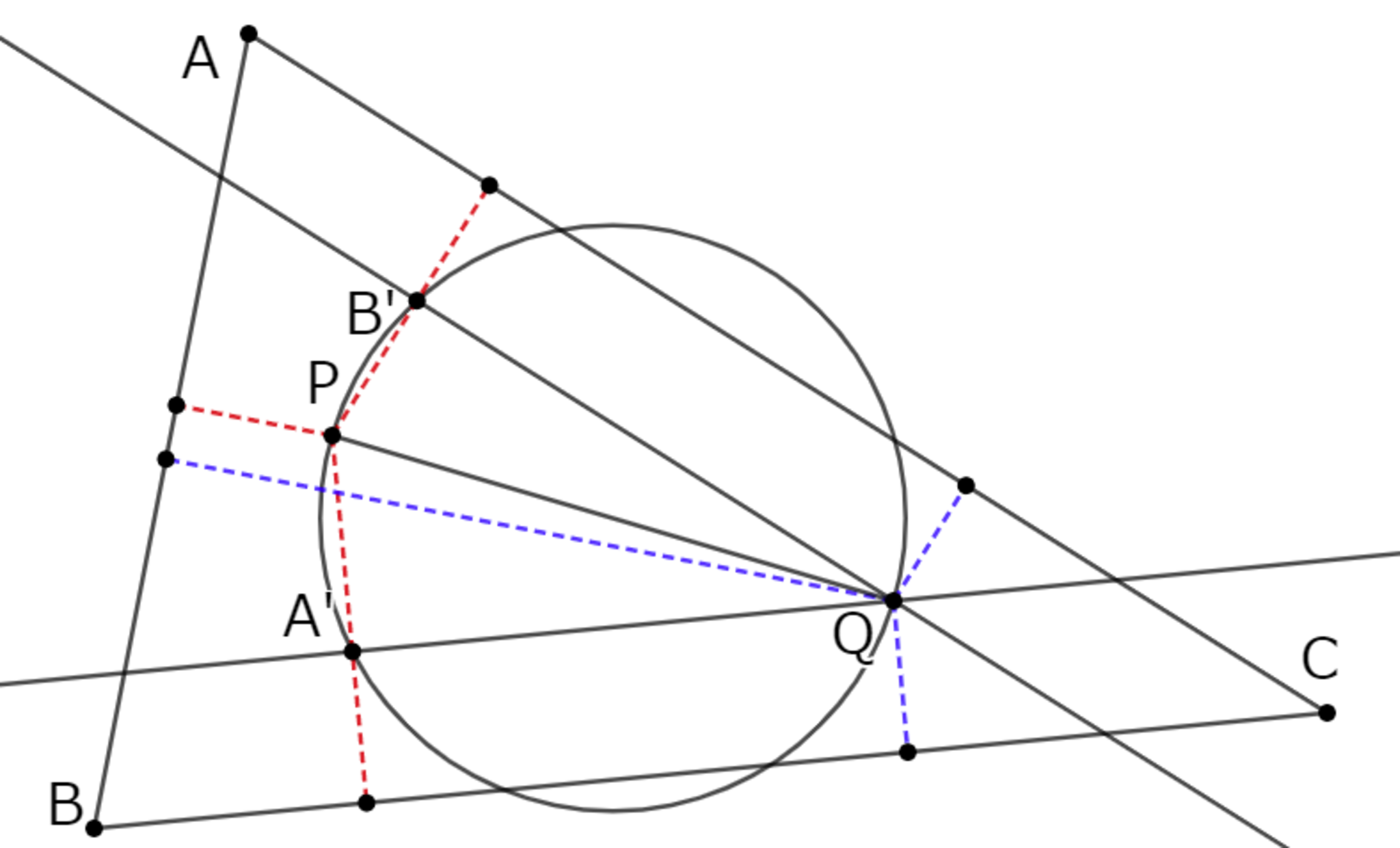
このとき、$\mr{A'B'}^2=\mr{PA'}^2+\mr{PB'}^2-2\mr{PA'}\cdot\mr{PB'}\cos\angle\mr{A'PB'}$である。
$\mr{PA'}=|a_1-a_2|$, $\mr{PB'}=|b_1-b_2|$であって、$(a_1-a_2)(b_1-b_2)>0$のとき、$\angle\mr{A'PB'}=\pi-C$でありまた、$(a_1-a_2)(b_1-b_2)<0$のとき$\angle\mr{A'PB'}=C$となるから、いずれの場合でも
$$ \mr{PA'}\cdot\mr{PB'}\cos\angle\mr{A'PB'}=-(a_1-a_2)(b_1-b_2)\cos C $$
となる。$\alpha=a_1-a_2$, $\beta=b_1-b_2$とおくと、
$$ \mr{A'B'}^2=\alpha^2+\beta^2+2\alpha\beta\cos C $$
が従う。一方、$\dfrac{\mr{A'B'}}{\sin\angle\mr{AQB'}}=\mr{PQ}$であって、$\mr{P,Q}$の位置によっては$\angle\mr{A'QB'}=C, \pi-C$のいずれかなので、$\mr{A'B'}=\mr{PQ}\sin C$となる。
これらのことから、第一の公式が得られた。

さて、$aa_1+bb_1+cc_1=aa_2+bb_2+cc_2=2S$なので、
$$ a\alpha+b\beta+c\gamma=0 $$
である。なお、$c_1-c_2=\gamma$とした。第一の公式の両辺に$a^2b^2$を乗じて、
\begin{aligned} d^2a^2b^2\sin^2 C&=a^2b^2\alpha^2+a^2b^2\beta^2+ab\alpha\beta\cdot2ab\cos C \\ \dou\quad d^2 &= \frac{abc}{4S^2}\left(\frac{ab}{c}\alpha^2+\frac{ab}{c}\beta^2+\frac{\alpha\beta}{c}(a^2+b^2-c^2)\right) \\ &=\frac{abc}{4S^2}\left(\frac{1}{c}\bigl[ab\alpha^2+ab\beta^2+(a^2+b^2)\alpha\beta\bigr]-c\alpha\beta\right) \\ &=\frac{abc}{4S^2}\left(\frac{1}{c}(a\beta+b\alpha)(a\alpha+b\beta)-c\alpha\beta\right) \\ &=\frac{abc}{4S^2}\left(\frac{1}{c}(a\beta+b\alpha)(-c\gamma)-c\alpha\beta\right) \\ &=-\frac{abc}{4S^2}(a\beta\gamma+b\gamma\alpha+c\alpha\beta) \end{aligned}
となって、第二の公式が得られた。