[ラビットチャレンジ] 深層学習day1 レポート
はじめに
本稿は、E資格の受験資格の取得を目的としたラビットチャレンジの受講に伴うレポート記事である。
Section0：ニューラルネットワークの全体像
ディープラーニングとは、プログラムの代わりに、多数の中間層を持つニューラルネットワークを用いて、入力から目的とする出力値に変換する数学モデルを構築することを目的とする。
ニューラルネットワークとは、入力層、中間層、出力層からなる。重み$w$とバイアス$b$を最適化することにより誤差を最小化するパラメータを発見することでよりよいモデルができる。
Section1：入力層〜中間層
ニューラルネットワークは脳の神経構造を数学的にモデル化したもの。
入力データ$x_{1}, \cdots, x_{n}$を入力層が受け取ると、その入力データをニューロン間の結合強度を表現した重み$w_{1}, \cdots, w_{n}$により重み付けをした後、バイアス$b$を加えて和を取った値$u$を中間層が受け取る。
\begin{align*}
u = x_{1} w_{1} + x_{2} w_{2} + \cdots +x_{n} w_{n} + b
\end{align*}
これは$W = (w_{1}, \cdots, w_{n})^{T}, x = (x_{1}, \cdots, x_{n})^{T}$としたとき、以下のように書き換えられる。
\begin{align*}
u = Wx + b
\end{align*}
中間層はその受け取った値$U$に対して、後ほど記述する活性化関数$f$を適用した結果を出力する。
\begin{align*}
z &= f(u)
\end{align*}
■確認テスト
以下の数式をPythonで表現せよ
\begin{align*} u = x_{1} w_{1} + x_{2} w_{2} + x_{3} w_{3} + x_{4} w_{4} + + b \end{align*}
〇解答
u1 = np.dot(x, W1) + b1
出力例は以下の通り。
■確認テスト
「1_1_forward_propagation.ipynb」の中間層の出力を定義している箇所を抜き出せ。
〇解答
# 2層の総出力
z2 = functions.relu(u2)
※「1_1_forward_propagation.ipynb」の中間層の入力の定義は以下でされている。
# 2層の総入力
u2 = np.dot(z1, W2) + b2
Section2：活性化関数
ニューラルネットワークにおいて、次の層の出力の大きさを決める非線形関数のこと。
入力値により、次の層への信号のOn/Offや強弱を定める働きを持つ。
■確認テスト
線形と非線形の違いを図に書いて、簡易に説明せよ。
〇解答
わかりやすい図としては以下の通り。
線形の例
非線形の例
線形性とは、写像$f$が以下を満たすことをいう。
\begin{align}
f(x + y)
&= f(x) + f(y) \\
f(\alpha x)
&= \alpha f(x)
\end{align}
ステップ関数
閾値を越えたら発火する、以下で定義される関数。
\begin{align} f(x) &= \begin{cases} 1 & (x \ge 0) \\ 0 & (x < 0) \end{cases} \end{align}
def step_function(x):
return np.array(x > 0, dtype=np.int)
X = np.arange(-5.0, 5.0, 0.1)
Y = step_function(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.grid()
plt.show()
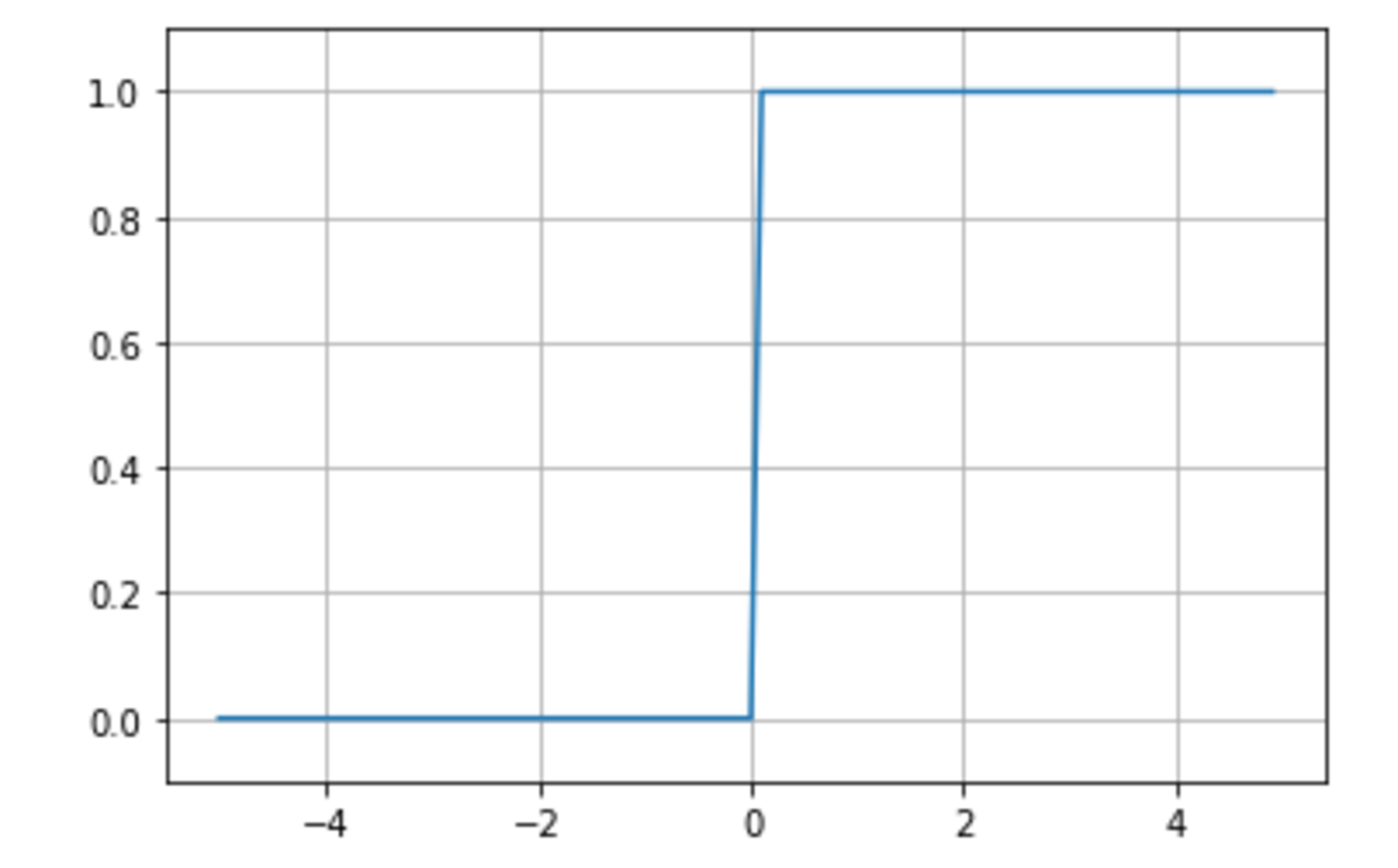ステップ関数
■課題
- 0-1間を表現できず、線形分離可能なものでしか学習できなかった。
シグモイド関数
0 ~ 1の間を緩やかに変化する関数で、ステップ関数ではON/OFFしかない状態に対し、信号の強弱を伝えられるようになった。
\begin{align} f(x) &= \frac{1}{1 + \exp(-x)} \end{align}
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.arange(-10.0, 10.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.grid()
plt.show()
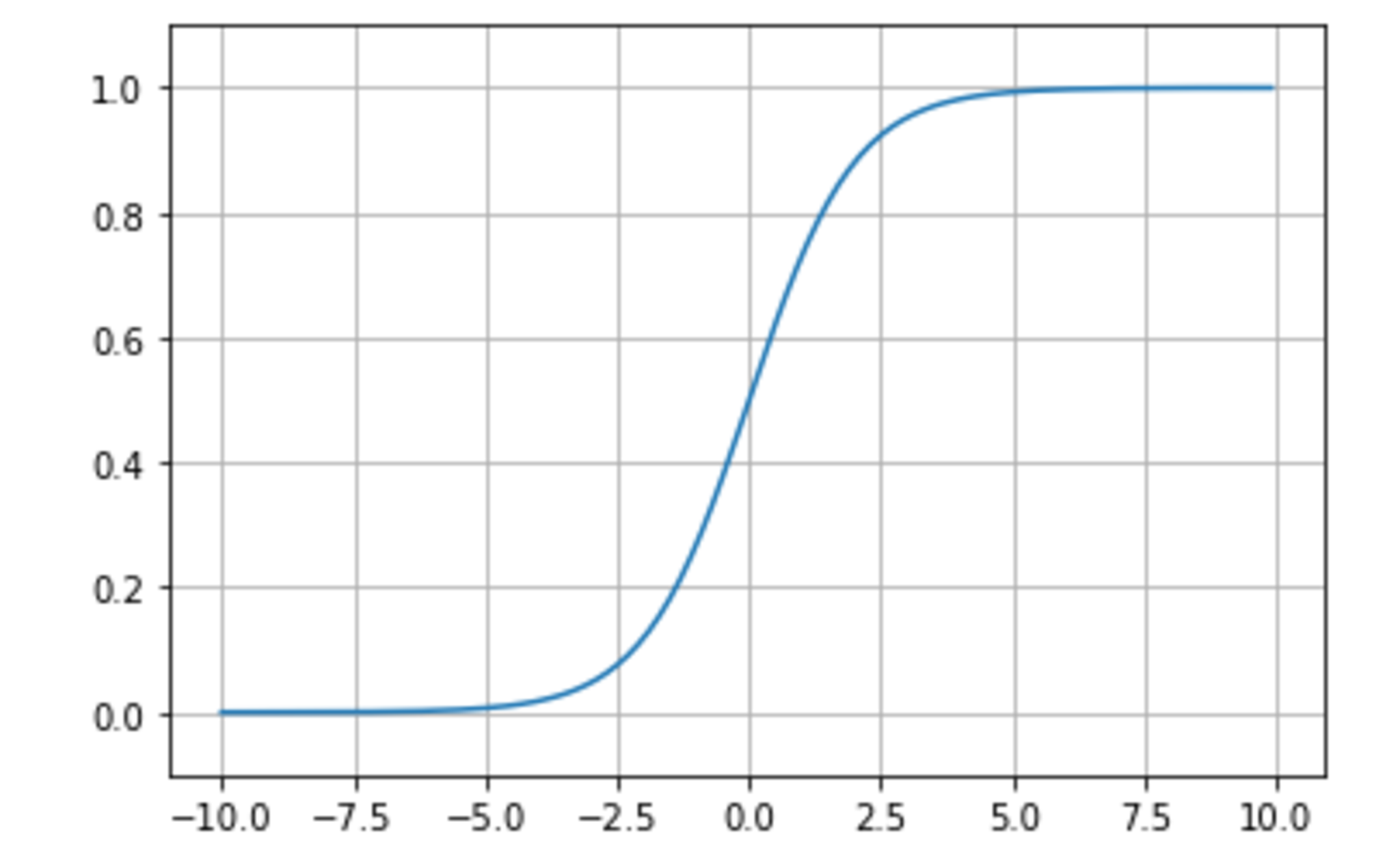シグモイド関数
■課題
- 大きな値では出力の変化が微小なため、勾配消失問題を引き起こす事があった。
ReRU関数
今最も使われている活性化関数勾配消失問題の回避とスパース化に貢献することで良い成果をもたらしている。
\begin{align} f(x) &= \begin{cases} x & (x > 0) \\ 0 & (x \le 0) \end{cases} \end{align}
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.grid()
plt.show()
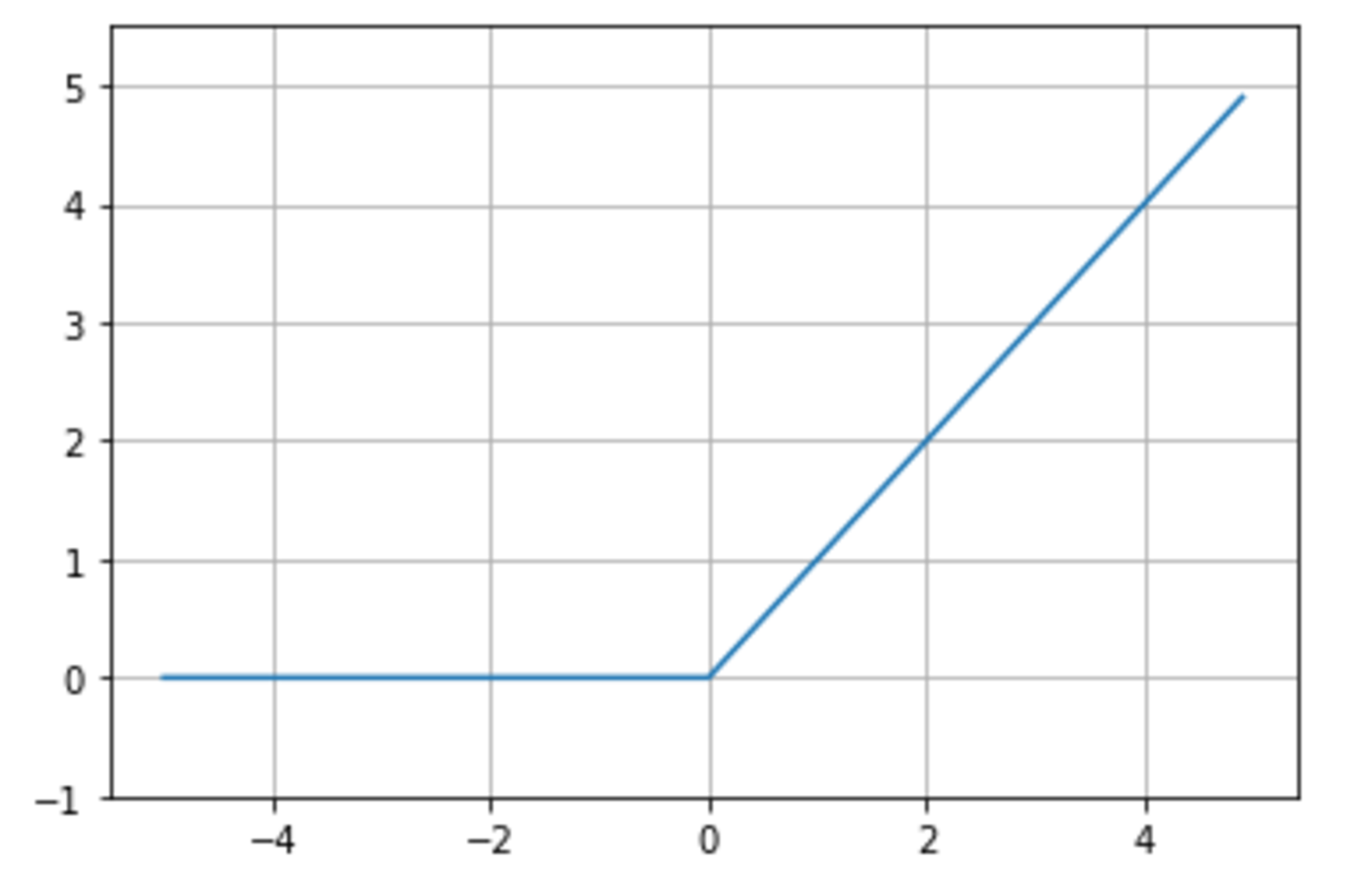ReRU関数
Section3：出力層
出力層の役割
人間が欲しい最終的なデータである結果を出力する。
誤差関数
実際にニューラルネットワークの学習においては、入力データと訓練データ（正解値）を用意する。
そして出力層の結果と目的変数の正解値を比較し、どの程度誤差があるのかを定量的に評価するために用いる関数を誤差関数という。
よく用いられるのは二乗誤差と交差エントロピーである。
まずは二乗誤差は以下で定義される式である。
\begin{align} E_{n}(w) = \frac{1}{2}\sum_{i=1}^{I} (y_{i} − d_{i})^2 = \frac{1}{2} \|y−d\|^2 \end{align}
この式は単に引き算をしたうえで、2乗をしている。
それは各ラベルでの誤差が正負両方の値が発生した場合、打ち消し合いしてしまうと、誤差が正しく評価さなくなるため。
また、$1/2$倍をしている理由としては、微分したときに2乗の2が前に出るため、計算式が全体的に綺麗になるため(本質的な理由ではなく、形式的な理由によるもの)。
交差エントロピーは以下で定義される式である。
\begin{align} E_{n}(w) = -\sum_{i=1}^{I} d_{i} \log y_{i} \end{align}
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
■確認テスト
交差エントロピーの
① $E_{n}(w)$、② $-\sum_{i=1}^{I} d_{i} \log y_{i}$ に該当するコードを示せ。
〇解答
①、②
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
なお、分母は極限に関連する調整をおこなっている項であり、②の本質は分子が担っている。
学習サイクルあたりの誤差は以下の通り定義される。
\begin{align}
E(w)
= -\sum_{n=1}^{N} E_{n}(w)
\end{align}
出力層の活性化関数
出力層と中間層で利用される活性化関数が異なる。
- 値の強弱
- 中間層︓しきい値の前後で信号の強弱を調整する。
- 出力層︓信号の大きさ（比率）はそのままに変換する。
- 確率出力
- 分類問題の場合、出力層の出力は 0 ~ 1 に限定、かつ総和が1になるようにする必要がある。
出力層の種類は以下の通り。
| 回帰 | 二値分類 | 多クラス分類 | |
|---|---|---|---|
| 活性化関数 | 恒等写像 | シグモイド関数 | ソフトマックス関数 |
| 誤差関数 | 二乗誤差 | 交差エントロピー | 交差エントロピー |
なお、ソフトマックス関数は以下で定義される関数。
\begin{align}
f(i, u)
= \frac{\exp(u_{i})}{\sum_{k=1}^{K} \exp(u_{k})}
\end{align}
# ソフトマックス関数
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
■確認テスト
ソフトマックス関数の
① $f(i,u)$、② $\exp(u_i)$、③ $\sum_{k=1}^K \exp(u_k)$ に該当するコードを示せ。
〇解答
①
return y.T
②
np.exp(x)
③
np.sum(np.exp(x),axis=0)
Section4：勾配降下法
深層学習の目的は、学習を通して誤差を最小にするネットワークを作成することであるが、
その誤差を最小にするために、パラメータを最適化する具体的なアルゴリズムが勾配降下法である。
勾配降下法とその種類
勾配降下法
通常の勾配降下法は以下の通り、全サンプルの平均誤差を取る。
\begin{align} w^{(t+1)} &= w^{(t)} - \epsilon \nabla E \tag{3-1} \\ \nabla E &= \frac{\partial E}{\partial w} = \left[\frac{\partial E}{\partial w_{1}}, \cdots \frac{\partial E}{\partial w_{M}} \right] \tag{3-2} \end{align}
この$\epsilon$のことを学習率という。
- 学習率の値によって学習の効率が大きく異なる
- 学習率が大きすぎた場合、最小値にいつまでもたどり着かず発散してしまう。
- 学習率が小さい場合、収束するまでに時間がかかってしまう。
■確認テスト
式(3-1), (3-2)のソースを探せ。
〇解答
式(3-1)
network[key] -= learning_rate* grad[key]
式(3-2)
grad = backward(x, d, z1, y)
確率的勾配降下法
確率的勾配降下法(SGD)は以下の通り、ランダムに抽出したサンプルの誤差を取る。
\begin{align} w^{(t+1)} = w^{(t)} - \epsilon \nabla E_{n} \end{align}
確率的勾配降下法のメリットは以下の通り。
- データが冗⻑な場合の計算コストの軽減
- 望まない局所極小解に収束するリスクの軽減
- オンライン学習ができる
■確認テスト
オンライン学習とはなにか、2行でまとめよ。
〇解答
学習データを得たら、その都度そのデータを用いてパラメータを更新し、学習を行う方法のことを指す。
一方、バッチ学習では、学習データをすべての一度に使ってパラメータの更新を行う。
ミニバッチ勾配降下法
ミニバッチ勾配降下法は以下の通り、ランダムに分割したデータの集合(ミニバッチ)$D_{t}$に属するサンプルの平均誤差を取る。
\begin{align} w^{(t+1)} &= w^{(t)} - \epsilon \nabla E_{t} \\ E_{t} &= \frac{1}{N_{t}} \sum_{n \in D_{t}} E_{n} \\ N_{t} &= |D_{t}| \end{align}
ミニバッチ勾配降下法のメリットは以下の通り。
- 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる。
- CPUを利用したスレッド並列化やGPUを利用したSIMD並列化が可能になる。
誤差勾配の数値微分による計算
\begin{align} \nabla E &= \frac{\partial E}{\partial w} = \left[\frac{\partial E}{\partial w_{1}}, \cdots \frac{\partial E}{\partial w_{M}} \right] \end{align}
数値計算だと、発散する可能性があるため、以下のように計算することが一般的。
\begin{align} \frac{\partial E}{\partial w_m} &= \lim_{h \to 0} \frac{E(w_{m} + h) - E(w_{m} - h)}{2h} \end{align}
勾配降下法の学習率の決定、収束性向上のためのアルゴリズム
複数の論文が公開され、よく利用されている。
- Momentum
- AdaGrad
- Adadelta
- Adam
Section5：誤差逆伝播法
誤差逆伝播法とは、算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播させる方法。
数値微分で扱った、各パラメータ$w_{m}$をそれぞれ$E(w_{m} + h), E(w_{m} - h)$を計算するために、順伝播の計算を繰り返し行うことは負荷が大きい。
計算結果（=誤差）から微分を逆算することで、不要な再帰的計算を避けて微分を算出できることができることから、最小限の計算で各パラメータでの微分値を解析的に計算できる。
■確認テスト
誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
既に行った計算結果を保持しているソースコードを抽出せよ。
〇解答
# 出力層でのデルタ
delta2 = functions.d_sigmoid_with_loss(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
■確認テスト
$\displaystyle \frac{\partial E}{\partial y}$
delta2 = functions.d_mean_squared_error(d, y)
$\displaystyle \frac{\partial E}{\partial y} \frac{\partial y}{\partial u}$および$\displaystyle \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w_{ji}^{(2)}}$に該当するソースコードを探せ。
※ここで用いられるz1は以下のコードで生成される
z1, y = forward(network, x)
〇解答
$\displaystyle \frac{\partial E}{\partial y} \frac{\partial y}{\partial u}$
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
$\displaystyle \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w_{ji}^{(2)}}$
grad['W2'] = np.dot(z1.T, delta2)
実装演習
確率的勾配降下法を誤差逆伝播法で実装する。
import numpy as np
from common import functions
import matplotlib.pyplot as plt
def print_vec(text, vec):
print("*** " + text + " ***")
print(vec)
#print("shape: " + str(x.shape))
print("")
# サンプルとする関数
# yの値を予想するAI
def f(x):
y = 3 * x[0] + 2 * x[1]
return y
# 初期設定
def init_network():
# print("##### ネットワークの初期化 #####")
network = {}
nodesNum = 10
network['W1'] = np.random.randn(2, nodesNum)
network['W2'] = np.random.randn(nodesNum)
network['b1'] = np.random.randn(nodesNum)
network['b2'] = np.random.randn()
# print_vec("重み1", network['W1'])
# print_vec("重み2", network['W2'])
# print_vec("バイアス1", network['b1'])
# print_vec("バイアス2", network['b2'])
return network
# 順伝播
def forward(network, x):
# print("##### 順伝播開始 #####")
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
u1 = np.dot(x, W1) + b1
z1 = functions.relu(u1)
## 試してみよう
#z1 = functions.sigmoid(u1)
u2 = np.dot(z1, W2) + b2
y = u2
# print_vec("総入力1", u1)
# print_vec("中間層出力1", z1)
# print_vec("総入力2", u2)
# print_vec("出力1", y)
# print("出力合計: " + str(np.sum(y)))
return z1, y
# 誤差逆伝播
def backward(x, d, z1, y):
# print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
#delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
## 試してみよう
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
delta1 = delta1[np.newaxis, :]
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
# print_vec("偏微分_重み1", grad["W1"])
# print_vec("偏微分_重み2", grad["W2"])
# print_vec("偏微分_バイアス1", grad["b1"])
# print_vec("偏微分_バイアス2", grad["b2"])
return grad
# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]
for i in range(data_sets_size):
data_sets[i] = {}
# ランダムな値を設定
data_sets[i]['x'] = np.random.rand(2)
## 試してみよう_入力値の設定
# data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
# 目標出力を設定
data_sets[i]['d'] = f(data_sets[i]['x'])
losses = []
# 学習率
learning_rate = 0.07
# 抽出数
epoch = 1000
# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)
# 勾配降下の繰り返し
for dataset in random_datasets:
x, d = dataset['x'], dataset['d']
z1, y = forward(network, x)
grad = backward(x, d, z1, y)
# パラメータに勾配適用
for key in ('W1', 'W2', 'b1', 'b2'):
network[key] -= learning_rate * grad[key]
# 誤差
loss = functions.mean_squared_error(d, y)
losses.append(loss)
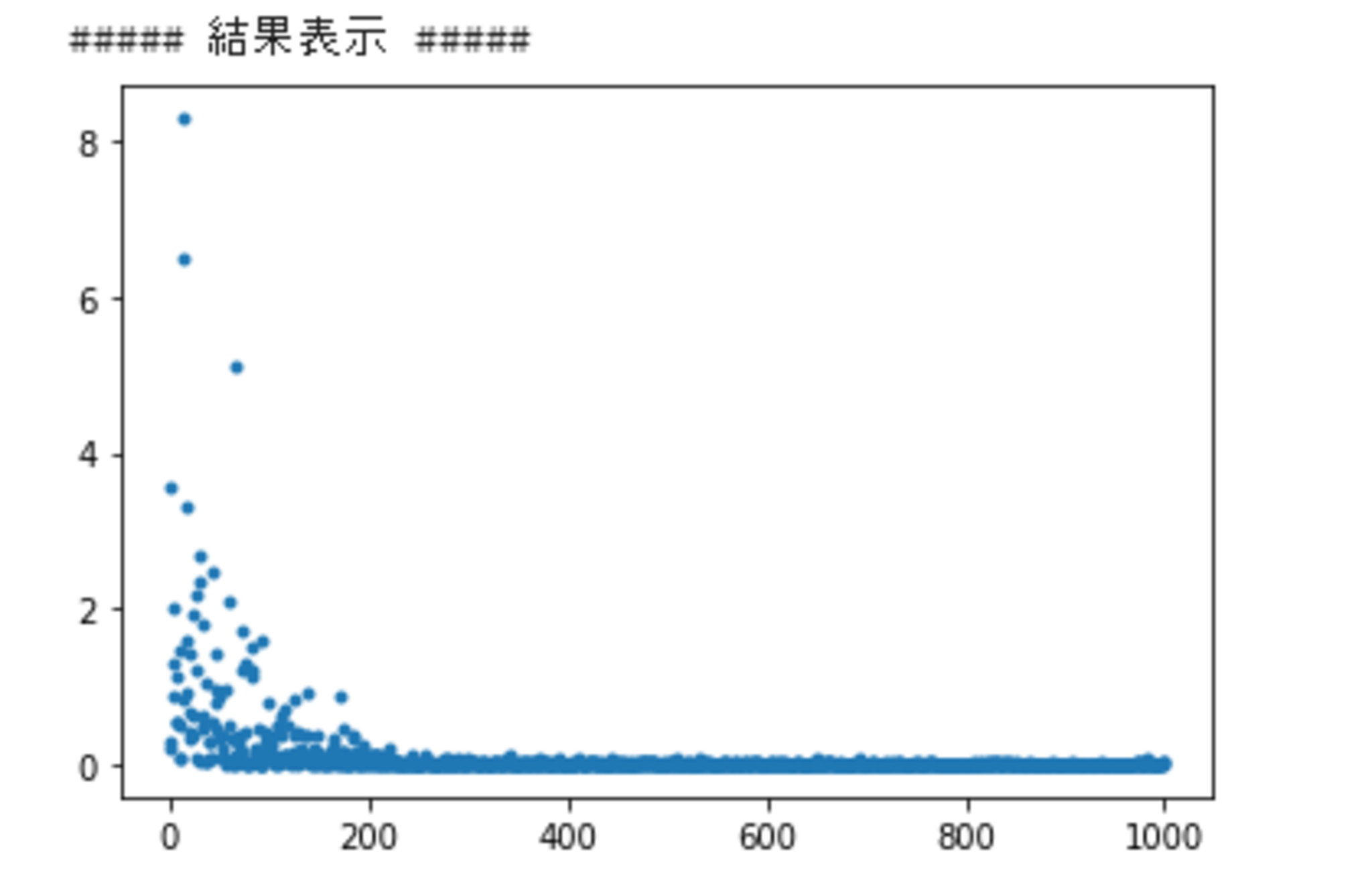
print("##### 結果表示 #####")
lists = range(epoch)
plt.plot(lists, losses, '.')
# グラフの表示
plt.show()
