[ラビットチャレンジ] 深層学習day3 レポート
はじめに
本稿は、E資格の受験資格の取得を目的としたラビットチャレンジの受講に伴うレポート記事である。
Section1:再帰型ニューラルネットワークの概念
概要
再帰型ニューラルネットワーク(RNN)とは、時系列データに対応可能な、ニューラルネットワークである。
時系列データとは、時間的順序を追って一定間隔ごとに観察され,しかも相互に統計的依存関係が認められるようなデータの系列を指す。具体例としては、音声データ・テキストデータが挙げられる。
時系列データを扱うために、初期の状態と過去の時間$t-1$の状態を保持し、その保持した状態から次の時間$t$の情報を再帰的に求めることができる再帰構造が必要となる。
全体図
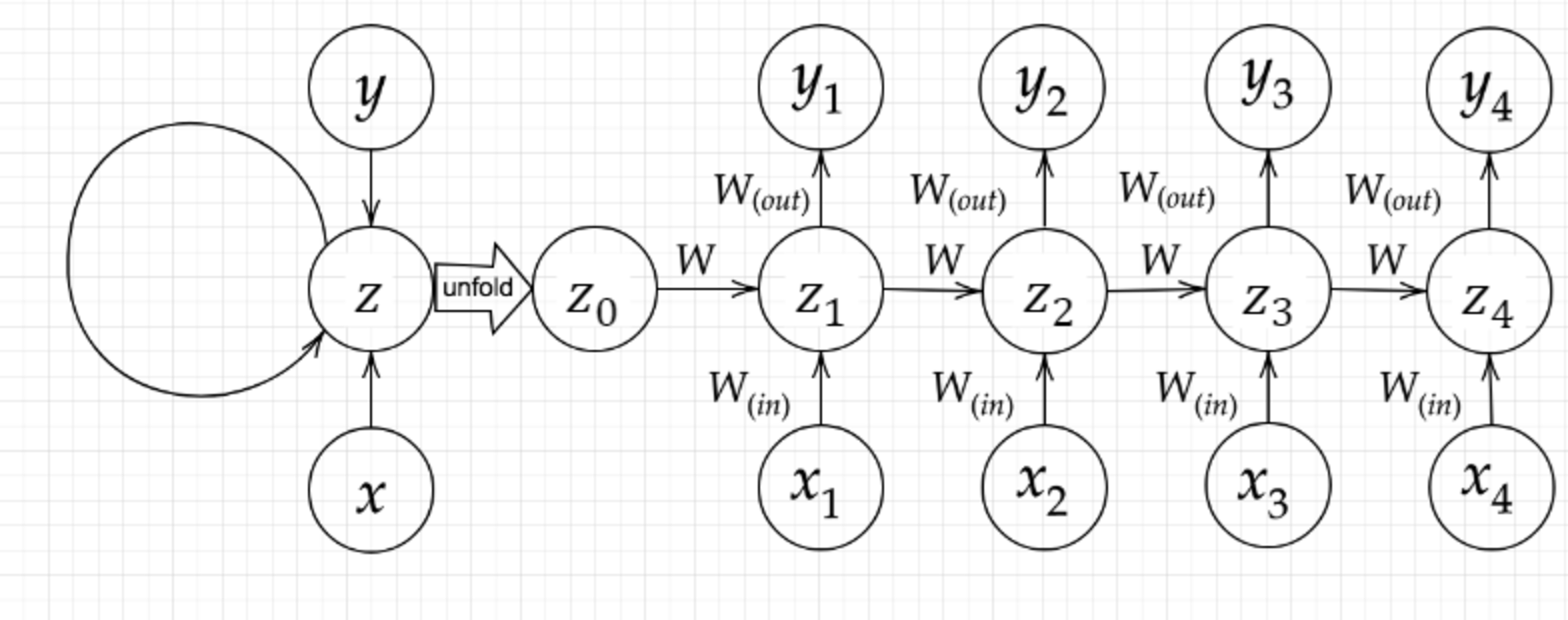 RNNの全体図
RNNの全体図
■確認テスト
RNNのネットワークには大きくわけて3つの重みがある。1つは入力から現在の中間層を定義する際にかけられる重み($W_{(in)}$)、1つは中間層から出力を定義する際にかけられる重み($W_{(out)}$)である。
残り1つの重みについて説明せよ。
〇解答
前の中間層から現在の中間層を定義する際にかけられる重み$W$が該当する。
RNNにおいて、この$W$が再帰のもととなることから、一番大事であり、RNNという呼び方もこれがあるからである。
数学的記述と実装
\begin{align} u^t &= W_{(in)} x^t + W z^{t-1} + b \tag{1-1}\\ z^t &= f(u^t) = f(W_{(in)} x^t + W z^{t-1} + b) \tag{1-2}\\ v^t &= W_{(out)} z^t + c \tag{1-3}\\ y^t &= f(v^t) = f(W_{(out)} z^t + c) \tag{1-4} \end{align}
式(1-1)の実装
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
式(1-2)の実装
z[:,t+1] = functions.sigmoid(u[:,t+1])
式(1-3)の実装
np.dot(z[:,t+1].reshape(1, -1), W_out)
式(1-4)の実装
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))
BPTT
BPTTとは、RNNにおいてのパラメータ調整方法のひとつで、誤差逆伝播の一種である。
数学的に記述すると、以下のようになる。
\begin{align} \frac{\partial E}{\partial W_{(in)}} &= \frac{\partial E}{\partial u^t} \left[\frac{\partial u^t}{\partial W_{(in)}}\right]^T = \delta^t [x^t]^T \\ \frac{\partial E}{\partial W_{(out)}} &= \frac{\partial E}{\partial v^t} \left[\frac{\partial v^t}{\partial W_{(out)}}\right]^T = \delta^{out, t} [z^t]^T \\ \frac{\partial E}{\partial W} &= \frac{\partial E}{\partial u^t} \left[\frac{\partial u^t}{\partial W}\right]^T = \delta^{t} [z^{t-1}]^T \\ \frac{\partial E}{\partial b} &= \frac{\partial E}{\partial u^t} \frac{\partial u^t}{\partial b} = \delta^{t} \\ \frac{\partial E}{\partial c} &= \frac{\partial E}{\partial v^t} \frac{\partial v^t}{\partial c} = \delta^{out, t} \\ u^t &= W_{(in)} x^t + W z^{t-1} + b \\ z^t &= f(u^t) = f(W_{(in)} x^t + W z^{t-1} + b) \\ v^t &= W_{(out)} z^t + c \\ y^t &= f(v^t) = f(W_{(out)} z^t + c) \end{align}
実装演習
import numpy as np
from common import functions
import matplotlib.pyplot as plt
# def d_tanh(x):
# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
input_layer_size = 2
hidden_layer_size = 16
output_layer_size = 1
weight_init_std = 1
learning_rate = 0.1
iters_num = 10000
plot_interval = 100
# ウェイト初期化 (バイアスは簡単のため省略)
W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std * np.random.randn(hidden_layer_size, hidden_layer_size)
# Xavier
# He
# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)
u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))
delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))
all_losses = []
for i in range(iters_num):
# A, B初期化 (a + b = d)
a_int = np.random.randint(largest_number/2)
a_bin = binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2)
b_bin = binary[b_int] # binary encoding
# 正解データ
d_int = a_int + b_int
d_bin = binary[d_int]
# 出力バイナリ
out_bin = np.zeros_like(d_bin)
# 時系列全体の誤差
all_loss = 0
# 時系列ループ
for t in range(binary_dim):
# 入力値
X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
# 時刻tにおける正解データ
dd = np.array([d_bin[binary_dim - t - 1]])
u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
z[:,t+1] = functions.sigmoid(u[:,t+1])
y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))
#誤差
loss = functions.mean_squared_error(dd, y[:,t])
delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])
all_loss += loss
out_bin[binary_dim - t - 1] = np.round(y[:,t])
for t in range(binary_dim)[::-1]:
X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)
delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])
# 勾配更新
W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
# 勾配適用
W_in -= learning_rate * W_in_grad
W_out -= learning_rate * W_out_grad
W -= learning_rate * W_grad
W_in_grad *= 0
W_out_grad *= 0
W_grad *= 0
if(i % plot_interval == 0):
all_losses.append(all_loss)
print("iters:" + str(i))
print("Loss:" + str(all_loss))
print("Pred:" + str(out_bin))
print("True:" + str(d_bin))
out_int = 0
for index,x in enumerate(reversed(out_bin)):
out_int += x * pow(2, index)
print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
print("------------")
lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()
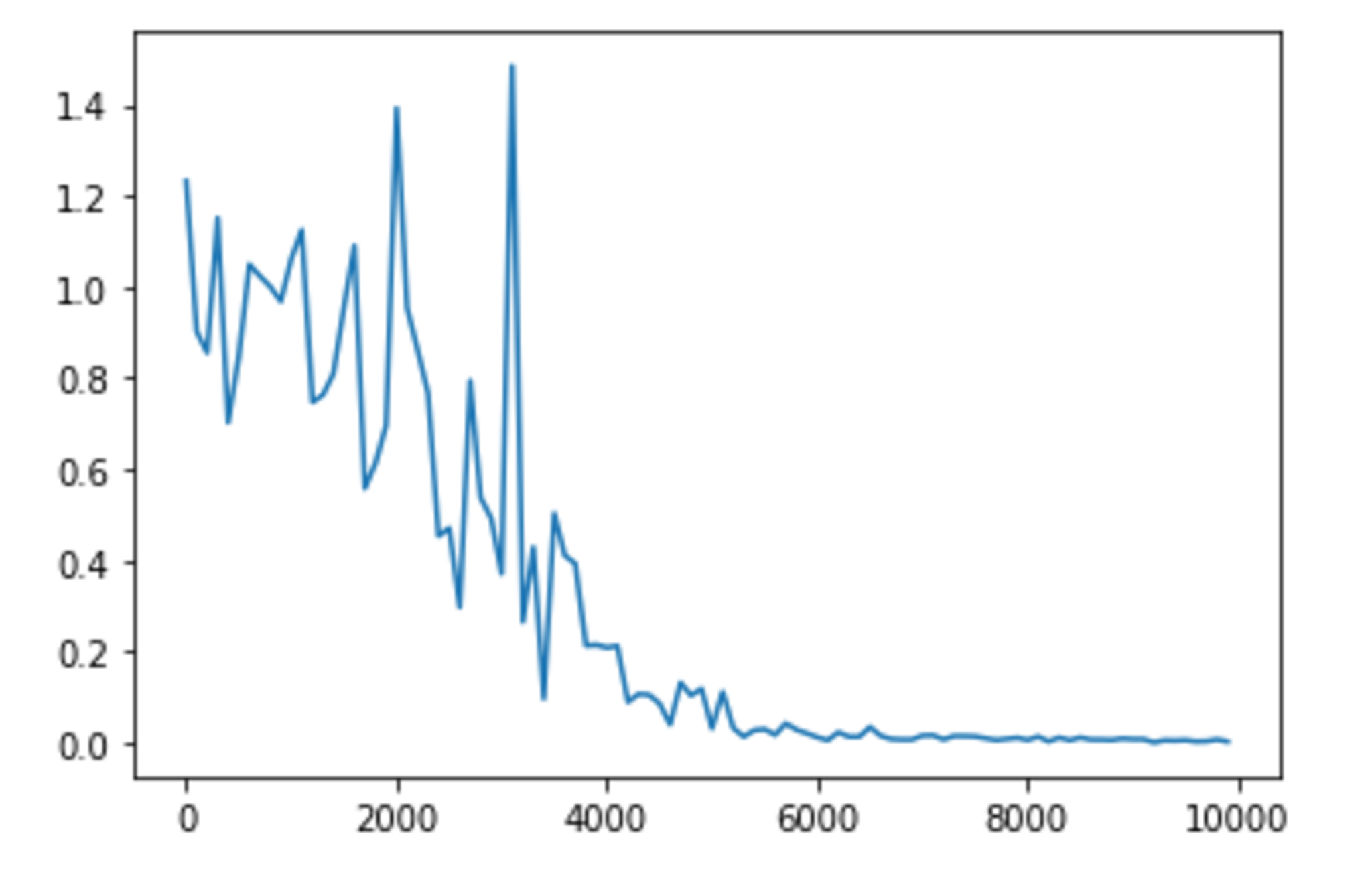
パラメータの変更
上記の結果に対してパラメータを変更し、状況がどのように変化するかを確認してみる。
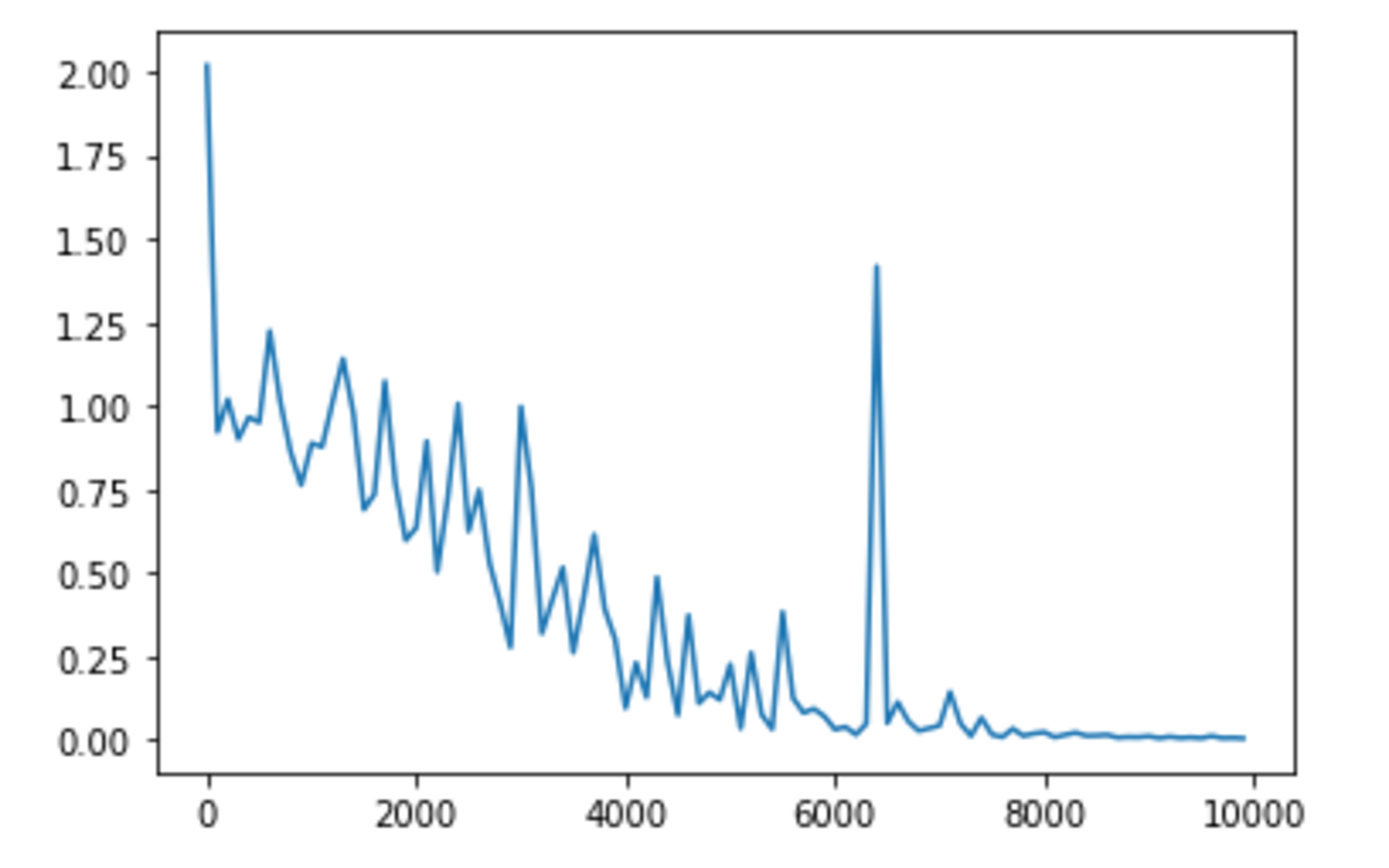 hidden_layer_size = 8 の場合
hidden_layer_size = 8 の場合
 hidden_layer_size = 16 の場合
hidden_layer_size = 16 の場合
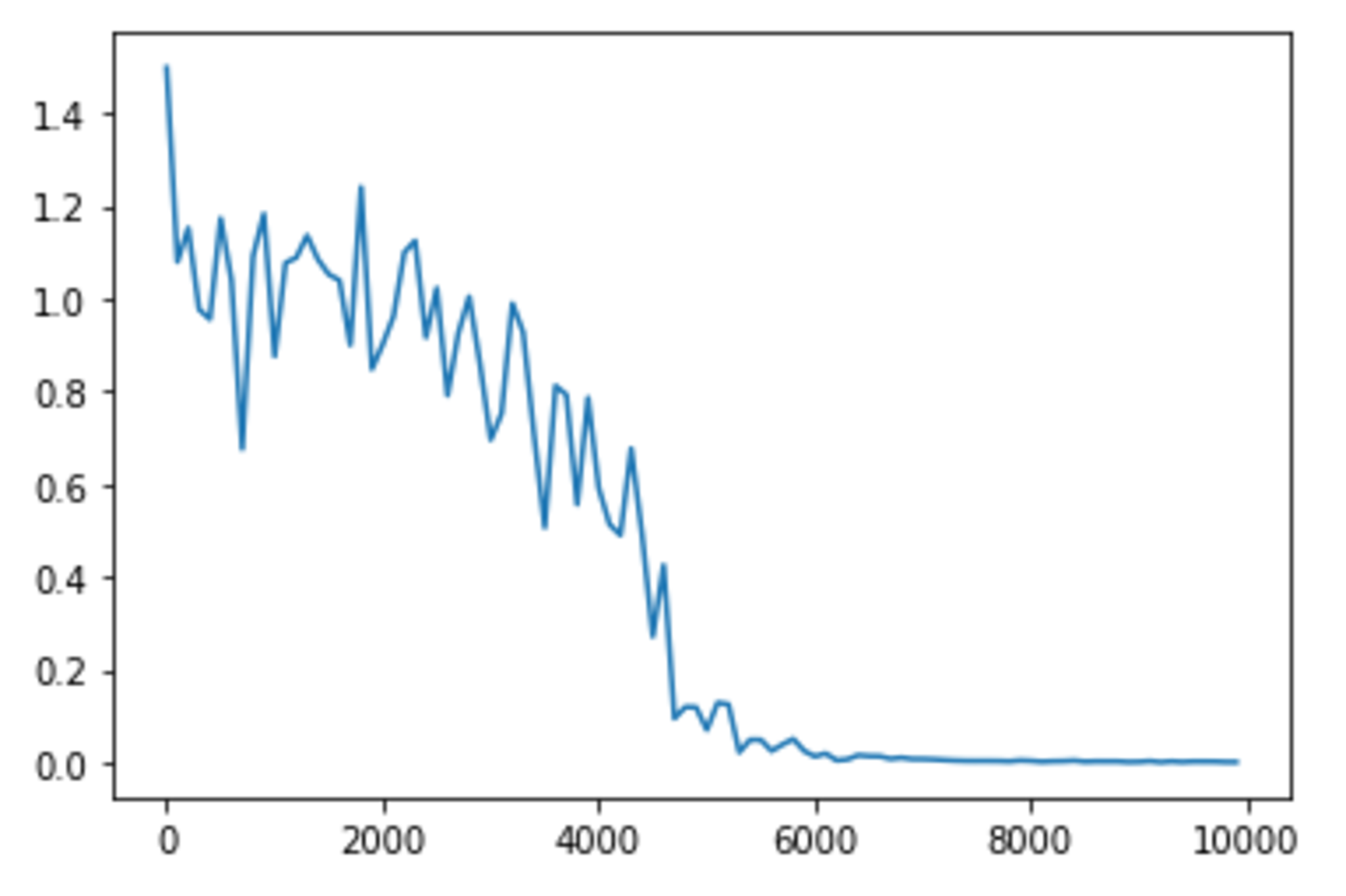 hidden_layer_size = 32 の場合
hidden_layer_size = 32 の場合
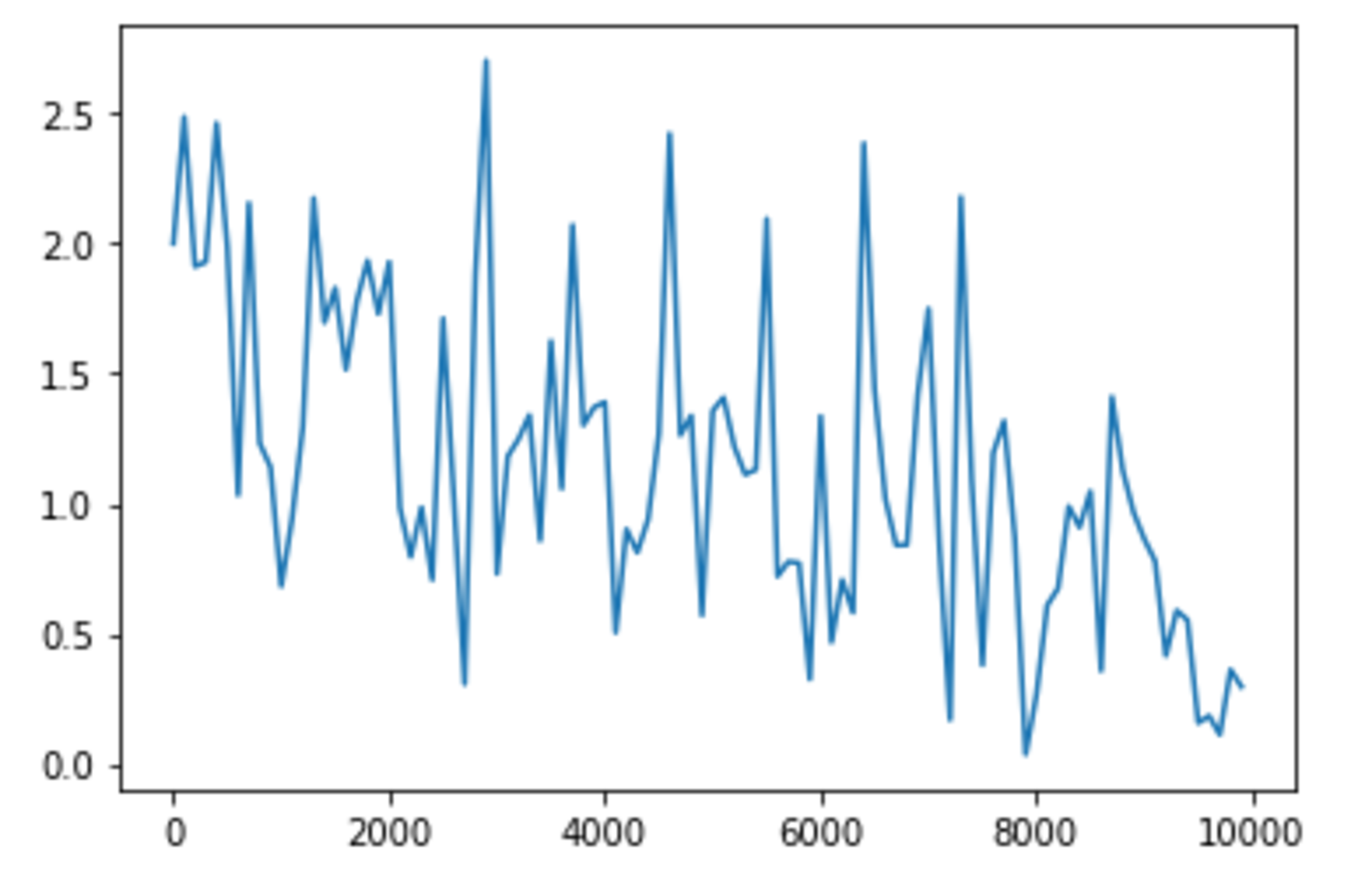 hidden_layer_size = 256 の場合
hidden_layer_size = 256 の場合
hidden_layer_sizeは16よりも32のほうが早いように見受けられる。一方で、8や256では、16よりも学習が遅くなっているように見受けられる。
weight_init_std
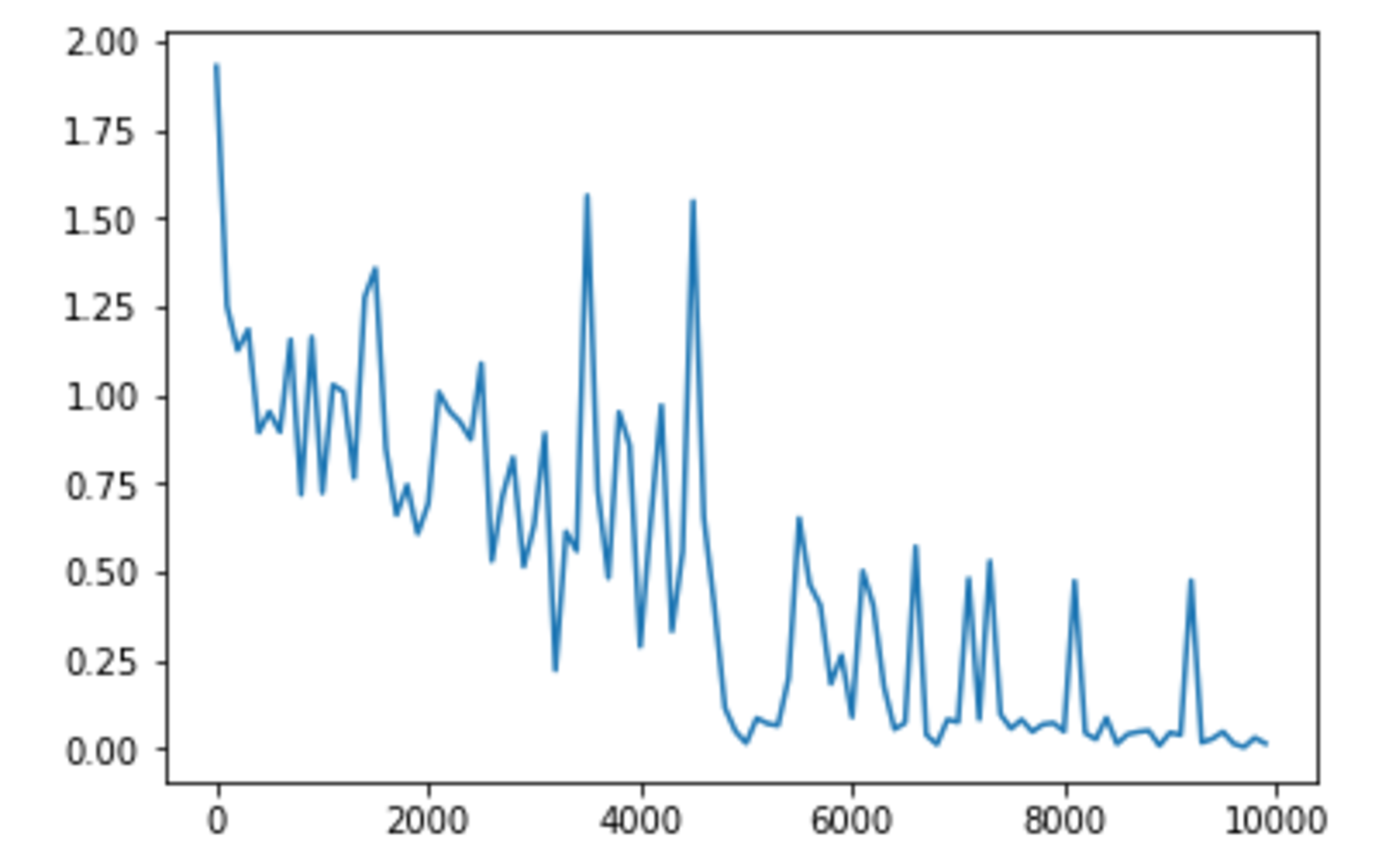 weight_init_std = 0.5 の場合
weight_init_std = 0.5 の場合
 weight_init_std = 1.0 の場合
weight_init_std = 1.0 の場合
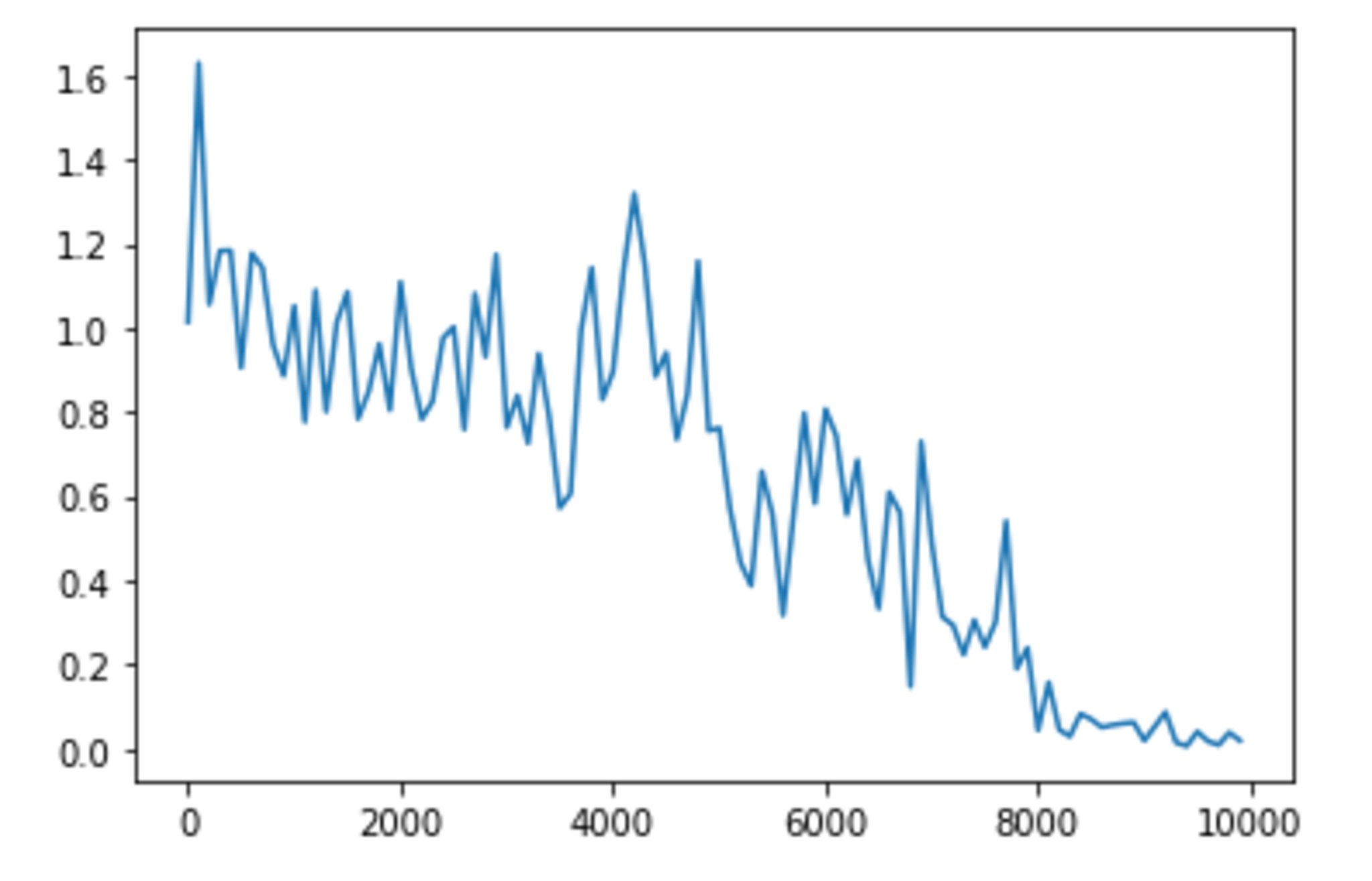 weight_init_std = 2.0 の場合
weight_init_std = 2.0 の場合
weight_init_stdは1.0が一番収束が早いように見受けられる。
learning_rate
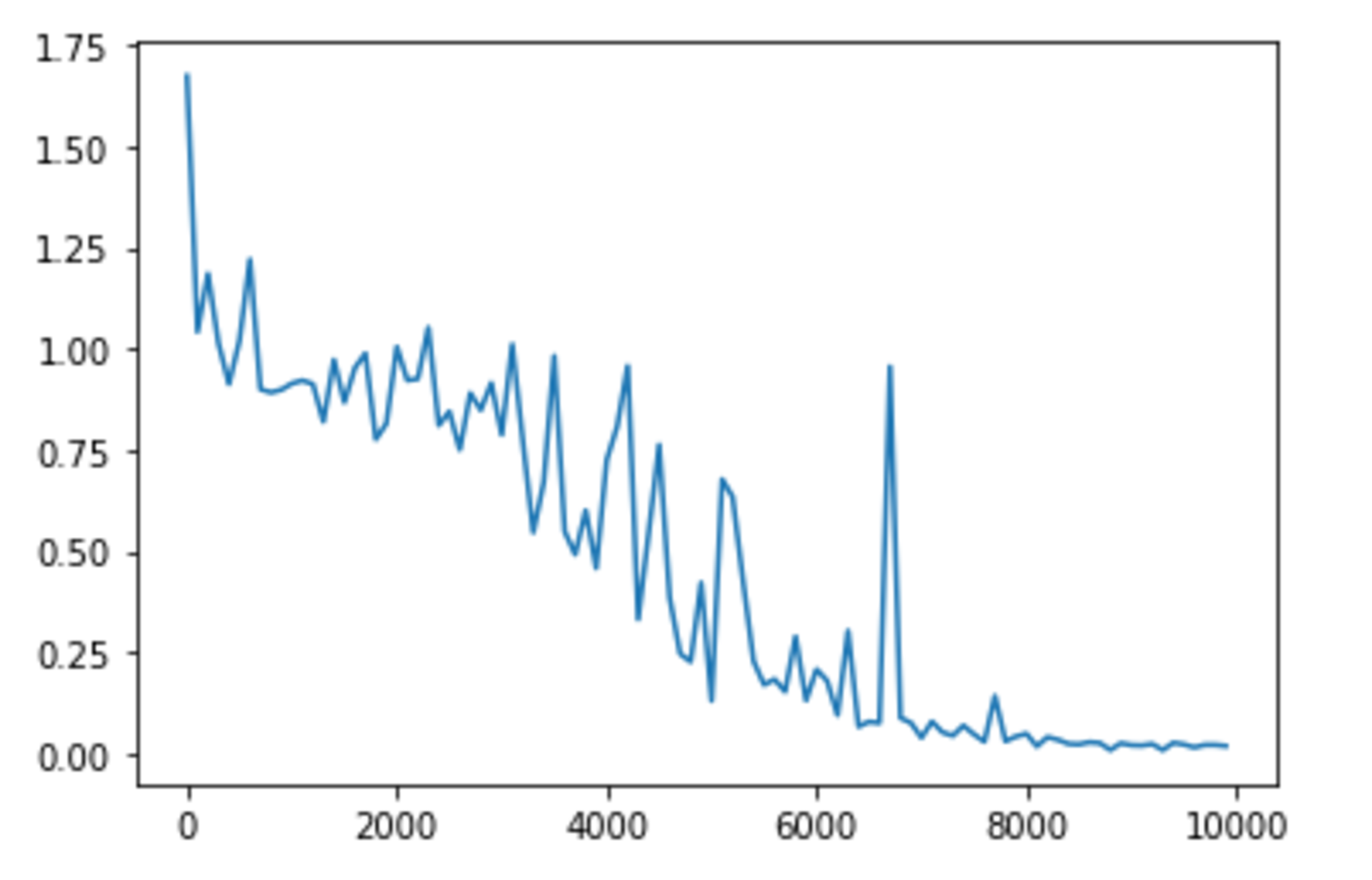 learning_rate = 0.05 の場合
learning_rate = 0.05 の場合
 learning_rate = 0.1 の場合
learning_rate = 0.1 の場合
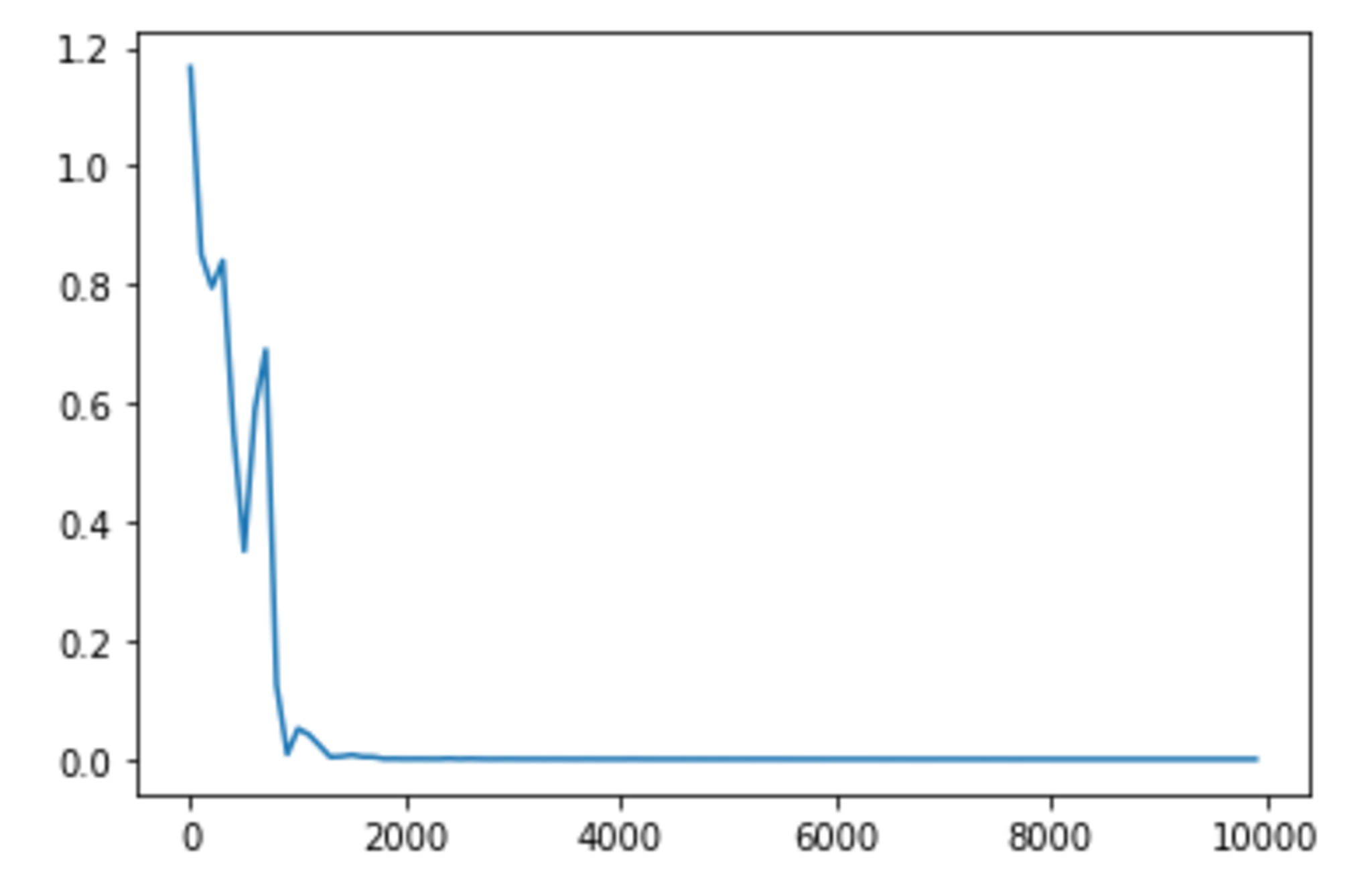 learning_rate = 1.0 の場合
learning_rate = 1.0 の場合
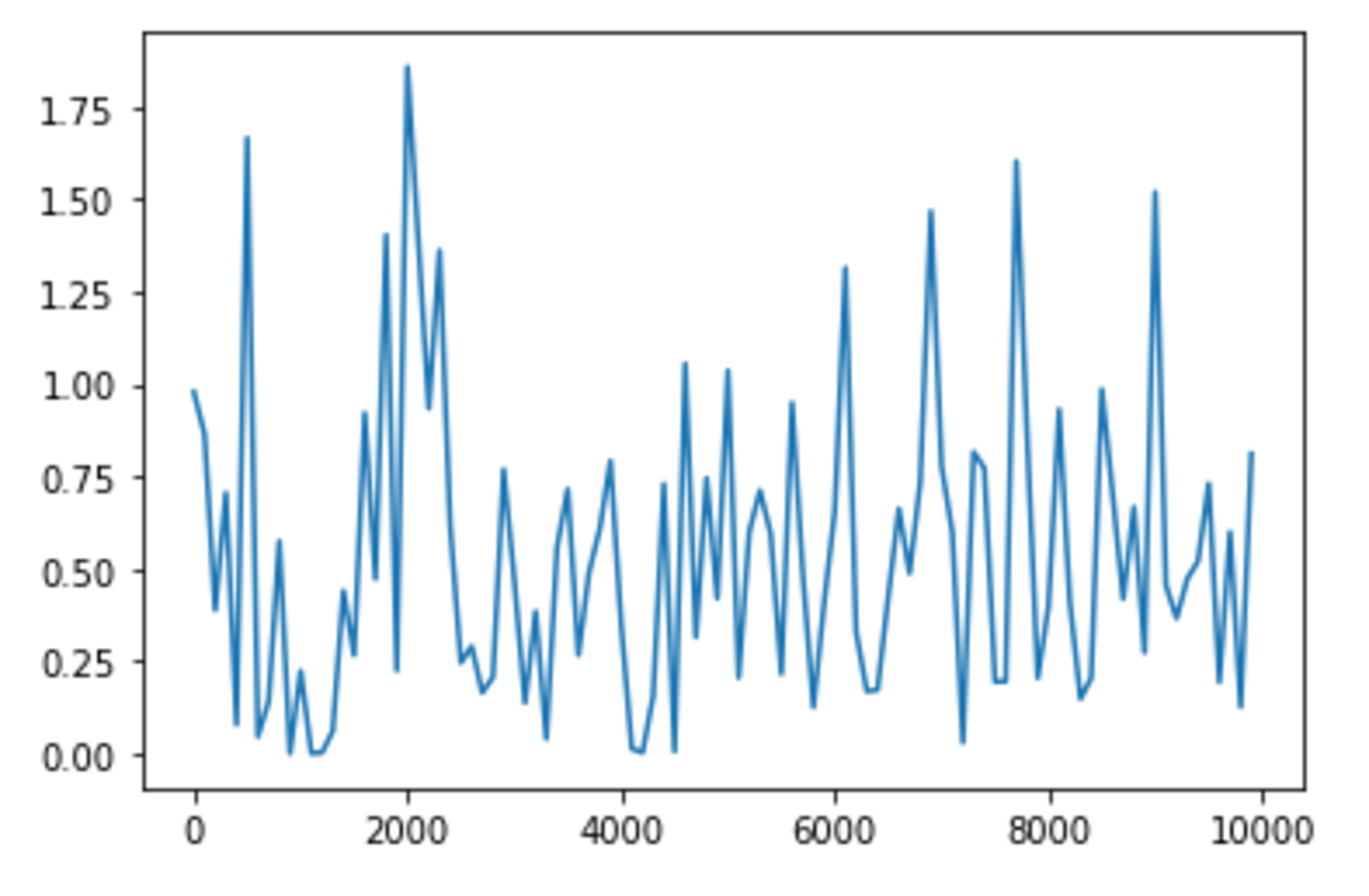 learning_rate = 4.0 の場合
learning_rate = 4.0 の場合
learning_rateは0.1から1.0に変更したとき、学習が早くなったように見受けられる。逆に0.01もしくは4に変更したとき、学習は遅くなったように見受けられる。
Section2:LSTM
RNNの課題として、時系列を遡れば遡るほど、勾配消失や勾配爆発が起きるため、長い時系列の学習が困難であることが挙げられる。
LSTM(Long Short-Term Memory)とは、学習の困難に対し、勾配消失の解決するアプローチではなく、構造自体を変えるアプローチにより解決したものである。
LSTMの定式化
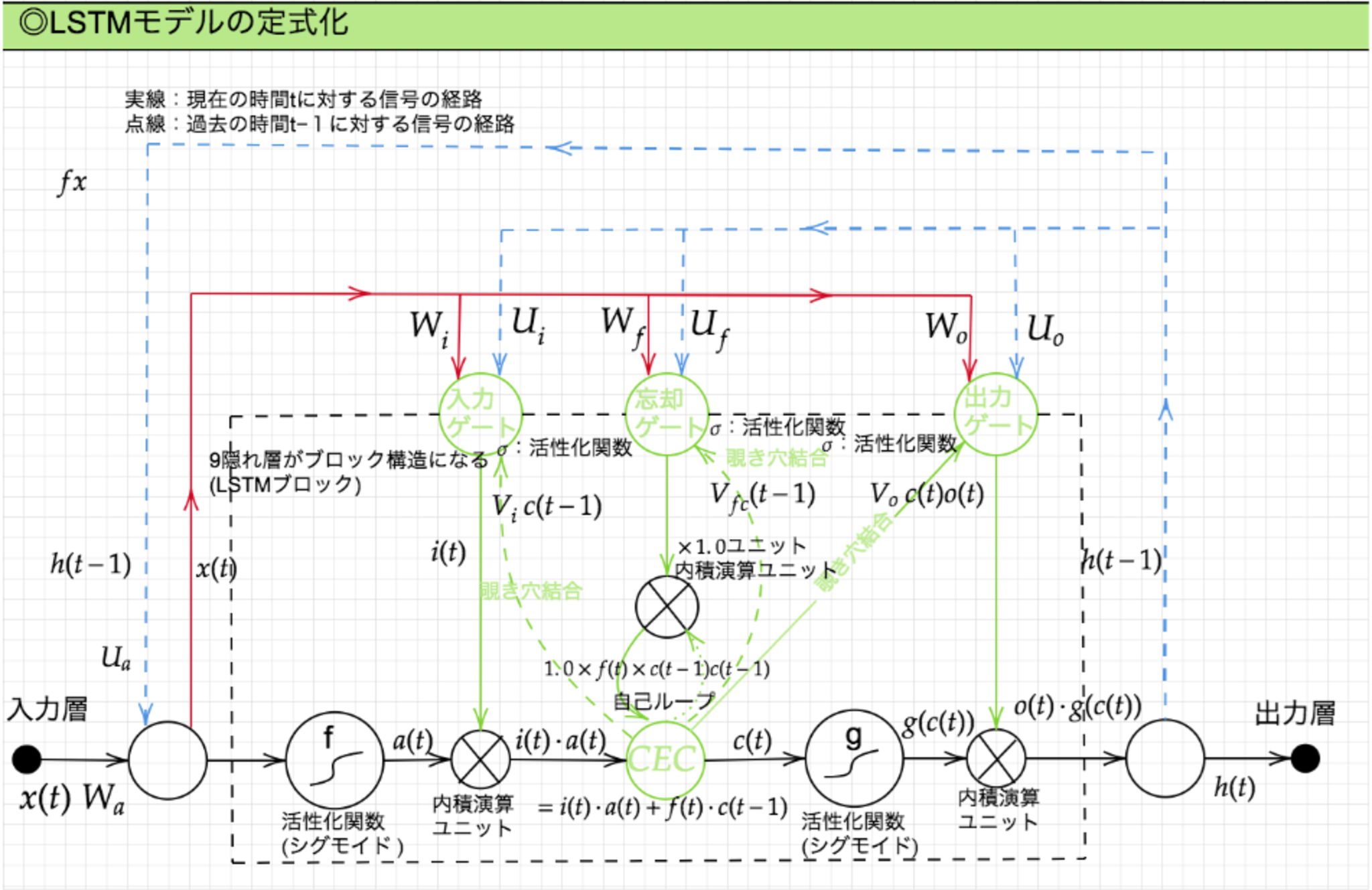
CEC
勾配消失及び勾配爆発の解決策として、勾配を$1$とした。
\begin{align} \delta^{t-z-1} &= \delta^{t-z} \{W f'(u^{t-z-1})\} = 1 \\ \frac{\partial E}{\partial c^{t-1}} &= \frac{\partial E}{\partial c^{t}} \frac{\partial c^{t}}{\partial c^{t-1}} \\ &= \frac{\partial E}{\partial c^{t}} \frac{\partial}{\partial c^{t-1}} (a^t - c^{t-1}) \\ &= \frac{\partial E}{\partial c^{t}} \end{align}
CECの課題として、入力データについて、時間依存度に関係なく重みが一律となることが挙げられる。
すなわち、ニューラルネットワークの学習特性がなくなってしまうことを意味する。
入力・出力ゲート
入力・出力ゲートを追加し、それぞれのゲートへの入力値の重みを、重み行列$W, U$で可変可能とする。
それによりCECの課題である学習特性のないことを解消することができる。
入力ゲート:1つ前の時間の出力をどの程度反映するかを調整する。
\begin{align} i(t) = \sigma(W_{i}(t) x(t) + U_i(t) h(t-1) + b_i) \end{align}出力ゲート:過去の出力を入力に反映させる。
\begin{align} o(t) = \sigma(W_o(t) x(t) + U_o(t) h(t-1) + b_o) \end{align}
忘却ゲート
現状のCECは、過去の情報が全て保管されており、過去の情報が要らなくなったであっても、削除することはできず、保管され続ける。
そこで、過去の情報が要らなくなったとき、そのタイミングで情報を忘却する機能として追加したものを忘却ゲートという。
\begin{align}
f(t) = \sigma(W_f(t) x(t) + U_f(t) h(t-1) + b_f)
\end{align}
■確認テスト
以下の文章をLSTMに入力し空欄に当てはまる単語を予測したいとする。
文中の「とても」という言葉は空欄の予測においてなくなっても影響を及ぼさないと考えられる。
このような場合、どのゲートが作用すると考えられるか。
「映画おもしろかったね。ところで、とてもお腹が空いたから何か____。」
〇解答
忘却ゲート
メモリーセル
\begin{align} \tilde{c}(t) &= \tanh(W_{\tilde{c}}(t) x(t) + U_{\tilde{c}}(t) h(t-1) + b_{\tilde{c}}) \\ c(t) &= i(t) \circ \tilde{c}(t) + f(t) \circ c(t-1) \end{align}
状態の更新
\begin{align} h(t) = o(t) \circ \tanh(c(t)) \end{align}
覗き穴結合
CECの保存されている過去の情報を、任意のタイミングで他のノードに伝播させたり、あるいは任意のタイミングで忘却させたい。
さらにCEC自身の値は、ゲート制御に影響を与えていない。
CEC自身の値に、重み行列を介して伝播可能にした構造のことを覗き穴結合という。
Section3:GRU
従来のLSTMでは、パラメータが多数存在していたため、計算負荷が大きかった。
しかし、GRUという構造を用いることで、パラメータを大幅に削減し、計算負荷を下げたにも関わらず、同等またはそれ以上の精度が得られるようになった。
GRUの全体像
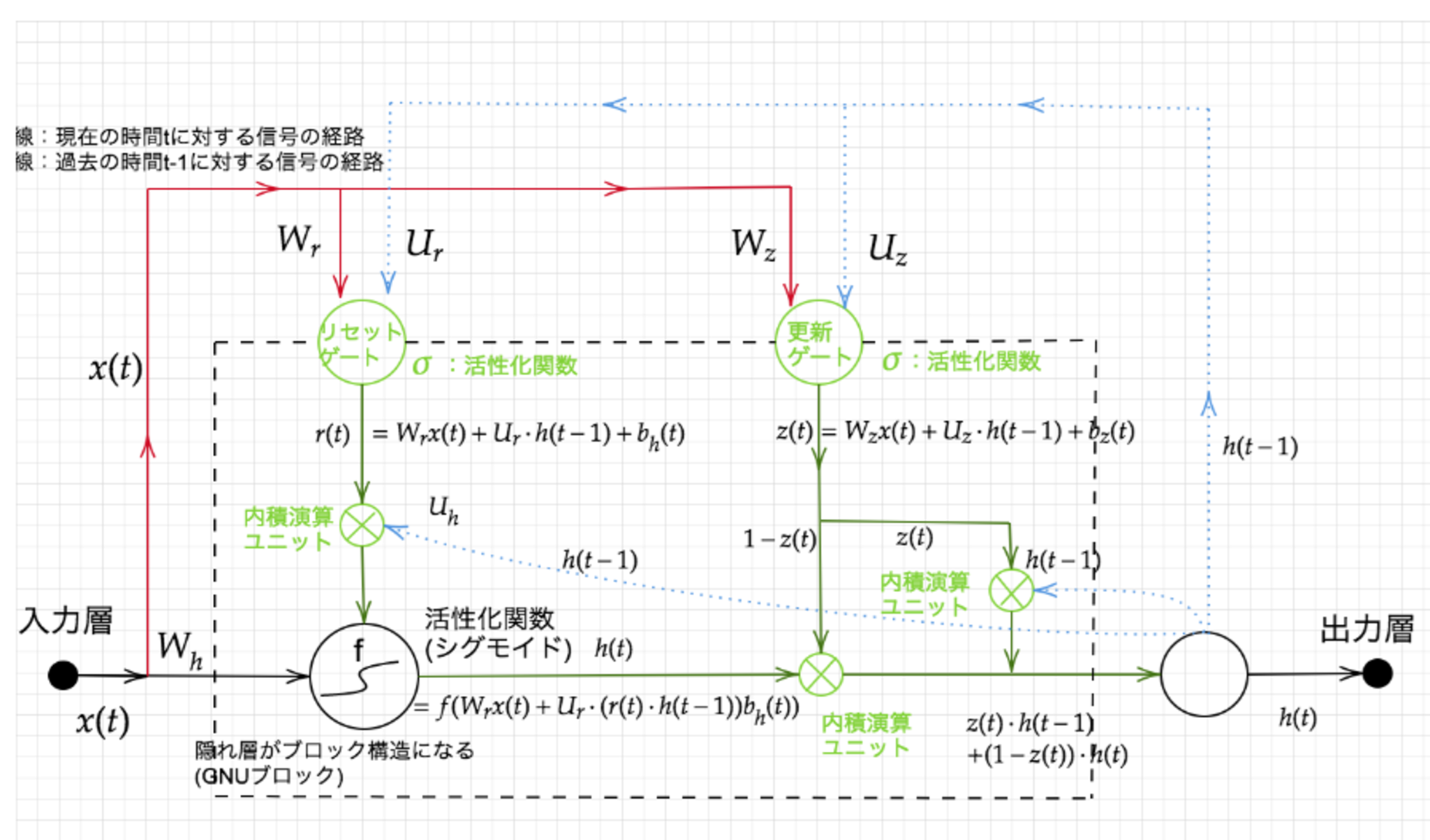 全体像
全体像
- 入力ゲートと忘却ゲートが統合され、更新ゲートとなっている。
- 記憶セルと出力ゲートがなく、値を0にリセットするリセットゲートがある。
■確認テスト
LSTMとCECが抱える課題について、それぞれ簡潔に述べよ。
〇解答
- LSTM -> パラメータ数が多く、計算負荷が高い。
- CEC -> ニューラルネットワークの学習特性がない。
■確認テスト
LSTMとGRUの違いを簡潔に述べよ。
〇解答
- LSTM -> パラメータが多数存在するため、計算負荷が大きい。
- GRU -> パラメータを大幅に削減し計算負荷を減らしたが、同等またはそれ以上の精度が望める。
Section4:双方向RNN
双方向RNNとは、過去の情報だけでなく、未来の情報を加味することで、精度を向上させるための
モデルのことを指す。
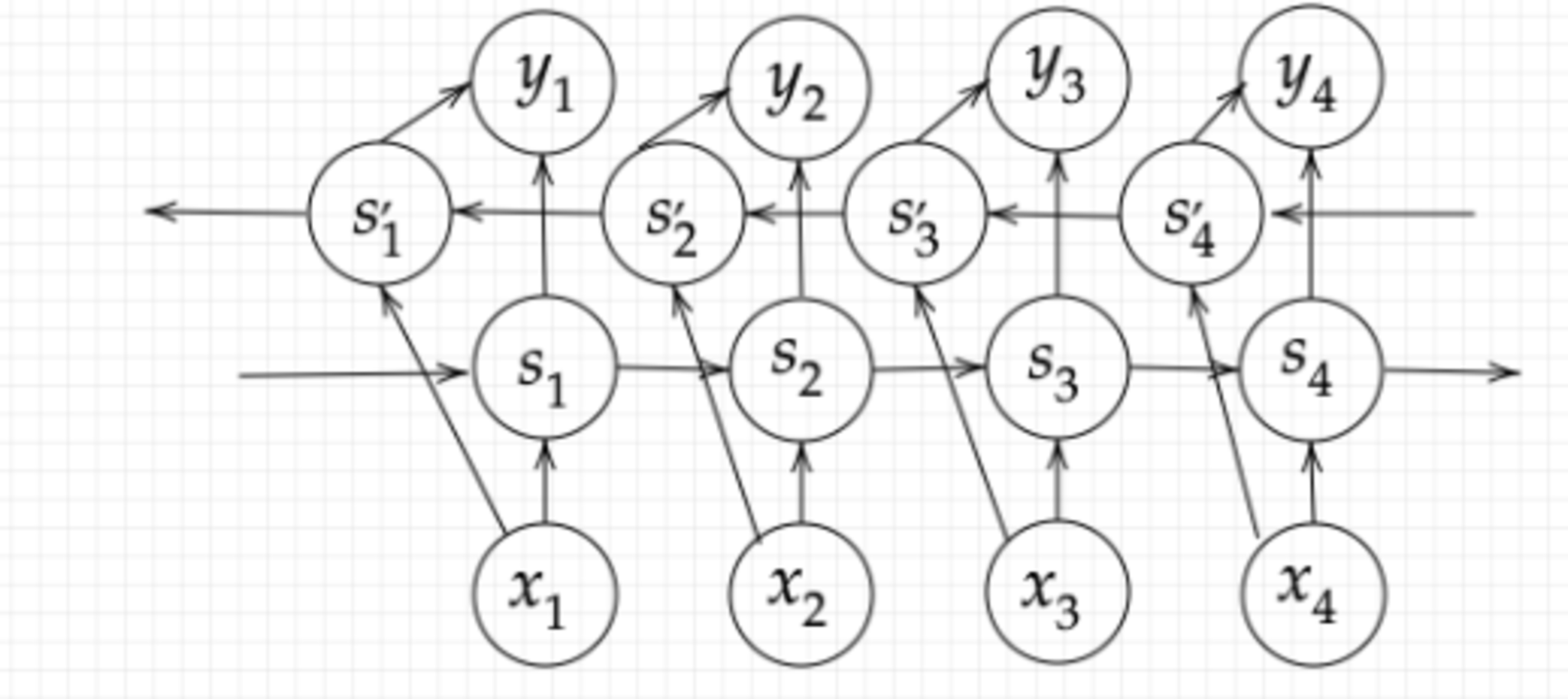 全体像
全体像
実用例として、文章の推敲や機械翻訳等が挙げられる。
Section5:Seq2Seq
Seq2Seqとは、Encoder-Decoderモデルの一種を指す。機械対話や機械翻訳などで使用されている。
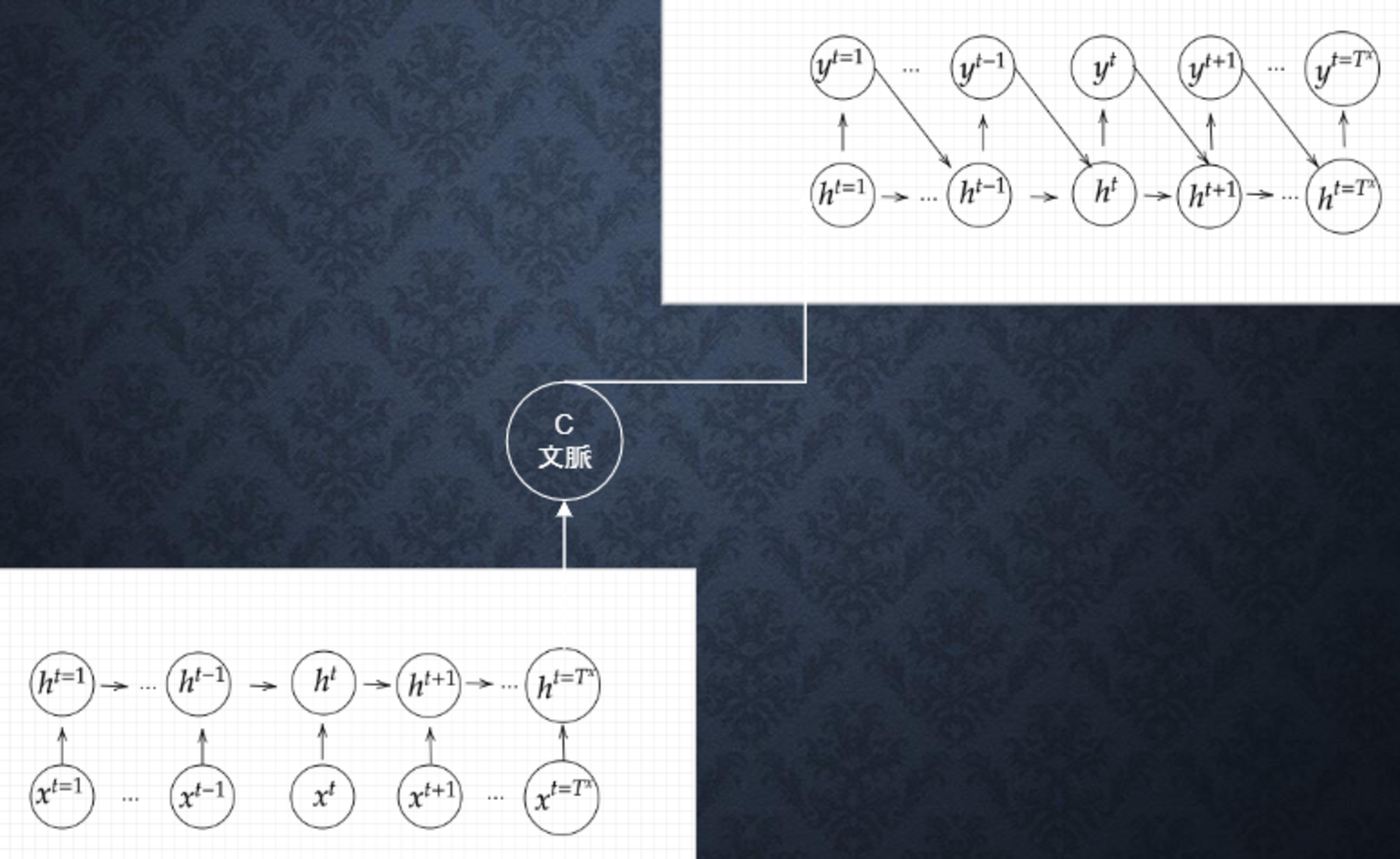 全体図
全体図
Encoder RNN
ユーザーがインプットしたテキストデータを単語等のトークンに区切って渡す構造
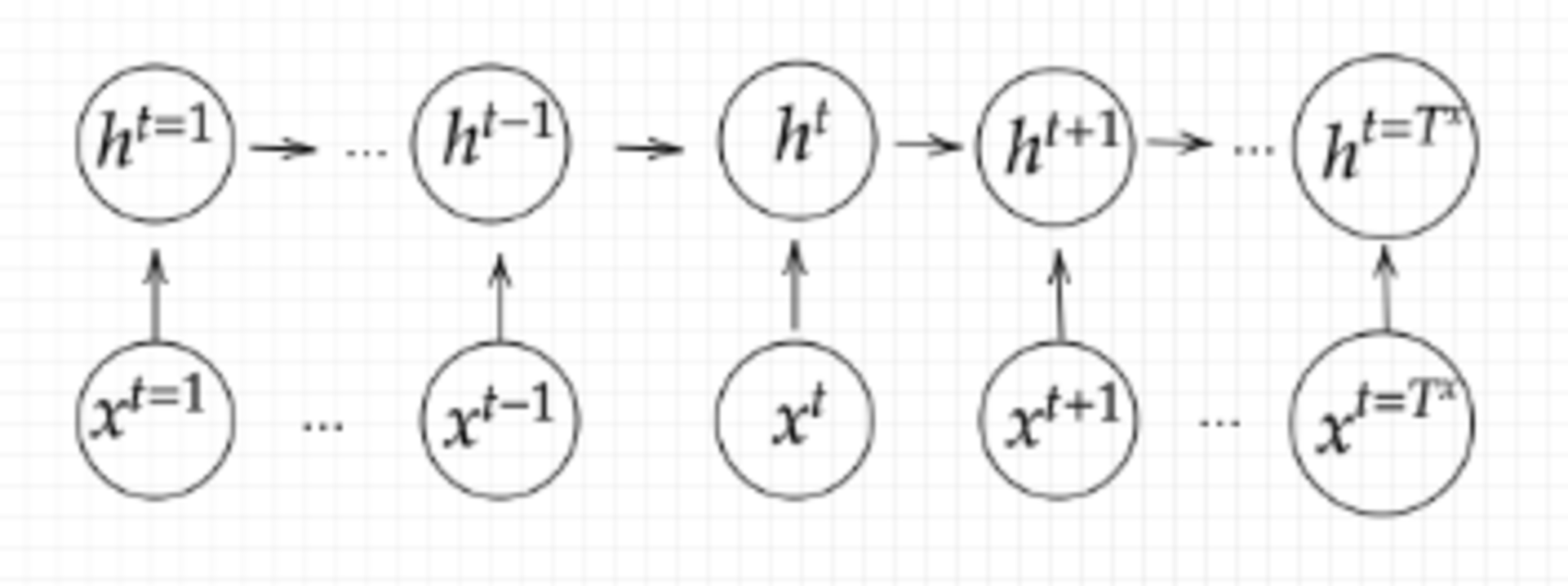
- Taking
文章を単語等のトークン毎に分割し、トークンごとのIDに分割する。 - Embedding
IDから、そのトークンを表す分散表現ベクトルに変換する。 - Encoder RNN
ベクトルを順番にRNNに入力していく。
Encoder RNN 処理手順
- vec1をRNNに入力し、hidden stateを出力する。
- hidden stateと次の入力vec2をまたRNNに入力してhidden stateを出力する
- この流れを繰り返す。
- 最後のvecを入れたときのhidden stateをfinal stateとして保持する。
このfinal stateをthought vectorといい、入力した文の意味を表すベクトルとなり、Decorderへの入力となる。
Decoder RNN
システムがアウトプットデータを、単語等のトークンごとに生成する構造のことを指す。
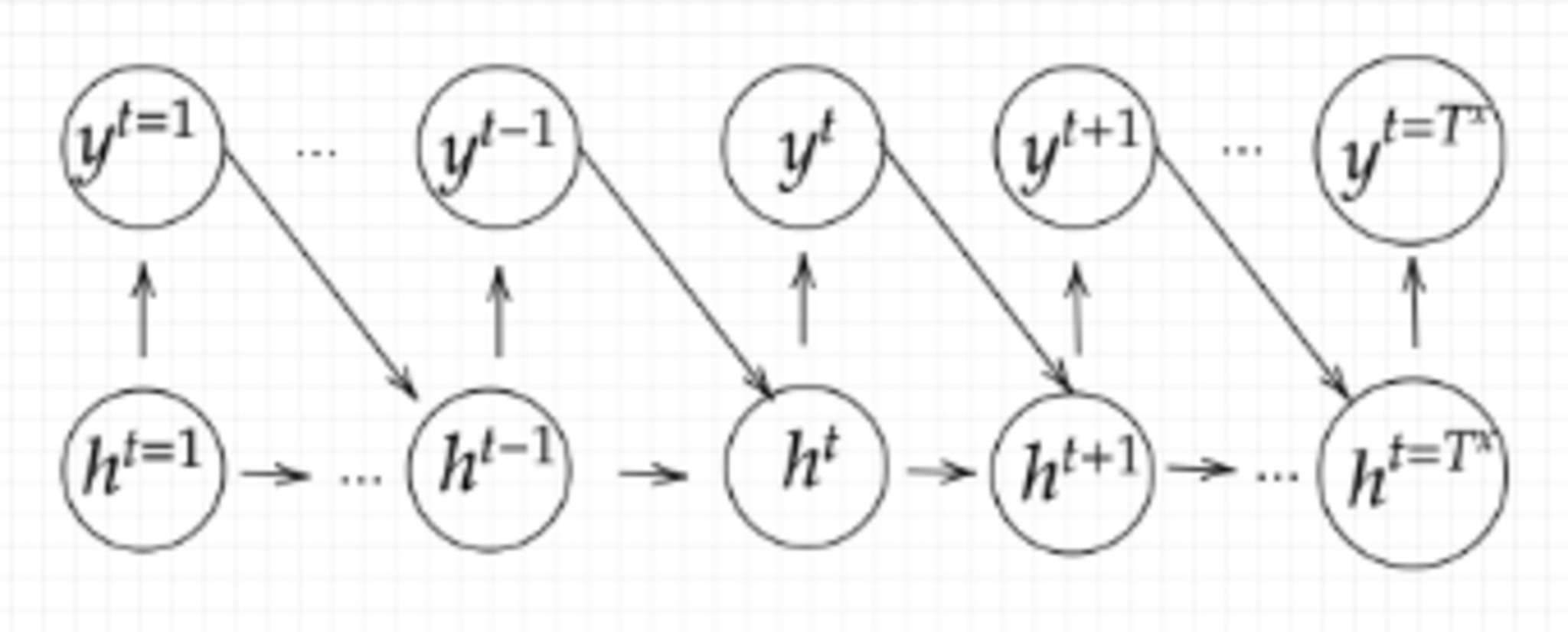
Decoder RNN 処理の流れ
- Decoder RNN:
Encoder RNN のfinal state (thought vector) から、各token の生成確率を出力していく。final state をDecoder RNN のinitial state ととして設定し、Embedding を入力する。 - Sampling:
生成確率にもとづいてtoken をランダムに選ぶ。 - Embedding:
2で選ばれたtoken をEmbedding してDecoder RNN への次の入力とする。 - Detokenize:
1~3 を繰り返し、2で得られたtokenを文字列に直す。
■確認テスト
下記の選択肢から、seq2seqについて説明しているものを選べ。
(1)時刻に関して順方向と逆方向のRNNを構成し、それら2つの中間層表現を特徴量として利用するものである。
(2)RNNを用いたEncoder-Decoderモデルの一種であり、機械翻訳などのモデルに使われる。
(3)構文木などの木構造に対して、隣接単語から表現ベクトル(フレーズ)を作るという演算を再帰的に行い(重みは共通)、文全体の表現ベクトルを得るニューラルネットワークである。
(4)RNNの一種であり、単純なRNNにおいて問題となる勾配消失問題をCECとゲートの概念を導入することで解決したものである。
〇解答
(2)
なお、(1)は「双方向RNN」、(3)は「RNN」、(4)は「LSTM」である。
HRED
Seq2seqの課題として、問に対して文脈も何もなく、ただ応答が行われる続ける、一問一答形式しか対応できなかった。
これを改善したのがHRED(A Hierarchical Recurrent Encoder-Decorder)である。
過去$n−1$の発話から次の発話を生成する。前の単語の流れに即して応答されるため、Seq2Seqより人間らしい文章が生成される。
HREDの構造
HRED = Seq2Seq + Context RNN
- Context RNN: Encoder のまとめた各文章の系列をまとめて、これまでの会話コンテキスト全体を表すベクトルに変換する構造。
HREDの課題
・HREDは確率的な多様性が字面にしかなく、会話の「流れ」のような多様性がない。
・HREDは短く情報量に乏しい答えをしがちである。
VHRED
HREDにVAEの洗潜在変数の概念を追加したものをVHRED(Latent Variable Hierarchical Recurrent Encoder-Decoder)といい、VAEの潜在変数の概念を追加することでHREDの課題を解決した構造のこと。
※VAEは後述
■確認テスト
Seq2SeqとHRED、HREDとVHREDの違いを簡潔に述べよ。
〇解答
- Seq2SeqとHRED:Seq2Seqは一問一答しかできないが、HREDは$n−1$の発話から文脈に応じた回答ができる。
- HREDとVHRED:HREDは発話に多様性がなく情報量に乏しいが、VHREDはその課題を解決し、多様性のある発話をすることができる。
オートエンコーダ
教師なし学習のひとつであり、学習時の入力データは、訓練データのみである(教師データは利用しない)。自己符号化器ともいわれる。
次元削減できるというメリットがある。
オートエンコーダの構造
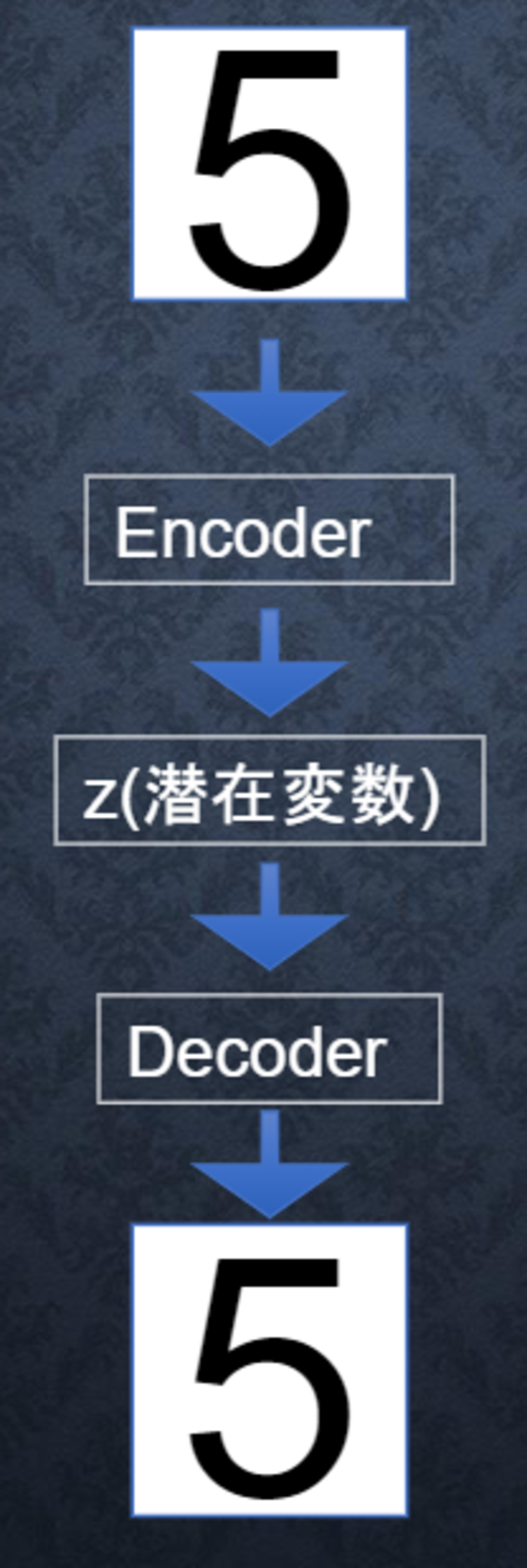
- Encoder:入力データから潜在変数$z$に変換するニューラルネットワークのこと。
- Decoder:潜在変数$z$をインプットとして元画像を復元するニューラルネットワークのこと。
VAE
通常のオートエンコーダの場合、何かしら潜在変数$z$にデータを押し込めているものの、その構造がどのような状態かわからない。
この潜在変数$z$に確率分布$z \sim N(0,1)$を仮定したものをVAE(変分エンコーダ:Variational Auto Encoder)という。これにより、データを潜在変数zの確率分布という構造に押し込めることを可能にする。
■確認テスト
VAEに関する下記の説明文中の空欄に当てはまる言葉を答えよ。自己符号化器の潜在変数に____を導入したもの。
・解答
確率分布$z \sim N(0,1)$。
Section6:Word2vec
RNNでは、単語のような可変長の文字列をNNに与えることはできず、固定長形式で単語を表す必要がある。
学習データからボキャブラリを作成する方法がWord2vecである。
現実的な計算速度とメモリ量で、大規模データの分散表現の学習を実現可能にした。
Word2vecには2種類のモデルが存在する。
- CBoW : 文中の抜けおちた単語の周辺の単語から抜けおちた単語を推定する方法。
- Skip-gram : Skip-gramは、ある単語に隣接する単語を推定する方法。
Section7:Attention Mechanism
Seq2Seqの課題として、長い文章への対応が難しい。Seq2Seqでは、2単語でも100単語でも固定次元ベクトルの中に入力しなければならない。
その解決策として、文章が長くなるほどそのシーケンスの内部表現の次元も大きくなっていく仕組みが必要となる。
そこで「入力と出力のどの単語が関連しているのか」の関連度を学習する仕組みを導入した。この仕組みををAttention Mechanismという。
近年、特に性能が上がっている自然言語のメカニズムである。
■確認テスト
RNNとword2vec、seq2seqとAttentionの違いを簡潔に述べよ。
〇解答
- RNNとword2vec
- RNN : 時系列データを処理するのに適したニューラルネットワーク
- word2vec : 単語の分散表現ベクトルを得る手法
- seq2seqとAttention
- Seq2Seq : ある時系列データから別の時系列データを得るニューラルネットワーク
- Attention : 時系列の中身に対して、関連性に重みをつける手法
演習チャレンジ
テキスト 26ページ
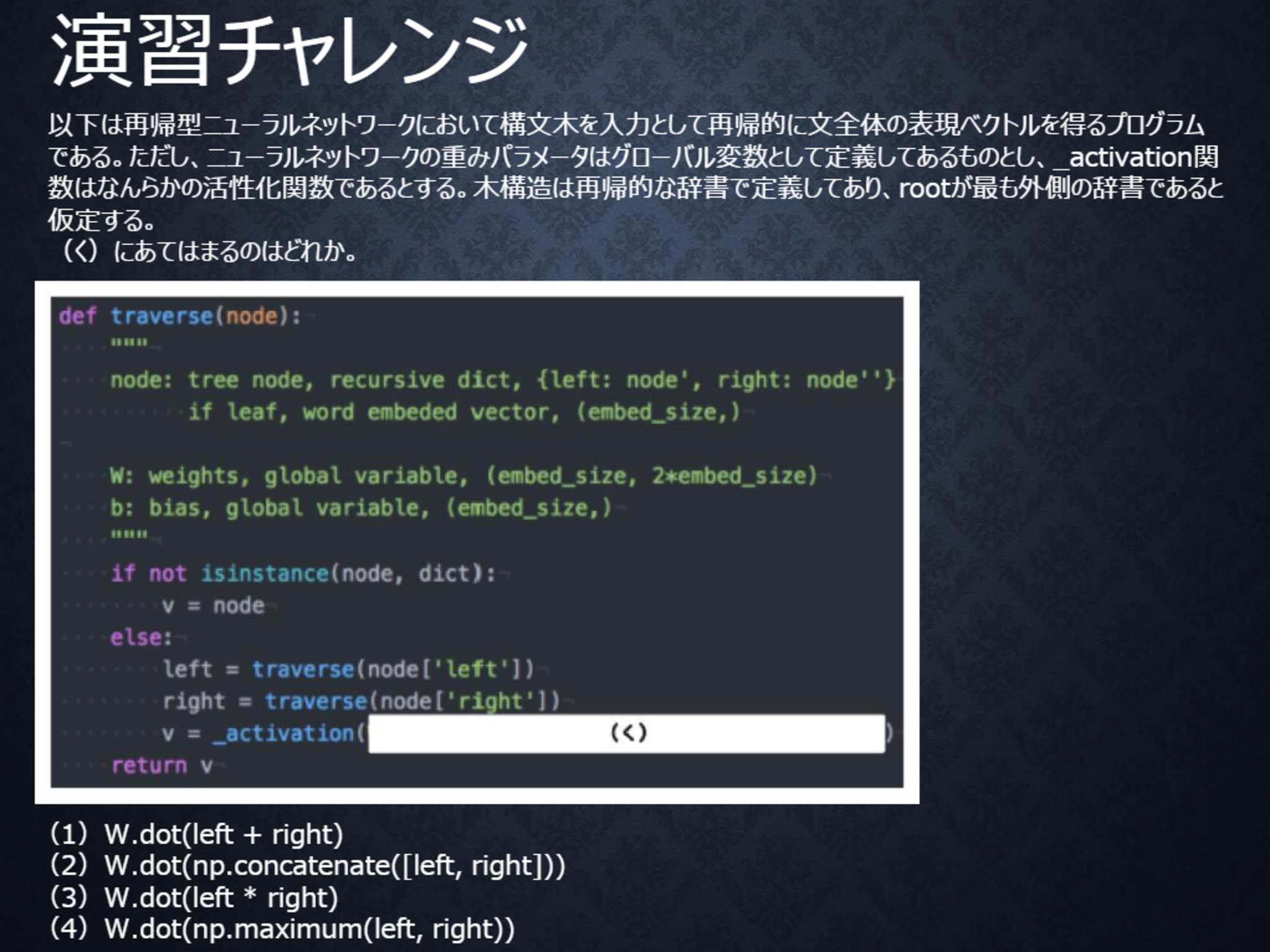
〇解答
(2)
隣接単語(表現ベクトル)から表現ベクトルを作るという処理は、隣接している表現leftとrightを合わせたものを特徴量として、そこに重みを掛けることで実現する。
つまり、W.dot(np.concatenate([left, right]))となる。
テキスト 53ページ
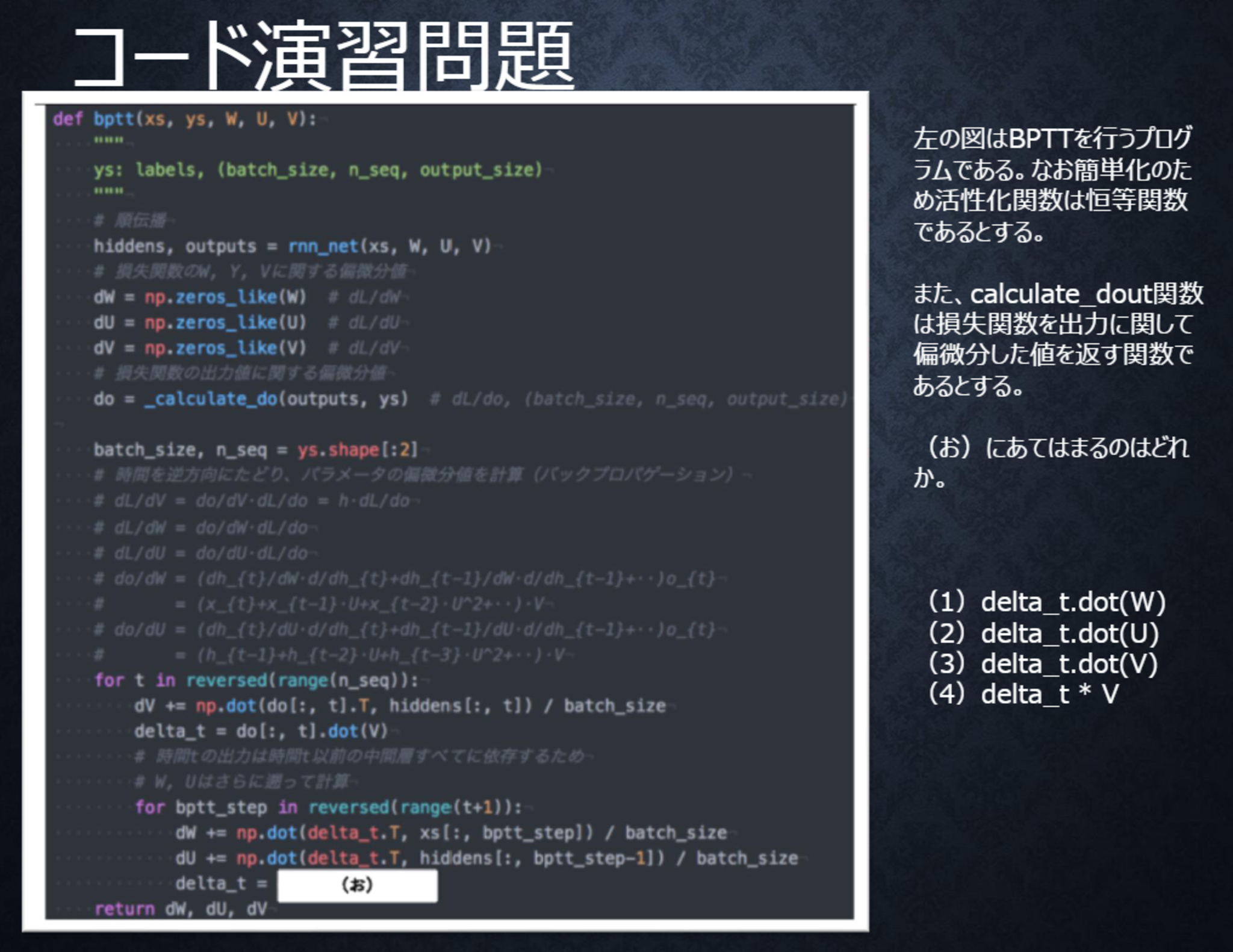
〇解答
(2)
RNNでは中間層出力$h_{t}$が過去の中間層出力$h_{t-1}, \cdots, h_{1}$に依存する。RNNにおいて損失関数を重み$W$や$U$に関して偏微分するときは、それを考慮する必要があり、$dh_{t}/dh_{t-1} = U$であることに注意すると、過去に遡るたびに$U$が掛けられる。
すなわちdelta_t= delta_t.dot(U)である。
テキスト 64ページ
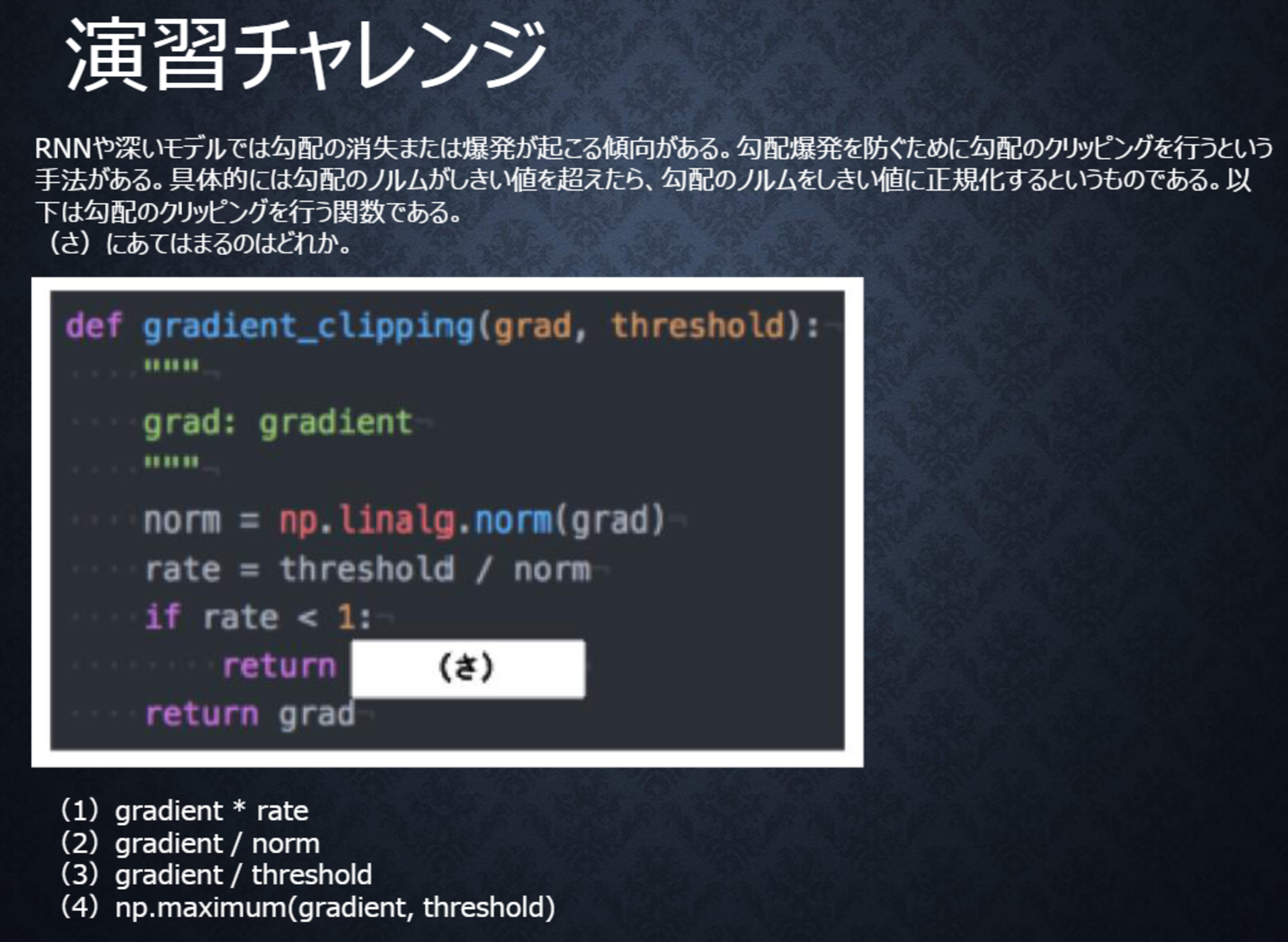
〇解答
(1)
勾配のノルムがしきい値より大きいときは、勾配のノルムをしきい値に正規化するので、クリッピングした勾配は、勾配×(しきい値/勾配のノルム)と計算される。
すなわちgradient * rateである。
テキスト 79ページ
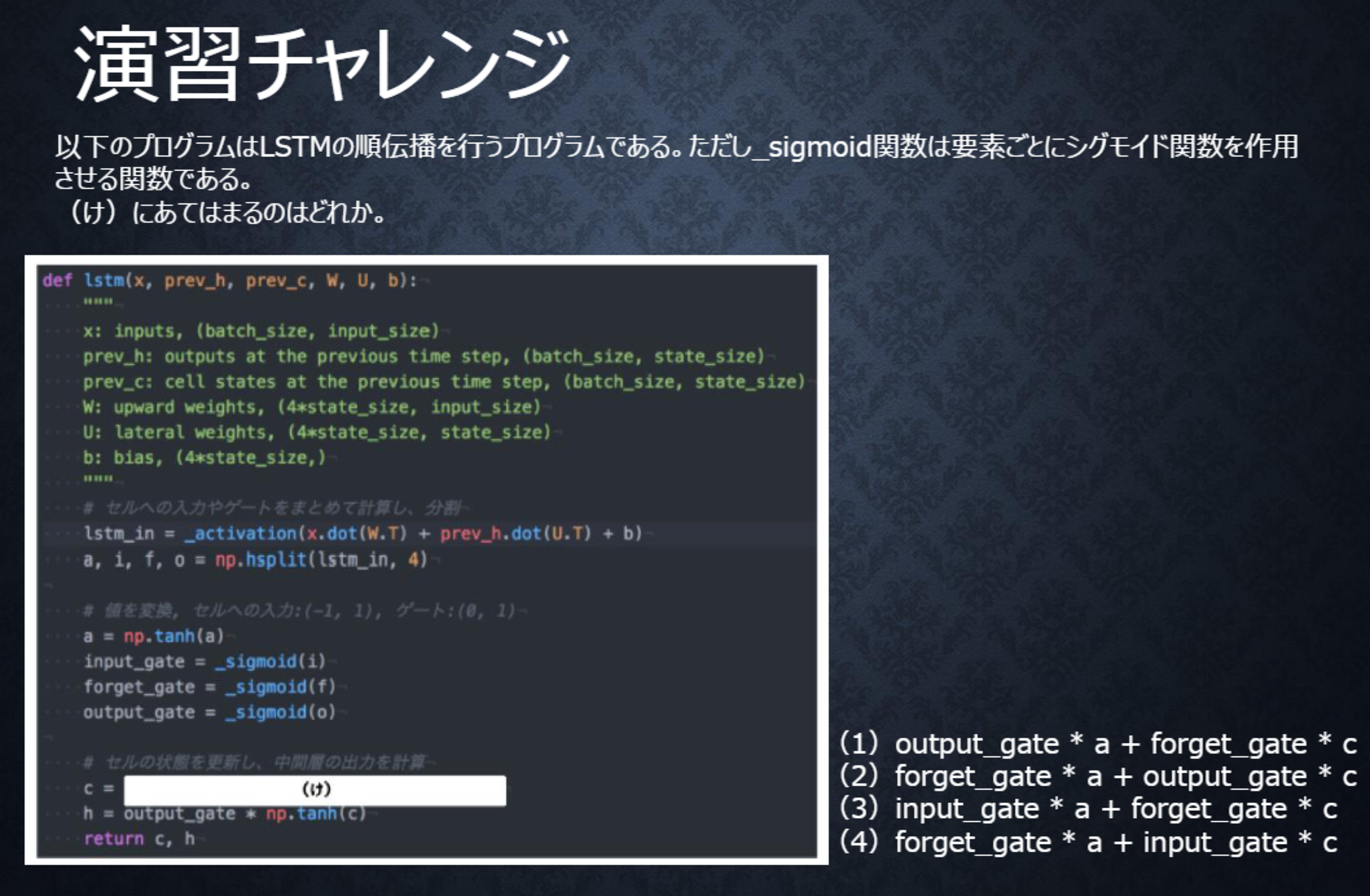
〇解答
(3)
新しいセルの状態は、計算されたセルへの入力と1ステップ前のセルの状態に入力ゲート、忘却ゲートを掛けて足し合わせたものと表現される。
すなわちinput_gate* a + forget_gate* cである。
テキスト 90ページ
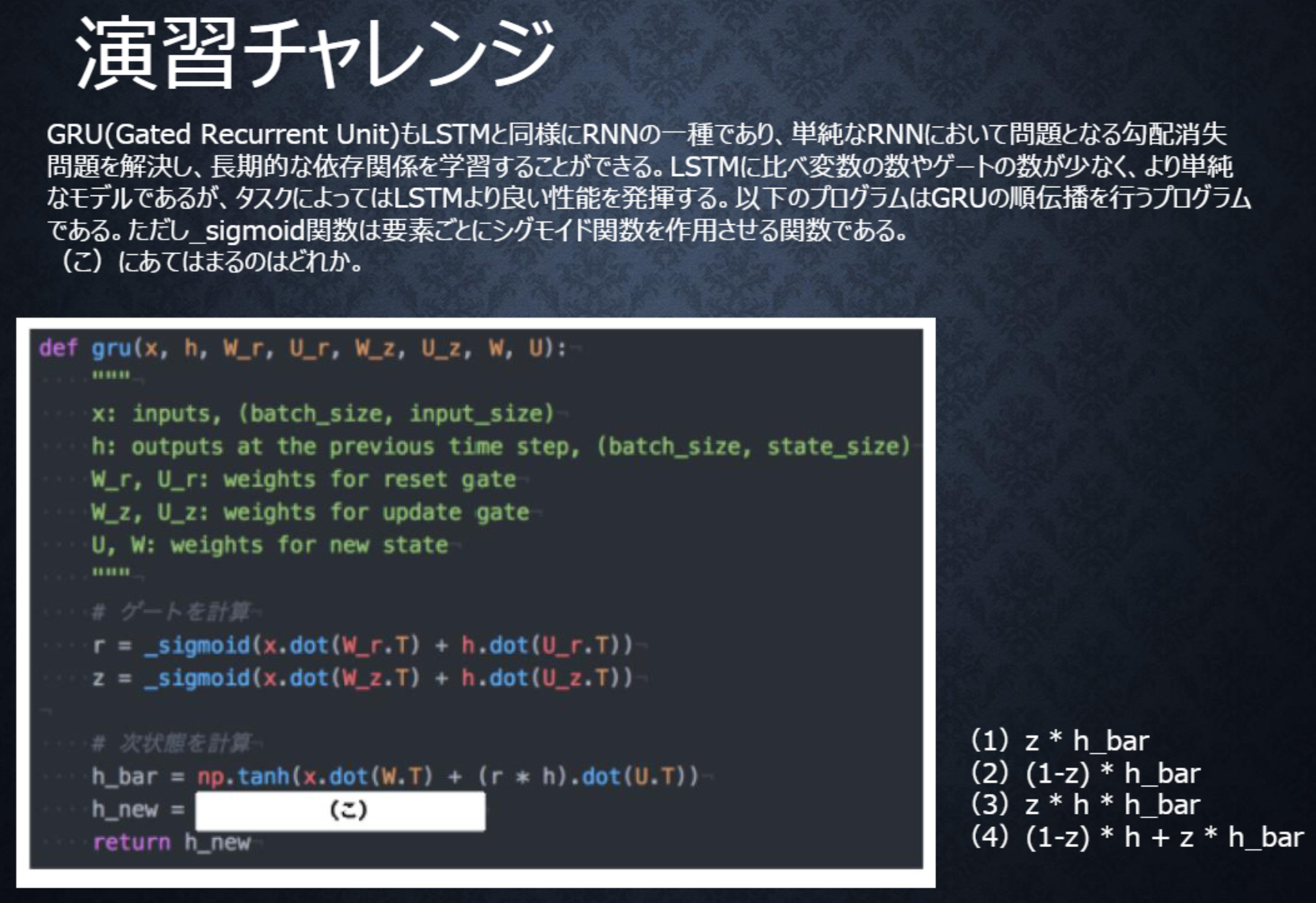
〇解答
(4)
新しい中間状態は、1ステップ前の中間表現と計算された中間表現の線形和で表現される。
すなわち、更新ゲート$z$を用いて、(1-z) * h + z * h_barと表すことができる。
テキスト 95ページ
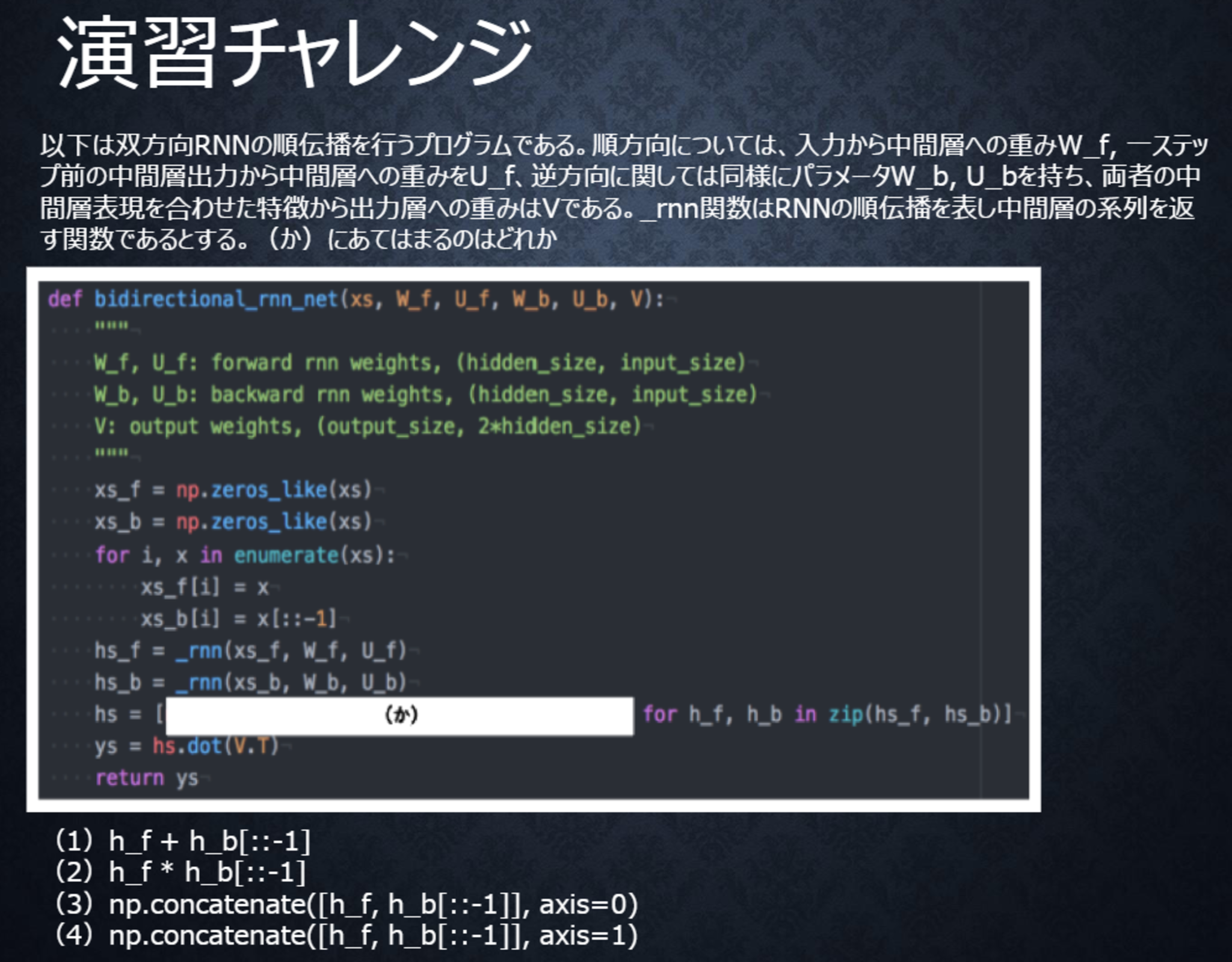
〇解答
(4)
双方向RNNでは、順方向と逆方向に伝播したときの中間層表現をあわせたものが特徴量となるので、np.concatenate([h_f, h_b[::-1]], axis=1)となる。
テキスト 110ページ
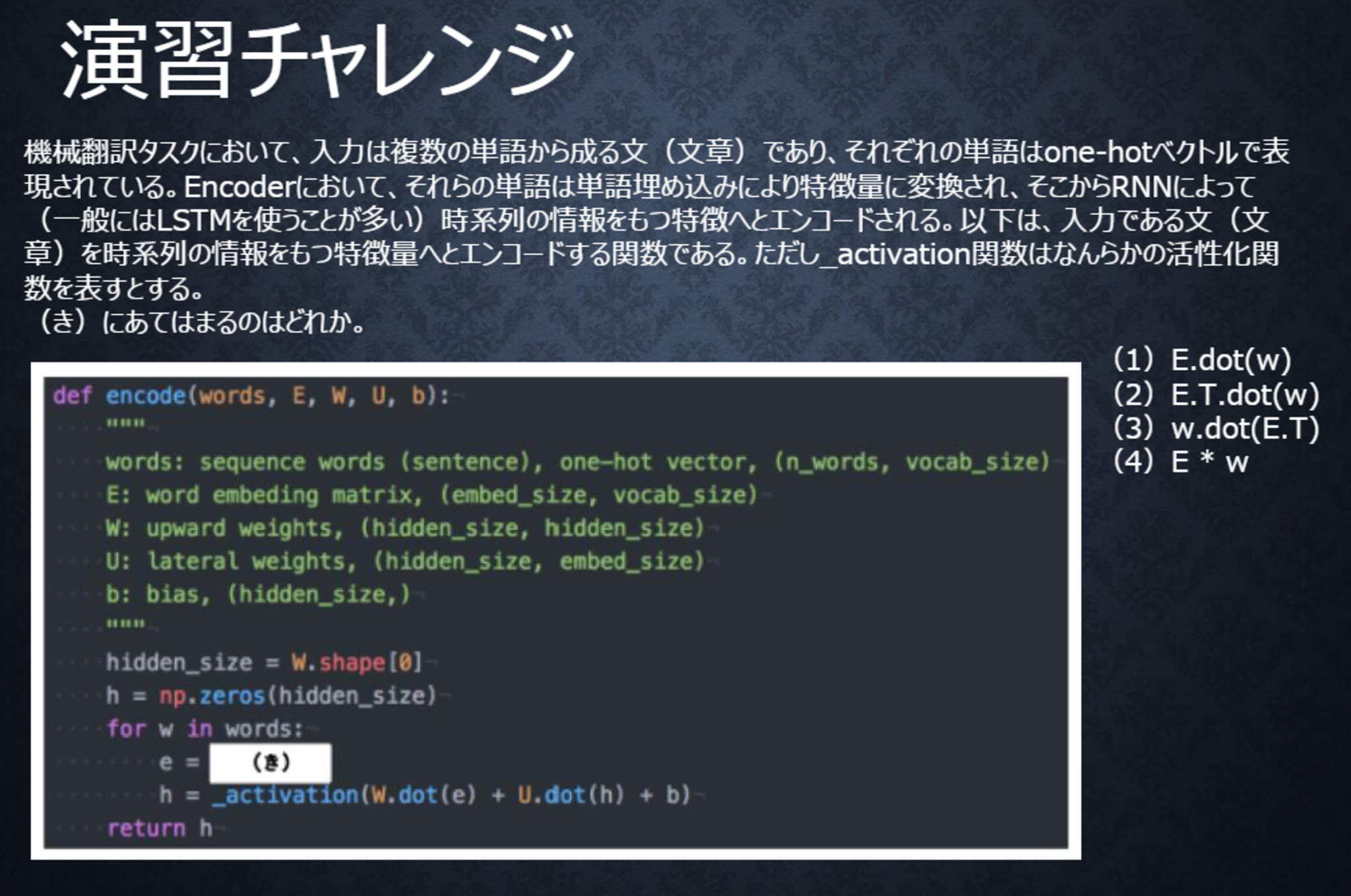
〇解答
(1)
単語wはone-hotベクトルであり、それを単語埋め込みにより別の特徴量に変換する。埋め込み行列Eを用いて、E.dot(w)と書ける。