積分解説7
${}$
この記事では, 以下の積分を解説しようと思います.
$$\int_0^\infty\frac{\log(1+x^2)}{\cosh\pi x+\cos\pi\p}\,dx=\frac{2}{\sin\pi\p}\log\frac{\p\G{\frac\p2}^2\sin\frac{\pi\p}{2}}{2^{1-\p}\pi}$$
${}$
(証明)
以下の積分路に沿った, 関数$\ds f(z)=\frac{\log^2z}{\cosh\pi z-\cos\pi\p}$の積分を考えます.
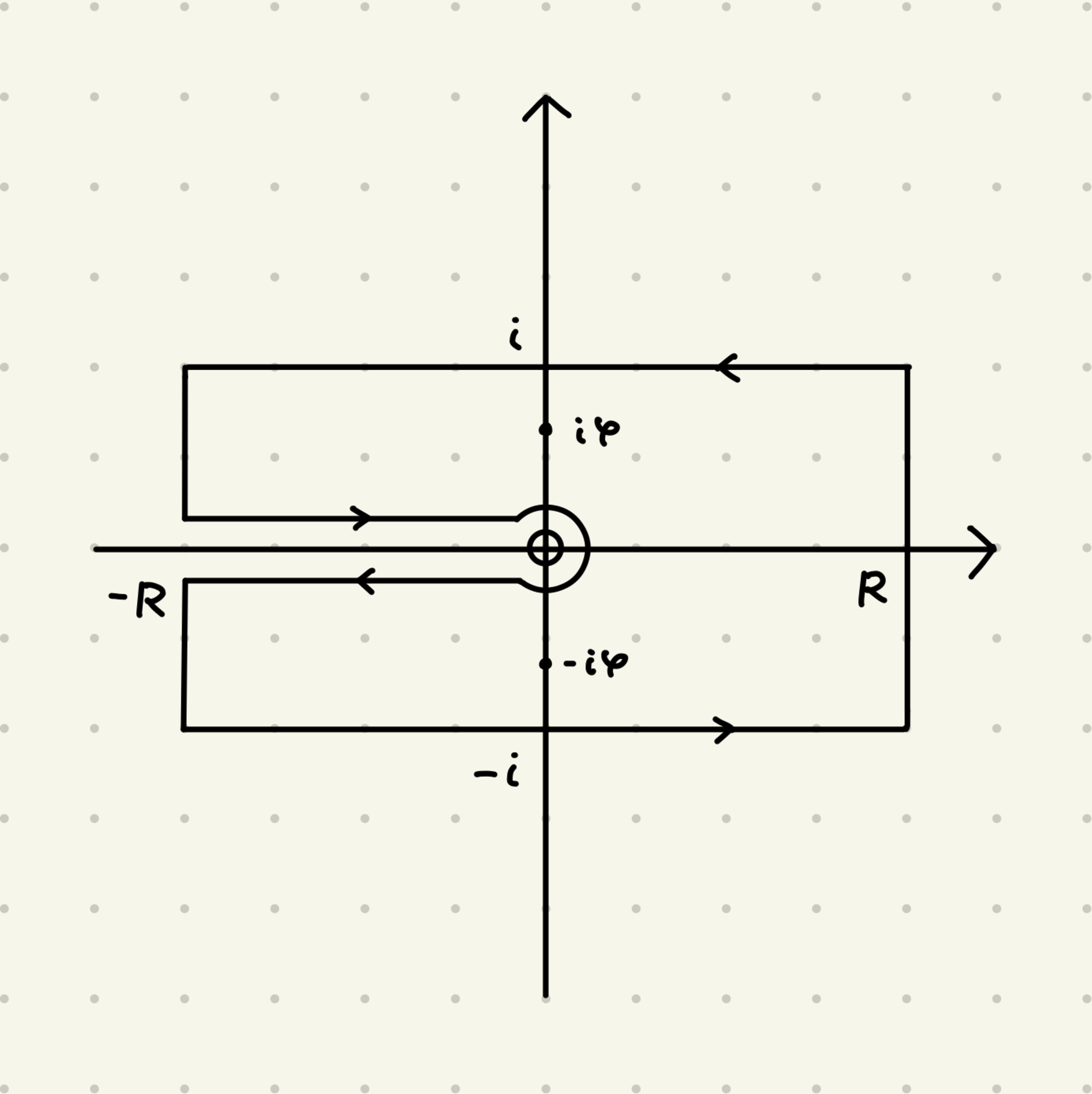積分路1
$R\to\infty$として, 負の実軸に沿った積分は,
$$\begin{align*}
&\int_{-\infty+0i}^{+0i}f(z)\,dz+\int_{-0i}^{-\infty-0i}f(z)\,dz\\[5pt]
=& \int_0^\infty\frac{(\log x+i\pi)^2-(\log x-i\pi)^2}{\cosh\pi x-\cos\pi\p}\,dx\\[5pt]
=&\ 4\pi i\int_0^\infty\frac{\log x}{\cosh\pi x-\cos\pi\p}\,dx\\[5pt]
=&\ 8i\int_0^1\frac{\log\log\tfrac1x-\log\pi}{1-2x\cos\pi\p+x^2}\,dx
\end{align*}$$
ここで, Malmsten's integral ( Wikipedia の5つめの式参照) により $\ds\int_0^1\frac{\log\log\tfrac1x}{1-2x\cos\pi\p+x^2}\,dx=\frac{\pi}{2\sin\pi\p}\log\frac{2^{1-\p}\pi^{2-\p}}{\G{\frac\p2}^2\sin\frac{\pi\p}2}$
また, 普通に計算すると $\ds\int_0^1\frac{dx}{1-2x\cos\pi\p+x^2}=\frac{\pi(1-\p)}{2\sin\pi\p}$ となります.
${}$
次に$\Im z=\pm1$に沿った積分は,
$$\begin{align*}
& \int_{i+\infty}^{i-\infty}f(z)\,dz+\int_{-i-\infty}^{-i+\infty}f(z)\,dz\\[5pt]
=& \int_{-\infty}^\infty\frac{\log^2(x+i)-\log^2(x-i)}{\cosh\pi x+\cos\pi\p}\,dx\\[5pt]
=& \ 2i\int_{-\infty}^\infty\frac{\log(x^2+1)\mathrm{arccot} x}{\cosh\pi x+\cos\pi\p}\,dx\\[5pt]
=& 2\pi i\int_0^\infty\frac{\log(x^2+1)}{\cosh\pi x+\cos\pi\p}\,dx
\end{align*}$$
ただし, $\mathrm{arccot}x+\mathrm{arccot}(-x)=\pi$を利用しました.
${}$
最後に, $z=\pm i\p$での留数は,
$$\begin{align*}
\mathrm{Res}_{z=\pm i\p}f &= \lim_{z\to\pm i\p}\frac{z\mp i\p}{\cosh\pi z-\cos\pi\p}\log^2z\\[5pt]
&= \frac{\log^2(\pm i\p)}{\pi\sinh(\pm i\pi\p)}
\end{align*}$$
より, これらの和は
$$\sum\mathrm{Res}f=\frac{2\log\p}{\sin\pi\p}$$
${}$
以上より, 求める積分を$I(\p)$として,
$$ 2\pi iI(\p)+\frac{4\pi i}{\sin\pi\p}\left(\log\frac{2^{1-\p}\pi^{2-\p}}{\G{\frac\p2}^2\sin\frac{\pi\p}2}-\log\pi^{1-\p}\right)=4\pi i\frac{\log\p}{\sin\pi\p}$$
即ち
$$\int_0^\infty\frac{\log(1+x^2)}{\cosh\pi x+\cos\pi\p}\,dx=\frac{2}{\sin\pi\p}\log\frac{\p\G{\frac\p2}^2\sin\frac{\pi\p}{2}}{2^{1-\p}\pi}$$
を得ます.
${}$
これの両辺を$\p$で微分してから$\p=\frac12$とすることで, 以下を得ます.
$$\begin{align*} \int_0^\infty\frac{\,\log(1+x^2)}{\cosh\pi x}\,dx&=2\log\frac{\ \Gamma(\frac14)^2}{4\pi}\\[5pt] \int_0^\infty\frac{\,\log(1+x^2)}{\cosh^2\pi x}\,dx&=\frac{\,2\,}\pi(2-\gamma-2\log2)\\[5pt] \int_0^\infty\frac{\,\log(1+x^2)}{\cosh^3\pi x}\,dx&=\log\frac{\ \Gamma(\frac14)^2}{4\pi}-\frac{4}{\,\pi^2}(1-G)\\[5pt] \int_0^\infty\frac{\,\log(1+x^2)}{\cosh^4\pi x}\,dx&=\frac{4}{\,3\pi}(2-\gamma-2\log2)-\frac{2}{\,3\pi^3}(7\zeta(3)-8) \end{align*}$$
${}$
読んでくださった方, ありがとうございました.
${}$
${}$