フィボナッチ数列の1項飛ばし数列の漸化式を作ろう ~C-finite数列への誘い~
イントロダクション
フィボナッチ数列$(F_n)_{n \in \N}$を
$$
F_0 = 0, F_1 = 1, F_{n+2} = F_{n+1} + F_n \text{ (for $n \in \N)$}
$$
で定めます。
最初の方をいくつか見てみると次のようになっています。
| $n$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ |
|---|---|---|---|---|---|---|---|---|---|
| $F_n$ | $0$ | $1$ | $1$ | $2$ | $3$ | $5$ | $8$ | $13$ | $21$ |
では問題です。
フィボナッチ数列の1個飛ばし数列$(G_k)_{k \in \N}$を
$$
G_k = F_{2k}
$$
で定めます。フィボナッチ数列のときと同様の漸化式を$(G_k)_{k \in \N}$に対して探してください。
いきなり答えを書くと
$$
G_{k+2} = 3 G_{k+1} - G_k
$$
です。
たとえば上の表を見ると$3 G_3 - G_2 = 3 F_6 - F_4 = 3 \cdot 8 - 3 = 21 = F_8 = G_4$なので$k=4$では成り立っています。一般に成り立つことは数学的帰納法で示すことができます。
では、これはどう導出すればいいのか?1個飛ばしではなくて、任意に固定した$m \in \N$について$m$の倍数番目を取りだした数列だとどうか?一般の定数係数で斉次の線形漸化式で定義される数列に対して適用できる方法はあるのでしょうか?
こういったことを今から議論していきます。
導出
シフト演算というものを定義します。これは数列を受け取って数列を返す関数$D$で
$$D\colon (x_n)_{n \in \N} \mapsto (x_{n+1})_{n \in \N}$$
と定義されます。つまり初項を捨てて、あとの項は1個左にずらすという写像です。
このシフト演算を使うとフィボナッチ数列の漸化式$F_{n+2} = F_{n+1} + F_n$は次のように表現できます。
$$(D^2 - D - I) (F_n)_{n \in \N} = 0$$
ここで左辺の$D^2$は$D$二つの合成、$I$は恒等変換、右辺の$0$は常に$0$な数列を表すことにします。
この式の両辺に左側から$(D^2 + D - I)$を作用させます。
$$(D^2 + D - I)(D^2 - D - I) (F_n)_{n \in \N} = 0$$
左辺を計算してみると
$$((D^2 - I)^2 - D^2) (F_n)_{n \in \N} = 0$$
で
$$(D^4 - 3D^2 + I) (F_n)_{n \in \N} = 0$$
となります。
さて、これをもとの漸化式のような形で書き直すとどうなるでしょうか。次のようになります:
$$F_{n+4} - 3 F_{n+2} + F_n = 0.$$
ここの$n$に$2k$を代入すればほしい式そのものですね。これで導出できました。
考察と一般化
上の導出では$(D^2 + D - I)$というものを天下りに与えて、計算するとうまくいっていました。これは何をやっているのでしょうか?
$g(x) = x^2 - x - 1$と多項式を定義したときに$g(D) (F_n)_{n \in \N} = 0$ですが、このとき$h(x) = x^2 + x - 1$という別の多項式を与えたら、$g(x)h(x) = x^4 - 3x^2 + 1$と偶数次数の元だけ残ったことがポイントです。
つまり、多項式$g(x)$について多項式$h(x), f(x)$であって
$$g(x)h(x) = f(x^2)$$
となることを見つけられたのがよかったのです。
このことを一般に述べると次です。
自然数$m \ge 1$を固定しましょう。定数係数で斉次の線形漸化式
$$
a_{n+r} + c_{r-1} a_{n+r-1} + \dots + c_1 a_{n+1} + c_0 a_n = 0
$$
が与えられます。今$c_0, \dots, c_{r-1}$は定数で$c_0 \ne 0$とします。多項式$g(x)$を
$$
g(x) = c_{r-1} x^{r-1} + \dots + c_1 x + c_0
$$
で定めるとシフト演算$D$を使って漸化式は
$$
g(D) (a_n)_{n \in \N} = 0
$$
と書けます。
ここに多項式$h(x), f(x)$であって
$$g(x)h(x) = f(x^m)$$
なるものが見つけられたとしたら
$$
f(D^m) (a_n)_{n \in \N} = 0
$$
となるので
$$
f(D) (a_{mk})_{k \in \N} = 0
$$
となり、多項式$f$の係数で数列$(a_{mk})_{k \in \N}$の漸化式が得られます。
多項式$f$の存在
さて、問題は与えられた多項式$g(x)$に対して
$$
g(x)h(x) = f(x^m)
$$
となる多項式$h(x), f(x)$を求めることに帰着しました。これはいつでも存在するでしょうか。
考えている係数体が標数$0$という仮定のもとでYesです。
$K$を標数$0$の体とする。$g(x) \in K[x]$を多項式とする。$m$を$1$以上の自然数とする。
このとき$h(x), f(x) \in K[x]$があって
$$
\deg g(x) = \deg f(x)
$$
かつ
$$
g(x)h(x) = f(x^m)
$$
となる。
1の原始$m$乗根の一つを$\zeta$とおき、$\zeta$を添加した体$L = K(\zeta)$で考える。$F(x) \in L[x]$を次で定める。
$$
F(x) = \prod_{\xi^m = 1} g(\xi x)
$$
とおく。
$\xi = 1$のときの因子を含んでいるので明らかに$g(x) \divides F(x)$である。
$F(x) \in K[x]$を示す。$K$が標数$0$なので$L/K$は分離拡大である。また$\zeta$の$K$上共役な元は1の原始$m$乗根なので$L$に入っている。よって$L/K$は正規拡大。したがってガロアの基本定理より$\Gal(L/K)$の任意の元で不変な$L$の元全体の集合は$K$に等しい。
今多項式$F(x)$に$\Gal(L/K)$の元$\sigma$を作用させると、$\sigma$は$\zeta$をある$\zeta^k$ ($k$は$m$と互いに素な整数)に写すものなので、$F(x)$に$\sigma$を作用させた多項式$F^\sigma(x)$を考えると
\begin{align*}
F^\sigma(x) &= \left(\prod_{\xi^m = 1} g(\xi x)\right)^\sigma \\
&= \left(\prod_{0\le i < m} g(\zeta^i x)\right)^\sigma \\
&= \left(\prod_{0\le i < m} g(\sigma(\zeta)^i x)\right) \\
&= \left(\prod_{0\le i < m} g(\zeta^{ki} x)\right) \\
&= \left(\prod_{0\le j < m} g(\zeta^j x)\right) \\
&= F(x)
\end{align*}
となり不変。よって、$F(x) \in K[x]$である。
また、任意の$1$の$m$乗根$\xi'$について
$$
F(\xi' x) = \prod_{\xi^m = 1} g(\xi \xi' x) = \prod_{\xi^m = 1} g(\xi x) = F(x)
$$
なことから$F(x)$は$m$の倍数の次数の項しかないことが分かる (標数$0$なことを再び使った)。
そこで$f(x^m) = F(x)$となる多項式$f(x)$がある。$F(x) \in K[x]$なので$f(x) \in K[x]$である。
$\deg F(x) = m \cdot \deg g(x)$を考えると、$\deg g(x) = \deg f(x)$が分かる。
フィボナッチ数列の2項飛ばし、3項飛ばし, etc
2項飛ばし
さて一般的な方法が分かったのでフィボナッチ数列の2項飛ばしや3項飛ばしなどに応用してみましょう。
まずは2項飛ばし ($m=3$)です。
$g(x) = x^2 - x - 1$に対して
$$
F(x) = g(x) g(\omega x) g(\omega^2 x)
$$
を計算しましょう。ここで$\omega$は$1$の原始$3$乗根です。
.........
$$
F(x) = x^6 - 4 x^3 - 1
$$
と出ました。
よって
$$
f(x) = x^2 - 4 x - 1
$$
で
$$
F_{3(n+2)} = 4 F_{3(n+1)} + F_{3n}
$$
です!
3項飛ばし
次は3項飛ばし ($m=4$)です。
$$F(x) = g(x) g(ix) g(-x) g(-ix)$$を計算しましょう。
.........
$$
F(x) = x^8 - 7 x^4 + 1
$$
と出ました。
よって
$$
f(x) = x^2 - 7 x + 1
$$
で、
$$
F_{4(n+2)} = 7 F_{4(n+1)} - F_{4n}
$$
です。
4項飛ばし
次は4項飛ばし ($m=5$)です。しんどいのでMathematicaにやってもらいました。
$$
f(x) = x^2 - 11 x^5 - 1
$$
で、
$$
F_{5(n+2)} = 11 F_{5(n+1)} + F_{5n}
$$
です。
5項飛ばし
次は5項飛ばし ($m=6$)です。同じくMathematicaで。
$$
f(x) = x^2 - 18 x^5 + 1
$$
で、
$$
F_{6(n+2)} = 18 F_{6(n+1)} - F_{6n}
$$
です。
$m$を動かしたときに何か係数に規則性があるのか…?という疑いも生じてきますが、この辺で終わりにします。
まとめ
定数係数で斉次の線形漸化式を満たす数列 (こういうのをC-finite sequenceというそうです)の固定した自然数の倍数番目の項を取り出した数列の漸化式を与える方法を紹介しました。それをフィボナッチ数列に応用してみました。
この話は参考文献のThe Concrete Tetrahedronの定理4.2がもとになっています。C-finite sequenceの固定した自然数の倍数番目の項を取り出した数列もまたC-finite sequenceとなることが書かれているんですが、証明は読者の演習問題となっています。そこで考えてみたという次第です。
まだ読んでいる途中なのですが、なかなか面白い本です。
追記 (2021/7/4)
以上を見ると
- $F_{n+2} - F_{n+1} - F_n = 0$
- $F_{n+4} - 3 F_{n+2} + F_n = 0$
- $F_{n+6} - 4 F_{n+3} - F_n = 0$
- $F_{n+8} - 7 F_{n+4} + F_n = 0$
- $F_{n+10} - 11 F_{n+5} - F_n = 0$
- $F_{n+12} - 18 F_{n+6} + F_n = 0$
ですね。規則性が気になります。最後の項は$(-1)^m F_n$でしょうね。真ん中の項の係数はどうでしょうか。OEISに投げてみました。
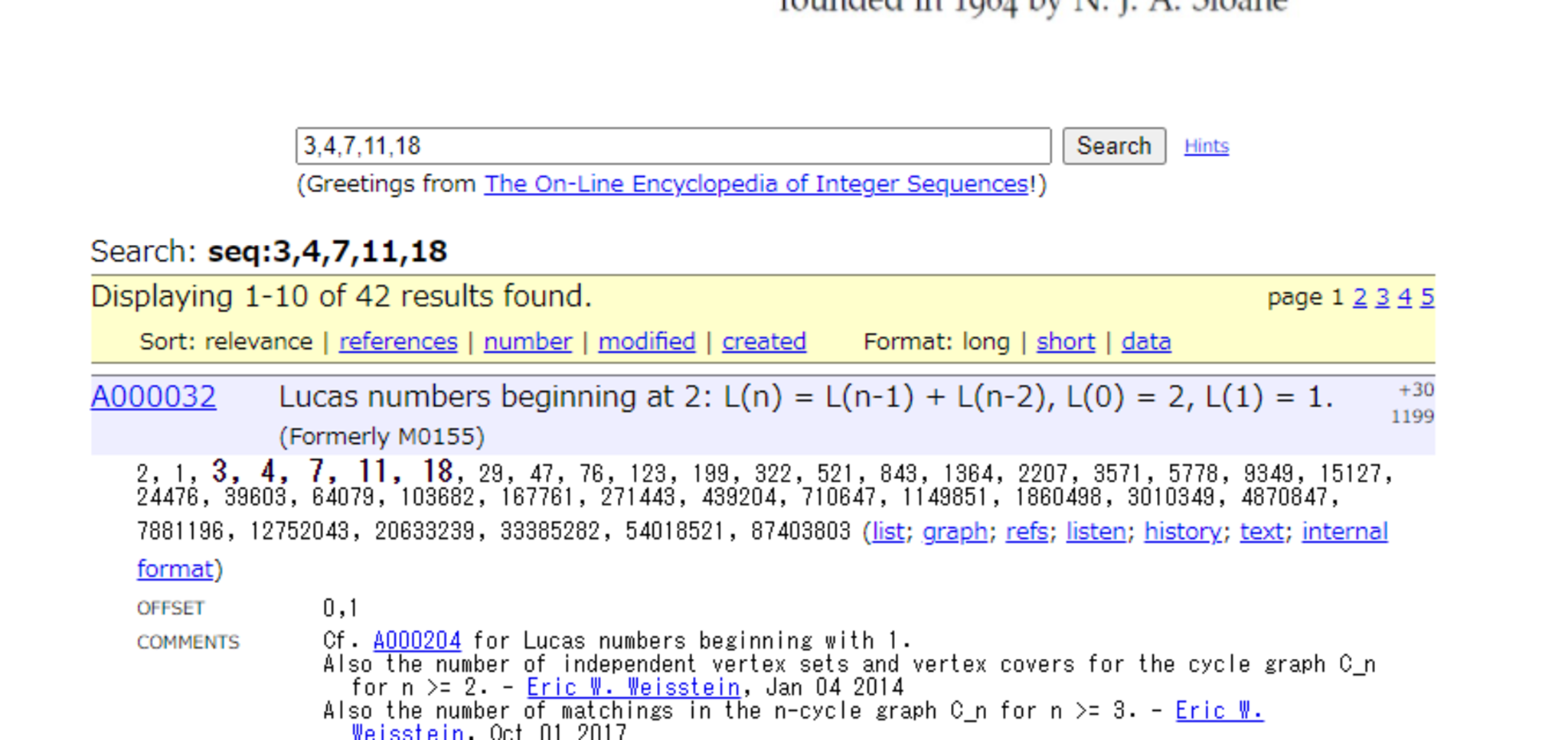 OEIS
OEIS
なんと、真ん中の項の係数はリュカ数列の模様です!つまり、次の式ということです。
$$F_{n+2m} - L_m F_{n+m} + (-1)^m F_n = 0$$
これの証明はたとえば以下のようにすればいいでしょう。
方程式$x^2-x-1=0$の解を$\varphi_1 = (1+\sqrt{5})/2, \varphi_2 = (1-\sqrt{5})/2$とします。解と係数の関係より$\varphi_1 \varphi_2 = -1$です。多項式$f(x) = x^2 - L_m x + (-1)^m$が$(x^2-x-1) \divides f(x^m)$を満たすことを言えばよいでしょう。そのためには$f(\varphi_1^m)=f(\varphi_2^m)=0$を言えばいいです。これは言えて、実際、たとえば$\varphi_1$の方は
\begin{align*}
f(\varphi_1^m) &= (\varphi_1)^{2m} - L_m (\varphi_1)^m + (-1)^m \\
&= (\varphi_1)^{2m} - ((\varphi_1)^m + (\varphi_2)^m) (\varphi_1)^m + (-1)^m \\
&= -(\varphi_1 \varphi_2)^m + (-1)^m \\
&= 0
\end{align*}
なのでOKです。ここにリュカ数列の一般項$L_m = (\varphi_1)^m + (\varphi_2)^m$を使いました。
追記2 (2021/7/10) 正標数の場合
定理1は標数$0$の場合を扱いましたが、実は正標数でも成り立ちます。この節は @waidotto さんの助言をもとに執筆しました。
$K$を体とする。$g(x) \in K[x]$を多項式とする。$m$を$1$以上の自然数とする。
このとき$h(x), f(x) \in K[x]$があって
$$
\deg g(x) = \deg f(x)
$$
かつ
$$
g(x)h(x) = f(x^m)
$$
となる。
標数$0$の場合は証明したので、標数$p > 0$の場合を示す。$m = p^e \cdot q$で$q$は$p$と互いに素とする。
$$g(x) = c_n x^n + \dots + c_1 x + c_0$$
と表したときに、
$$g^*(x) = (c_n)^{p^e} x^n + \dots + (c_1)^{p^e} x + (c_0)^{p^e}$$
とおく。すると、フロベニウス写像$x \mapsto x^p$の準同型性より、
$$
g(x)^{p^e} = g^*(x^{p^e})
$$
が分かる。
今、原始$q$乗根$\zeta$を考えて、$L = K(\zeta)$とおく。$p$と$q$が互いに素なのでこれは考えることができる。定理1の証明と同様に$F(x) = \prod_{0 \le i < q} g^*(\zeta^i x)$を考えよう。
$L/K$は分離拡大である。なぜなら、多項式$x^q - 1$はその微分$q x^{q-1}$と互いに素だから分離多項式である。よってその約元である$\zeta$の最小多項式も分離多項式であるからである。よって定理1の証明と同様に$F(x) \in K[x]$が導かれる。
$F(x) = f(x^q)$となる$f(x) \in K[x]$があることも同様にわかる。ただしこの証明では$q$で割る操作が必要になるのだが、$p$と$q$が互いに素なおかげで可能なことに注意しておく。
したがって、$\deg f(x) = \deg g^*(x) = \deg g(x)$かつ$g(x) \divides f(x)$となり証明が終わる。
実際、$g(x) \divides g(x)^{p^e} = g^*(x^{p^e}) \divides F(x^{p^e}) = f(x^m)$である。
