弦グラフの性質

グラフ理論

430

はじめに

基礎的な用語（サイクル、完全グラフなど）は既知であるものとして扱います。

弦グラフ

グラフ$G$に存在する任意の長さ$4$以上の誘導サイクルが弦を持つ、つまり、サイクルを構成しないがサイクル内のある$2$頂点を結ぶような辺が存在するとき、$G$を弦グラフと呼ぶ。

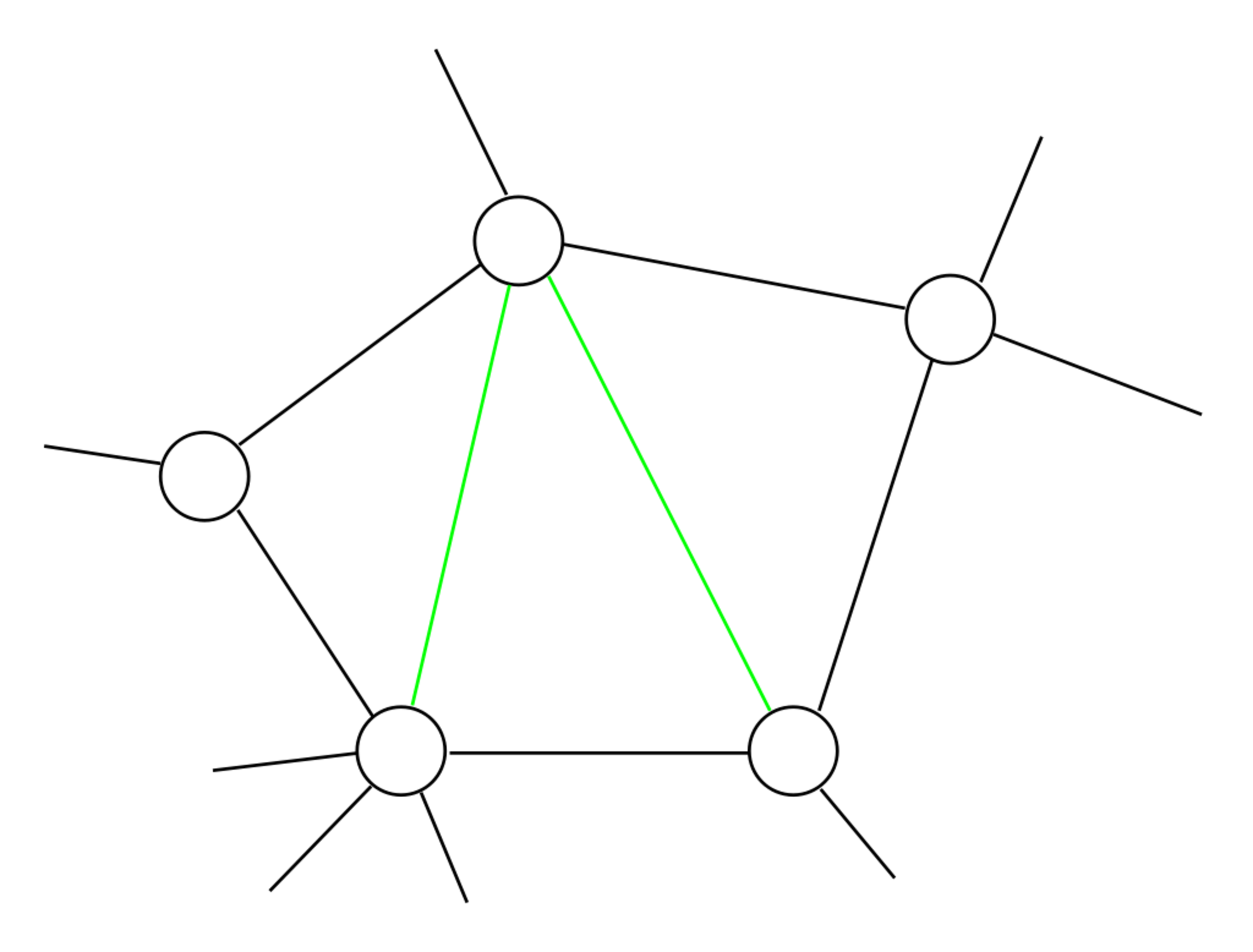弦グラフ

ところで、グラフ理論にはperfect elimination orderingという概念もあります（常に存在する訳ではないことに注意）。

perfect elimination ordering

グラフの頂点に対する順序がperfect elimination orderingであるとは、各頂点$v$について、$v$自身と$v$に隣接かつ$v$より順序が後ろである頂点集合の誘導グラフが完全グラフであることを指す。

perfect elimination ordering

一見、両者は全く無関係なものに感じますが、実は次の定理が成り立ちます。

$G$は弦グラフである$ \Longleftrightarrow $$G$がperfect elimination orderingを持つ

今回はこの定理を証明していきます。

準備

$G$の頂点$v$において、$N(v)$を$v$自身と$v$に隣接する頂点集合とする。

$v$がsimplicialであるとは、$N(v)$の誘導グラフが完全グラフであることを言う。

定義より、完全グラフ内の任意の頂点はsimplicialである。

$G$が弦グラフなら$1$つ以上のsimplicialな頂点が存在する。さらに$G$が完全グラフでないならば、$G$は$2$つの隣接しないsimplicialな頂点を持つ。

(i) $|G|=2$のとき
頂点$u,v$の間に辺があるなら$G$は完全グラフ、そうでないなら$u,v$は明らかにsimplicialである。

(ii) $|G|< k$で補題が成り立つと仮定し、$|G|=k$のとき
$G$が完全グラフである場合は明らか。そうでないとき、隣接しない頂点$a,b$を取ってくることができる。$a,b$を分離する集合(つまり、$G$の頂点集合から引くと$a,b$が別の連結成分になるような集合)のうち、サイズが最小のものを$S$とする。$S$によって分離された$a,b$の連結成分を$G_a,G_b$と表す。

もし$S$が完全グラフでない場合、隣接していない頂点$x,y \in S$が存在し、$S$の最小性からサイクル$\{a,\ldots,x,\ldots,b,\ldots,y,\ldots,a\}$が存在する。しかし、このサイクルは長さ$4$以上かつ弦がないので、$G$が弦グラフであることに矛盾する。よって、$S$は完全グラフ。

$G_a+S$は$G$の誘導グラフだから弦グラフであり、$|G_a+S|< k$を満たす。よって、仮定より$G_a+S$は完全グラフまたは2つの隣接しないsimplicialな頂点を持つ。もし$G_a+S$が完全グラフならば$G_a$の頂点は全てsimplicialである。そうでないなら、$2$つの隣接しないsimplicialな頂点が存在し、$S$は完全グラフなのでどちらかは$G_a$に入っている。つまり、$G$についてsimplicialな頂点が$G_a$の中に$1$つ以上存在する。対称性より$G_b$にも同様の議論ができるので、$G_a,G_b$から一つずつsimplicialな頂点を取ってくると、両者は隣接していない。

定理1の証明

perfect elimination orderingを持つ$ \Rightarrow $弦グラフである

対偶を示す。$G$が弦グラフでないなら、弦のないサイクル$s_0,s_1,\ldots,s_k=s_0(k>3)$が存在する。頂点の順序で$s_i$が最も前であったとすると、$s_{i-1},s_{i+1}$は異なる頂点であり隣接もしていない。よって、$s_i$より順序が後ろの頂点集合は完全グラフにならないので、任意の順序はperfect elimination orderingとならない。