ピクロスの解は1通りかどうか
ピクロスの解は$1$通り
結論から言うと、偽です。
概要
簡単な証明の方法です。
例えば、以下のパターンは解が2通りに決まってしまいます。
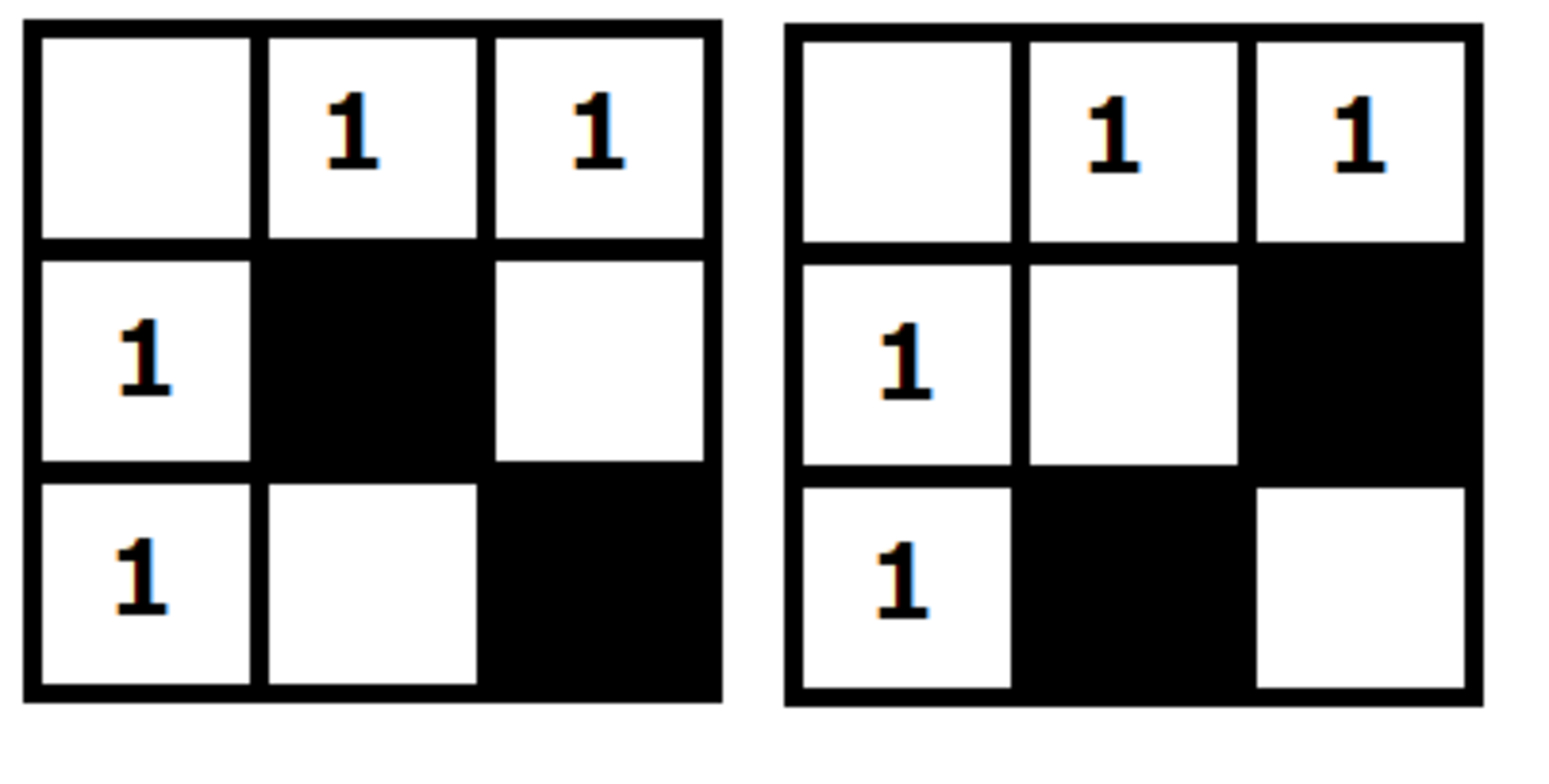 ピクロスの2つの解
ピクロスの2つの解
よって、最初の数字のヒントから絵がただ$1$通りに決まるというのは間違いです。
$$ピクロスの絵を以下のように定義する$$
$$A = \lbrace \begin{eqnarray}
\left(
\begin{array}{cc}
a_{11} & ・・・ & a_{1n} \\
・・・ & ・・・ & ・・・ \\
a_{n1} & ・・・ & a_{nn}
\end{array}
\right)
\end{eqnarray}, a_{ij} \in \lbrace 0,1 \rbrace, n,i,j \in \mathbb{N} \rbrace$$
$$0は塗りつぶさず、1は塗りつぶすことを意味する$$
$$ピクロスの絵から、絵を描く前に提示される最初の数字群を表すような写像を定義する$$
$$すなわち$$
$$f:A → R_{n[\frac{n+1}{2}]} × C_{[\frac{n+1}{2}]n}$$
$$fの像が、例えば$$
$f(\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 1 & 1 & 1 \\
0 & 0 & 0 & 0 & 0 \\
1 & 0 & 1 & 0 & 1 \\
0 & 1 & 0 & 1 & 1 \\
0 & 1 & 1 & 0 & 1 \\
\end{array}
\right)
\end{eqnarray})$
$= (\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 3 \\
0 & 0 & 0 \\
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 2 & 1 \\
\end{array}
\right)
\end{eqnarray}$ $,$$\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 0 & 1 & 0 & 0 \\
0 & 0 & 1 & 1 & 1\\
1 & 2 & 1 & 1 & 3\\
\end{array}
\right)
\end{eqnarray})$
$$となるように定義する$$
$$このとき$$
$f(\begin{eqnarray}
\left(
\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}
\right)
\end{eqnarray})
$ $=$ $= (\begin{eqnarray}
\left(
\begin{array}{cc}
1 \\
1
\end{array}
\right)
\end{eqnarray}$ $,$$\begin{eqnarray}
\left(
\begin{array}{cc}
1 & 1
\end{array}
\right)
\end{eqnarray})$
$$また$$
$f(\begin{eqnarray}
\left(
\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}
\right)
\end{eqnarray})
$ $=$ $= (\begin{eqnarray}
\left(
\begin{array}{cc}
1 \\
1
\end{array}
\right)
\end{eqnarray}$ $,$$\begin{eqnarray}
\left(
\begin{array}{cc}
1 & 1
\end{array}
\right)
\end{eqnarray})$
$$よって、fは単射ではない$$
$$これは、ピクロスで最初に与えられる数字群R_{n[\frac{n+1}{2}]} × C_{[\frac{n+1}{2}]n}に対し、解は1つではないことを表している$$
$$よって、ピクロスの解は1つに定まらない$$
※一般的な$A$の元に対しての$f$の移動先の値を数式で表すことができませんでしたが、ご了承ください。
