Fibonacci 数番目の Fibonacci 数を含む等式と無限和を構成してみる
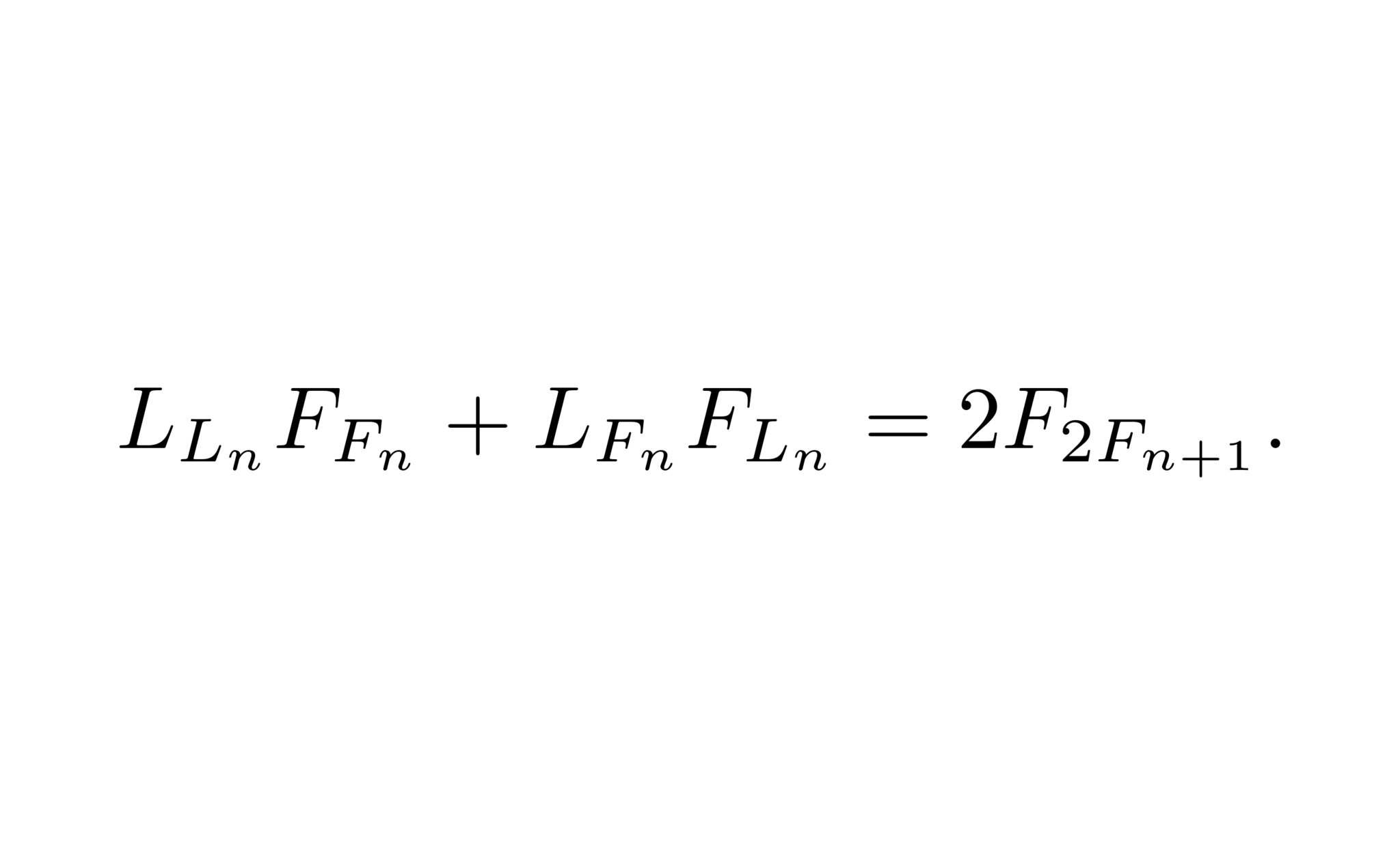Fibonacci 数番目の Fibonacci 数を含む等式
前提知識 : 数学的帰納法.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
始めに
お久振りです. ゆう の みぎうでです. この頃は Fibonacci 数を含む不定解析についての考察 (これについては非公開を原則としています) ばかりで, 余り紹介できる話題が無かったため記事を投稿していませんでした.
本稿においては, Fibonacci 数列 bot に登録している数式の中から幾つかの導出法を紹介します. これから扱う式は全て Fibonacci 数の番号の中に Fibonacci 数が入っているような形$F_{F_n}$を含むもので, 見た目の事も有ってきっと見ばえが好くなるのではないかなと期しております. 応用性は有りません.
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
基礎等式の準備
過去の記事と被っている内容が多いですが, 矢張り未だ Fibonacci 数の基礎等式の中には余り知られていないものが在り, ここでは一連の導出の流れを解説することにします. ここで扱う内容は本題ではないため, 証明は成るべく従来の記事と同様の手法を取るようにしています.
整数$i$を番号に有する二つの数列$(L_i)$と$(F_i)$を, これらの漸化式と初期値によって定義する.
\begin{align}
\left(
\begin{array}{l}
L_{i+2}=L_{i+1}+L_i,\quad L_0=2,\ L_1=1\\
F_{i+2}=F_{i+1}+F_i,\quad F_0=0,\ F_1=1
\end{array}
\right..
\end{align}
然らばこれらの数列は以下の表のようになることが計算によって確かめらます. これらの整数列には, それぞれ Lucas 数列, Fibonacci 数列という呼称が当られています.
\begin{align}
\begin{array}{c|ccccccc}
i&-3&-2&-1&0&1&2&3\\\hline
L_i&-4&3&-1&2&1&3&4\\
F_i&2&-1&1&0&1&1&2
\end{array}
\end{align}
\begin{align}
\begin{array}{c|cccccccc}
i&1&2&3&4&5&6&7&8\\\hline
L_i&1&3&4&7&11&18&29&47\\
F_i&1&1&2&3&5&8&13&21
\end{array}
\end{align}
線型の三項間漸化式によって定義される他の数列と同じく, これらの数列を観るに当っては, 漸化式の特性多項式である
\begin{align}
X^2-X-1
\end{align}
という二次式の根, 即ち二次方程式$X^2=X+1$の解が極めて重要です. この二次方程式の二つの解は無理数であるため, これらを一文字によって表せるように定義を布いておけば, 後の計算を簡明にすることができます.
二次方程式$X^2=X+1$の二つの無理数の解の内, 大きいほうを$\phi$, 小さいほうを$\bar\phi$によって表す. 即ち
\begin{align}
\phi=\frac{\,1+\sqrt{5}\,}{\,2\,},\quad\bar\phi=\frac{\,1-\sqrt{5}\,}{\,2\,}
\end{align}
である.
広く知られているようにこれらの内$\phi$のほうは黄金比という名で呼ばれており, 等式
\begin{align}
1+\phi=\phi^2
\end{align}
が成立することから, 等比数列
\begin{align}
(\phi^i)=1,\ \phi,\ \phi^2,\ \phi^3,\ \ldots
\end{align}
も Fibonacci 数と同一の漸化式$a_{i+2}=a_{i+1}+a_i$を有することになります. この漸化式の合致と, Lucas 数列および Fibonacci 数列の初期値が丁度の数として定義されていたことによって, 黄金比の累乗に関して単純明快なる等式を構成することができます.
如何なる整数$n$についても$\displaystyle\phi^n=\frac{\,L_n+F_n\sqrt{5}\,}{\,2\,}$である.
若しある整数$n$について, $n$と$n+1$のそれぞれに対応する等式
\begin{align}
\phi^n=\frac{\,L_n+F_n\sqrt{5}\,}{\,2\,},\quad\phi^{n+1}=\frac{\,L_{n+1}+F_{n+1}\sqrt{5}\,}{\,2\,}
\end{align}
の成立が正しいのであれば, これらの二本の等式を足しあわせることによって$n+2$に対応する等式が導かれ, また各辺の差を取ることによって$n-1$に対応する等式を得ることができる. 命題の等式は$n\in\{0,1\}$の場合においては明らかに成立しているため, 数学的帰納法によって証明が完せられる. $\quad\Box$
如何なる整数$n$についても$\displaystyle\bar\phi^n=\frac{\,L_n-F_n\sqrt{5}\,}{\,2\,}$である.
前の命題と同様なる帰納法によって証明される.
これらの等式を用いれば, 黄金比についての簡素な等式から, Lucas 数と Fibonacci 数の諸性質を導出することができます.
如何なる整数$n$についても, 等式
\begin{align}
L_{-n}=(-1)^nL_n,\quad F_{-n}=-(-1)^nF_n
\end{align}
が成立する.
等式$\phi^{-1}=-\bar\phi$の両辺を$n$乗して, 先の命題の二つの式を代入すると
\begin{align}
\frac{\,L_{-n}+F_{-n}\sqrt{5}\,}{\,2\,}=(-1)^n\frac{\,L_n-F_n\sqrt{5}\,}{\,2\,}
\end{align}
という等式が構成される. $\sqrt{5}$が無理数であることにより, 両辺の比較から命題の等式が導かれる. $\quad\Box$
如何なる整数$m,\ n$についても, 等式
\begin{align}
\left(
\begin{array}{l}
2L_{m+n}=L_mL_n+5F_mF_n\\
2F_{m+n}=L_mF_n+F_mL_n
\end{array}
\right.
\end{align}
が成立する.
指数法則の式$\phi^{m+n}=\phi^m\phi^n$に累乗の展開式を代入すると
\begin{align}
\frac{\,L_{m+n}+F_{m+n}\sqrt{5}\,}{\,2\,}&=\frac{\,L_m+F_m\sqrt{5}\,}{\,2\,}\frac{\,L_n+F_n\sqrt{5}\,}{\,2\,}\\
&=\frac{\,(L_mL_n+5F_mF_n)+(L_mF_n+F_mL_n)\sqrt{5}\,}{\,4\,}
\end{align}
という等式が構成される. $\sqrt{5}$が無理数であることにより, 両辺の比較から命題の等式が導かれる. $\quad\Box$
これを三角函数の加法定理
\begin{align}
\left(
\begin{array}{l}
\cos(x+y)=\cos{x}\cos{y}-\sin{x}\sin{y}\\
\sin(x+y)=\cos{x}\sin{y}+\sin{x}\cos{y}
\end{array}
\right.
\end{align}
に準えて捉えれば, 三角函数の積和等式
\begin{align}
\left(
\begin{array}{l}
\cos(x+y)+\cos(x-y)=2\cos{x}\cos{y}\\
\sin(x+y)+\sin(x-y)=2\sin{x}\cos{y}
\end{array}
\right.
\end{align}
に相当する等式を得ることができます.
如何なる整数$m,\ n$についても, 等式
\begin{align}
\left(
\begin{array}{l}
L_{m+n}+(-1)^nL_{m-n}=L_mL_n\\
F_{m+n}+(-1)^nF_{m-n}=F_mL_n
\end{array}
\right.
\end{align}
が成立する.
加法定理と符号の反転公式によって
\begin{align}
2L_{m+n}&=L_mL_n+5F_mF_n,\\
(-1)^n\cdot2L_{m-n}&=(-1)^n\left(L_mL_{-n}+5F_mF_{-m}\right)\\
&=L_mL_n-5F_mF_n
\end{align}
であることが判る. これら二式を足しあわせれば命題の第一の等式となる. この計算を Fibonacci 数列に置きかえてすれば第二の等式が同じくして得られる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
恒等式
ここから本題の恒等式と無限和について解説を書いてゆきます.
如何なる整数$n$についても, 等式
\begin{align}
L_{L_n}F_{F_n}+L_{F_n}F_{L_n}=2F_{2F_{n+1}}
\end{align}
が成立する.
左辺において加法定理を二度用いることによって
\begin{align}
L_{L_n}F_{F_n}+L_{F_n}F_{L_n}&=L_{L_n}F_{F_n}+F_{L_n}L_{F_n}\\
&=2F_{L_n+F_n}=2F_{L_nF_1+F_nL_1}\\
&=2F_{2F_{n+1}}
\end{align}
と計算することができる. $\quad\Box$
如何なる整数$n$においても$L_n$と$F_n$の偶奇は一致する.
差$L_n-F_n$が
\begin{align}
L_n-F_n=L_nF_{-1}+F_nL_{-1}=2F_{n-1}
\end{align}
と偶数になることから判る. $\quad\Box$
如何なる整数$n$についても, 等式
\begin{align}
L_{F_n}F_{L_n}-L_{L_n}F_{F_n}=2(-1)^{F_n}F_{2F_{n-1}}
\end{align}
が成立する.
左辺に$(-1)^{F_n}$を乗じたものは
\begin{align}
(-1)^{F_n}\left(L_{F_n}F_{L_n}-L_{L_n}F_{F_n}\right)&=L_{-F_n}F_{L_n}+L_{L_n}F_{-F_n}\\
&=L_{-F_n}F_{L_n}+F_{-F_n}L_{L_n}\\
&=2F_{-F_n+L_n}=2F_{L_{-1}F_n+F_{-1}L_n}\\
&=2F_{2F_{n-1}}
\end{align}
と計算することができ, この両辺を$(-1)^{F_n}$で割れば命題の式となる. $\quad\Box$
如何なる整数$n$についても, 等式
\begin{align}
L_{L_n}F_{L_n}+L_{F_n}F_{F_n}=L_{2F_{n-1}}F_{2F_{n+1}}
\end{align}
が成立する.
左辺において加法定理と積和等式を用いることによって
\begin{align}
L_{L_n}F_{L_n}+L_{F_n}F_{F_n}&=\frac{\,L_{L_n}F_{L_n}+F_{L_n}L_{L_n}\,}{\,2\,}+\frac{\,L_{F_n}F_{F_n}+F_{F_n}L_{F_n}\,}{\,2\,}\\
&=F_{2L_n}+F_{2F_n}\\
&=F_{(L_n+F_n)+(L_n-F_n)}+(-1)^{L_n-F_n}F_{(L_n+F_n)-(L_n-F_n)}\\
&=L_{L_n-F_n}F_{L_n+F_n}\\
&=L_{L_nF_{-1}+F_nL_{-1}}F_{L_nF_1+F_nL_1}\\
&=L_{2F_{n-1}}F_{2F_{n+1}}
\end{align}
と計算することができる. $\quad\Box$
如何なる整数$n$についても, 等式
\begin{align}
\left(
\begin{array}{l}
L_{L_{n+3}}=L_{L_{n+2}}L_{L_{n+1}}-(-1)^{L_{n+1}}L_{L_n}\\
L_{F_{n+3}}=L_{F_{n+2}}L_{F_{n+1}}-(-1)^{L_{n+1}}L_{F_n}
\end{array}
\right.
\end{align}
が成立する.
積和等式を適用すれば
\begin{align}
L_{L_{n+3}}+(-1)^{L_{n+1}}L_{L_n}&=L_{L_{n+2}+L_{n+1}}+(-1)^{L_{n+1}}L_{L_{n+2}-L_{n+1}}\\
&=L_{L_{n+2}}L_{L_{n+1}},\\
L_{F_{n+3}}+(-1)^{L_{n+1}}L_{F_n}&=L_{F_{n+2}+F_{n+1}}+(-1)^{F_{n+1}}L_{F_{n+2}-F_{n+1}}\\
&=L_{F_{n+2}}L_{F_{n+1}}.
\end{align}
と計算することができる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
無限和
極限$\displaystyle\lim_{n\to\infty}\frac{\,L_n\,}{\,F_n\,}$は$\sqrt{5}$に収束する.
$\phi^n=(L_n+F_n\sqrt{5})/2$と$\bar\phi^n=(L_n-F_n\sqrt{5})/2$の二本の式から
\begin{align}
L_n=\phi^n+\bar\phi^n,\quad F_n=\frac{\,\phi^n-\bar\phi^n\,}{\,\sqrt{5}\,}
\end{align}
という二つの数列の一般項が導かれる. これを代入すれば, $\bar\phi$の絶対値が$1$よりも小さいことにより
\begin{align}
\lim_{n\to\infty}\frac{\,L_n\,}{\,F_n\,}=\sqrt{5}\lim_{n\to\infty}\frac{\,\phi^n+\bar\phi^n\,}{\,\phi^n-\bar\phi^n\,}=\sqrt{5}
\end{align}
と極限値を得ることができる. $\quad\Box$
無限和$\displaystyle\sum_{n\geqslant1}(-1)^{F_n}\frac{\,F_{F_{n+1}}\,}{\,F_{F_n}F_{F_{n+2}}\,}$は$2\bar\phi$に収束する.
加法定理を用いれば
\begin{align}
\sum_{n\geqslant1}(-1)^{F_n}\frac{\,F_{F_{n+1}}\,}{\,F_{F_n}F_{F_{n+2}}\,}&=\sum_{n\geqslant1}(-1)^{F_n}\frac{\,F_{F_{n+2}-F_n}\,}{\,F_{F_n}F_{F_{n+2}}\,}\\
&=\frac{\,1\,}{\,2\,}\sum_{n\geqslant1}(-1)^{F_n}\frac{\,L_{F_{n+2}}F_{-F_n}+F_{F_{n+2}}L_{-F_n}\,}{\,F_{F_n}F_{F_{n+2}}\,}\\
&=\frac{\,1\,}{\,2\,}\sum_{n\geqslant1}\frac{\,-L_{F_{n+2}}F_{F_n}+F_{F_{n+2}}L_{F_n}\,}{\,F_{F_n}F_{F_{n+2}}\,}\\
&=\frac{\,1\,}{\,2\,}\sum_{n\geqslant1}\left(\frac{\,L_{F_n}\,}{\,F_{F_n}\,}-\frac{\,L_{F_{n+2}}\,}{\,F_{F_{n+2}}\,}\right)\\
&=\frac{\,1\,}{\,2\,}\left(\frac{\,L_{F_1}\,}{\,F_{F_1}\,}+\frac{\,L_{F_2}\,}{\,F_{F_2}\,}-\lim_{\ell\to\infty}\left(\frac{\,L_{F_{n+2}}\,}{\,F_{F_{n+2}}\,}+\frac{\,L_{F_{n+3}}\,}{\,F_{F_{n+3}}\,}\right)\right)\\
&=1-\sqrt{5}
\end{align}
という収束値が得られ, 黄金比の記号によっては$2\bar\phi$と書きかえられる. $\quad\Box$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
$\color{white}.\color{black}$
この記事を高評価した人
この記事に送られたバッジ
投稿者
