ガウス整数の商と余り(普通とは異なる定義)

この記事の目的

整数の除法で商と余りを求める方法には大きく分けて2通りある。
絶対値最小剰余 の除法と、 そうでない除法 である。

これは$ \mathbb{Z}[i] $の要素である ガウス整数の場合 に拡張することができる。
(この記事では$i$を虚数単位($i^2 = -1$)とする)

よく知られているのは$q$として、$\frac{a}{b} \in \mathbb{Q}[i]$に最も近い$q \in \mathbb{Z}[i]$を選ぶ( ガウス整数の余りつき割り算 )というものである。
これは絶対値最小剰余を拡張した除法といえる。
ただ、この除法は$a,b$の選び方によっては商$q$の決め方が何通りか考えられる。

「これをうまく解消できる除法を定義してみたい」、「絶対値最小剰余ではない除法を拡張できないだろうか？」というのがこの記事の目的である。
ただ先に結果を述べておくと、目的の達成はできてはいるがユークリッド互除法を行うためには工夫が必要になっている。

余りを構成する

$a,b \in \mathbb{Z}[i]$に対して$a / b$の余り$r$が、次の図1のように$b$と$ib$のつくる正方形の領域内に含まれるように定義する。

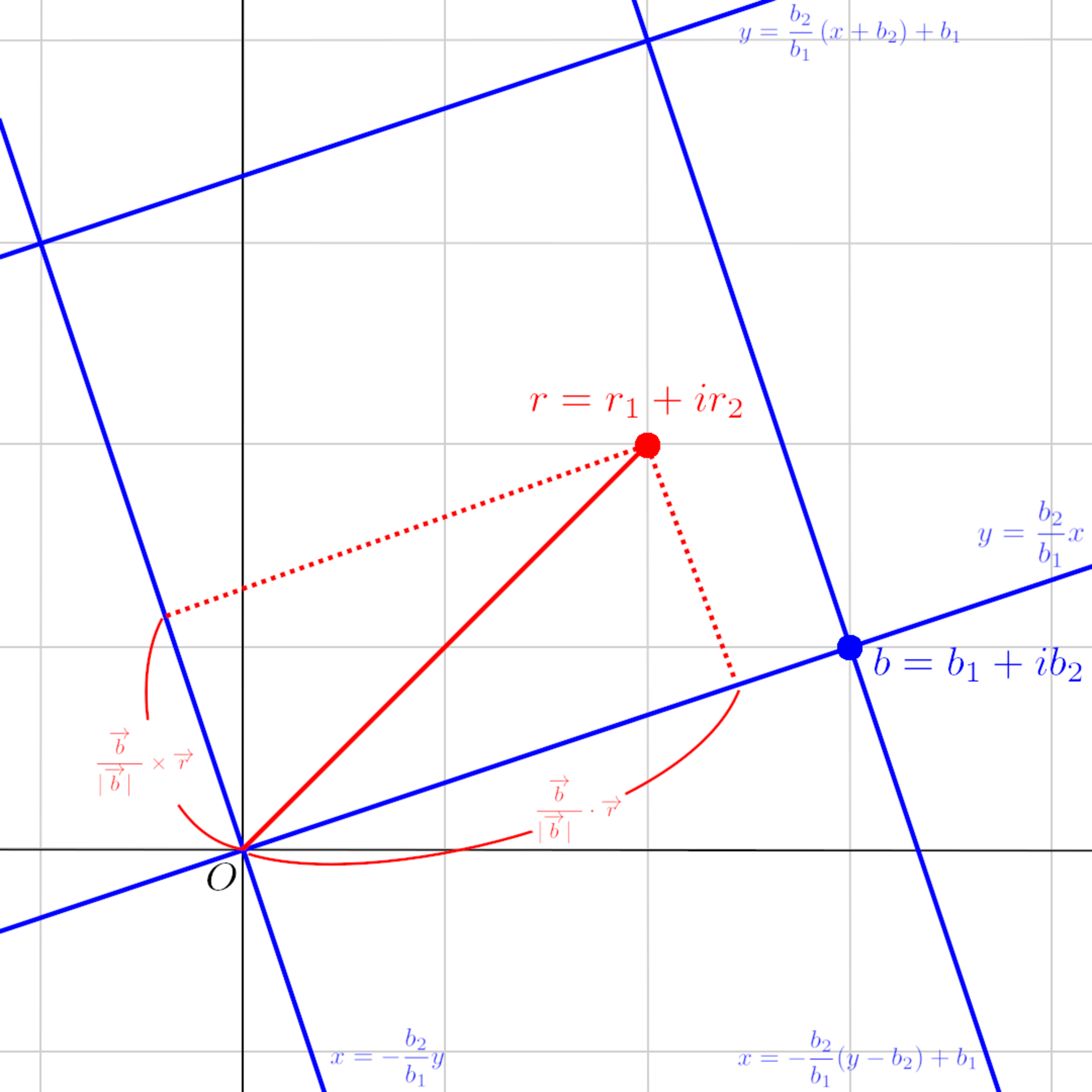除数と余りの関係

これはつまり、

が成り立つように、余り$r$を定義するということになる。

この記事では複素数$ a = a_1 + i a_2$に対応するベクトル$\overrightarrow{a} = (a_1, a_2)$を考え、
$$ \overrightarrow{a} \cdot \overrightarrow{b} = a_1 b_1 + a_2 b_2 $$
$$ \overrightarrow{a} \times \overrightarrow{b} = a_1 b_2 - a_2 b_1 $$
とする。

命題2が成り立つことは、単位ベクトルとの内積は正射影であるし、単位ベクトルとの二次元の外積は垂直方向への射影であることから分かる。

ここではこれを別の方法で示してみよう。

ここまでで、$b$と$ib$がつくる正方領域内に$r$が含まれる条件が分かった。
では、これをみたす商$q$と余り$r$はどのように計算したらよいのだろうか？

商と余りの計算方法

$$ \begin{eqnarray} \overline{b} r &=& (b_1 - i b_2)(r_1 + i r_2) \\ &=& (b_1 r_1 + b_2 r_2) + i (b_1 r_2 - b_2 r_1) \\ &=& \overrightarrow{b} \cdot \overrightarrow{r} + i \overrightarrow{b} \times \overrightarrow{r} \end{eqnarray} $$
であるため、$|b| = |\overrightarrow{b}|$に注意すると
$$ \frac{\overline{b}}{|b|^2} r = \frac{\overrightarrow{b}}{|\overrightarrow{b}|^2} \cdot \overrightarrow{r} + i \frac{\overrightarrow{b}}{|\overrightarrow{b}|^2} \times \overrightarrow{r} $$
であり、これはさらに
$$ b^{-1} r = Re(b^{-1} r) + i Im(b^{-1} r) $$
と表すことができる。

この結果と命題2から

が成り立つ。

では$a,b \in \mathbb{Z}[i]$において$a / b$の商$q$と余り$r$を計算方法はどうなるのだろうか。
$$ a = bq + r $$
$$ ab^{-1} = q + rb^{-1} $$
この実部と虚部はそれぞれ
$$ Re(ab^{-1})=Re(q)+Re(rb^{-1}) $$
$$ Im(ab^{-1})=Im(q)+Im(rb^{-1}) $$
である。
つまり$ab^{-1}$の実部と虚部を切り下げるだけで、商$q$が得られる。
$r$は$r = a - bq$により計算できる。

これらをまとめる前に記号を定義する。
記号$\lfloor \, \rfloor$で 床関数 を表すことにする。
ここでは床関数を拡張して

とする。

以上から次のことが結論付けられた。

このように ドナルド・クヌースの「切り下げ除算」 はガウス整数にそのまま拡張できる。
この除法は、「除数$b$が作る正方領域内に余り$r$が含まれる」という幾何学的側面とも関係し、大変興味深い。

ユークリッド互除法の適用法

ではユークリッド互除法は成り立つのだろうか。
残念ながら普通には計算できない。
しかし、工夫することで互除法を使うことができる。

まずは、なぜそのままでは使うことができないのかを考えよう。

命題3より
$$ 0 \leq Re(rb^{-1})^2 + Im(rb^{-1})^2 < 2 $$
$$ 0 \leq \frac{|r|^2}{|b|^2} < 2 $$
$$ 0 \leq |r| < \sqrt{2} |b| $$
は常に成り立つが、$|r| < |b|$は$a,b$の選び方によっては成り立たないこともある。
(例えば$a=5+4i,b=3+i$のとき$q=1,r=2+3i$のため$|b|<|r|$)
そのため互除法をそのまま使うことはできない。
($a=53-16i,b=59+6i$の場合は、互除法をそのまま使うと計算が無限に続いてしまう)

ここで少し思い起こしてみると、自然数$a,b$の最大公約数$gcd(a,b)$を求めるユークリッド互除法では
$$ gcd(a,b)=gcd(b,r) $$
という性質を利用して計算した。
ただし$0 \leq r < b$であり、これが互除法の計算が終わる上で大切だった。

そのため、これをガウス整数に適用する場合は
$$ gcd(a,b) = \begin{eqnarray} \left\{ \begin{array}{l} gcd(b, r) ~~~~~~~~~~~\, (|r| < |b|) \\ gcd(b, r-b) ~~~~~ (|b|\leq|r|,|r-b|\leq|r-ib|) \\ gcd(b, r-ib) ~~~~ (|b|\leq|r|,|r-ib|<|r-b|) \end{array} \right. \end{eqnarray} $$
のように工夫が必要になる。

どうしてこの工夫で互除法の計算が上手く進むのだろう。

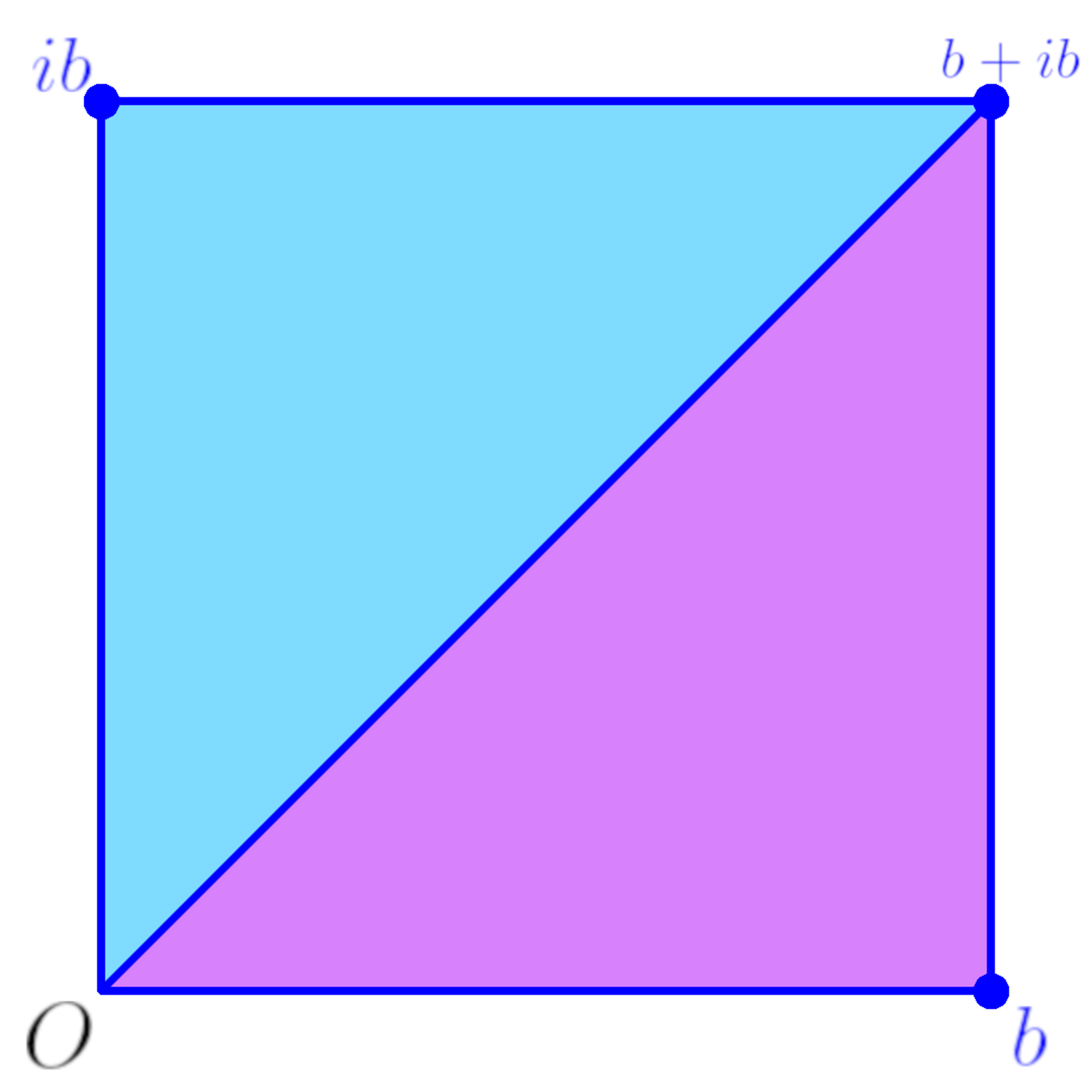ユークリッド互除法の調整

$r$が図2の紫色の領域にあり、しかも例えば$|b|<|r|$の位置にある場合、$b$と$b+ib$の距離は$|b|$であるため$|r-b| < |(b+ib) - b| = |b|$となる(紫色の領域内で$b$から一番遠いのは原点か$b+ib$だから)。そのため$gcd(b, r-b)$とすれば互除法を続けることができるからである。
(水色の領域に$r$がある場合も同様)

まとめ

商と余りを一意に定められる除法を構成でき、計算方法もシンプルであるのは興味深い。
一方でユークリッド互除法を適用するために工夫が必要となるのは惜しい結果だった。