ゆうすい模試(極限)の解説
はじめに
この記事では, ゆうすい模試 の解説をしようと思います. 解答例とともに, 考え方や, 講評的なものも書いてみようと思います. 解いてくださった方々, ありがとうございました.
第1問, 第2問は簡単なので要点の説明だけにし, 第3問以降はきちんとした解答例を挙げました. これらの$\TeX$打ちを手伝ってくださったNRSKさんに感謝申し上げます.
${}$
第1問
$\Delta ABC$は $AB=1+x,\ BC=2+x,\ CA=3+x$ を満たすとする. 以下の極限を求めよ.
\begin{align*}\ds (1)& \lim_{x\to+0}\ \frac{\sin\angle A}{\sin\angle C}\quad &(2)& \lim_{x\to+0}\ \frac{\angle A}{\angle C}\quad &(3)& \lim_{x\to2}\ \frac{\angle B-\frac\pi2\ }{x-2} & \end{align*}
これはまあ, 計算するだけですかね... (2)はだいたい対辺の比に等しくて$2$くらいかなって予想できるかもしれません. (3)はなんか計算ミスしてる方が多かったです.
ということで, (1)は正弦定理使って, (2)は $\dfrac{\sin\angle A}{\angle A}\to1$ を使って, (3)は流れからして$\sin(\angle B-\tfrac\pi2)$を考えれば良いので, 余弦定理とか使えば良いです. 簡単でしたね. 一応答えは$2,2,-\frac16$となります.
${}$
第2問
(1) $0< x<1$とする. $0\leqq t\leqq x$ のとき $(1-x)t\leqq \sin t\leqq t $ が成り立つことを示せ.
(2) $0\leqq t\leqq x$ のとき $\ds (1-x)^2\leqq \frac{x^2+\sin^2t}{x^2+t^2}\leqq 1$ が成り立つことを示せ.
(3) $\ds\lim_{x\to+0}\ \int_0^x\frac{x}{x^2+\sin^2t}\,dt$ を求めよ.
初めは(3)だけで出そうと思ったのですが, さすがにあれかなと思って, 入試問題的な誘導をつけてみました. まあ誘導は面倒なだけなのでどう示しても結構です. ほとんどの方が出来ていました. 長いのでここには書きません.
お気持ちとしては, 積分区間がとても小さくなるので, だいたい$\sin t\approx t$とできて, 積分もだいたい $\ds\int_0^x\frac{x}{x^2+t^2}\,dt=\frac\pi4$ くらいになるということでした. (ただし極限と積分の入れ替えは一般には出来ないので, 厳密には面倒な評価が必要になります.)
${}$
第3問
$n$を自然数とする. $x$の方程式
$$\sin x+\sin 2x+\cdots +\sin nx\ =\ 1$$
の正の解のうち最小のものを$x_n$とするとき, $\ds\lim_{n\to\infty} n^2x_n$ を求めよ.
これは, 近似が分かっていれば簡単に予測できる問題でした. だいたい$\sin x\approx x$なので$(1+\cdots n)x_n\approx1$で, $x_n\approx\dfrac2{n(n+1)}$くらいなので, 答は$2$ですよね.
具体的な解法としては, ひとつには左辺の和を明示する方法があります. これは多くの方がやってらして, 実際割と簡単に行きます. でもこの方法は汎用性がないので, ここでは不等式評価を利用したいと思います.
$\sin x$は上からは$x$で押さえられますが, 下から$1$次式で押さえるには割線近似が必要です. それらを駆使すると, 例えば以下のようになります.
[解答例]
左辺を$f(x)$とする.まず$\sin{x}< x$を使うと,$1=f(x_n)<(1+2+\cdots+n)x_n$より,$\displaystyle\frac{2}{n(n+1)}< x_n$を得る.
次に$x_n$の上からの評価だが,$\sin{x}$の上凸性より,$\displaystyle 0< x<\frac{\pi}{2}$で$\displaystyle\sin{x}>\frac{2}{\pi}x$を用いると,$\displaystyle f\left(\frac{\pi}{n^2}\right)>\frac{2}{\pi}\cdot\frac{\pi}{n^2}\cdot\frac{1}{2}n(n+1)>1$
これと$f(0)=0<1$から,中間値の定理で$\displaystyle x_n<\frac{\pi}{n^2}$である. これでは評価が甘いのでもう1度押さえる.
再度$\sin{x}$の上凸性より$\displaystyle 0< x<\frac{\pi}{n}$で$\displaystyle\sin{x}>\frac{\sin{\frac{\pi}{n}}}{\frac{\pi}{n}}x$を用いると,$\displaystyle1=f(x_n)>\frac{\sin{\frac{\pi}{n}}}{\frac{\pi}{n}}\cdot(1+2+\cdots+n)x_n$を得る.
以上より,
$$\displaystyle\frac{2n}{n+1}< n^2x_n<\frac{\frac{\pi}{n}}{\sin{\frac{\pi}{n}}}\cdot\frac{2n}{n+1}$$
なので,$n\to\infty$としてはさみうちの原理より$\displaystyle\lim_{n\to\infty}n^2x_n=2$である. □
${}$
第4問
$n$を自然数とする. $x$の方程式 $x^3+n^2x-n^2=0$ は$1$つの実数解と$2$つの虚数解を持つので, それらを $a_n,\ b_n+c_ni,\ b_n-c_ni$ とおく(ただし$a_n,b_n,c_n$は実数で$c_n>0$). 以下の極限を求めよ.
\begin{align*}\ds (1)& \lim_{n\to\infty}a_n\hspace{60pt} &(2)& \lim_{n\to\infty}b_n\hspace{60pt} &(3)& \lim_{n\to\infty}\frac{c_n}{n} \end{align*}
$(4) \ (3)$の値を$p$として, $\ds\lim_{n\to\infty}\ n(c_n-pn)$
これは少し目新しい感じかもしれません. でも, 解と係数の関係を使うことさえ分かれば特に難しいことなく最後まで楽しく解けるのではないかと思います. この問題は私のお気に入りです. あまり発想は必要ないですかね. ((1)の示し方は色々なやり方があるかもしれません)
[解答例]
(1)左辺を$f(x)$とすると$f(0)<0,f(1)>0$より中間値の定理から$0< a_n<1$であることに注意して,
$$f(a_n)=a_n^3+n^2a_n-n^2=0\qquad \mathrm{i.e}\qquad \displaystyle a_n=1-\frac{{a_n}^3}{n^2}$$
で$n\to\infty$として$\displaystyle\lim_{n\to\infty}a_n=1$である.
(2)解と係数の関係より,
$$ \begin{eqnarray}
\left\{
\begin{array}{l}
a_n+2b_n=0\quad &\cdots (A)\\
2a_nb_n+{b_n}^2+{c_n}^2=n^2\quad&\cdots(B) \\
a_n({b_n}^2+c_n^2)=n^2\quad&\cdots(C)
\end{array}
\right.
\end{eqnarray} $$
であることに注意する.
$(A)$より,$\displaystyle b_n=-\frac{1}{2}a_n$だから,$\displaystyle\lim_{n\to\infty}b_n=-\frac{1}{2}$である.
(3)$(B)$と$c_n>0$より,$\displaystyle\frac{c_n}{n}=\sqrt{1-\frac{2a_nb_n+b_n^2}{n^2}}$だから,$\displaystyle\lim_{n\to\infty}\frac{c_n}{n}=1$である.
(4)$(B)$より,$\displaystyle n(c_n-n)=-n\cdot\frac{2a_nb_n+b_n^2}{c_n+n}=-\frac{2a_nb_n+b_n^2}{1+\frac{c_n}{n}}$だから,$\displaystyle\lim_{n\to\infty}n(c_n-n)=-\frac{2\cdot1\cdot(-\frac{1}{2})+(-\frac{1}{2})^2}{1+1}=\frac{3}{8}$である. □
${}$
第5問
$r$を$1$より大きい実数とする. $xy$平面において$A(0,1)$とし, 動点$P,Q$は, $A$が線分$PQ$上にあってかつ$PQ=r$を満たすとする. $P$が点$(-\sqrt{r^2-1},0)$から点$(\sqrt{r^2-1},0)$まで$x$軸上を動くときの$Q$の軌跡が囲む領域の面積を$S(r)$とするとき, $\ds\lim_{r\to\infty}\frac{S(r)}{r^2}$ を求めよ.
これは, 大半の方が$S(r)$を真面目に計算されていました. そして私はそれを見てほくそ笑んでおりました.() というのも実は, 答を予測するのにも, 厳密な評価にも, $S(r)$どころか$Q$の軌跡すら必要ないからです.
まずは予想の仕方としては, 図形全体を$1/r$倍すると分かりやすいと思います. 即ち, $PQ=1, A(0,1/r)$としてみます. すると$Q$の軌跡はほとんど半円に近いことが分かります. なので答は$\dhp$です. 厳密な評価は, 適当な扇形によって外側と内側から押さえてやれば良いです.
[解答例]
題意の領域を$W_r$と置く.まず,$AQ\leq r-1$なので,$W_r$は原点中心半径$r$の上半円に含まれる.従って,$\displaystyle S(r)<\frac{\pi}{2}r^2$である.
次に,$P$が$(-\sqrt{r^2-1},0)$から$(0,0)$まで動く間に$AQ$の長さと傾きは単調増加することから,$Q$の軌跡上に$y$軸対称な2点$R,R'$を取った時,中心$A$半径$AR$の扇形$ARR'$は$W_r$に含まれる.ここで$R$を,$P=(-\sqrt{r},0)$の時の$Q$とすると,$AR=r-\sqrt{1+r}$であり,扇形$ARR'$の中心角は$\displaystyle\tan{\theta_r}=\sqrt{r},0<\theta_r<\frac{\pi}{2}$となる$\theta_r$を用いて,$\displaystyle 2\theta_r$である.従って,$ \displaystyle S(r)>\frac{1}{2}(r-\sqrt{1+r})^2\cdot 2\theta_r$である.
$\displaystyle\lim_{r\to\infty}\theta_r=\frac{\pi}{2}$に注意して, はさみうちの原理より,$\displaystyle\lim_{r\to\infty}\frac{S(r)}{r^2}=\frac{\pi}{2}$である. □
下図の赤線は$r=30$のときの$Q$の軌跡である.
 問5
問5
${}$
第6問
$n$を自然数とする. 実数$x$に対し, $x$以下の最大の整数を$[x]$と表すことにする. 以下で, 円周率$\pi$は$3.14<\pi<3.15$を満たす無理数であることを用いて良い.
(1) $\ds\left[\frac{k}{\pi}\right]=\left[\frac{k+3}{\pi}\right],\ 0\leqq k\leqq n$ を満たす整数$k$の個数を$a_n$とおく. $\ds\lim_{n\to\infty}\frac{a_n}{n}$ を求めよ.
(2) $\ds\left[\frac{k}{\pi}\right]+3=\left[\frac{k+7}{\pi}\right],\ 0\leqq k\leqq n$ を満たす整数$k$の個数を$b_n$とおく. $\ds\lim_{n\to\infty}\frac{b_n}{n}$ を求めよ.
これは, 厳密にやろうと思うとすると結構技巧的な方法が必要となります(厳密な証明を送って下さった方は数名でした)が, 予想だけなら, 確率みたいな考えをすれば簡単に出来ますね.
即ち, $\ds\left[\frac{k}{\pi}\right]=\left[\frac{k}{\pi}+\frac{3}{\pi}\right]$を満たすのは$\dfrac{k}{\pi}$の小数部分が$1-\dfrac{3}{\pi}$未満のときであって, $\dfrac{k}{\pi}$の小数部分はほとんど$0$から$1$のランダムな値をとるので, 確率的に考えれば答も$1-\dfrac{3}{\pi}$になる, というものです.
厳密な方法としては, こういう整数部分をとる系のやつは, 各$k$に対して$\ds\left[\frac{k}{\pi}\right]$を考えるだけでなく, 各$m$に対して$\ds m=\left[\frac{k}{\pi}\right]$なる$k$の個数を考える, つまり数える方向を変えると上手くいくことが多いです. 下図のようにグラフにすると分かりやすいです.(横軸が$k$で, 直線の下の正方形の$y$座標が$[k/\pi]$に対応)
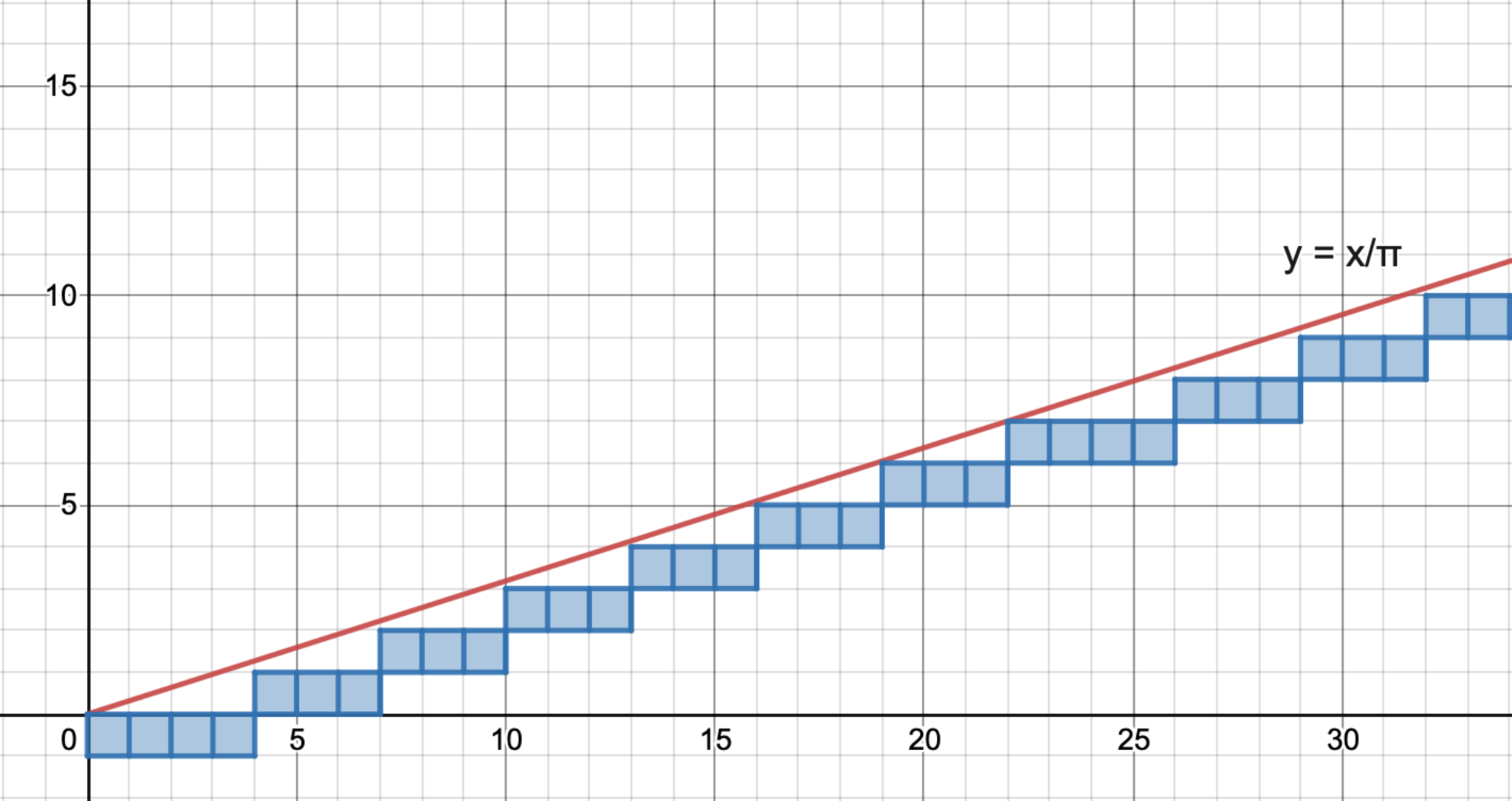 問6
問6
[解答例]
(1)整数$m$に対し$\displaystyle\left[\frac{k}{\pi}\right]=m$なる$k$の個数を$f(m)$とおくと, この値は$3$か$4$に限られる.$\displaystyle m=0,1\cdots,\left[\frac{n}{\pi}\right]$のうちで$f(m)=3$なる$m$を$N_3$個,$f(m)=4$なる$m$を$N_4$個とすると,$a_n=N_4$である.
まず,$m$の総数から
$$\displaystyle N_3+N_4=\left[\frac{n}{\pi}\right]+1\,\,\,\cdots(A)$$
が成立する.さらに$k$の総数から
$$ n\leq 3N_3+4N_4\leq n+3\,\,\,\cdots(B)$$
が成立する.($\displaystyle m=\left[\frac{n}{\pi}\right]$の時のみ,$\displaystyle \left[\frac{k}{\pi}\right]$になる$k$は$n$より大きくなり得るので,その分を不等式で評価した)
$(B)-3(A)$より,
$$\displaystyle 1-\frac{3}{n}\left[\frac{n}{\pi}\right]-\frac{3}{n}\leq\frac{N_4}{n}\leq1-\frac{3}{n}\left[\frac{n}{\pi}\right]$$
だから,$\displaystyle\lim_{n\to\infty}\frac{a_n}{n}=1-\frac{3}{\pi}$である.
(2)今度は組$(f(m),f(m+1))$を考えると,$\pi<3.5$より,これは$(4,4)$とはなり得ないことが分かる.
$\displaystyle m=0,1\cdots,\left[\frac{n}{\pi}\right]$のうち,これが$(3,3)$となる$m$を$N_{33}$個,$(3,4)$となる$m$を$N_{34}$個,$(4,3)$となる$m$を$N_{43}$個とすると,$b_n=N_{33}$である.
まず$m$の総数から
$$\displaystyle N_{33}+N_{34}+N_{43}=\left[\frac{n}{\pi}\right]+1\,\,\,\cdots(C)$$
次に,$N_{43}$は$f(m)=4$なる$m$の個数に等しいから,$N_{43}=N_4\,\,\,\cdots(D)$である.$N_{34}$についても同様だが,$f(0)=4$をカウントしないことと,$f(m+1)=4$になる可能性を加味して,$N_4-1\leq N_{34}\leq N_4\cdots(E)$が成立する.$(C),(D),(E)$より,
$$\displaystyle\frac{1}{n}\left[\frac{n}{\pi}\right]-2\frac{N_4}{n}+\frac{1}{n}\leq\frac{N_{33}}{n}\leq\frac{1}{n}\left[\frac{n}{\pi}\right]-2\frac{N_{4}}{n}+\frac{2}{n}$$
だから,$\displaystyle\lim_{n\to\infty}\frac{b_n}{n}=\frac{1}{\pi}-2\left(1-\frac{3}{\pi}\right)=\frac{7}{\pi}-2$である.
${}$
最後に
まずは, ここまで読んでくださった方, 本当にありがとうございました. 楽しんでいただけたでしょうか.
やはり極限は, 第3問や第5問のような問題を感覚的に近似して予想するのが楽しいですね. また, 今回はほとんどがそうでしたが, $a_n$とか$x_n$の具体的な値はひとつも求まらないのに極限値だけは求まるというのも不思議で面白いですよね. (ですから第5問で$S(r)$を具体的に求めるのは邪道なのです!)
また気が向いたら高校数学の作問を作ろうと思います. 今回は私も十分に楽しませていただきました. それでは, ありがとうございました.
${}$
