Fibonacci数と組み合わせ論
はじめに
本稿では,漸化式$F_1=1, F_2=1, F_{n+2}=F_{n+1}+F_{n}\quad(n=1, 2,\cdots)$で与えられるFibonacci数について,その華麗な性質のいくつかを,問題を通して組み合わせ論的な側面から眺めてみます.
なお,本稿では上記のように,$n$番目のFibonacci数を$F_n$で表すものとします.
問題をいくつか
$n$段$(n\geq1)$の階段がある.一歩で$1$段か$2$段登るとき,登り方の総数は何通りか.
例えば$n=4$のとき,以下の5通りである.
![問題1 !FORMULA[8][36584035][0]の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20210831160948.jpg?alt=media) 問題1 $n=4$の例
問題1 $n=4$の例
一列に並んだ$n$個のマスを,白が連続しないように白と黒で塗り分ける方法は何通りか.
例えば$n=3$のとき,以下の5通りである.
![問題2 !FORMULA[11][36584004][0]の例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20210831161532.jpg?alt=media) 問題2 $n=3$の例
問題2 $n=3$の例
それでは解答を書いていきます.考えたい人は考えてください.(答え自体は容易に想像つくけど……)
問題1の解答
■$n=1, 2$のとき
このとき,それぞれ1通り,2通り.
■$n\geq3$のとき
最後の一歩として,「$n-1$段目から$1$段登る」か「$n-2$段目から$2$段登る」の$2$通りが考えられる.よって求める登り方の通り数は($n-1$段の通り数)$+$($n-2$段の通り数).
以上より,$F_{n+1}$通りが求める答えである.
問題2の解答
問題1の階段で,$n+1$段のものを考える.
この階段の$1$段目から$n$段目までをマス目とみなし,段を踏んで登ることをマスを黒く塗ることを$1$対$1$に対応付けることが出来る.
以上より,$F_{n+2}$通りが求める答えである.
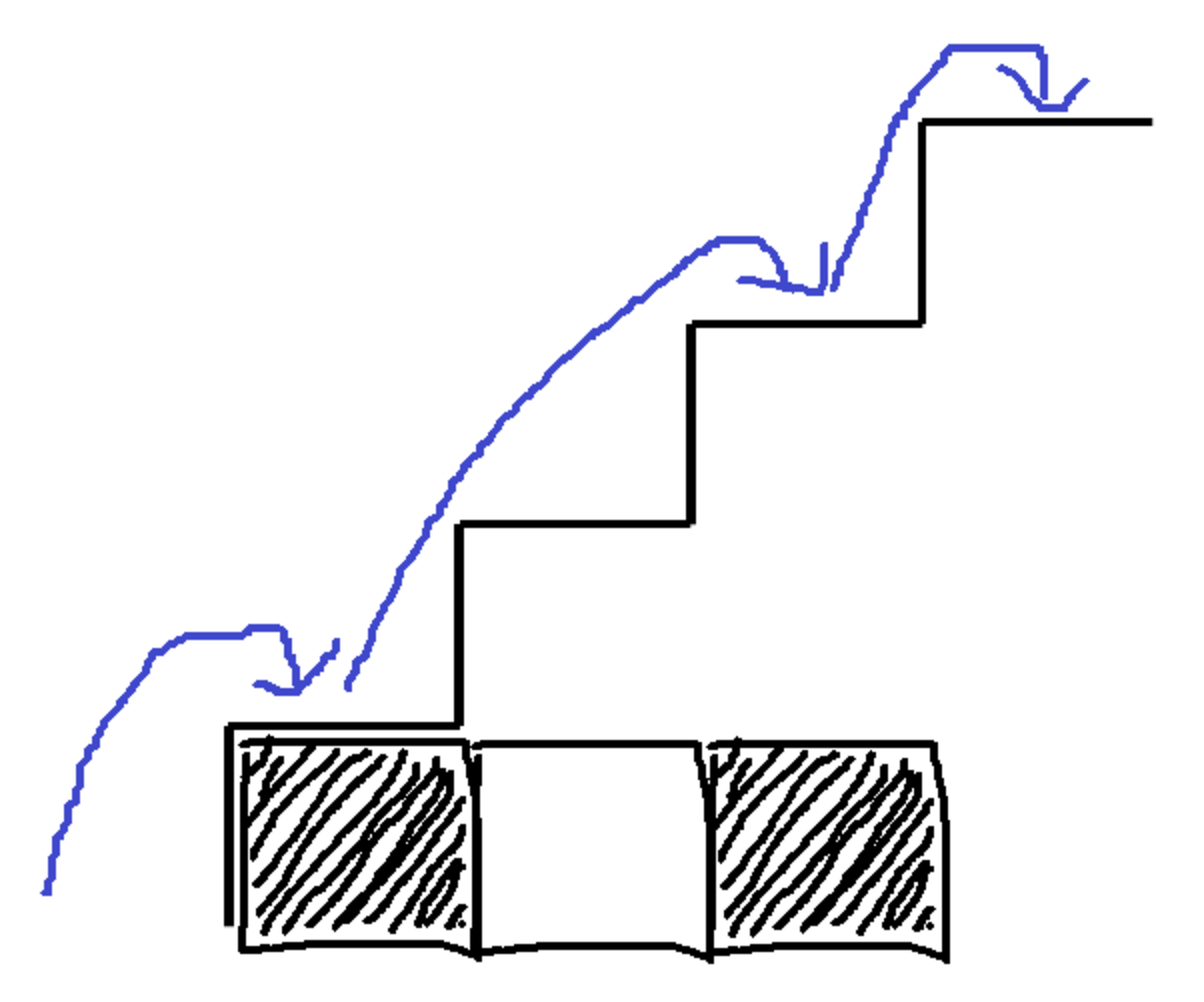 1対1対応
1対1対応
問題1,問題2を踏まえて,これらは次のように一般化することができる.
正の整数$n$を順序も含めて$1$と$2$の和に分ける方法は$F_{n+1}$通りである.
さらに,これから他にも次のような系も考えることができる.
縦$2$マス,横$n$マスのマス目を,$1\times2$のタイルで敷き詰める方法は$F_{n+1}$通りである.
拡張してみよう
問題1の拡張
まずは問題1を拡げてみる.問題1を再掲しておこう.
$n$段$(n\geq1)$の階段がある.一歩で$1$段か$2$段登るとき,登り方の総数は何通りか.
$m+n$段の階段を考える.問題1の解答を用いてこれの登り方の通り数を求める.
まず,問題$1$の解答より,登り方の通り数は$F_{m+n+1}$通り.
さて,次に,登り方には$m$段目を踏むか$m$段目を踏まないの$2$通りがあることを考える.
前者は($m$段の登り方)$\times$($n-1$段の登り方)通り,後者は($m-1$段の登り方)$\times$($n$段の登り方)通りである.
以上より,次がいえる:
$$F_{m+n+1}=F_{m+1}F_{n+1}+F_{m}F_{n}$$
添字を書き換えて,
$$F_{m+n}=F_{m+1}F_{n}+F_{m}F_{n-1}$$
これは加法定理と呼ばれる.
これはよくFibonacci数列の一般項を表すBinetの公式を用いて示されることが多いが,このような組み合わせ論的な証明を見出すことができた.
また,この加法定理については こちらの記事 もぜひご覧ください.
問題2の拡張
次に問題2について.これも再掲しておく.
一列に並んだ$n$個のマスを,\textbf{白が連続しないように}白と黒で塗り分ける方法は何通りか.
$n$個のマスのうち,$k$個を白で塗ることを考えよう.
このときの塗り方は,黒マスを$n-k$個用意し,その両端と間の$n-k+1$か所の中から白マスが入るところを選ぶ場合の数に等しいので${}_{n-k+1}\mathrm{C}_{k}$通り.
■$n=5, k=2$のとき
下図より,${}_{4}\mathrm{C}_{2}$通り.
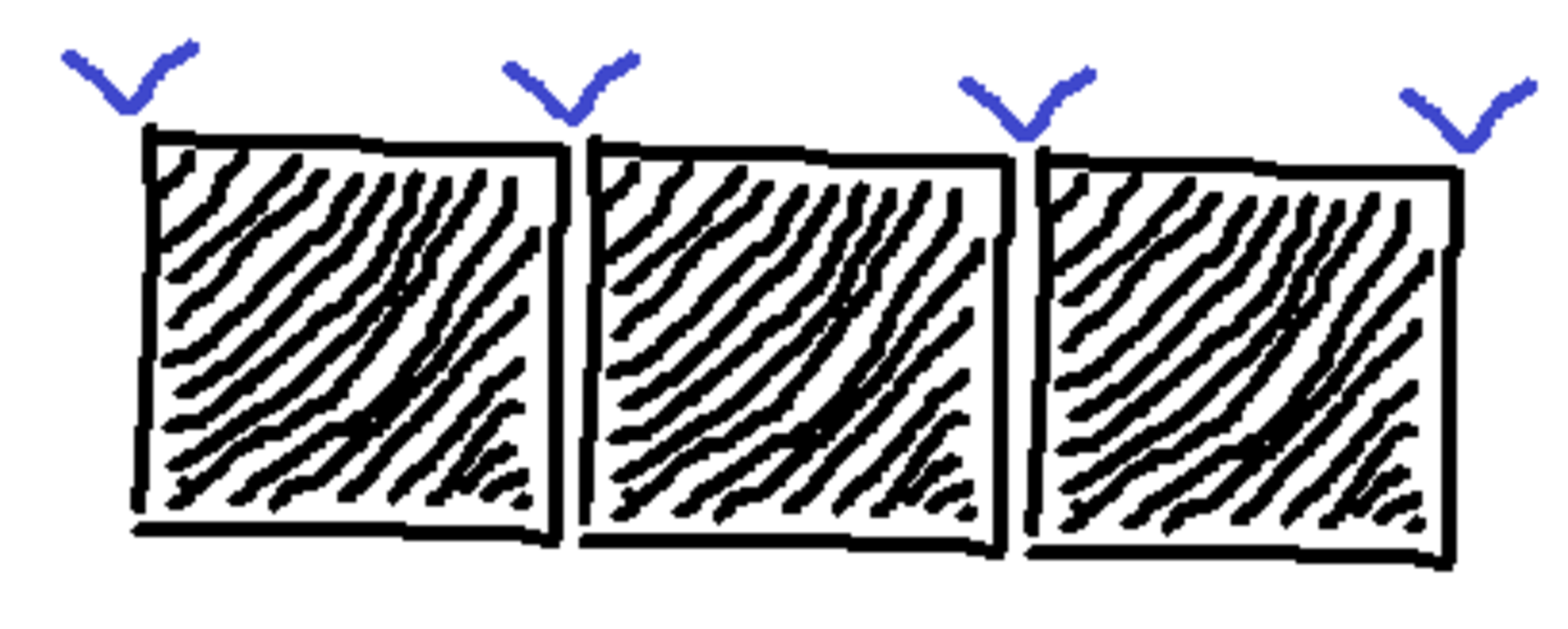 例
例
ここで,$k$は$0$から$\left\lfloor\dfrac{n+1}{2}\right\rfloor$までの値をとることから,次を得る:
$$F_{n+2}=\sum_{k=0}^{\left\lfloor(n+1)/2\right\rfloor}{}_{n-k+1}\mathrm{C}_{k}$$
添字を書き換えて,
$$F_{n+1}=\sum_{k=0}^{\left\lfloor n/2\right\rfloor}{}_{n-k}\mathrm{C}_{k}$$
が成り立つ.
ここからさらに,Pascalの三角形を考えよう.
 Pascalの三角形
Pascalの三角形
これは,次に示す補題2から,二項係数を用いて次のように書くことができる:
 Pascalの三角形
Pascalの三角形
$${}_{n+1}\mathrm{C}_{k}={}_{n}\mathrm{C}_{k-1}+{}_{n}\mathrm{C}_{k}$$
\begin{eqnarray*} & &{}_{n}\mathrm{C}_{k-1}+{}_{n}\mathrm{C}_{k}\\&=&\dfrac{n!}{(k-1)!(n-k+1)!}+\dfrac{n!}{k!(n-k)!}\\&=&\dfrac{k\cdot n!+(n-k+1)\cdot n!}{k!(n-k+1)!}\\&=&\dfrac{(n+1)!}{k!(n-k+1)!}\\&=&{}_{n+1}\mathrm{C}_{k}\end{eqnarray*}
さて,先ほど得た$F_{n+1}=\sum_{k=0}^{\left\lfloor n/2\right\rfloor}{}_{n-k}\mathrm{C}_{k}$の式について考えよう.右辺の二項係数の和の部分は,Pascalの三角形では直線上に現れる.例えば,$n=4$のときは下図のところに現れ,これらの和が$F_4$になっている.
 Pascalの三角形
Pascalの三角形
以上のことより,Pascalの三角形を下図のように斜めに足すと,Fibonacci数列が現れる.
 Pascalの三角形
Pascalの三角形
