文献あり

柔軟に解く図形問題　〜哲学の深淵にピザは宿る〜

535

　本記事では匿の自作問題のひとつを紹介する。様々な要素を1題に凝縮したオムニバスな問題であるため、解説を見る前に、どうか暫く考えてもらいたい。
　なお、本記事の副題である『哲学の深淵にピザは宿る』に深い意味は無く、ただ Twitter で「タイトルに使えそうな単語」を募集した結果集まったものを抽選して組み合わせただけである。
　他にも「煩悩」・「カルボナーラ」・「筋肉」などの秀逸な案を紹介してもらった。この場を借りて感謝を申し上げる。

問題

△ A B C

において、傍心を

J

、傍接円を

ω

とし、

ω

と

B C

の接点を

D

とする。
　線分

A D

の四等分点を点

A

に近い順で

P, Q, R

と、

A D

と垂直な

ω

の直径の両端を直線

A B

に近い順で

E, F

と、それぞれ名付ける。
　

D E

と

F Q

の交点を

K

、

B Q

と

K R

の交点を

L

としたとき、直線

J L

上に線分

B K

の中点

M

が存在することを示せ。

　余談だが、問題を解く際に

A B = 5, B C = 6, C A = 7

として作図すると綺麗な図を描ける。

解説

　まず、以下の補題が成立することを明記しておく。これらが成立することの証明は割愛するので、もし証明を知りたければ高校数学の美しい物語 - 調和点列の様々な定義と具体例を参照されたい。

　円

c

の外部の点

P

から

c

に接線を引き、接線と

c

の接点を

T_{1}, T_{2}

とする。点

P

を通り

c

と2回交わる直線

l

について、

l

と

c

の交点を点

P

に近い順で

I_{1}, I_{2}

、

l

と

T_{1} T_{2}

の交点を

T

としたとき、

P I_{1} : I_{1} T = P I_{2} : I_{2} T

が成立する。(このような性質が成り立つとき、

{P, I_{1}, T, I_{2}}

は調和点列であるという。)

　補題1で与えた図に関して、線分

I_{1} I_{2}

の中点を

M

としたとき、

I_{1} M^{2} = I_{2} M^{2} = P M \times T M

が成立する。

　補題の確認が済んだところで、手を動かしてみよう。問題文に即して図を描くと、図1左側のようになる。

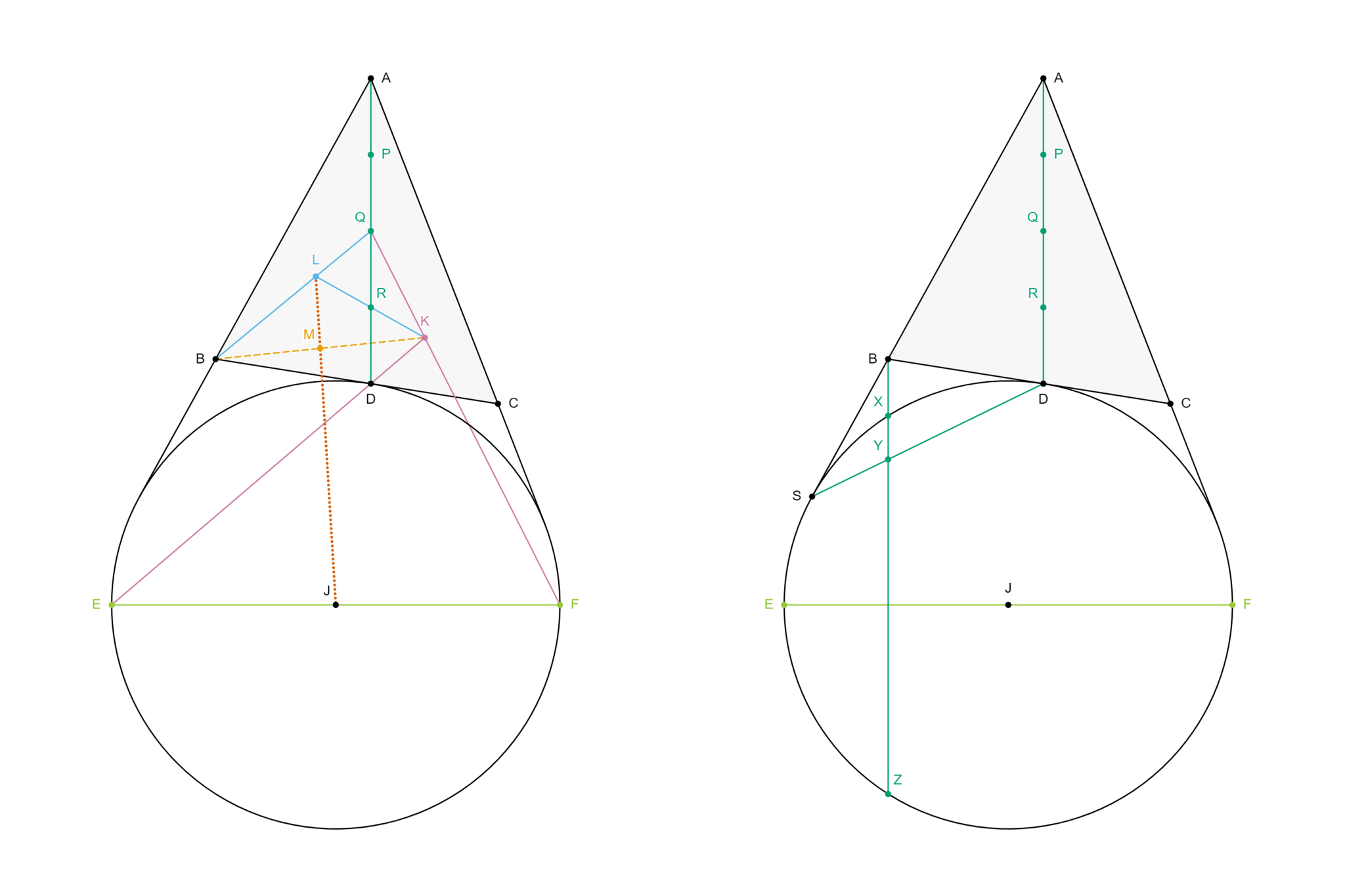カラーバリアフリーを意識して色彩を選んだ割には意外と見づらい

　登場する点の個数が多いため、点

K, L, M

は一旦無視の方向で検討する。代わりに、

A B

と

ω

の接点を

S

とし、

D

と

S

を結ぶ。

B

から引いた

A D

の平行線に対して、これと

ω

の交点を点

B

に近い順で

X, Z

とし、また

D S

との交点を

Y

とする。
　ここまでを図に反映すると、図1右側のようになる。

　

A S = s, A D = d

として、

B X : B Z

を計算しよう。(

A S = A B + B D > A D

より

s > d

であることに注意せよ。)
　

A D ∥ B Z

より

B S : B Y = s : d

、方べきの定理より

B S^{2} = B X \times B Z

であるから

B Y = \frac{d}{s} B S = \frac{d}{s} \sqrt{B X \times B Z} \dots (1)

B D, B S

は

ω

の接線であるため、補題1より

\begin{aligned} B X : X Y & = B Z : Z Y \\ B X \times (B Z - B Y) & = (B Y - B X) \times B Z \\ B Y & = \frac{2 B X \times B Z}{B X + B Z} \dots (2) \end{aligned}

r = \sqrt{s^{2} - d^{2}} > 0

として

(1), (2)

を比較すると

\begin{aligned} \frac{d}{s} \sqrt{B X \times B Z} & = \frac{2 B X \times B Z}{B X + B Z} \\ \frac{d^{2}}{s^{2}} & = \frac{4 B X \times B Z}{(B X + B Z)^{2}} \\ d^{2} B X^{2} - 2 (2 s^{2} - d^{2}) B X \times B Z + d^{2} B Z^{2} & = 0 \\ ((s - r) B X - (s + r) B Z) ((s + r) B X - (s - r) B Z) & = 0 \\ \frac{B X}{B Z} & = \frac{s + r}{s - r}, \frac{s - r}{s + r} \end{aligned}

が判り、

B X < B Z

から

B X : B Z = (s - r) : (s + r)

と導かれる。

\dots (3)

　2点

B, X

の直線

E F

からの距離の比について考える。これは

B Z

と

E F

の交点を

W

としたとき、

B W : X W

を考えることと同義である。
　先の議論で

B X : B Z = (s - r) : (s + r)

を得たため、

W

が線分

X Z

の中点であることに注意すると

B W : X W = \frac{B X + B Z}{2} : \frac{B Z - B X}{2} = s : r

と求められる。即ち、2点

B, X

の

E F

からの距離の比も

s : r

である。
　この事実は、「 $ω$ を $B Z$ 方向に $\frac{s}{r}$ 倍に拡大して得られる楕円 $e_{1}$ 」の周上に点 $B$ が存在することを示している。さらに、全く同様の手法で、点

C

も

e_{1}

の周上に存在することが証明できる。
　ここまでの議論を図に反映すると、図2左側のようになる。

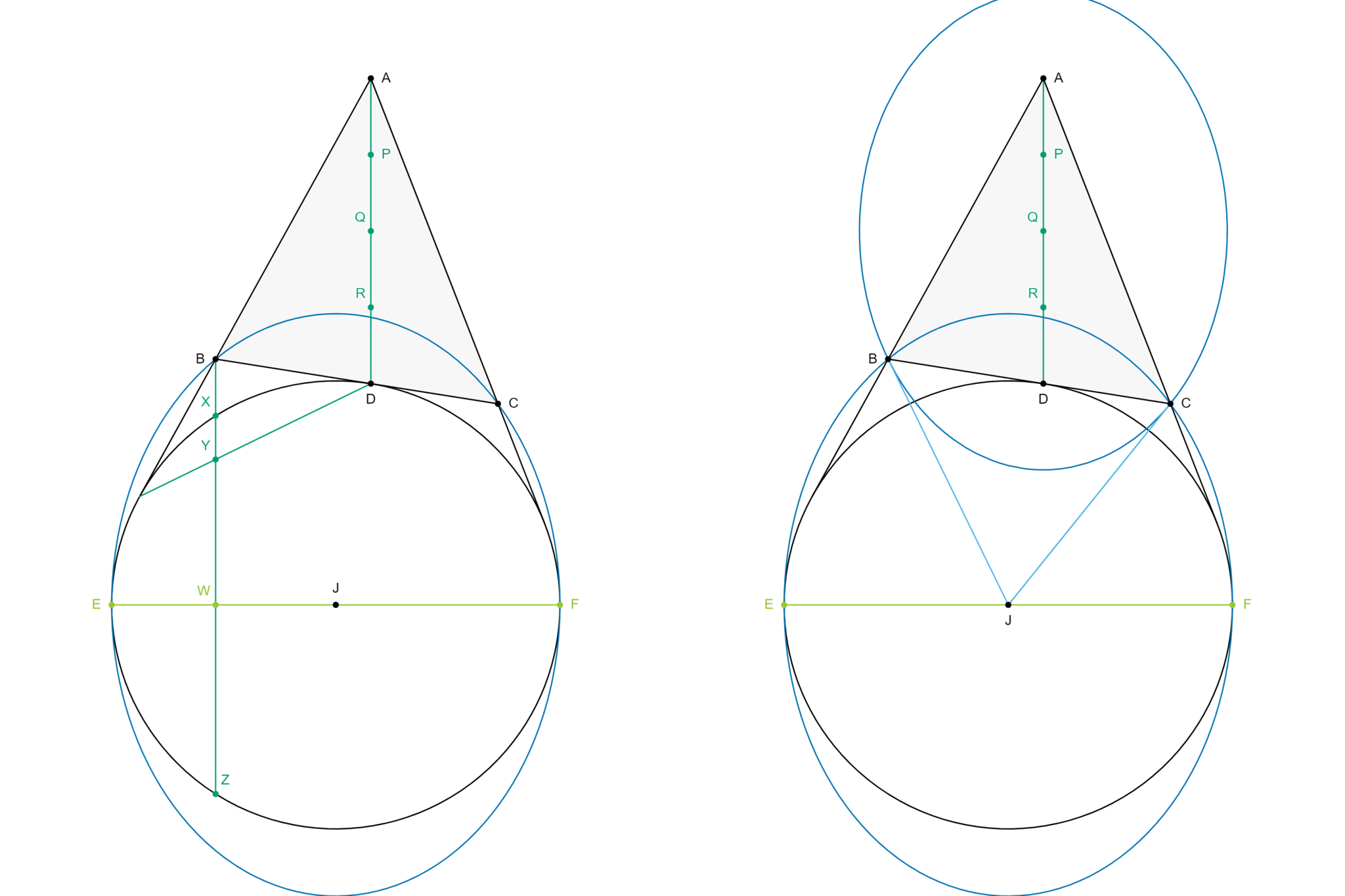作図段階で楕円のサイズを想定していなかったことが分かる貴重な画像

　これ以降、5点

S, W, X, Y, Z

は一切登場しない。

　2点

A, D

を焦点とし、点

B

を通る楕円

e_{2}

を描く。このとき、傍接円の性質から

A B + B D = A C + C D

が判るので、点

C

も

e_{2}

の周上に存在する(楕円は2焦点からの距離の和が一定となる点の軌跡である)。
　また、楕円のもつ有名な性質として『ある焦点から放出された光線は、楕円の周で反射してもう一方の焦点に到達する』(証明は高校数学の美しい物語 - 楕円の反射定理とその証明を参照されたい)というものがある。この性質から、点

B

における

e_{2}

の接線は「

∠ A B D

の外角の二等分線」と一致する、と言える。敢えて記すまでもないが、それは直線

B J

のことである。よって、 $B J$ は点 $B$ で楕円 $e_{2}$ に接する。同様に、

C J

は点

C

で

e_{2}

に接する。
　以上を図に反映すると、図2右側のようになる。

　さて、図2右側に注目していただきたい。何となくではあるが、

e_{1}

と

e_{2}

の形がよく似ているように見えないだろうか。実際、この直感は正しく、 $e_{1}$ と $e_{2}$ は相似である。拡大縮小と平行移動で重なるのだ。今からこれを証明する。と言っても、2つの楕円の長径が明らかに平行なので、長径と短径の比、要するに楕円の縦横比が一致することだけを確認すればよい。
　

e_{1}

が円

ω

を

B Z

方向に

\frac{s}{r}

倍に拡大して得られる楕円であったことを思い出すと、

e_{1}

の縦横比は

s : r

であることが判る。
　

e_{2}

の長径は

A B + B D

の半分、即ち

\frac{s}{2}

である。また、

e_{2}

の焦点間距離は

\frac{d}{2}

であるため、三平方の定理を用いて

e_{2}

の短径を求めると

\frac{\sqrt{s^{2} - d^{2}}}{2} = \frac{r}{2}

となる。したがって、

e_{2}

の縦横比も

s : r

である。
　ゆえに、

e_{1}

と

e_{2}

の縦横比は

s : r

であり、この2つの楕円の相似を確認できた。

　いま、図には2つの楕円と1つの円が描かれている。加えて、2つの楕円は相似であった。
　ここで、図全体を $B Z$ 方向に $\frac{r}{s}$ 倍に縮小してみよう。すると、縦横比が

s : r

であった2つの楕円

e_{1}, e_{2}

は円になる。元々円であった

ω

は残念ながら楕円になってしまうが、扱える円の数が増えただけでも方針が立ちやすくなるはずであるかもしれないという噂をどこかで耳にしたことがあったりなかったりすると考えられる。
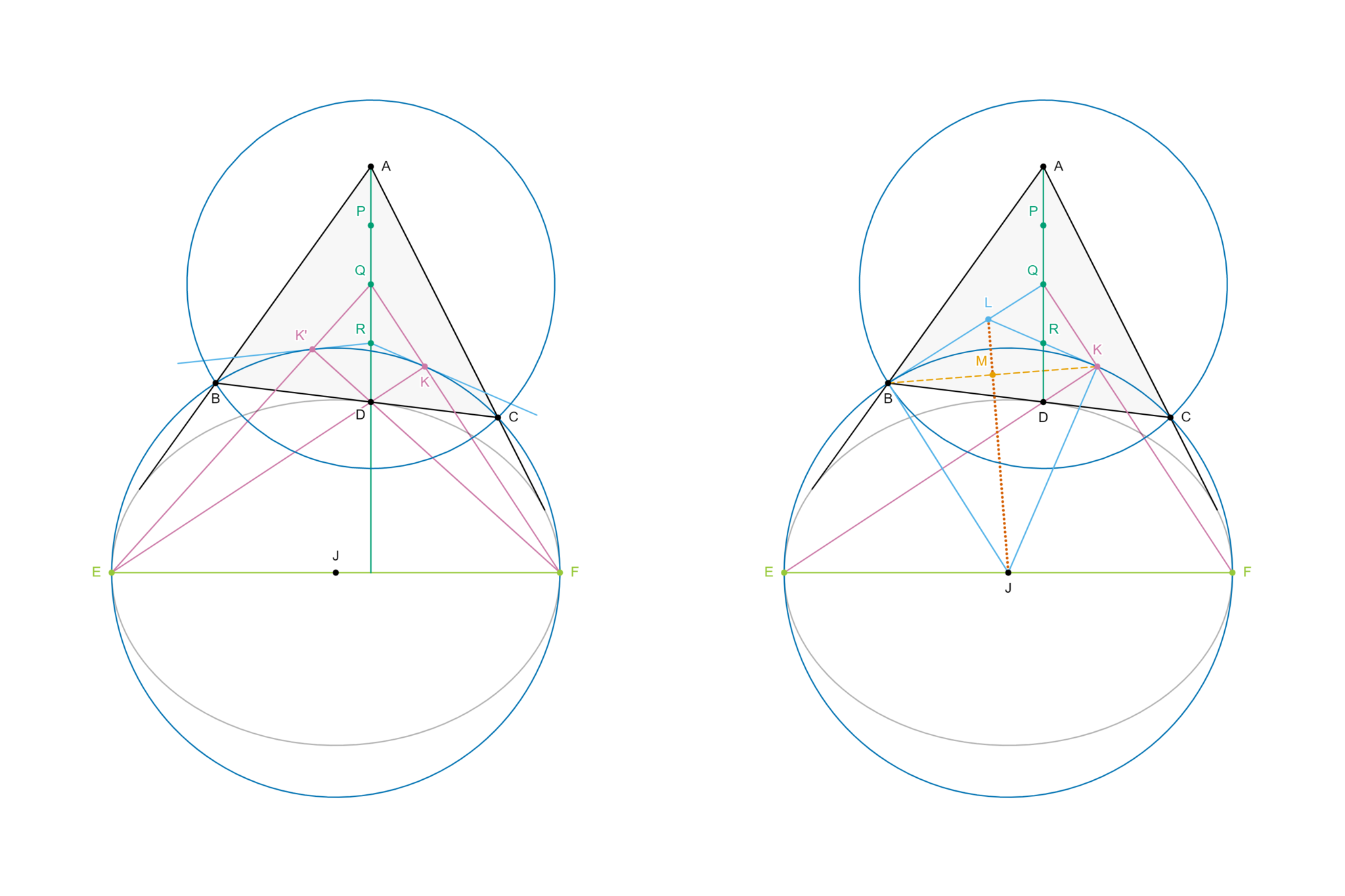
　こうして縮小した図が図3左側である。以下、この縮小した図で考えていこう。(楕円と化してしまった

ω

にもう用は無いため、少し存在感を薄くしてもらった。)

もはや点Jは!FORMULA[138][1896340866][0]の傍心と呼べなくなってしまった…… もはや点Jは $△ A B C$ の傍心と呼べなくなってしまった……

　図を縮小しても接するか否かの関係は変化しないので、

B J, C J

が円

e_{2}

(図の縮小によって円になったことを強調しておく)の接線となっていることも不変である。点

Q

は円

e_{2}

の中心であるから、

∠ Q B J = ∠ Q C J = 90^{\circ}

を得る(これは図3左側における角度である)。よって、点

J

は円

e_{1}

の中心であることを踏まえると、 $B Q, C Q$ は $e_{1}$ に接していると判明する。その接点は当然

B, C

である。
　こんなことを示して何になるのか、と訝る読者も居ることだろう。しかし安心してほしい、この性質もしっかり使う。すぐ後の議論と、証明の終盤で。「まだ終盤に入らないのか」という意見は聞かなかったことにする。

　

A D

と

E F

の交点を

V

とする。

B Q, C Q

は

e_{1}

の接線であったため、補題2から

B V^{2} = C V^{2} = D V \times Q V

が成立する。
　方べきの定理を用いた簡単な計算により

D V \times Q V = E V \times F V

が従うので、

∠ E Q F + ∠ E D F = 180^{\circ}

と言える。直線

Q D

が

E F

に対する垂線であったことに鑑みると、点 $D$ は $△ Q E F$ の垂心と導かれる。よって、直線

D E

は頂点

E

から辺

F Q

に下ろした垂線であり、その足となる点 $K$ は明らかに円 $e_{1}$ 上に存在する。同様に、

D F

と

E Q

の交点

K^{'}

もまた

e_{1}

上に存在する。
　ここまでの議論を図に反映すると、図3右側のようになる。やっと点

K

が登場した。

　

△ D K Q

は

∠ D K Q = 90^{\circ}

の直角三角形であるから、線分

D Q

の中点

R

について

∠ D K R = ∠ K D R

が成り立っている。また、

∠ D K F = ∠ D V F = 90^{\circ}

より四角形

D K F V

は円に内接するので、

∠ K D R = ∠ K F V

も確かめられる。
　以上より

∠ D K R = ∠ K F V = ∠ E F K

となり、接弦定理の逆から $K R$ は点 $K$ で $e_{1}$ に接する。同様に、

K^{'} R

は点

K^{'}

で

e_{1}

に接する。
　このことを図に反映すると、図4左側のようになる。

「爪のピンク色の部分の先端付近に存在する少し白っぽい線」の正式名称はOnychodermal Bandらしい

　歓喜せよ、ついに終盤である。今までの長々と続けてきた議論の中で、本問の根幹に関わる性質は以下の2つ。
　　・ $B Q$ は点 $B$ で $e_{1}$ に接している
　　・ $K R$ は点 $K$ で $e_{1}$ に接している
　さて、点

L

と点

M

を登場させよう。

L

とはどのような点であったか。そう、

B Q

と

K R

の交点だ。ということは、 $e_{1}$ に引いた2本の接線の交点なのだ。

B L = K L

という関係は明らかであろう。

M

は

B K

の中点だ。これらを図に反映させ、不要な点や線を取り除くと、図4右側のようになる。

　これを自明と呼ばずして何と呼ぼうか。念のため、仕上げの過程を記述するが、既に理解できている人は読み飛ばしても構わない。
　

B J = K J, J L = J L

から、三辺相等のため

△ B J L \equiv △ K J L

が判る。それゆえ、 $B$ と $K$ は直線 $J L$ に関して対称な点である。対称な点どうしを結んだ線分の中点は明らかに対称軸に乗るので、点 $M$ は直線 $J L$ 上に存在する。
　図の圧縮によって共線の関係は不変であるため、元の問題図においても点

M

は直線

J L

上に存在すると証明できた。　

◼

あとがき

　個人的には中々の難問に仕上がったと思うのだが、如何だっただろうか。
「図形的考察なんて断固拒否、私は座標で挑む」という方が居たならば、今頃は点

L

の座標(この括弧内に記すつもりだったものの式が長すぎたため頓挫)を求めようとして灰燼に帰しているところだと思われるので、謹んで合掌を送る。
　なお、

(3)

で

B X : B Z

を求められることは匿自身が提示した性質だが、その手順は立見鶏( Twitter )氏によって発見されたものである。彼の貢献が無ければ、このステップにおいて煩雑な計算を要したであろう。

　本問の解説で用いた種々の手法は、いずれも先行研究を見つけられなかったものである。例えば、2点

B, C

が楕円

e_{1}, e_{2}

上に存在し、それら2つの楕円が相似であること、それから

B Q, C Q, K R, K^{'} R

が

e_{1}

の、

B J, C J

が

e_{2}

の接線になること。これらは非常に有用な性質であり、これらを利用して様々な問題を作ることも容易い。
　正直なところ、私は私自身がこれらの性質の第一発見者であるとは考えていない。なぜならば、性質がシンプルである上に、十分な汎用性も備えているからだ。事実、本問のように複雑な構図を煩雑な計算なしで示すことができた。
　読者の中で、もし先行研究をご存知の方が居たら、是非コメントでご教示ねがいたい。

　最後に、本問の類題を紹介して記事を締めくくる。傍心が内心に変わっただけだが、はたしてどのように解けるだろうか。
　以下の類題を証明できた方も、その報告(もしくは解答)をコメントまたは Twitter のDMでお待ちしている。

△ A B C

において、内心を

I

、内接円を

ω

とし、

ω

と

B C

の接点を

D

とする。
　線分

A D

の四等分点を点

A

に近い順で

P, Q, R

と、

A D

と垂直な

ω

の直径の両端を直線

A B

に近い順で

E, F

と、それぞれ名付ける。
　

D E

と

F Q

の交点を

K

、

B Q

と

K R

の交点を

L

としたとき、直線

I L

上に線分

B K

の中点

M

が存在することを示せ。

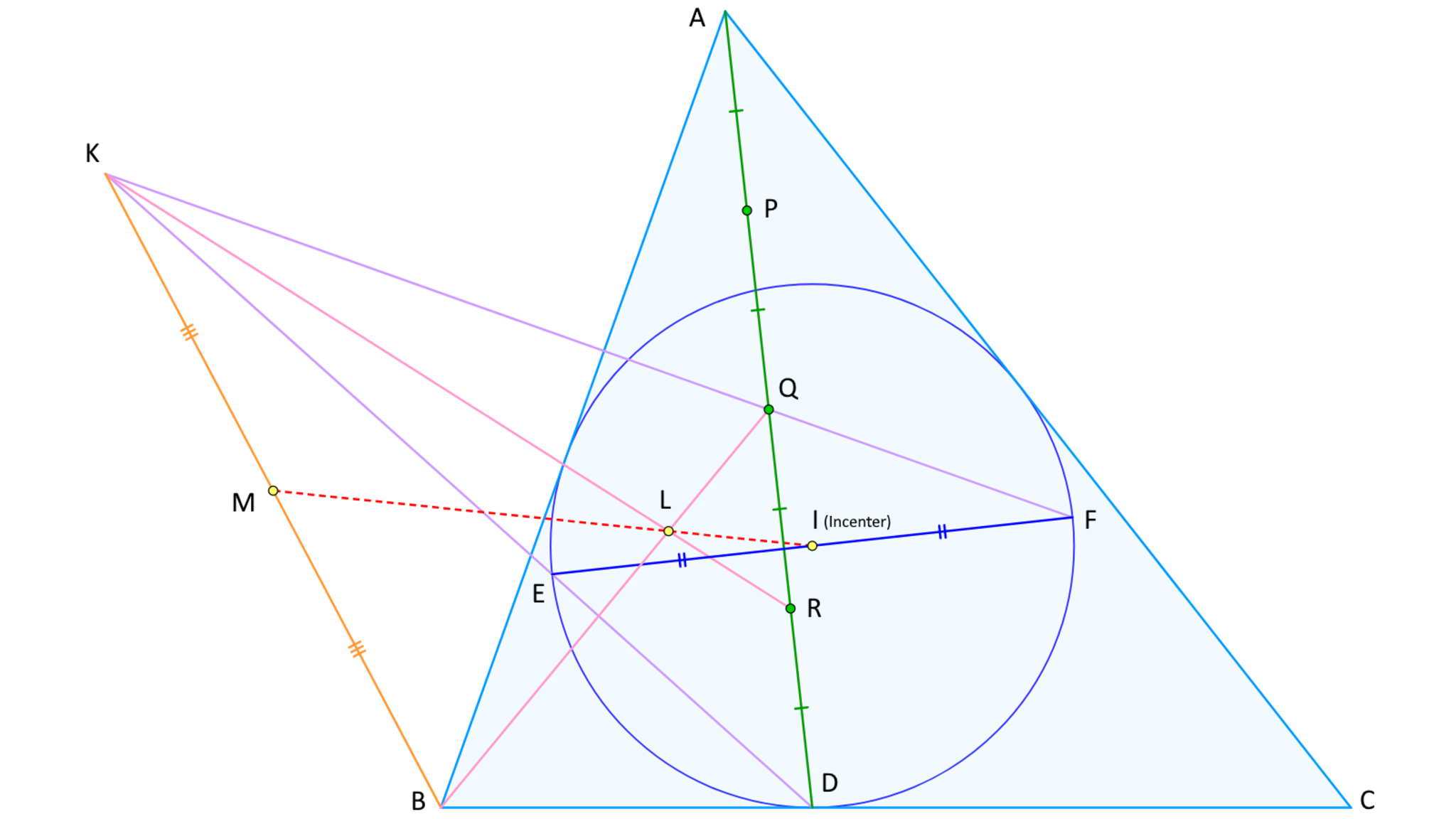そこ、「類題のほうが綺麗じゃん」とか言わない

参考文献

[1]

高校数学の美しい物語 - 調和点列の様々な定義と具体例, 閲覧日 2021年9月25日, https://manabitimes.jp/math/867

[2]

高校数学の美しい物語 - 楕円の反射定理とその証明, 閲覧日 2021年9月25日, https://manabitimes.jp/math/1136

投稿日：2021年9月25日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

匿(Tock)

205

30226

主に初等幾何・レムニスケート。時々偏差値・多重根号。「たとえ作曲家が忘れ去られた日であっても、彼の旋律が街並みを縫って美しく流れていますように。」

他の人のコメント

コメントはありません。

読み込み中

匿(Tock)

柔軟に解く図形問題　〜哲学の深淵にピザは宿る〜

問題
解説
あとがき
参考文献

柔軟に解く図形問題 〜哲学の深淵にピザは宿る〜

問題

解説

あとがき

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

柔軟に解く図形問題　〜哲学の深淵にピザは宿る〜