特異点解消の演習
ネットで適当に拾ってきた演習問題を解きます．
$K$を代数閉体，$X = \mathrm{Spec}K[x,y,z,w]/(xy - zw)$とする．
$X$ の特異点を全て求めよ．
ブローアップで$X$の特異点を解消せよ．
$X$がトーリック多様体と同型であることを示せ．
では早速．
1.1
$f = xy - zw$とする．$X$は4次元空間の中の超曲面であるので，特異点は偏微分が全て0になる点である．それぞれ偏微分を求めると，
\begin{align} f_x &= y \\ f_y &= x \\ f_z &= -w \\ f_w &= -z \end{align}
であるので，
$$ y = x = -w = -z = 0 $$
を解くと$(x,y,z,w) = (0,0,0,0)$となる．
$\therefore$ $\mathrm{Sing}\, X= \{(0,0,0,0)\}$
1.2
何を以てブローアップとするかは文脈による気がするので，なんとなくスケッチだけ書くことにします．
今，$\mathbb{A}^4$の中で原点が特異点となっている:
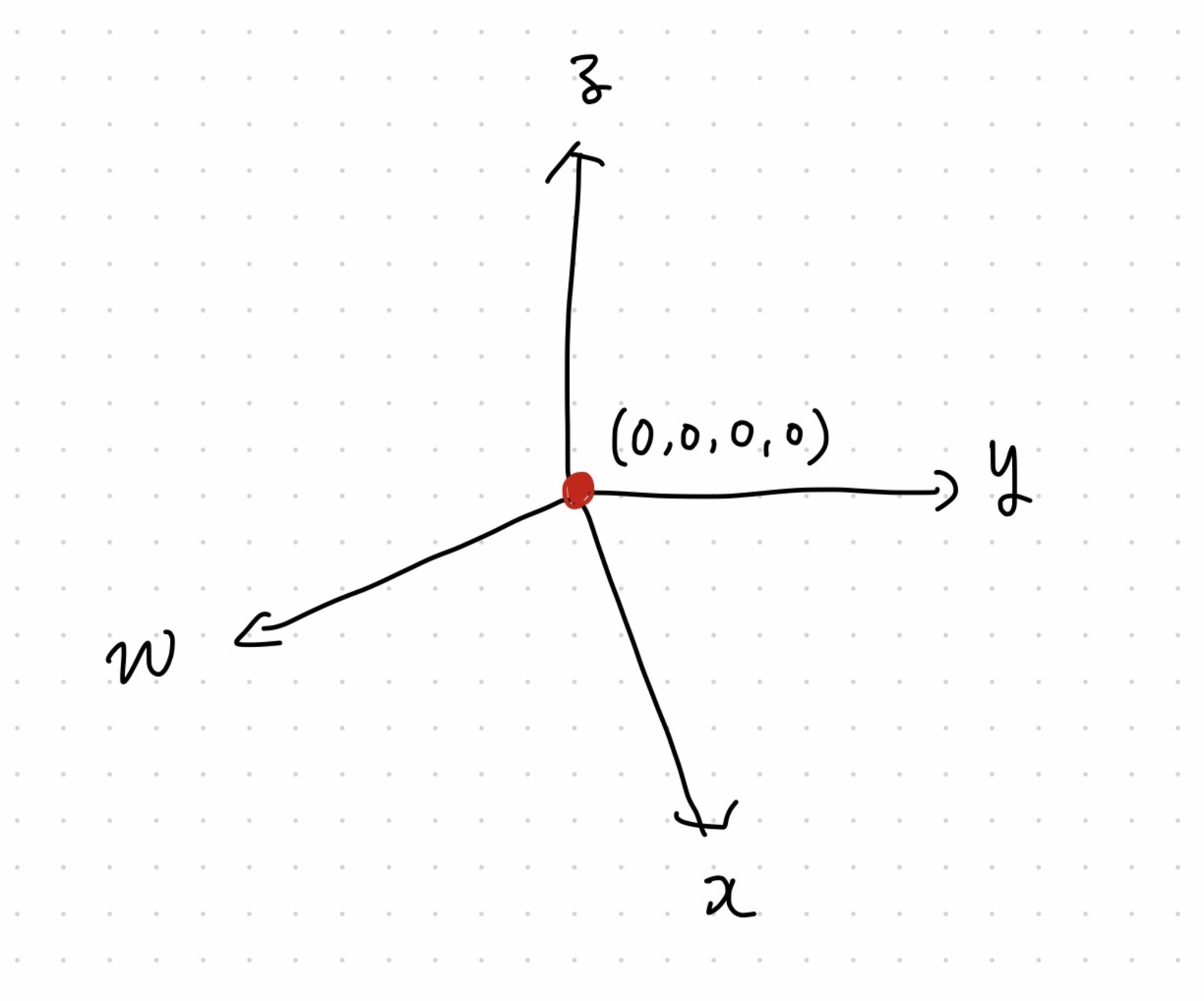4次元空間
これを原点でブローアップしたものを$\mathbb{\tilde{A}}^4$と書くと，以下のようになる:
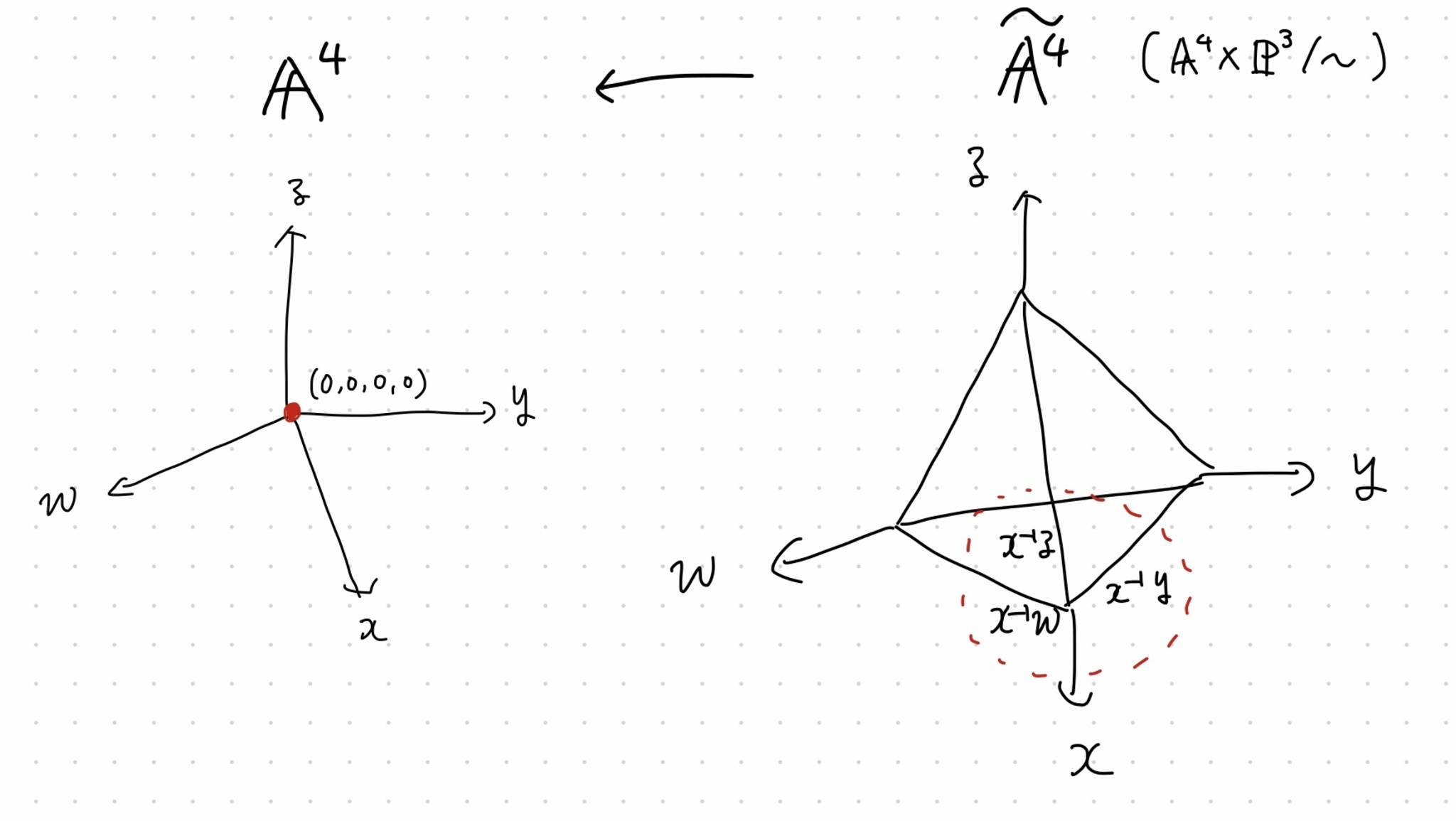原点でブローアップ
$x$が0でない$\mathbb{A}^4$（赤破線部）では軸のラベルが$x, x^{-1}y, x^{-1}z, x^{-1}w$となっているが，それぞれが一つの変数だと考える．
これは局所化したものを便宜的にこう書いているだけです．またこの書き方は流派によって異なり，新しく$y',z',w'$などと変数を置き直すこともあります．
$X$を$\mathbb{\tilde{A}}^4$へ引き戻すと，赤破線部では
$$ xy - zw = x^2(x^{-1}y - (x^{-1}z)(x^{-1}w))) $$
と表せられる．ここで，狭義変換$x^{-1}y - (x^{-1}z)(x^{-1}w) = 0$の多項式を$f^{(x)}$と書くと，
\begin{align}
f^{(x)}_x &= 0 \\
f^{(x)}_{x^{-1}y} &= 1 \\
f^{(x)}_{x^{-1}z} &= - x^{-1}w \\
f^{(x)}_{x^{-1}w} &= - x^{-1}z
\end{align}
となるので，これらを全て0にする点$(x, x^{-1}y, x^{-1}z, x^{-1}w)$は存在しない，よって非特異である．
同様に他の変数でも狭義変換は全て非特異となる．このブローアップの例外集合は$\mathbb{P}^3$に等しい:
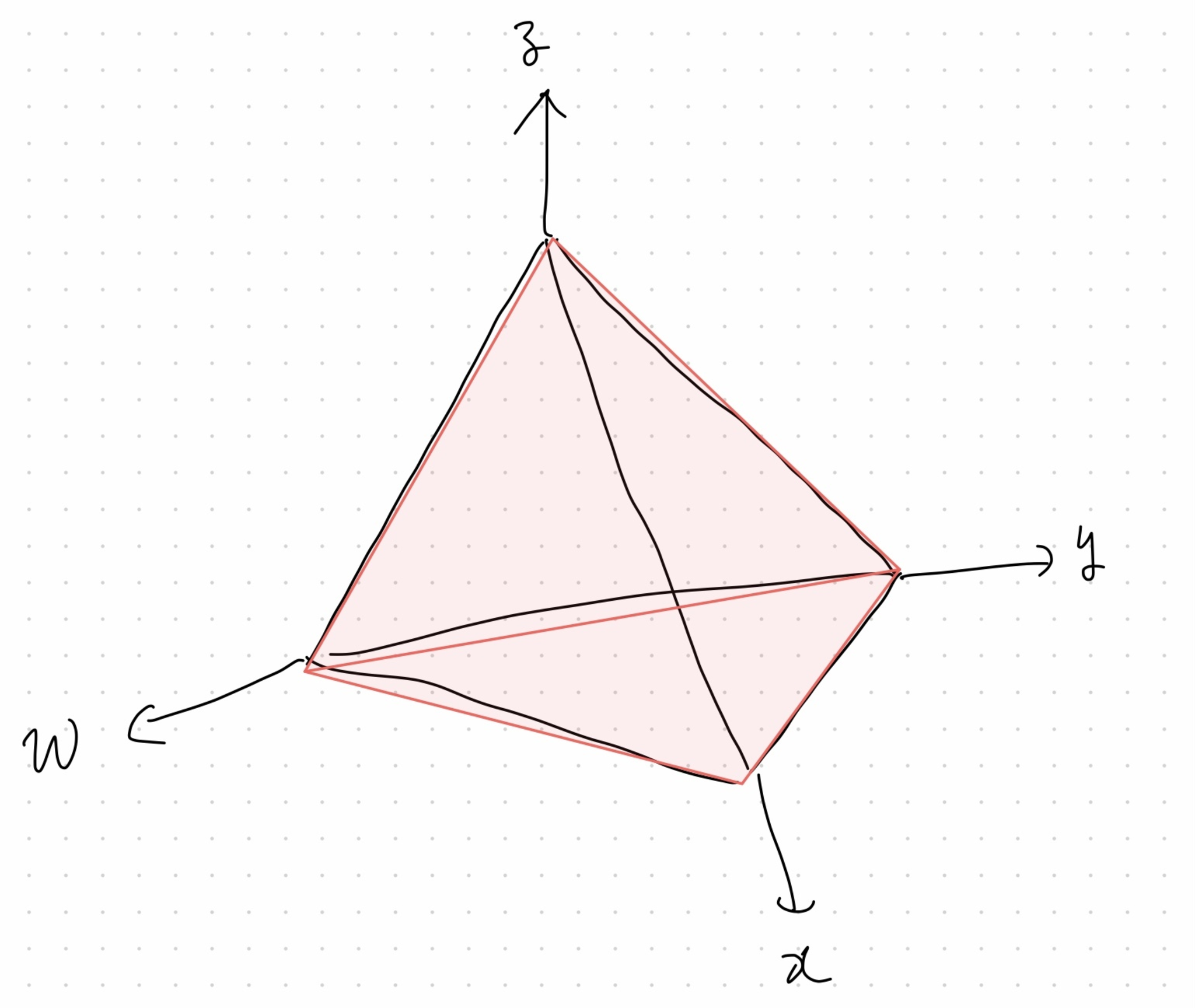例外集合
また，狭義変換は以下のような$\mathbb{P}^3$における射影曲面となる:
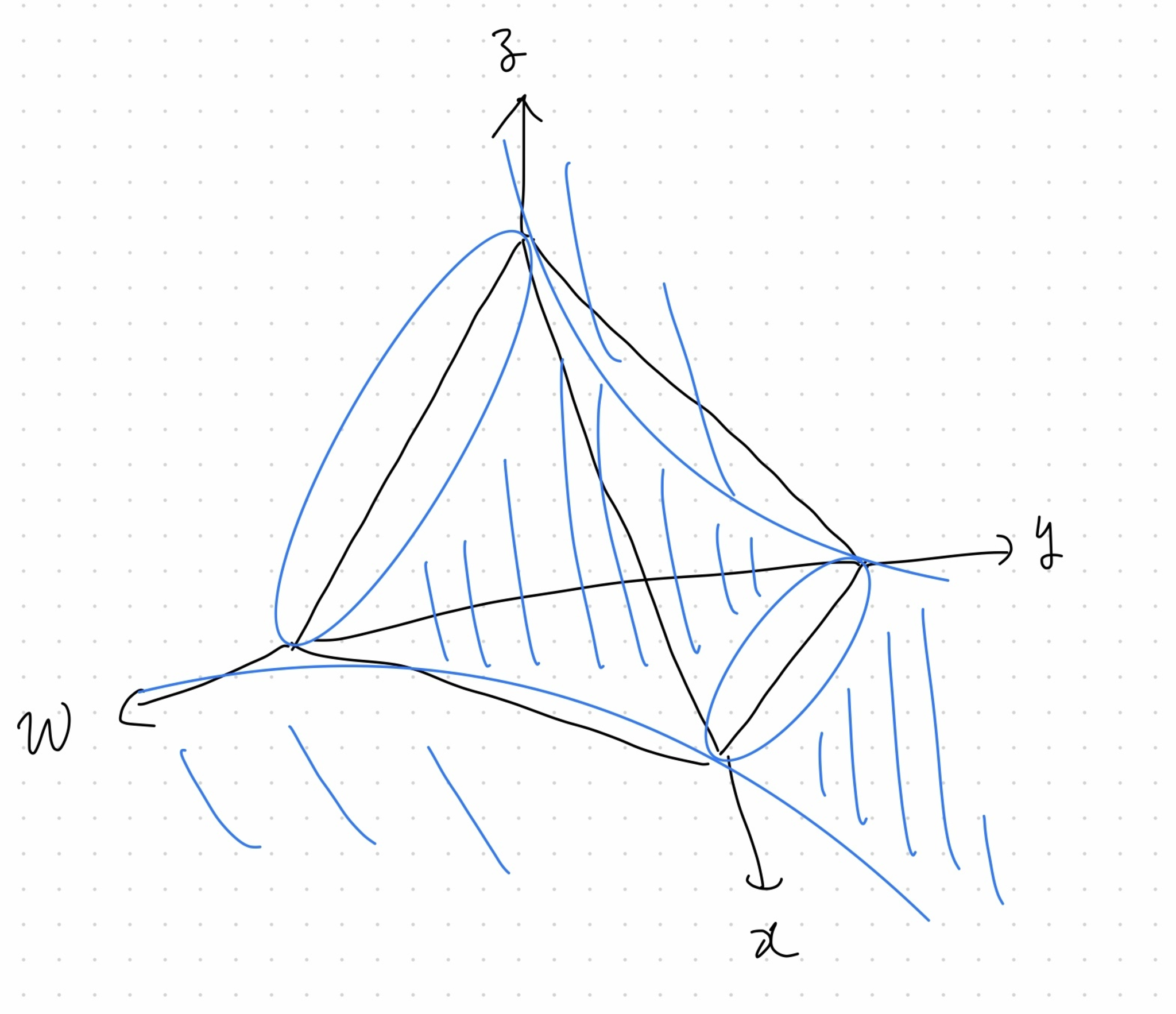狭義変換
全変換をそれぞれ$V_1, V_2, V_3, V_4$とすると，ブローアップは
$$\tilde{X} = V_1 \cup V_2 \cup V_3 \cup V_4 \subset \mathbb{\tilde{A}}^4$$
となる．
1.3
$\phi: K[x,y,z,w] \to K[su,t,u, st] \subset K[s,t,u]$を考える．ここで以下を示す．
$\mathrm{Ker}\, \phi = (xy - zw)$
($\supseteq$) $\phi(xy - zw) = sut - ust = 0$ より成り立つ．
($\subseteq$) $g \in \mathrm{Ker}\, \phi$に対して，
\begin{align}
g &= g(x,y,z,w)\\
&= g_1(y,z, w) + g_2(x, z, w) + g_3(z,w) + (xy - zw)
\end{align}
と剰余しておく．それぞれ$\deg_y g_1 > 0, \deg_x g_2 > 0$であることに注意せよ．
この時，
\begin{align}
\phi(g) &= g_1(t, u, st) + g_2(su, u, st) + g_3(u,st) = 0
\end{align}
となるが，それぞれ$g_1, g_2, g_3$部分に同じ単項式は現れない．実際に，$g_1$と$g_2$で同じ単項式が現れるとすると，それぞれ$t^{a_1}u^{b_1}(st)^{c_1}$および$(su)^{a_2} u^{b_2} (st)^{c_2}$とすると指数部分を比較して
\begin{align} c_1 &= a_2 + c_2\\ a_1 + c_1 &= c_2\\ b_1 &= a_2 + b_2 \end{align}
となるが，これを解くと$a_1 + a_2 = 0$となり，$a_1 > 0, a_2 > 0$に矛盾する．
$g_1$と$g_3$でも同様に比較すると
\begin{align}
c_1 &= b_3\\
a_1 + c_1 &= b_3\\
b_1 &= a_3\\
\end{align}
となるが，これを解くと$a_1 = 0$となり，$a_1 > 0$に矛盾．
$g_2$と$g_3$においても
\begin{align}
a_2 + c_2 &= b_3\\
c_2 &= b_3\\
a_2 + b_2 &= a_3\\
\end{align}
となるが，これを解くと$a_2 = 0$となり，$a_2 > 0$に矛盾．
以上より$K$が無限体であることから$g_1 = g_2 = g_3 = 0$となる．よって$g \in (xy - zw)$となる．$\square$
以上より
$$
K[x,y,z,w]/(xy - zw) \simeq K[su, t, u, st]
$$
が示される．右辺は$s,t,u$の単項式で生成されているので$Y = \mathrm{Spec}\, K[su, t, u, st]$ はトーリック多様体である．
$\therefore$ $X\simeq Y$.
まとめ
ざっとさらったので間違ってるところがあるかもしれません，ご指摘よろしくお願い致します．