結び目のAlexander多項式を計算したい① 結び目補空間のホモロジー群による計算

はじめに
参考文献について
結び目補空間からAlexander不変量の構成
結び目のAlexander加群
諸々の性質とAlexander多項式
本記事で計算したいツイスト結び目のAlexander加群は，幸運なことに単項イデアルによる剰余加群と同型になることが(結果的に)分かります．そこで，次章ではホモロジー群を用いてAlexander多項式の計算を行います．
計算パート
無限巡回被覆空間$\widetilde{X_K}$の具体的な構成
以上により，結び目$K$のSeifert曲面$F$を指定することで$\widetilde{X_K}$の分解を与えることができます．
Seifert曲面と各種ホモロジー群の生成元
本題へ取り組む前の練習問題 : $H_1(X_K) \simeq \Z$
ツイスト結び目のAlexander不変量
応用：Alexander多項式が自明となる結び目たち
サテライト結び目
二重化結び目
あとがき
参考文献

大学数学基礎解説

文献あり

結び目のAlexander多項式を計算したい① 結び目補空間のホモロジー群による計算

結び目理論,Alexander多項式,トポロジー

1516

はじめに

本記事では，Alexander多項式の計算問題としてRolfsen[1]に記載されている次の演習問題をホモロジー群によって計算します．

ツイスト結び目のAlexander多項式

ツイスト結び目 $K = J (2, 2 m)$ のAlexander多項式 $Δ_{K} (t)$ を実際に計算して次であることを確かめよ．
$Δ_{J (2, 2 m)} (t) = m t^{2} + (1 - 2 m) t + m$

ツイスト結び目 $J (2, 2 m)$ とは下の図式から定まる $S^{3}$ 内の結び目です．また箱に書いてある数字は符号を込めた捻り(half-twist)の個数を表しています．

ツイスト結び目!FORMULA[5][2089191634][0] ツイスト結び目 $J (2, 2 m)$

$m = 1$ のとき $J (2, 2)$ は三葉結び目となる．また， $m = - 1$ のとき $J (2, - 2)$ は $8$ の字結び目である．よってそれぞれのAlexander多項式は
$Δ_{J (2, 2)} (t) = - t^{2} + t - 1, Δ_{J (2, - 2)} (t) = t^{2} - 3 t + 1$
となる．

多項式をたくさん計算したい方へ

本末転倒ではありますが，この計算方法は「Alexander多項式を実際に計算する」点においてはあまり効率的でありません．実際，次回紹介する予定の「基本群と行列」を用いた計算方法の方が効率的であると(筆者は)考えています．
ただし，ホモロジー群の具体的な計算練習，結び目の図式を用いたホモロジー代数的計算に触れることができるという点ではとても有意義です．

参考文献について

本記事は全体を通してRolfsen[1]と北野-合田-森藤[2]をベースにまとめています．特に計算パートや二重化結び目については[1]を参照しているので，詳細を確認したい方はそちらを見ていただければと思います．ツイスト結び目を $J (2, 2 m)$ と書いていますが，これは筆者がツイスト結び目と初めて出会った際の記法に準拠しています(Percell[4]-Chpater 7)．

また今月発売された村上[3]にも，今回の内容である無限巡回被覆を用いたAlexander多項式の定義が紹介されています．とても美しいイラストによる解説が載っていますので，必要に応じて参照してもらえればと思います．

結び目補空間からAlexander不変量の構成

今回は無限巡回被覆空間と呼ばれる被覆空間が主な計算対象となります．

位相空間の連続写像 $p : \tilde{X} \to X$ が無限巡回被覆写像であるとは，次を満たすことをいう．

$p$ は被覆写像である．
被覆変換群は $Z$ と同型である．

またこのとき， $\tilde{X}$ を $X$ の無限巡回被覆空間という．

被覆写像 $p$ の被覆変換群 $Aut (p)$ と基本群については，次の短完全列が成り立つことが知られています．
$0 ⟶ π_{1} (\tilde{X}) \overset{p_{*}}{⟶} π_{1} (X) \overset{cok p_{*}}{⟶} Aut (p) ⟶ 0$

結び目のAlexander加群

結び目 $K \subset S^{3}$ の補空間を $X_{K} = S^{3} ∖ K$ とします．

Alexanderの双対定理

結び目補空間 $X_{K}$ の( $Z$ 係数)ホモロジー群は円周 $S^{1}$ のホモロジー群と同型である．

基本群 $π_{1} (X_{K})$ のアーベル化写像(Hurewicz準同型) $α : π_{1} (X) \to H_{1} (X)$ の核 $Ker α$ を考えます．すると $α$ は全射であるため短完全列
$0 ⟶ Ker α \overset{\ker α}{⟶} π_{1} (X) \overset{α}{⟶} H_{1} (X) ⟶ 0$
を得ます．群と被覆空間のガロア対応により，群準同型 $\ker α$ に対応する被覆空間 $p : \tilde{X_{K}} \to X$ が得られます．ここで被覆変換群が $H_{1} (X) ≃ Z$ であるため $\tilde{X_{K}}$ は無限巡回被覆空間となります (後半で $\tilde{X_{K}}$ を具体的に構成するので，難しく考えずに読み飛ばしても大丈夫です)．

次に $\tilde{X_{K}}$ のホモロジー群ついて考えます． $Z$ 係数Laurent多項式環を $Λ = Z [t, t^{- 1}]$ と書くことにします．また被覆変換群 $Aut (p)$ の生成元 $τ$ を $1$ つ取り固定します．

$H_{*} (\tilde{X_{K}})$ は $Λ$ 加群の構造を持つ．

Laurent多項式 $f \in Λ$ と $α \in H_{k} (\tilde{X_{K}})$ に対して積を定めよう． $f (t)$ は次のような係数を持つとする．
$f (t) = c_{- r} t^{- r} + \dots + c_{0} + c_{1} t^{1} + \dots + c_{s} t^{s} (c_{i} \in Z) .$
このとき積 $f \cdot α \in H_{k} (\tilde{X_{K}})$ を
$f \cdot α = c_{- r} τ_{*}^{- r} α + \dots + c_{0} + c_{1} τ_{*}^{1} α + \dots + c_{s} τ_{*}^{s} α \in H_{k} (\tilde{X_{K}})$
によって与えると， $H_{k} (\tilde{X_{K}})$ は $Λ$ 加群の構造を持つことが分かる．ここで $τ : \tilde{X_{K}} \to \tilde{X_{K}}$ は上で固定した被覆変換群の生成元であり， $τ_{*} : H_{k} (\tilde{X_{K}}) \to H_{k} (\tilde{X_{K}})$ は $τ$ から誘導される群同型写像，そして $τ_{*}^{i}$ は $τ_{*}$ の $i$ 回の合成である．

結び目 $K$ から得られる $Λ$ 加群 $H_{*} (\tilde{X_{K}})$ を，結び目 $K$ のAlexander加群という． $H_{*} (\tilde{X_{K}})$ は結び目の不変量である．

諸々の性質とAlexander多項式

先ほど定義したAlexander加群の性質について見ていきましょう．Laurent多項式 $f \in Λ$ で生成されるイデアルを $(f)$ と記すことにします．

$Λ$ 加群として $H_{0} (\tilde{X_{K}}) ≃ Λ / (t - 1)$ である．

$\tilde{X_{K}}$ は弧状連結であるので，群として $H_{0} (\tilde{X_{K}}) ≃ Z$ であることに注意する．生成元 $α \in H_{0} (\tilde{X_{K}})$ と任意の $r \in Z$ に対して $τ_{*}^{k} α = α$ であるから， $f$ による積は $f$ の係数の和となる．よって $f \cdot α = f (1) α$ となり主張を得る．

また2次以上のAlexander加群についても次が成り立ちます(証明は割愛します)．

整数 $k \geq 2$ に対して $H_{k} (\tilde{X_{K}}) = 0$ である．

よってAlexander加群 $H_{*} (\tilde{X_{K}})$ は1次ホモロジー群以外には情報がないことが分かります．

結び目 $K_{1}$ と $K_{2}$ の連結和を $K = K_{1} # K_{2}$ とする．このとき $K$ のAlexander加群は $K_{1}$ と $K_{2}$ のAlexander加群の直和と同型である．
$H_{1} (\tilde{X_{K}}) ≃ H_{1} (\tilde{X_{K_{1}}}) \oplus H_{1} (\tilde{X_{K_{2}}})$

結び目の連結和は， $2$ つの結び目を隔てる球面 $S^{2} \subset S^{3}$ を用いて定義されていた．この分離球面によって $S^{3}$ は $2$ つの $3$ 次元球体に分離されるが，この分離した球体に関するMayer-Vietoris完全系列を計算することで主張を得る(詳細は[1]の7E-1を参照されたい)．

$H_{1} (\tilde{X_{K}})$ を用いることにより，次の場合には直ちにAlexander多項式が定義できます．

$H_{1} (\tilde{X_{K}}) ≃ Λ / (f_{1}) \oplus \dots \oplus Λ / (f_{m})$ ( $f_{i} \in Λ = Z [t^{\pm 1}], i = 1, 2, \dots, m$ )となるとき，Laurent多項式の積 $Δ_{K} (t) = f_{1} f_{2} \dots f_{m}$ を $K$ のAlexander多項式と呼ぶ．Alexander多項式は $\pm t^{i}$ 倍の差を除いて結び目不変量である．

現在勉強中につき不明確な箇所

$Λ = Z [t^{\pm 1}]$ は単項イデアル整域ではないため， $H_{1} (\tilde{X_{K}})$ が上記の形に書けるとは限らない？
上の定義では全ての結び目に対してAlexander多項式が定義ができない？しかし次回に紹介する予定のAlexander行列を用いると，全ての結び目に対してAlexander多項式 $Δ_{K} (t)$ が定義できる．
ホモロジー群によるAlexander多項式の解釈は，Reidemeisterトーションと呼ばれる概念を用いることで可能らしい？

(詳しい方がいましたら，コメントしていただけると助かります．)
追記：下部のコメント欄にて，ルシアンさんより解説コメントをいただきました．感謝いたします！

本記事で計算したいツイスト結び目のAlexander加群は，幸運なことに単項イデアルによる剰余加群と同型になることが(結果的に)分かります．そこで，次章ではホモロジー群を用いてAlexander多項式の計算を行います．

補足: Alexanderの双対定理

最初に登場した「Alexanderの双対定理」は結び目の補空間を調べる上でとても有用な定理です．

Alexanderの双対定理

$X \subset S^{n}$ をコンパクトかつ局所可縮な部分空間とする．また， ${\tilde{H}}_{*}$ を簡約ホモロジー群とする．
このとき次が成り立つ．
${\tilde{H}}_{k} (S^{n} ∖ X) ≃ {\tilde{H}}^{n - k - 1} (X), (k \in Z) .$

計算パート

無限巡回被覆空間 $\tilde{X_{K}}$ のホモロジー群を計算していきたいと思います．ホモロジー群の計算方法としては最も一般的であるMayer-Vietoris完全系列を用います．そのためには，まず $\tilde{X_{K}}$ を $2$ つのパーツに分解しましょう．

無限巡回被覆空間 $\tilde{X_{K}}$ の具体的な構成

次に定める $Y$ と $N$ によって $X_{K}$ を分解し，そして $\tilde{X_{K}}$ を構成します．ここで $M$ の内部を $\overset{˚}{M}$ で表します．

$K$ は $S^{3}$ 内の結び目．
$X_{K} := S^{3} ∖ K$ は結び目 $K$ の補空間．
$F$ は $K$ のSeifert曲面( $K$ を境界に持つ $S^{3}$ 内の向き付けられたコンパクト曲面)．
$N \approx \overset{˚}{F} \times (- 1, 1)$ は $X_{K}$ における $F$ の正則開近傍．
$Y := S^{3} ∖ F, Y \cap N =: N^{-} \cup N^{+} \approx \overset{˚}{F} \times (- 1, 0) \cup \overset{˚}{F} \times (0, 1)$ ．

構成から $Y \cup N = X$ となることに注意します．
いま，各整数 $i$ について $Y$ , $N$ のコピーを $Y_{i}$ , $N_{i}$ ， $Y_{i} \cap N_{i} =: N_{i}^{-} \cup N_{i}^{+}$ とおき，次のペア $(1)$ $Y_{i}$ と $N_{i}$ $(2)$ $Y_{i + 1}$ と $N_{i}$ を次のようにして貼り合わせます．

$Y_{i}$ と $N_{i}$ は，それぞれの $N_{i}^{+}$ を自然に同一視することで貼り合わせる．
$Y_{i + 1}$ と $N_{i}$ は，それぞれの $N_{i + 1}^{-}$ と $N_{i}^{-}$ を自然に同一視することで貼り合わせる．

すると，全ての $i \in Z$ で貼り合わせて得られる空間を $\tilde{X}$ とします．

!FORMULA[146][730828657][0]の貼り合わせのスキーム図 $\tilde{X}$ の貼り合わせのスキーム図

空間 $\tilde{X}$ は結び目補空間 $X_{K}$ の無限巡回被覆空間 $\tilde{X_{K}}$ と一致する．

$X_{i} := Y_{i} \cup N_{i}$ とする．被覆写像 $p : \tilde{X} \to X_{K}$ は各 $X_{i}$ を $X$ へ自然に射影することで与えられる．また $X_{i}$ を $X_{i + 1}$ に平行移動させる写像 $τ : \tilde{X_{K}} \to \tilde{X_{K}}$ は被覆変換群 $Aut (p)$ の元となり，さらに $Aut (p)$ を生成する位数 $0$ の元であることが分かる．

以上により，結び目 $K$ のSeifert曲面 $F$ を指定することで $\tilde{X_{K}}$ の分解を与えることができます．

Seifert曲面と各種ホモロジー群の生成元

$\tilde{X_{K}}$ のホモロジー群をMayer-Vietoris完全系列を用いて計算するために，必要な各種のホモロジー群の表示を与えます．手順としては次の $2$ ステップです．

$X_{K}$ 内の $4$ つの図形について，ホモロジー群を表示する．
$X_{K}$ での議論を $\tilde{X_{K}}$ へ拡張する．

ループとホモロジー群の元

簡単のために，ホモロジー群の元をループ(閉曲線)によって表すことにします．例えば，ループ $α \subset X$ が属するホモロジー群の元 $[α] \in H_{1} (X)$ を単に $α$ と記します．

これ以降はツイスト結び目に対する準備を進めていきますが，同様の方法によってその他の結び目についても計算が可能となります．
まず結び目 $K = J (2, 2 m)$ のSeifert曲面 $F$ を以下で定めます．

!FORMULA[174][2089191634][0]のSeifert曲面 $J (2, 2 m)$ のSeifert曲面

つまり， $K$ のSeifert曲面 $F$ (左)は $2 m$ 回捻りを行ったアニュラス(中央)と $2$ 回捻りのバンド(右)をアニュラスの上部に張り合わせることによって得られます． $F$ はトーラスから(開)円板を $1$ 枚くり貫いてできる曲面と同相です．またホモロジー群 $H_{1} (F)$ は次で表されるループ $a$ と $b$ によって生成されます．そこで $Z$ 加群としての表示 $H_{1} (F) = ⟨ a, b ⟩$ を固定します．

!FORMULA[186][558700303][0]の生成元 $H_{1} (F)$ の生成元

$Y$ のホモロジー群を考えましょう．ホモロジー群 $H_{1} (Y)$ は次のループ $α$ と $β$ から生成させることが分かります．(生成元が $2$ つであることは，Alexanderの双対定理によって分かります．)

!FORMULA[192][558718562][0]のホモロジー群の生成元 $H_{1} (Y)$ のホモロジー群の生成元

次に $N$ のホモロジー群を考えましょう． $N$ と $F$ (さらに $N^{+}$ と $N^{-}$ )はホモトピー同値なので，それぞれのホモロジー群は $a$ と $b$ から誘導されるループによって生成されます．特に $H_{1} (N^{+})$ と $H_{1} (N^{-})$ へ誘導される生成元を $a^{+}$ , $b^{+}$ と $a^{-}$ , $b^{-}$ によって記します．

最後に， $Y$ と $N$ の共通部分が連結となるようにひと手間を加えましょう．次のような $X_{K}$ 内のループ $γ$ を考えます． $N$ は $F$ の正則近傍だったので， $γ ⊄ N$ となります( $γ$ は結び目のメリディアンとも呼ばれます)．

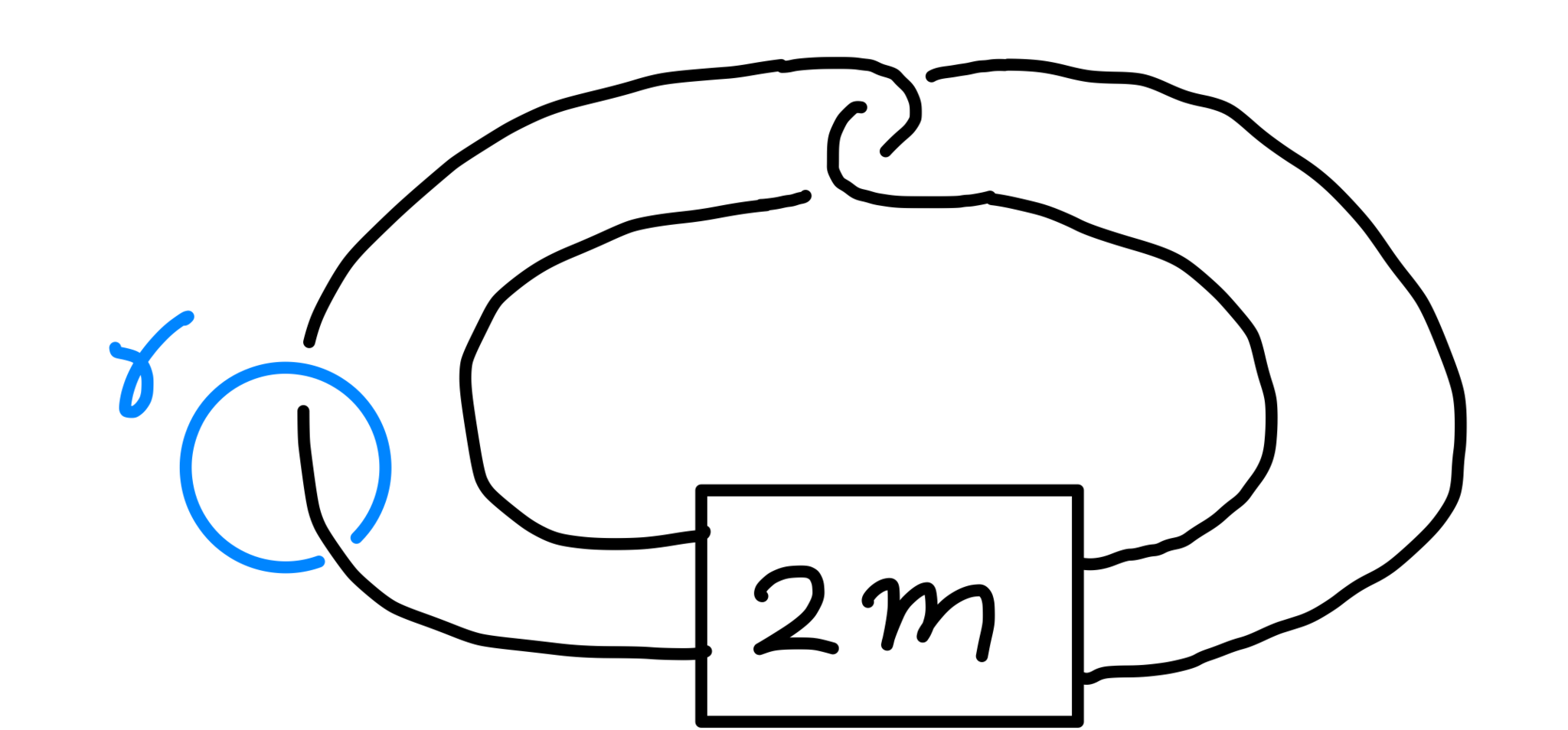結び目のメリディアン

すると $(Y \cup γ) \cap (N \cup γ) = N^{+} \cup N^{-} \cup γ$ は連結な位相空間(CW複体)となり， $(Y \cup γ) \cup (N \cup γ) = X_{K}$ を満たします．そこで， $Y \cup γ$ と $N \cup γ$ を改めて $Y, N$ と書くことにします．

また $Y$ と $N$ の1次ホモロジー群にはそれぞれ $γ$ が生成元に加わります． $H_{1} (Y)$ と $H_{1} (N)$ の生成元 $γ$ を区別するために， $H_{1} (Y)$ の生成元は $γ_{Y}$ ， $H_{1} (N)$ の生成元は $γ_{N}$ と書くことにしましょう．

以上をまとめて次の補題となります．

ツイスト結び目の補空間 $X_{K}$ 内の図形について，次のような $Z$ 加群としての表示を持つ．
$H_{1} (Y) = ⟨ α, β, γ_{Y} ⟩, H_{1} (N) = ⟨ a, b, γ_{N} ⟩, H_{1} (N^{+}) = ⟨ a^{+}, b^{+} ⟩, H_{1} (N^{-}) = ⟨ a^{-}, b^{-} ⟩ .$

本題へ取り組む前の練習問題 : $H_{1} (X_{K}) ≃ Z$

本題へ取り組む前の練習問題として，結び目補空間のホモロジー群 $H_{1} (X_{K})$ を計算してみましょう．
$X_{K} = Y \cup N$ だったので，次のMayer-Vietoris完全系列を得ます．
$\dots \overset{δ_{k + 1}}{⟶} H_{k} (Y \cap N) \overset{j_{k}}{⟶} H_{k} (Y) \oplus H_{k} (N) \overset{q_{k}}{⟶} H_{k} (X_{K}) \overset{δ_{k}}{⟶} \dots (k \in Z) .$

ここで $Y \cap N$ は連結なので，準同型 $j_{0}$ は単射となります．よって同型
$H_{1} (X_{K}) ≃ H_{1} (Y) \oplus H_{1} (N) / Im j_{1}$
が得られます．また上の構成から $H_{1} (Y) \oplus H_{1} (N)$ は $α, β, γ_{Y}, a, b, γ_{N}$ によって生成される $Z$ 加群となります．

それでは $Im j_{1}$ を求めましょう． $Y \cap N = N^{+} \cup N^{-} \cup γ$ でしたので， $H_{1} (Y \cap N)$ は $a^{+}, b^{+}, a^{-}, b^{-}, γ$ によって生成される $Z$ 加群です．よって各生成元の $j_{1}$ の像を計算すればよいことになります．

Im j_{1}

の生成元

ツイスト結び目 $K = J (2, 2 m)$ の補空間 $X_{K}$ について，部分加群 $Im j_{1}$ は次の元たちによって生成される．
$Im j_{1} = ⟨ m α + β + a, m α + a, β + b, α + β + b, γ_{Y} + γ_{N} ⟩ .$

この命題の証明が本記事における最重要ポイントです．なぜならツイスト結び目の絡まりの複雑さが $Im j_{1}$ に現れており，この複雑度を多項式によって表したものがAlexander多項式となるからです．

$Im j_{1}$ を計算するために， $H_{1} (Y)$ と $H_{1} (N)$ への像を別々に確かめよう．ここで $j_{1}$ は自然な埋め込みから誘導される群準同型であった．

まず最初に $H_{1} (Y)$ における像を考える．そのためには $Y$ 内のループ $a^{+}, b^{+}, a^{-}, b^{-}$ を生成元 $α, β, γ_{Y}$ によって表せばよい．
図式にループ $a^{+}, b^{+}, a^{-}, b^{-}$ を描くことを考えよう．このとき次のようにループ $a, b$ を「ずらす」ことで得られていた．ここで $a^{+}$ は紙面の表側に， $a^{-}$ は紙面の裏側にずらすことで得られるとし， $b^{+}$ と $b^{-}$ は灰色の面で同様にずらすことを赤い面に拡張することで記述する(Seifert曲面 $F$ は向き付け可能であったため，この操作はwell-efinedである)

ループの平行移動

次のイラストは $m = 2$ における $a^{+}, b^{+}, a^{-}, b^{-}$ である．

!FORMULA[271][-1654901838][0]のイラスト $a^{+}, b^{+}, a^{-}, b^{-}$ のイラスト

イソトピー変形をすることで， $a^{+}$ はホモロジー群 $H_{1} (Y)$ 内では $2$ つの $α$ と $1$ つの $β$ によって生成されることが分かる．

ループ!FORMULA[278][36228186][0]のイソトピー変形ループ $a^{+}$ のイソトピー変形

他のループについても同様に変形することによって， $j_{1}$ による $H_{1} (Y)$ への像は次のようになる．

$\begin{array}{r} {\begin{cases} j_{1} (a^{+}) = 2 α + β, \\ j_{1} (b^{+}) = β, \end{cases} {\begin{cases} j_{1} (a^{-}) = 2 α, \\ j_{1} (b^{-}) = α + β, \end{cases} j_{1} (γ) = γ_{Y} . \end{array}$

$m$ が一般の整数の場合においても同様の計算が可能であり，次のようになる．

$\begin{array}{r} {\begin{cases} j_{1} (a^{+}) = m α + β, \\ j_{1} (b^{+}) = β, \end{cases} {\begin{cases} j_{1} (a^{-}) = m α, \\ j_{1} (b^{-}) = α + β, \end{cases} j_{1} (γ) = γ_{Y} . \end{array}$

一方で， $j_{1}$ による $H_{1} (N)$ への像はとてもシンプルなものになっている．
$j_{1} (a^{\pm}) = a, j_{1} (b^{\pm}) = b, j_{1} (γ) = γ_{N} .$
そこで直和を単に足し算の記号で書くことにすれば， $Im j_{1}$ は次で生成される $H_{1} (Y) \oplus H_{1} (N)$ の部分加群となり証明が完了する．
$Im j_{1} = ⟨ m α + β + a, m α + a, β + b, α + β + b, γ_{Y} + γ_{N} ⟩ .$

ツイスト結び目 $K = J (2, 2 m)$ の補空間 $X_{K}$ について， $H_{1} (X_{K}) ≃ Z$ である．

剰余加群 $H_{1} (Y) \oplus H_{1} (N) / Im j_{1}$ について考えると，
$a = - m α, b = - β, γ_{Y} = - γ_{N}, a = 0, b = 0$
という $5$ つの関係式となる．よって $H_{1} (X_{K})$ は $γ_{Y}$ によって生成される無限巡回群( $≃ Z$ )と同型である．

ツイスト結び目のAlexander不変量

それではいよいよ $K = J (2, 2 m)$ のALexander加群の計算を行いましょう．つまり $\tilde{X_{K}}$ の1次ホモロジー群を計算しましょう． $\tilde{Y}$ と $\tilde{N}$ を，無限巡回被覆 $p : \tilde{X_{K}} \to X_{K}$ による $Y$ と $N$ の逆像として定めます．

持ち上げた空間の取り扱いについて

$Y_{i}, N_{i}, X_{i}$ について少し煩雑な記号の扱いをします． $Y_{i}, N_{i}, X_{i}$ の定義は $Y$ や $N$ が $γ$ を含んでいない場合に定義しましたが，この後に再登場する彼らも同様に $γ$ を含まない場合の定義を採用します．

$Y_{new} = Y_{old} \cup γ, N_{new} = N_{old} \cup γ$ ．
$Y_{i}$ は $Y_{old}$ のコピー， $N_{i}$ は $N_{old}$ のコピー．
$X_{i} = Y_{i} \cup N_{i}$ ．

各位相空間(CW複体) $\tilde{Y}, \tilde{N}, \tilde{Y} \cap \tilde{N}$ は連結である．

ループ $γ \subset X_{K}$ の $p$ による逆像 $\tilde{γ} = p^{- 1} (γ)$ を考える．すると $3$ 章で与えた $\tilde{X_{K}}$ の構成から， $\tilde{γ}$ は $\tilde{X_{K}}$ を縦断する一本の曲線となる(下図のオレンジ色の横線)．つまり被覆写像 $p$ によって $X_{i}$ へ持ち上がる $γ$ の逆像 $γ_{i}$ は， $X_{i + 1}$ への持ち上げ $γ_{i + 1}$ と繋がっている．

!FORMULA[332][971969835][0]たちは繋がっている． $γ_{i}$ たちは繋がっている．

よって $\tilde{Y}, \tilde{N}$ は，各 $Y_{i}, N_{i}$ を縦断する曲線 $\tilde{γ}$ によって串刺しにした空間となり連結となる．同様にして
$\tilde{Y} \cap \tilde{N} = ⋃_{i \in Z} (N_{i}^{+} \cup N_{i}^{-} \cup γ_{i}) = ⋃_{i \in Z} (N_{i}^{+} \cup N_{i}^{-}) \cup \tilde{γ}$
となるので連結性が分かる．

証明から分かるように， $\tilde{γ}$ は $\tilde{Y}$ や $\tilde{N}$ においてホモロジー群の生成元ではありません．また上の注意より $H_{1} (Y_{i})$ と $H_{1} (N_{i})$ は $2$ 元生成の $Z$ 自由加群でした．

よって次の補題を得ます．

$H_{1} (Y_{i}) = ⟨ α_{i}, β_{i} ⟩, H_{1} (N_{i}) = ⟨ a_{i}, b_{i} ⟩ (i \in Z)$ とするとき， $H_{1} (\tilde{Y})$ と $H_{1} (\tilde{N})$ は次のような $Z$ 加群である．
$H_{1} (\tilde{Y}) = ⟨ α_{i}, β_{i} | i \in Z ⟩, H_{1} (\tilde{N}) = ⟨ a_{i}, b_{i} | i \in Z ⟩ .$

消えた生成元

γ

$H_{1} (X_{K}) ≃ Z$ の証明で見たように， $γ$ は $H_{1} (X_{K})$ の生成元となっていました．そのため， $γ$ は $\tilde{X_{K}}$ の被覆変換群 $Aut (p)$ の生成元として立ち振る舞っています．

$2$ 章で行った議論を思い出すと，被覆変換群 $Aut (p) ≃ ⟨ τ ⟩$ の作用によって $H_{1} (\tilde{X_{K}})$ は $Λ$ 加群の構造を持つのでした．同様に被覆変換群は $H_{1} (\tilde{Y})$ と $H_{1} (\tilde{N})$ にも作用し $Λ$ 加群の構造を与えます．

また $H_{1} (\tilde{Y})$ と $H_{1} (\tilde{N})$ の生成元 $α_{i}, β_{i}, a_{i}, b_{i}$ に対して $τ$ は添え字を $k \to k + 1$ へ移す作用となります．そこで $α_{0}$ を単に $α$ と記し，各 $α_{i}$ を $α t^{i}$ と書くことにすれば( $β_{i}, a_{i}, b_{i}$ についても同様)， $H_{1} (\tilde{Y})$ と $H_{1} (\tilde{N})$ は $Λ$ 加群として $α, β$ と $a, b$ で生成されていることになります．

$\tilde{Y}$ と $\tilde{N}$ の $1$ 次ホモロジー群は $Λ$ 加群として次の表示を持つ．
$H_{1} (\tilde{Y}) ≃ ⟨ α, β ⟩_{Λ}, H_{1} (\tilde{N}) ≃ ⟨ a, b ⟩_{Λ} .$

以上の準備をもとに，いよいよ計算を行っていきましょう．

ツイスト結び目のAlexander加群

ツイスト結び目 $K = J (2, 2 m)$ ( $m \in Z$ ) に対して， $H_{1} (\tilde{X_{K}})$ は $Λ$ 加群として次と同型である．
$H_{1} (\tilde{X_{K}}) ≃ Λ / (m t^{2} + (1 - 2 m) t + m) .$

$H_{1} (X_{K})$ のときと同様に，次のMayer-Vietoris完全系列を用いてホモロジー群の計算を行う．
$\dots \overset{\tilde{δ_{i + 1}}}{⟶} H_{k} (\tilde{Y} \cap \tilde{N}) \overset{\tilde{j_{k}}}{⟶} H_{k} (\tilde{Y}) \oplus H_{k} (\tilde{N}) \overset{\tilde{p_{k}}}{⟶} H_{k} (\tilde{X_{K}}) \overset{\tilde{δ_{k}}}{⟶} \dots (k \in Z)$
$\tilde{Y} \cap \tilde{N}$ は連結であったので $\tilde{j_{0}}$ は単射である．よって $Im \tilde{j_{1}}$ を計算することによって $H_{1} (\tilde{X_{K}})$ が求まる．

そこで $H_{1} (\tilde{Y} \cap \tilde{N}) = ⟨ a_{i}^{+}, b_{i}^{-} | i \in Z ⟩$ の生成元の行き先を議論しよう．

$\tilde{X_{K}}$ の構成を思い出すと，貼り合わせは以下のように行っていた．

次のペア $(1)$ $Y_{i}$ と $N_{i}$ $(2)$ $Y_{i + 1}$ と $N_{i}$ を以下のようにして貼り合わせます．

$Y_{i}$ と $N_{i}$ は共通部分 $N_{i}^{+}$ を自然に同一視することで貼り合わせる．
$Y_{i + 1}$ と $N_{i}$ は，それぞれの部分集合である $N_{i + 1}^{-}$ と $N_{i}^{-}$ を自然に同一視することで貼り合わせる．

すると，全ての $i \in Z$ で貼り合わせて得られる空間は $\tilde{X_{K}}$ となります．

そこで次のような自然な埋め込みによって $\tilde{j_{1}}$ の像を指定する(添え字の行き先を指定している)．
$N_{i}^{+} ↪ Y_{i} or N_{i}, N_{i}^{-} ↪ Y_{k + 1} or N_{i}$
また，命題7の証明で登場した群準同型 $j_{1} : H_{1} (Y \cap N) \to H_{1} (Y) \oplus H_{1} (N)$ の像は以下の通りだった．

$\begin{array}{r} {\begin{cases} j_{1} (a^{+}) = m α + β + a, \\ j_{1} (b^{+}) = β + b, \end{cases} {\begin{cases} j_{1} (a^{-}) = m α + a, \\ j_{1} (b^{-}) = α + β + b, \end{cases} j_{1} (γ) = γ_{Y} + γ_{N} . \end{array}$

よって $2$ つの議論を併せることにより， $\tilde{j_{1}} : H_{1} (\tilde{Y} \cap \tilde{N}) \to H_{1} (\tilde{Y}) \oplus H_{1} (\tilde{N})$ の像は以下のようになる．

$\begin{array}{r} {\begin{cases} \tilde{j_{1}} (a_{i}^{+}) = m α t^{i} + β t^{i} + a t^{i}, \\ \tilde{j_{1}} (b_{i}^{+}) = β t^{i} + b t^{i}, \end{cases} {\begin{cases} \tilde{j_{1}} (a_{i}^{-}) = m α t^{i + 1} + a t^{i}, \\ \tilde{j_{1}} (b_{i}^{-}) = α t^{i + 1} + β t^{i + 1} + b t^{i}, \end{cases} (i \in Z) . \end{array}$
(貼り合わせによる添え字の変化に注意)

次に剰余加群 $H_{1} (\tilde{Y}) \oplus H_{1} (\tilde{N}) / Im \tilde{j_{1}}$ の $Λ$ 加群としての表示を考える． $\tilde{j_{1}} (b_{i}^{+}) = 0$ と $\tilde{j_{1}} (a_{i}^{-}) = 0$ より $a, b$ は $a = - m α t, b = - β$ と表される．よって $\tilde{j_{1}} (a_{i}^{+}) = 0$ と $\tilde{j_{1}} (b_{i}^{-}) = 0$ に代入することで次を得る．
$m α + β - m α t = 0, (α + β) t - β = 0.$
前者の式を変形して $β = (t - 1) m α$ とし，後者の式へ代入することで次を得る．
$\begin{array}{r} (α + (t - 1) m α) t - (t - 1) m α = 0 ⟺ (m t^{2} + (1 - 2 m) t + m) α = 0. \end{array}$

よって $K = J (2, 2 m)$ のAlexander加群 $H_{1} (\tilde{X_{K}})$ は
$\begin{aligned} H_{1} (\tilde{X_{K}}) & ≃ H_{1} (\tilde{Y}) \oplus H_{1} (\tilde{N}) / Im \tilde{j_{1}} \\ ≃ ⟨ α ⟩_{Λ} / ((m t^{2} + (1 - 2 m) t + m) α) ≃ Λ / (m t^{2} + (1 - 2 m) t + m) . \end{aligned}$
となり計算が完了した．

ツイスト結び目 $J (2, 2 m)$ のAlexander多項式は $Δ_{J (2, 2 m)} (t) = m t^{2} + (1 - 2 m) t + m$ となる．

応用：Alexander多項式が自明となる結び目たち

今回の計算結果は，「より一般のツイスト結び目」である二重化結び目へ拡張することが可能です．簡単ではありますがdoubled knotについて紹介します．

サテライト結び目

$C$ を $S^{3}$ 内の結び目， $P$ をソリッドトーラス $S^{1} \times D^{2}$ 内の結び目とする．
$C$ の正則近傍 $N = N (C)$ はソリッドトーラスであるので，同相写像 $ϕ : S^{1} \times D^{2} \to N$ をとる．
このとき， $S^{3}$ 内の結び目 $K = ϕ (P)$ を $C$ をコンパニオン， $P$ をパターンとしたサテライト結び目という．

上のサテライト結び目の定義は同相写像 $ϕ$ に依っています．そこで $ϕ$ に関する整数値を定めます．

$p, q$ を $D^{2}$ の異なる $2$ 点とし， $P := S^{1} \times {p}, Q := S^{1} \times {q}$ をそれぞれ $S^{1} \times D^{2}$ 内の結び目とします．このとき $ϕ (P)$ と $ϕ (Q)$ の絡まり数を $ϕ$ の捻じれ数(twisting number)と呼ぶことにしましょう．すると次のことが知られています．

サテライト結び目は $ϕ$ の捻じれ数によって一意的に定まる．

二重化結び目

それでは二重化結び目を定義しましょう．ソリッドトーラスに埋め込まれた次のような結び目 $K_{0}$ を考えます．

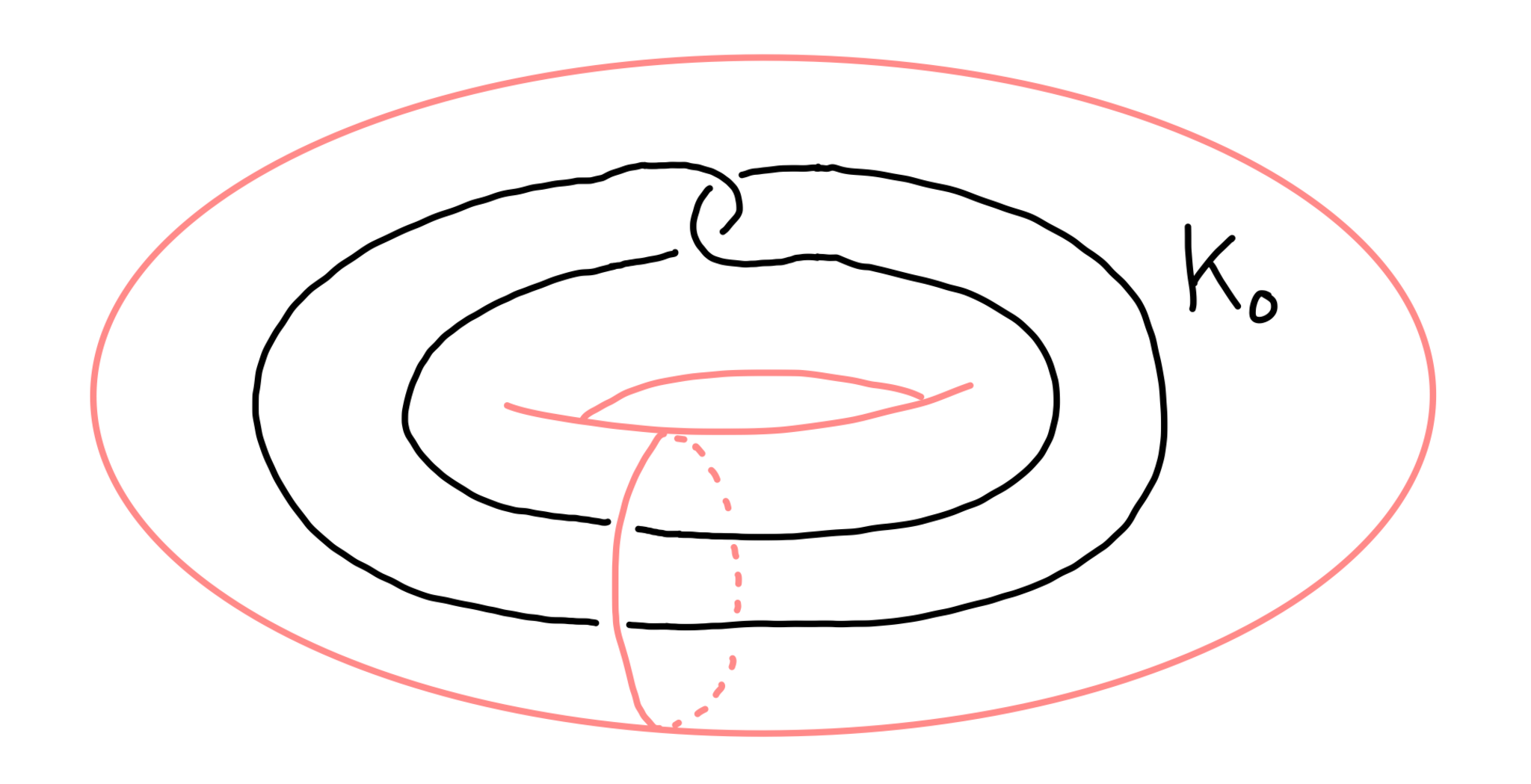ソリッドトーラスに埋め込まれた結び目

上の結び目 $K_{0}$ をパターンとしたサテライト結び目を二重化結び目(doubled knot)という．

次の結び目(の図式)は，三葉結び目をコンパニオンとした捻じれ数 $m = 0$ の二重化結び目です．捻じれ数は見た目のイメージと一致しないことが多いため注意が必要です．

二重化結び目

捻じれ数 $m$ の二重化結び目 $K$ について，Alexander多項式はツイスト結び目 $J (2, 2 m)$ と一致する．
$Δ_{K} (t) = m t^{2} + (1 - 2 m) t + m .$

概略

コンパニオンの結び目に依らないことを確かめるには，ソリッドトーラス $S^{1} \times D^{2}$ のロンジチュードの像である $K^{'} := ϕ (P)$ が結び目補空間 $X_{K}$ においてヌルホモロガスであればよい．

$m = 0$ のとき $K$ と $K^{'}$ の絡まり数は $0$ である．よって $K^{'}$ は $X_{K}$ 内においてSeifert曲面を張る．即ちホモロジー群のバウンダリーとなっているため $K^{'}$ はヌルホモロガスである．

$m \neq 0$ のときについても，パターンをツイスト結び目 $J (2, 2 m)$ に対応するものと交換することで， $K$ はサテライト結び目として捻じれ数 $0$ であるとして議論が可能である．よって同様にしてコンパニオンの結び目に依らないことが分かる．

特にAlexander多項式は $t^{i}$ 倍 ( $i \in Z$ )の差を除いて結び目の不変量であったので，次を得ます．

捻じれ数 $m = 0$ の二重化結び目 $K$ について，Alexander多項式は自明である．
$Δ_{K} (t) = 1.$

あとがき

最後まで読んでいただきありがとうございました．hyqutです．

今回のテーマである「Alexander多項式」は，今年(2021年)の8月からRolfsen[1]を読んで勉強を開始しました．本来のモチベーションは，夏休みの読書感想文としてRolfsenを読み終えたいと考えており，特に「 $3$ 次元多様体の手術」を勉強する予定でした．が，その章の手前にあるAlexander多項式の解説で足踏みを続け，その過程でいろいろな計算方法と出会うことができ，そして今回の記事作成と相成りました．

私の専門は「曲面結び目」という分野なのですが，今回のAlexander多項式の定義は(向き付け可能な)曲面結び目に対して同様の定義が可能となっています．さらに高次の結び目についても拡張ができるらしいです．すごいです．曲面結び目の不変量というのは知られているものがまだ少なく，またJones多項式のように計算が可能なものというのは知っているものでも数えられる程度しかありません．そのため，このAlexander多項式の勉強が結果として新たな曲面結び目の不変量の勉強につながったのは，ラッキーでした．

このあとがきを書いている最中に，定理14の一般論は知られていないのか気になり，調べてみると次の定理が成り立つそうです（[5]-命題8.23）．

$P$ をパターン， $C$ をコンパニオンとする捻じれ数 $m$ のサテライト結び目 $K$ について，Alexander多項式は
$Δ_{K} (t) = Δ_{P} (t) \cdot Δ_{C} (t^{m})$
となる．ここで， $Δ_{P} (t)$ は自明な結び目をコンパニオンとする捻じれ数 $0$ のサテライト結び目のAlexander多項式である．

この定理の主張を眺める限りでは，捻じれ数 $m = 0$ に帰着させる議論を行うことでトレス条件から $Δ_{C} (1) = 1$ となり確かに証明の方針が正しいことが分かります．やった～．

次回の記事作成については，いつごろから再開するか未定です．気長にお待ちいただければと思います．
最後の最後まで読んでいただきありがとうございました！

参考文献

[1]

Dale. Rolfsen, Knots and links, Mathematics Lecture Series, Publishor Perish, Inc., Houston, TX, 1976

[2]

北野晃朗, 合田洋, 森藤孝之, ねじれアレキサンダー不変量, 数学メモアール第5巻, 日本数学会, 2006

[3]

村上順, 結び目理論:分解定理・不変量・体積予想, 森北出版, 2021

[4]

Jessica Purcell, Hyperbolic Knot Theory, Graduate Studies in Mathematics, Amer Mathematical Society, 2020

[5]

Gerhard Burde, Heiner Zieschang, Knots, de Gruyter Studies in Mathematics 5, De Gruyter, 2013

投稿日：2021年9月30日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

hyqut

5186

専攻：低次元トポロジー

他の人のコメント

コメントはありません。

読み込み中

hyqut

結び目のAlexander多項式を計算したい① 結び目補空間のホモロジー群による計算

はじめに
参考文献について
結び目補空間からAlexander不変量の構成
結び目のAlexander加群
諸々の性質とAlexander多項式
本記事で計算したいツイスト結び目のAlexander加群は，幸運なことに単項イデアルによる剰余加群と同型になることが(結果的に)分かります．そこで，次章ではホモロジー群を用いてAlexander多項式の計算を行います．
計算パート
無限巡回被覆空間$\widetilde{X_K}$の具体的な構成
以上により，結び目$K$のSeifert曲面$F$を指定することで$\widetilde{X_K}$の分解を与えることができます．
Seifert曲面と各種ホモロジー群の生成元
本題へ取り組む前の練習問題 : $H_1(X_K) \simeq \Z$
ツイスト結び目のAlexander不変量
応用：Alexander多項式が自明となる結び目たち
サテライト結び目
二重化結び目
あとがき
参考文献

結び目のAlexander多項式を計算したい① 結び目補空間のホモロジー群による計算

はじめに

参考文献について

結び目補空間からAlexander不変量の構成

結び目のAlexander加群

諸々の性質とAlexander多項式

本記事で計算したいツイスト結び目のAlexander加群は，幸運なことに単項イデアルによる剰余加群と同型になることが(結果的に)分かります．そこで，次章ではホモロジー群を用いてAlexander多項式の計算を行います．

補足: Alexanderの双対定理

計算パート

無限巡回被覆空間XK~の具体的な構成

以上により，結び目KのSeifert曲面Fを指定することでXK~の分解を与えることができます．

Seifert曲面と各種ホモロジー群の生成元

本題へ取り組む前の練習問題 : H1(XK)≃Z

ツイスト結び目のAlexander不変量

応用：Alexander多項式が自明となる結び目たち

サテライト結び目

二重化結び目

あとがき

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

無限巡回被覆空間 $\tilde{X_{K}}$ の具体的な構成

以上により，結び目 $K$ のSeifert曲面 $F$ を指定することで $\tilde{X_{K}}$ の分解を与えることができます．

本題へ取り組む前の練習問題 : $H_{1} (X_{K}) ≃ Z$