(0,1)とRの対応

$f (x) = \frac{1}{1 - x} - \frac{1}{x}$ とする

$f : (0, 1) \to R$ は全単射

$f^{'} (s) = \frac{1}{x^{2}} + \frac{1}{(1 - x)^{2}} > 0$ なので $f$ は単射
$f$ は連続かつ $lim_{x \to 0} f (x) = - \infty$ かつ $lim_{x \to 1} f (x) = \infty$ なので全射

ちなみに逆写像は汚くて $f^{- 1} (y) = \frac{\sqrt{y^{2} + 4} + y - 2}{2 y}$

追記: google charts で描いてみた
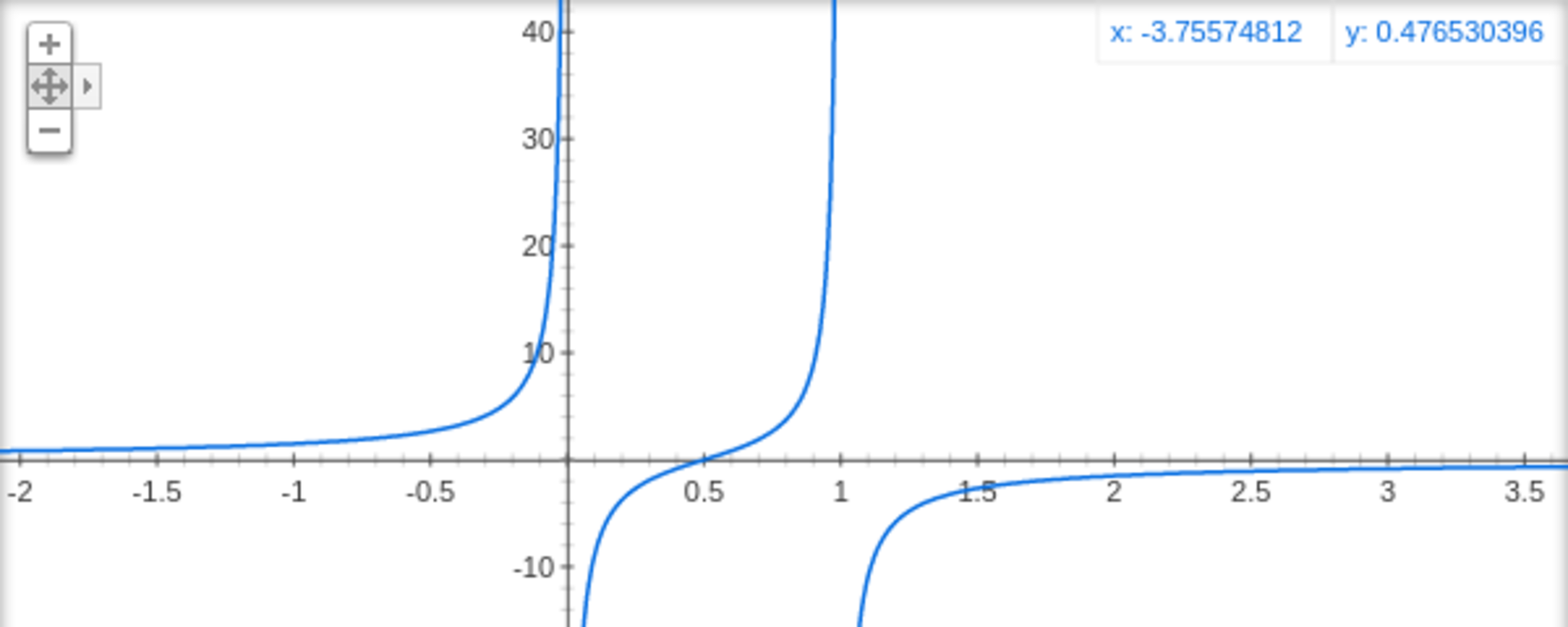1/(1-x)-1/x

投稿日：2021年10月15日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

usagiop

1439

他の人のコメント

コメントはありません。

読み込み中

usagiop

(0,1)とRの対応