ε-δ論法を図示する

311

極限の定義

$lim_{x \to a} f (x) = b$
$\Leftrightarrow (\forall ε > 0, \exists δ > 0 s . t . | x - a | < δ \Rightarrow | f (x) - b | < ε)$

訳すと

「どんな $ε > 0$ に対してでも、 $| x - a | < δ \Rightarrow | f (x) - b | < ε$ となるような $δ > 0$ が存在する。」
となります。

関数 $f (x)$ があり、 $y = f (x)$ からどんな距離の点を $f (x)$ 上でとったとしても、その点の $x$ 座標と $x = a$ との距離が必ず $δ$ より小さくなる、というような $δ$ が存在する

ということを言っており、図示するとこのようになります。

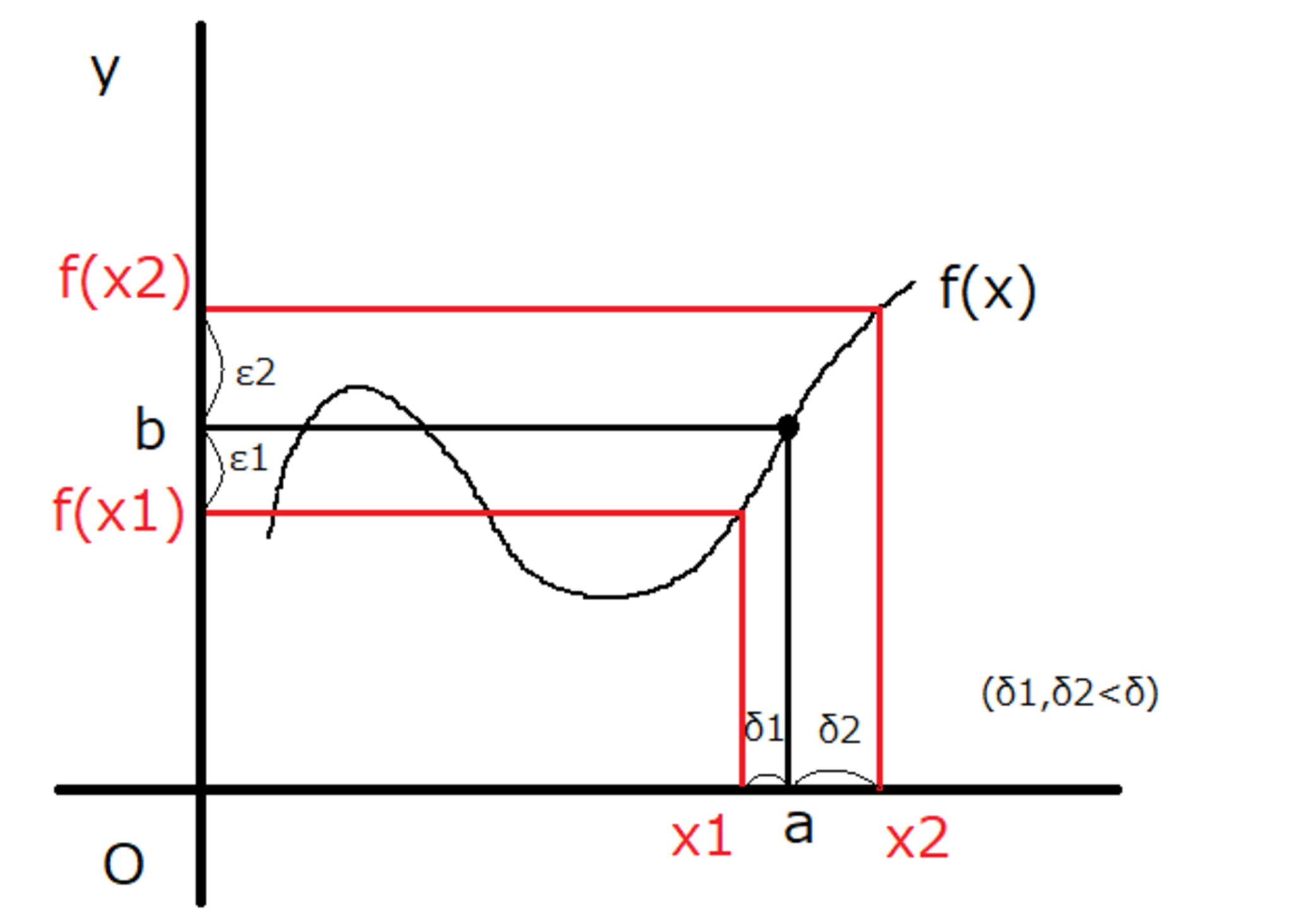ε-δ論法を図示

まず、 $f (x_{1})$ と $b$ の距離が $ε_{1}$ となるような $x_{1}$ を設定してみます。

すると、 $| x_{1} - a | < δ_{1}$ となります。

次に、 $f (x_{2})$ と $b$ の距離が $ε_{2}$ となるような $x_{2}$ を設定してみます。

すると、 $| x_{2} - a | < δ_{2}$ となります。

これを繰り返していき、どんな $ε$ を設定しても、 $| x - a | < δ$ となる $δ$ が見つかれば $lim_{x \to a} f (x) = b$ だよー、と言っています。

関数 $f (x) = x (x \neq 0)$ があり、 $f (0)$ は存在しないものとします。
$\forall ε > 0, δ = ε$ とおくと
$| x - 0 | < δ$
$\Rightarrow | f (x) - 0 | = | x - 0 | < δ = ε$
よって、 $\forall ε > 0, \exists δ > 0 s . t . | x - 0 | < δ \Rightarrow | f (x) - 0 | < ε$ となり
$lim_{x \to 0} f (x) = 0$ といえます。

ポイントは、 $δ$ を $ε$ を使ってうまく設定することです。

連続性

$関数 f (x) が区間 I で連続$
$\Leftrightarrow (\forall ε > 0, \forall a, x \in I, \exists δ > 0 s . t . | x - a | < δ \Rightarrow | f (x) - f (a) | < ε)$

上記の図で $b = f (a)$ となる場合です。

やっていることは同じです。

関数 $f (x) = x^{2}$ がある。
$\forall a \in R, \forall ε > 0$
$δ = \frac{ε}{| x + a |}$ とおくと
$| x - a | < δ = \frac{ε}{| x + a |}$
$| x - a | | x + a | < ε$

$| x - a | < δ$
$\Rightarrow | f (x) - f (a) | = | x^{2} - a^{2} | = | x - a | | x + a | < ε$

よって、 $\forall ε > 0, \forall a, x \in R, \exists δ > 0 s . t . | x - a | < δ \Rightarrow | f (x) - f (a) | < ε$ となり
$f (x) = x^{2}$ は連続といえます。

2023/1/25 追記

申し訳ないのですが、アライグマ様からコメントで訂正をいただきました。
言葉を雑に扱っていたことを反省し、精進します。

$lim_{x \to a} f (x) = b$
$\Leftrightarrow (\forall ε > 0, \exists δ > 0 s . t . 0 < | x - a | < δ \Rightarrow | f (x) - b | < ε)$

$0 <$ を加えることで、 $x = a$ の場合を除外しました。

点 $a$ に限りなく近づく、ということなので $x = a$ の場合を除外します。

ちなみに、点 $x = a$ を許した場合が連続の定義となります。

$「 lim_{x \to a} f (x) = f (a) \Rightarrow f (x) は点 a で連続」$
ということを理解していればイメージしやすいと思います。
(僕はイメージできていなかったゆえに間違えておりました。)

$I = (b, c) \subseteq R を空でない開区間, f (x) を I 上で定義された実数値関数, a \in I とする .$
$このとき, f (x) が x = a で連続であるとは, 次の条件を満たすことである :$
$\forall ε > 0, \exists δ > 0 s . t . \forall x \in I (| x - a | < δ \Rightarrow | f (x) - f (a) | < ε)$

間違い
$\forall ε > 0, \forall a, x \in I, \exists δ > 0 s . t . | x - a | < δ \Rightarrow | f (x) - f (a) | < ε$
$「 . . . \forall a, x \in I s . t . . . . 」$ とあるので、「 $| x - a | < δ \Rightarrow | f (x) - f (a) | < ε$ 」を評価する前に、 $x$ と $a$ を最初に設定できます。
この $x, a$ に対して $δ = \frac{| x - a |}{2}$ とおくことで
「 $| x - a | < δ \Rightarrow | f (x) - f (a) | < ε$ 」は必ずTRUEになります。

( $| x - a | < \frac{| x - a |}{2}$ 　はFALSEで、「FALSE⇒TRUE」「FALSE⇒FALSE」はどちらもTRUEとなります。例えば「明日は晴れ ⇒ 運動会を決行する」は「明日が雨」のときについては言っていないので、雨の時に決行しようがしまいがウソは言っていません。)