文献あり

準同型定理

1224

方針

　準同型定理を捉え直していこうと思います。加群で話は進めますが、群でも環でも同様な議論はできます。
　方針としては剰余加群を特徴づける性質を用いて議論を進めていこうと思います。

普遍性

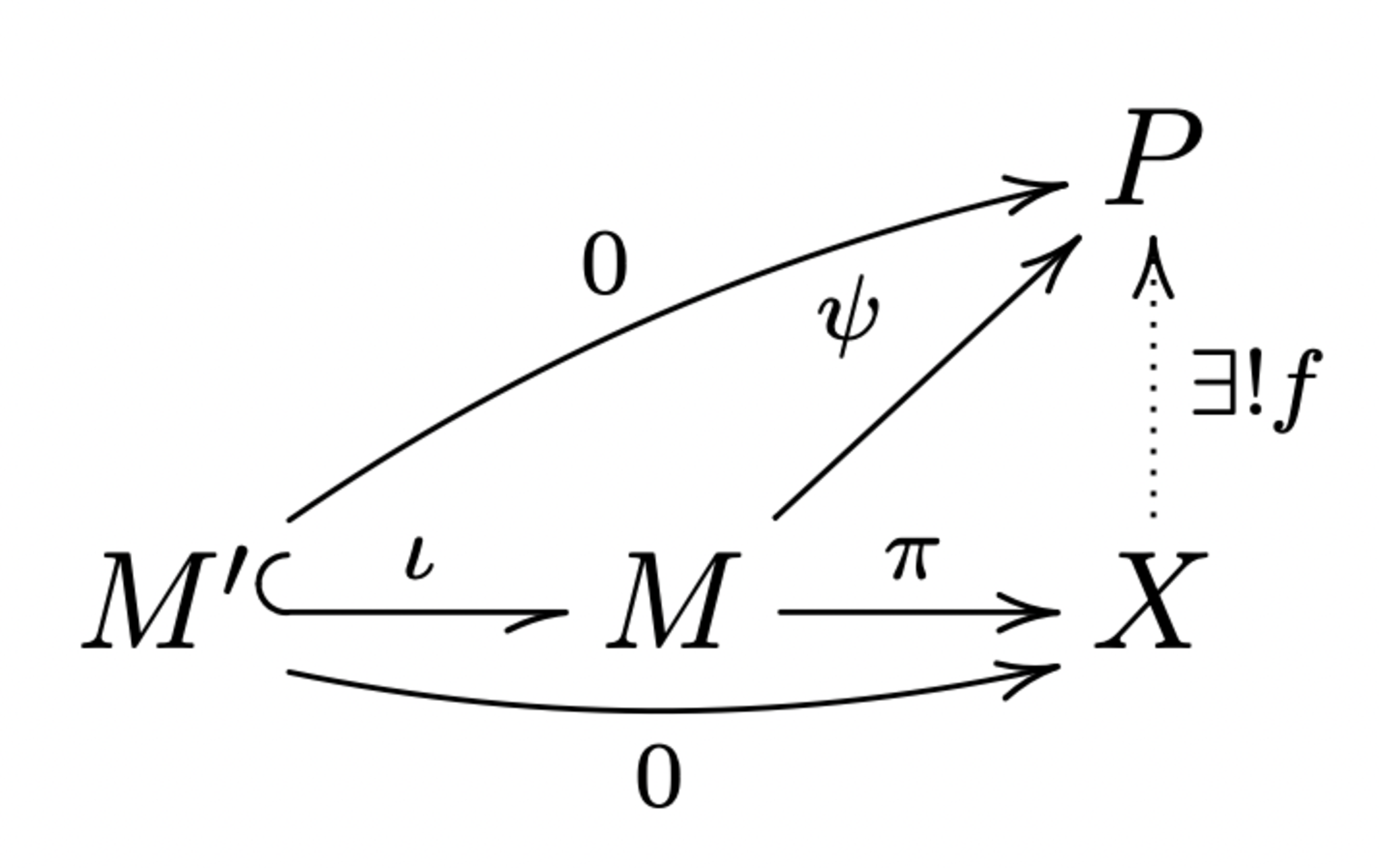
　$M$を加群、$M'$を$M$の部分加群、$\iota :M'\hookrightarrow M$を包含写像とします。この時、加群$X$と全射準同型$\pi:M\rightarrow X$で、$x-y\in M' \Leftrightarrow \pi(x) = \pi(y)$を満たすものを考えます($X=M/M',\pi$は自然な全射が念頭にあります...)。特に、$\pi \circ \iota = 0$となります。

上記で定義した$(X,\pi)$は次のような普遍性を持つ. 任意の加群と準同型の組$(P,\psi)$で、$\psi:M\rightarrow P$かつ$\psi \circ\iota=0$なるものに対し、準同型$f:X\rightarrow P$であり$f\circ \pi = \psi$を満たすものが一意的に存在する.
可換図式

　$f$の存在については$f(\pi(x))=\psi(x)$と定めた$f$がwell-definedであることから分かる。実際、$\pi(x)=\pi(y)$ならば$x-y\in M'$なので、$\psi \circ\iota=0$より$\psi(x)=\psi(y)$. よって$f$はwell-defined.
　$f$の一意性は$\pi$が全射であることから$\pi(x)$は$f$の定義域を隈なく動くことから分かる.
　$\psi,\pi$が準同型なので$f$も準同型.

　この普遍性を満たす$X$は同型を除いて一意であることは直ちに分かります。

命題１の

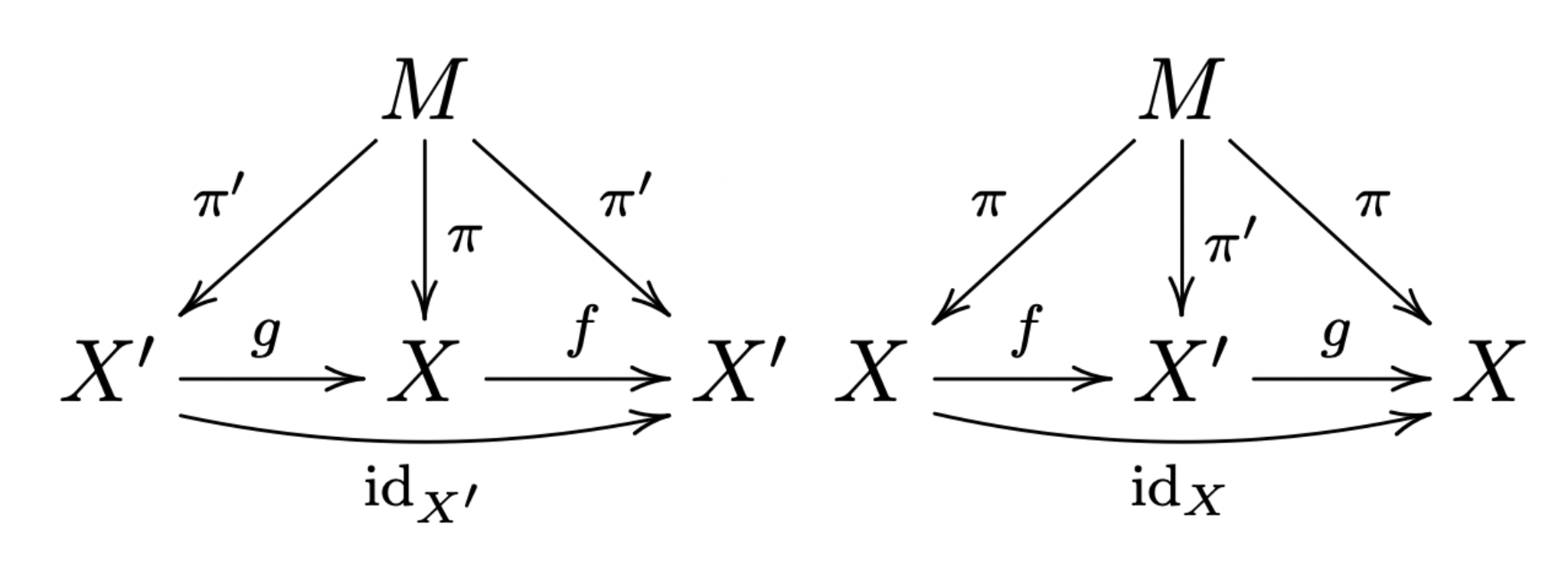
$(X,\pi),(X',\pi')$が共に命題１の普遍性を満たすならば、$X\cong X'$

　任意の$(P,\psi)$を$(X,\pi)$や$(X',\pi')$にすると下記のような可換図式が書ける.

可換図式２

　写像の一意性から$f \circ g=\rm{id}_{X'}$かつ$g\circ f=\rm{id}_X$である. ゆえに$f$は同型写像であるため、$X\cong X'$.

準同型定理

　では本題に入っていこうと思います。まずこのような$(X,\pi)$の具体的な構成としては、剰余加群(剰余群、剰余環でも同様)$M/M'$を考えればよいです。$\pi:M\rightarrow M/M'$は自然な全射準同型です。ゆえに、系が言っていることは剰余加群の普遍性を持つものは同型を除いて一意であるということです。
　$f:M\rightarrow N$を準同型とします。ここで、$X$として$\rm{Im} $$f,\pi$として$f|_N$($f$の制限、値域を$\rm{Im} $$f$にしたもの)を考えてみましょう。もちろん$f|_N$は全射準同型になります。$\rm{Im}$$f$が命題１の普遍性を満たすためには$M'$をどのようにとってくる必要があるでしょうか。
　$x-y\in M' \Leftrightarrow f|_N(x) = f|_N(y)$を睨んでみると、この性質は$M'=$$\rm{Ker}$$f$を示唆しているように見えます!!!!　まとめます。

準同型定理

$f:M\rightarrow N$を加群の準同型とする.この時、$M/\rm{Ker}$$f\cong$$\rm{Im}$$f$が成り立つ.

　$\pi:M\rightarrow M/ \rm{Ker}$$f$を自然な全射準同型、$f|_N:M\rightarrow \rm{Im}$$f$を$f$の制限とする.
この時、$x-y\in \rm{Ker}$$f$$\Leftrightarrow\pi(x)=\pi(y) \Leftrightarrow f|_N(x) = f|_N(y)$である.ゆえに、$(M/\rm{Ker}$$f,\pi)$と$(\rm{Im}$$f,f|_N)$はどちらも命題１の普遍性を満たす.よって、系より$M/\rm{Ker}$$f\cong\rm{Im}$$f$.