対角化とスペクトル分解

はじめに

この記事は Wathematica Advent Calender 2021 の12/14の記事です．

この記事のメインテーマは「行列の対角化」です．

固有方程式$\det (\lambda \mathbf{I}-\mathbf{A})=0$を解いて，固有空間$E_{\lambda }(\mathbf{A})=\{\mathbf{x}\in {\mathbb{R}}^n|\mathbf{A}\mathbf{x}=\lambda \mathbf{x}\}$の基底を見つけて，基底を並べて行列$\mathbf{P}=[\begin{array}{ccc}{\mathbf{p}}_1& \cdots & {\mathbf{p}}_n\end{array}]$を作って……っていう流れを叩き込まれるのが，B1の線型代数だと思います（個人の感想です）．このへんの数学的なしくみについては， 同期の記事 に詳しく載っています．

この記事では，その図形的な意味と，それを踏まえた応用の話をしてみようと思います．

対角化

まず，$2\times 2$行列を例にとって，対角化について考察しましょう．$2\times 2$実行列$\mathbf{A}$に対し，$\mathbf{\Lambda }={\mathbf{P}}^{-1}\mathbf{A}\mathbf{P}$が対角行列になるような実行列$\mathbf{P}$が存在するとします．このとき，$\mathbf{P}=[\begin{array}{cc}{\mathbf{p}}_1& {\mathbf{p}}_2\end{array}]$とおくと$\mathcal{B}=\{{\mathbf{p}}_1,{\mathbf{p}}_2\}$は${\mathbb{R}}^2$の基底なので，任意のベクトル$\mathbf{x}=[\begin{array}{cc}x& y\end{array}{]}^{\mathsf{T}}\in {\mathbb{R}}^2$は
$$\mathbf{x}=s{\mathbf{p}}_1+t{\mathbf{p}}_2=\mathbf{P}\left[\begin{array}{c}s\\ t\end{array}\right]\text{(}s,t\in \mathbb{R}\text{)}$$
と一意に表せます．$s$と$t$は上の式から$[\begin{array}{cc}s& t\end{array}{]}^{\mathsf{T}}={\mathbf{P}}^{-1}\mathbf{x}$と求められます．

これは，${\mathbf{P}}^{-1}$を左から掛けると，$xy$座標から$st$座標へと座標系を取り換えられることを意味します．たとえば$\mathbf{P}=[\begin{array}{cc}3& 1\\ 1& 3\end{array}]$，$\mathbf{x}=[\begin{array}{cc}7& 5\end{array}{]}^{\mathsf{T}}$のときは$\mathbf{x}=2{\mathbf{p}}_1+{\mathbf{p}}_2$なので，次図のようになります．

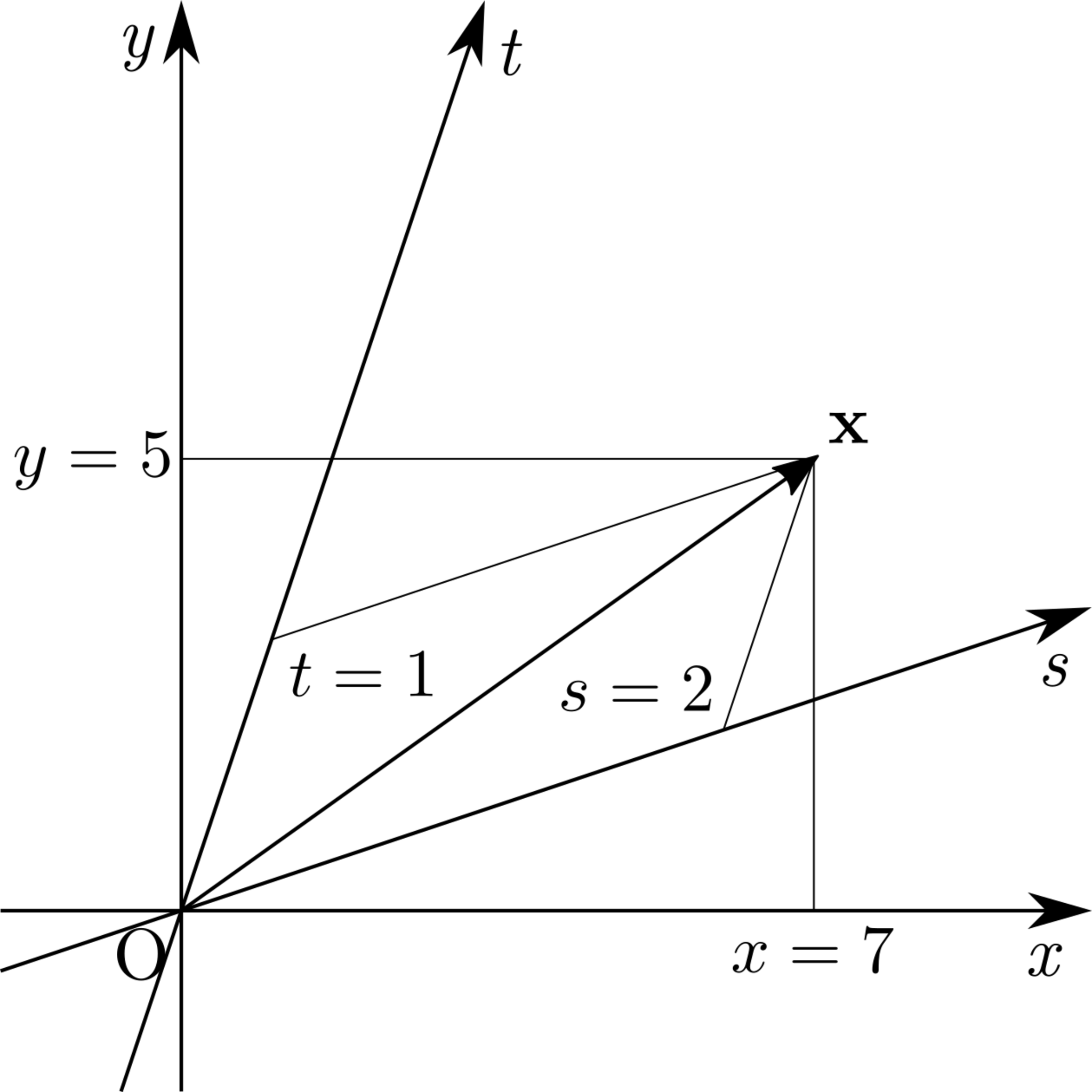xy座標とst座標の関係

逆に，$\mathbf{P}$を左から掛ければ，$st$座標から$xy$座標へと座標系を取り替えられます．よって，$\mathbf{x}$に行列$\mathbf{A}=\mathbf{P}\mathbf{\Lambda }{\mathbf{P}}^{-1}$を左から掛けると，$\mathbf{x}$は次のように変形されます．

1. まず${\mathbf{P}}^{-1}$が掛けられることで，$\mathbf{x}$が$st$座標で表わされる
2. 次に$\mathbf{\Lambda }$が掛けられることで，$s$軸方向に$\mathbf{\Lambda }$の$(1,1)$成分${\lambda }_1$倍，$t$軸方向に$\mathbf{\Lambda }$の$(2,2)$成分${\lambda }_2$倍だけ拡大される
3. 最後に$\mathbf{P}$が掛けられることで，$\mathbf{x}$が$xy$座標に戻される

以上をまとめると，対角化できる行列においては，行列をベクトルに掛ける操作が「ある座標系において各軸向きに拡縮する」という操作と同等になります．

スペクトル分解

前節では「対角化できる行列においては，行列をベクトルに掛ける操作が『ある座標系において各軸向きに拡縮する』という操作と同等になる」ということを見ました．ここではそれを踏まえて，対角化を別の形で表記してみましょう．

まず，$[\begin{array}{cc}s& t\end{array}{]}^{\mathsf{T}}={\mathbf{P}}^{-1}\mathbf{x}$だったので，$({\mathbf{P}}^{-1}{)}^{\mathsf{T}}=[\begin{array}{cc}{\mathbf{q}}_1& {\mathbf{q}}_2\end{array}]$とおくと
$$\left[\begin{array}{c}s\\ t\end{array}\right]=\left[\begin{array}{c}{\mathbf{q}}_1^{\mathsf{T}}\\ {\mathbf{q}}_2^{\mathsf{T}}\end{array}\right]\mathbf{x}=\left[\begin{array}{c}{\mathbf{q}}_1^{\mathsf{T}}\mathbf{x}\\ {\mathbf{q}}_2^{\mathsf{T}}\mathbf{x}\end{array}\right],\therefore s={\mathbf{q}}_1^{\mathsf{T}}\mathbf{x},t={\mathbf{q}}_2^{\mathsf{T}}\mathbf{x}$$
となります．よって，次式が成立します．
$$\mathbf{x}=s{\mathbf{p}}_1+t{\mathbf{p}}_2=({\mathbf{q}}_1^{\mathsf{T}}\mathbf{x}){\mathbf{p}}_1+({\mathbf{q}}_2^{\mathsf{T}}\mathbf{x}){\mathbf{p}}_2$$

ここで，$\mathbf{A}$を掛けると，$\mathbf{x}$は$s$軸方向に${\lambda }_1$倍，$t$軸方向に${\lambda }_2$倍だけ拡大されるので
$$\mathbf{A}\mathbf{x}={\lambda }_{1}s{\mathbf{p}}_1+{\lambda }_{2}t{\mathbf{p}}_2={\lambda }_1({\mathbf{q}}_1^{\mathsf{T}}\mathbf{x}){\mathbf{p}}_1+{\lambda }_2({\mathbf{q}}_2^{\mathsf{T}}\mathbf{x}){\mathbf{p}}_2$$
です．上の式を変形すると
$$\mathbf{A}\mathbf{x}={\lambda }_1({\mathbf{q}}_1^{\mathsf{T}}\mathbf{x}){\mathbf{p}}_1+{\lambda }_2({\mathbf{q}}_2^{\mathsf{T}}\mathbf{x}){\mathbf{p}}_2=({\lambda }_1{\mathbf{p}}_1{\mathbf{q}}_1^{\mathsf{T}}+{\lambda }_2{\mathbf{p}}_2{\mathbf{q}}_2^{\mathsf{T}})\mathbf{x}$$
となり，これが任意の$\mathbf{x}\in {\mathbb{R}}^2$に対して成立するので，$\mathbf{A}={\lambda }_1{\mathbf{p}}_1{\mathbf{q}}_1^{\mathsf{T}}+{\lambda }_2{\mathbf{p}}_2{\mathbf{q}}_2^{\mathsf{T}}$が成り立ちます．

この式は，$\mathbf{P}$が直交行列ならもっと簡単になります．実際，$({\mathbf{P}}^{-1}{)}^{\mathsf{T}}=\mathbf{P}$なら${\mathbf{q}}_1={\mathbf{p}}_1$，${\mathbf{q}}_2={\mathbf{p}}_2$なので，$\mathbf{A}={\lambda }_1{\mathbf{p}}_1{\mathbf{p}}_1^{\mathsf{T}}+{\lambda }_2{\mathbf{p}}_2{\mathbf{p}}_2^{\mathsf{T}}$です．

なぜ$\mathbf{P}$が直交行列のときは${\mathbf{q}}_1$，${\mathbf{q}}_2$が消えるのでしょうか．その理由は，$\mathbf{P}$が直交行列のときは，${\mathbf{p}}_1$と${\mathbf{p}}_2$が正規直交基底をなし，$st$座標が直交座標系になるからです．次の図を見てください．

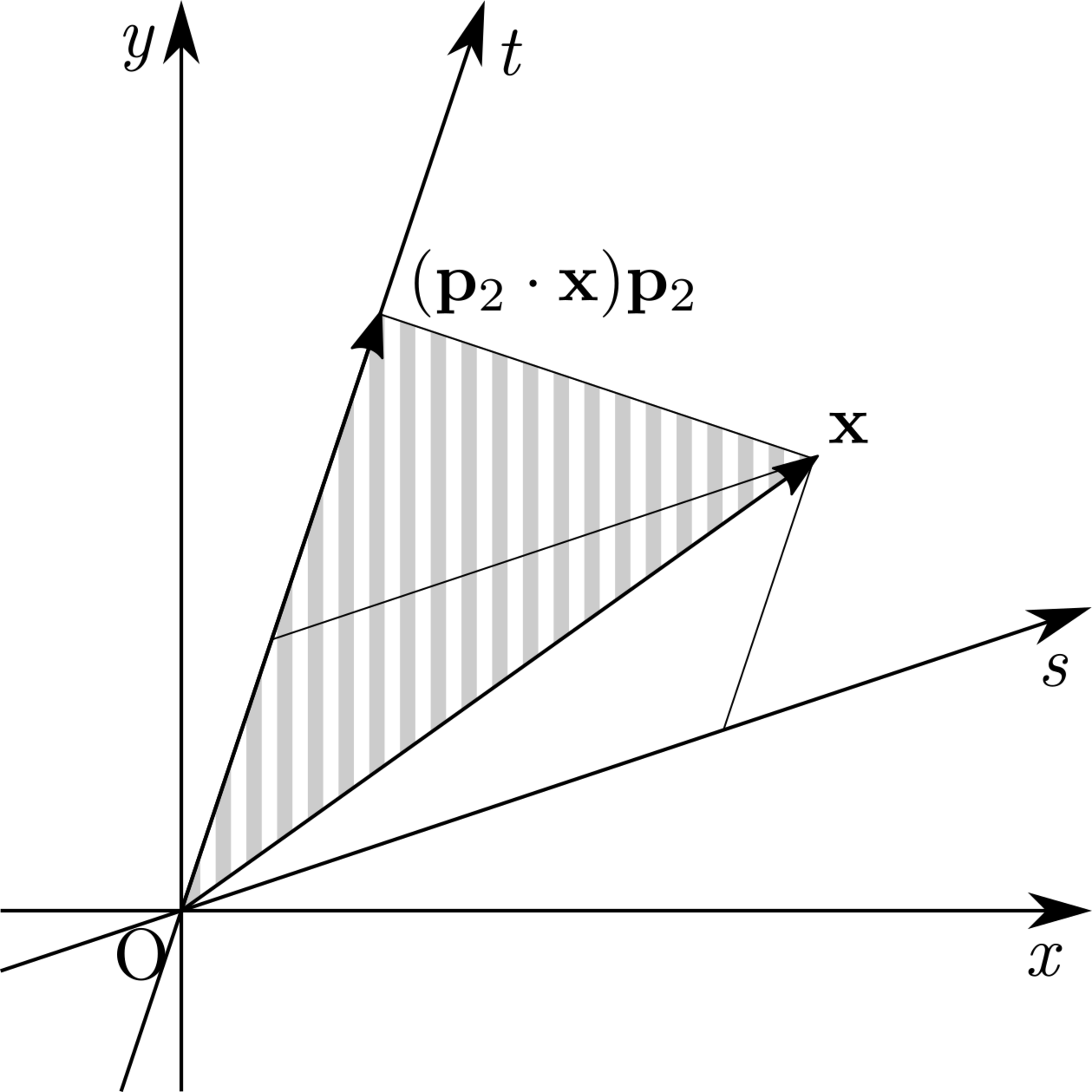st座標が直交座標系でないときの様子

以下では${\mathbf{p}}_1$，${\mathbf{p}}_2$の長さはともに$1$であるとします．このとき${\mathbf{p}}_2^{\mathsf{T}}\mathbf{x}={\mathbf{p}}_2\cdot \mathbf{x}$は，$\mathbf{x}$を${\mathbf{p}}_2$方向へと正射影したベクトルの長さです．よって，図中に縦線で示された三角形は直角三角形です．そして図から，${\mathbf{p}}_1$と${\mathbf{p}}_2$が直交していないときは，$\mathbf{x}$の$t$座標と${\mathbf{p}}_2\cdot \mathbf{x}$は一致しないことが分かります．逆に，${\mathbf{p}}_1$と${\mathbf{p}}_2$が直交していれば，両者は一致します．

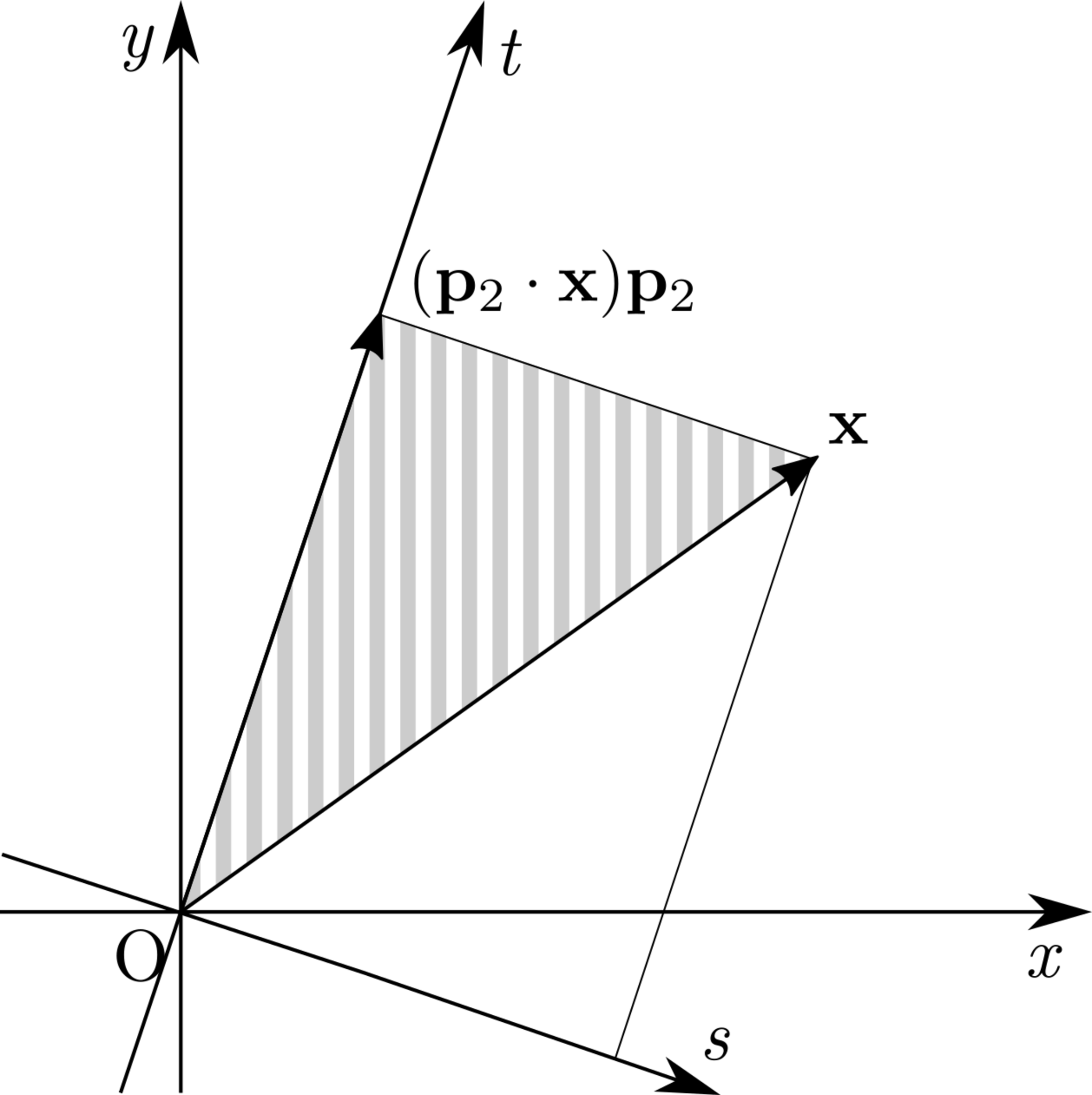st座標が直交座標系であるときの様子

${\mathbf{p}}_1$，${\mathbf{p}}_2$の長さがともに$1$で，かつ直交するとき，$\mathbf{P}$は直交行列になり，その逆も成り立ちます．そのため，$\mathbf{P}$が直交行列であれば，$s$，$t$を計算するのに${\mathbf{q}}_1$，${\mathbf{q}}_2$を定義しなくともよいわけです．

以上の議論は$n$次元で成立します．つまり，$n\times n$実行列$\mathbf{A}$が直交行列$\mathbf{P}=[\begin{array}{ccc}{\mathbf{p}}_1& \cdots & {\mathbf{p}}_n\end{array}]$で対角化されるとき，$\mathbf{\Lambda }={\mathbf{P}}^{-1}\mathbf{A}\mathbf{P}$の$(i,i)$成分を${\lambda }_i$とおくと
$$\mathbf{A}={\lambda }_1{\mathbf{p}}_1{\mathbf{p}}_1^{\mathsf{T}}+\cdots +{\lambda }_n{\mathbf{p}}_n{\mathbf{p}}_n^{\mathsf{T}}$$
が成立します．${\lambda }_1,\dots ,{\lambda }_n$の値がすべて異なるとき，これを$\mathbf{A}$のスペクトル分解といいます（一般の場合については参考文献を参照してください）．

データの要約

ここではスペクトル分解の応用例として，データを要約する手法について説明します．

$n$人の生徒が４科目の試験を受け，次のような結果が得られたとします（この表をそのまま行列とみなしたものを$\mathbf{D}$とします）．

よく勉強している生徒はどの科目もそれなりに良い得点をとると考えられるので，各科目の得点には相関があると考えられます．そこで，各科目の得点を重みづけして足すことで，「総合得点」のような数値を算出できないか考えてみます．より正確には
$$(\text{総合得点})=w_1((\text{国語の得点})-(\text{国語の平均点}))+\cdots +w_4((\text{社会の得点})-(\text{社会の平均点}))$$
となるような$\mathbf{w}=[\begin{array}{ccc}{w}_1& \cdots & w_4\end{array}{]}^{\mathsf{T}}\in {\mathbb{R}}^4$を計算してみます．

まず，定数倍の差を除くため，$\mathbf{w}$の長さは$1$であるという制約を課します．総合得点という変量は要するに，4つの変量を要約した変量ですから，各生徒間での差異が大きければ大きいほど，要約によって情報が失われていないと考えられます．そこで，総合得点の標本分散が最大になるように$\mathbf{w}$を決定しましょう．

$\mathbf{D}$から各科目ごとに平均点を引いた行列を$\mathbf{A}$とおくと，各生徒の総合得点を並べた表は$\mathbf{A}\mathbf{w}$です．また，標本分散$V$は表の2乗和
$$V=\frac{{\left|\mathbf{A}\mathbf{w}\right|}^2}{n}=\frac{{\mathbf{w}}^{\mathsf{T}}{\mathbf{A}}^{\mathsf{T}}\mathbf{A}\mathbf{w}}{n}$$
です．

${\mathbf{A}}^{\mathsf{T}}\mathbf{A}$は$4\times 4$対称行列なので，直交行列で対角化できます．よって，相異なる固有値が$4$個あると仮定すると，${\mathbf{A}}^{\mathsf{T}}\mathbf{A}$は次のようにスペクトル分解できます．
$${\mathbf{A}}^{\mathsf{T}}\mathbf{A}={\lambda }_1{\mathbf{p}}_1{\mathbf{p}}_1^{\mathsf{T}}+\cdots +{\lambda }_4{\mathbf{p}}_4{\mathbf{p}}_4^{\mathsf{T}}$$

また，$\mathcal{B}=\{{\mathbf{p}}_1,\dots ,{\mathbf{p}}_4\}$は${\mathbb{R}}^4$の正規直交基底なので，$\mathbf{w}$は$\mathbf{w}=t_1{\mathbf{p}}_1+\cdots +t_4{\mathbf{p}}_4$とおけます．すると，$\mathcal{B}$の正規直交性から
$$\begin{array}{rl}{\mathbf{A}}^{\mathsf{T}}\mathbf{A}\mathbf{w}& =({\lambda }_1{\mathbf{p}}_1{\mathbf{p}}_1^{\mathsf{T}}+\cdots +{\lambda }_4{\mathbf{p}}_4{\mathbf{p}}_4^{\mathsf{T}})(t_1{\mathbf{p}}_1+\cdots +t_4{\mathbf{p}}_4)\\ & ={\lambda }_1{t}_1{\mathbf{p}}_1+\cdots +{\lambda }_4{t}_4{\mathbf{p}}_4,\\ {\mathbf{w}}^{\mathsf{T}}{\mathbf{A}}^{\mathsf{T}}\mathbf{A}\mathbf{w}& =(t_1{\mathbf{p}}_1^{\mathsf{T}}+\cdots +t_4{\mathbf{p}}_4^{\mathsf{T}})({\lambda }_1{t}_1{\mathbf{p}}_1+\cdots +{\lambda }_4{t}_4{\mathbf{p}}_4)\\ & ={\lambda }_1{t}_1^2+\cdots +{\lambda }_4{t}_4^2\end{array}$$
となります．よって，次式が成立します．
$$V=\frac{{\mathbf{w}}^{\mathsf{T}}{\mathbf{A}}^{\mathsf{T}}\mathbf{A}\mathbf{w}}{n}=\frac{{\lambda }_1{t}_1^2+\cdots +{\lambda }_4{t}_4^2}{n}$$

${\lambda }_1,\dots ,{\lambda }_4$はすべて異なると仮定しているので，${\lambda }_i=max\{{\lambda }_1,\dots ,{\lambda }_4\}$となる$i\in \{1,\dots ,4\}$は一意に定まります．また，$\mathcal{B}$は正規直交基底なので$\left|\mathbf{w}\right|=1⟺t_1^2+\cdots +t_4^2=1$です．よって，上の式から$V$の値が最大になるのは
$$t_k=\{\begin{array}{ll}1& \text{(}k=i\text{)},\\ 0& \text{(}k\ne i\text{)}\end{array}$$
のときであることが分かります．このとき$\mathbf{w}={\mathbf{p}}_i$なので，$V$の値が最大になるような重み$\mathbf{w}$は$\mathbf{w}={\mathbf{p}}_i$です．

以上から，総合得点は${\mathbf{A}}^{\mathsf{T}}\mathbf{A}$をスペクトル分解することで求められることが分かりました．実は，この手法をより発展させると「主成分分析」という手法に繋がります（詳しくは参考文献を参照してください）．