4回回転対称性の拡張
本記事は 日曜数学 Advent Calender 2021 の16日目として書かれています．
回転対称性
我々が図形を見て感じる対称性にはいくつか種類があります．まず，それらを意識的に捉えて議論するには共通する特徴に着目しましょう．それは「ある操作を施しても形が不変であること」です．
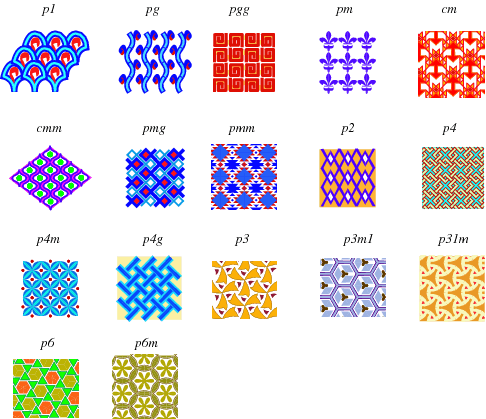Wolfram MathWorldより
その観点に立って，例えば代表的な対称性である回転対称を定義すると次のようになります．
$n$を自然数とする．
平面図形$D$が$n$回対称であるとは，ある点$P$が存在して$P$を中心とする$ \frac{2\pi}{n} $回転について$D$が不変であることをいう．
さて，今回考えたいのはグラデーションをもって対称性を捉えることです．上の定義にもとづけば，図形に対して対称性は「あるかないか」という二値で判断することになります．しかしながら，現実世界では「対称っぽい」と感じるものも多くあります．こういった対象についても感覚のみに頼らない議論をしたいというモチベーションが湧きます．
そこで今回は，凸図形に対する$4$回対称性を取り上げ，「$4$回対称性への近さ」を新たな尺度として定義しようという試みを紹介します．
ある自作パズル
考える契機となったのは次の自作パズルです．
ユークリッド平面上に有界閉凸領域$D$と直線$l$がある．ただし，$D$の面積は$0$でないとする．
$l$によって$D$が面積の等しい$2$つの領域$D_1,D_2$に分けられているとき，$D_1,D_2$の面積を同時に2等分する直線がただ一つ存在する．
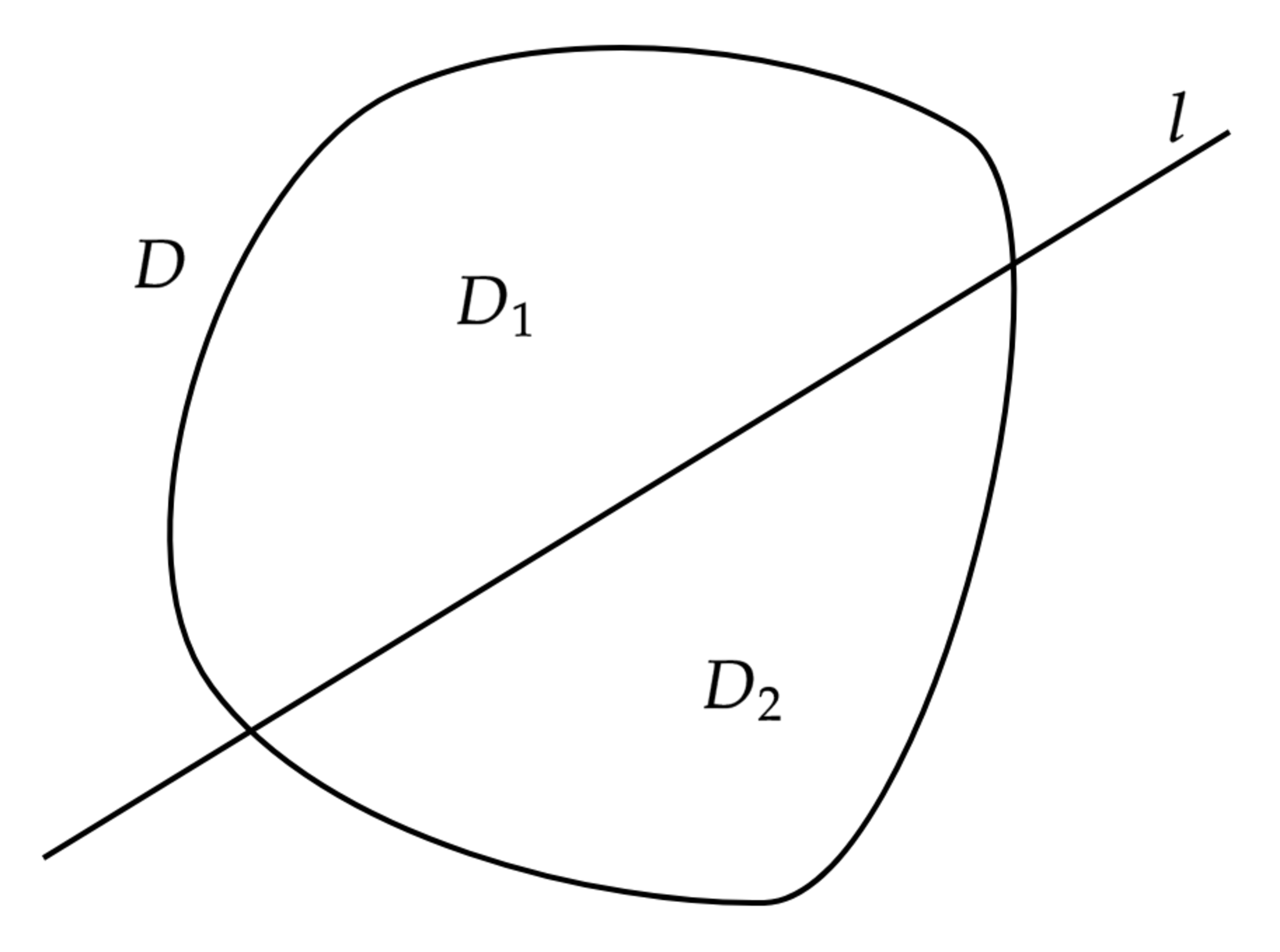
解答は こちら に書いていますのでよろしければご覧ください．なかなか面白い解法だと思います．後にパンケーキの定理を知って驚きました．本定理はその亜種にあたり，凸制約を課すことで一意性までを主張しています．
これがどのように$4$回対称へつながるか説明します．もし図形が$4$回対称性を持つならば，その回転中心で直交する$2$つの直線によって$4$つの合同な部分に分けられます．特に面積を持つときは$4$つの等積な部分に分けられるといえます．そこで，面積を$4$等分する$2$直線の交角の$\frac{\pi}{2}$への近さを所望の尺度として取り出せばよいのではないかと思いつきました．面積を$４$等分する$2$直線の組のうち一方が与えられればもう一方は一意に定まることを主張しているのが上記のパズルです．
擬$4$回対称性へ
前の話に加えて，面積を$2$等分する直線は傾きが与えられるとちょうど一つずつ存在しますから，$４$等分する$2$直線の組をこの傾きにより捕捉できます．ただし，それでも一般に面積を$４$等分する$2$直線の組というのは無数にありますし，交角の最大値について次のことが成り立ちます．
ユークリッド平面上に有界閉凸領域$D$がある．
このとき，$D$の面積を$4$等分する$2$直線$l,m$であって直交するものが存在する．
よって，擬$4$回対称を定式化するには交角の最小値が適した数値であると言えそうです．すなわち，ユークリッド平面上の有界閉凸領域$D$に対して，$D$の面積を$4$等分する$2$直線のなす(小なる方の)角の大きさの下限を$\varphi (D)\ (0 \leq \varphi (D) \leq \frac{\pi}{2})$とします(これは最小値にもなっています)．すると晴れて擬$4$回対称の定義が得られます．
$c\in (0,1] $とする．
平面上の有界閉なる凸図形$D$が$c$-擬$4$回対称であるとは，
$$\varphi (D)=\frac{\pi}{2}c$$
となることをいう．
ただちに次のことがわかります．
$D$は$4$回対称$ \Longrightarrow $$D$は$1$-擬$4$回対称
この逆は未解決のまま放置しています．
$D$は$1$-擬$4$回対称$ \Longrightarrow $$D$は$4$回対称
すなわち，$D$の面積を$4$等分するどんな$2$直線$l,m$も直交するならば，$D$は$4$回対称である．
例えば$4$回対称に最も近い三角形はなんでしょうか？あるいは平べったい二等辺三角形を考えれば$4$回対称性からいくらでも遠ざけることができます．色々と考えたいものが出てきますね．少しでもワクワクしていただけたら幸いです．