自作パズル『計13枚のコインと天秤パズル』
初投稿です.表現下手なところがあるので温かい目で見ていただけると幸いです.
はじめに
天秤パズルをもとにしたパズルを作りました!ぜひ,挑戦してみてください!
「そもそも天秤パズルとは?」という人向けに天秤パズルの紹介もしています.
「知ってる!」と言う人は,
自作パズルに挑戦
へ飛んでいただいても大丈夫です.
天秤パズルとは?
天秤パズル(balance puzzle, weighting puzzle)とは,天秤を限られた回数使って重さの違うコインを探し出す論理パズルです.さっそくですが,例題を見てみましょう.
あなたはコインを9枚持っています.そのうち1枚だけ重さが重いコインがあるそうです.天秤を2回使って重いコインを探し出してください.

この問題は,次で解くことができます.
説明のために,コインに1から9までの数字をつけておきます.
- コイン1,2,3を左に,コイン7,8,9を右に置き,重さを比べる.
左に傾く$\Rightarrow$1,2,3のどれかが重い.
傾かない$\Rightarrow$4,5,6のどれかが重い.
右に傾く$\Rightarrow$7,8,9のどれかが重い. - コイン1,4,7を左に,コイン3,6,9を右に置き,重さを比べる.
左に傾く$\Rightarrow$1,4,7のどれかが重い.
傾かない$\Rightarrow$2,5,8のどれかが重い.
右に傾く$\Rightarrow$3,6,9のどれかが重い. - 1.,2.で共通して重いと予想されたコインが答え.

図のように,天秤の左右にコインを置くと左右に傾いたり,傾かなかったりします.その結果を使って重さの違うコインを当てるパズルが天秤パズルです.なんとなくわかっていただけたでしょうか?
どんなパズルかわかっていただけたところで,もう一つ例題を出します.
あなたはコインを4枚持っています.そのうち1枚だけ重さが違う(重い or 軽い)コインがあるそうです.天秤を2回使ってそのコインを探し出してください.

この問題のように,重いか軽いかがわからないタイプの問題もあります.
この問題は,次で解くことができます.
説明のために,コインに1から4までの数字をつけておきます.
- コイン1を左に,コイン2を右に置き,重さを比べる.
左に傾く$\Rightarrow$1が重いか,2が軽い.
傾かない$\Rightarrow$3,4どっちかの重さが違う(重い or 軽い).
右に傾く$\Rightarrow$1が軽いか,2が重い. - コイン1を左に,コイン3を右に置き,重さを比べる.
左に傾く$\Rightarrow$1が重いか,3が軽い.
傾かない$\Rightarrow$2,4どっちかの重さが違う(重い or 軽い).
右に傾く$\Rightarrow$1が軽いか,3が重い. - 1.,2.で共通して出てきたものが答え.
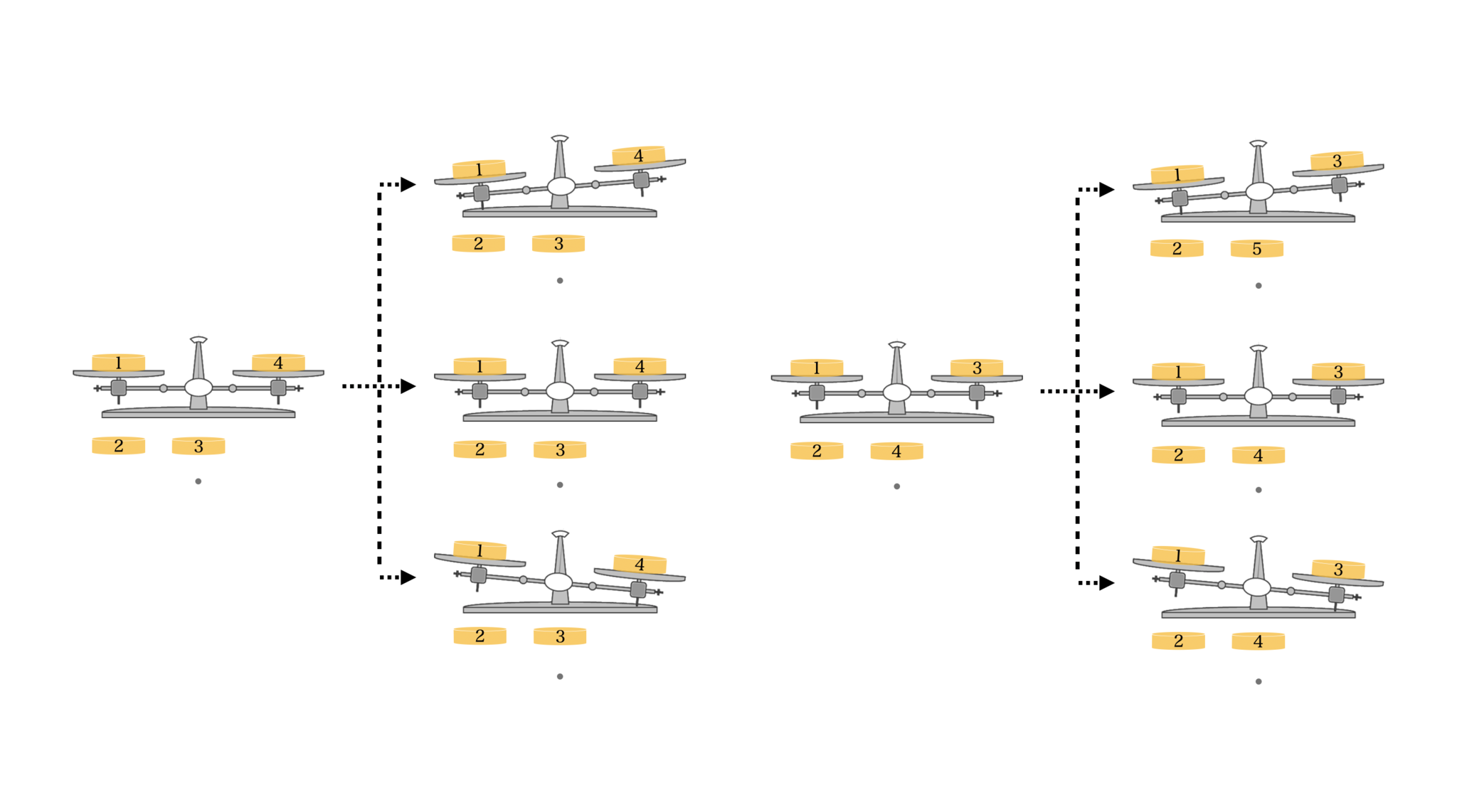
重いか軽いかがわからないと難しくなりますね….
もっとコインの枚数が多くなったらどうですか?解けそうですか?2つ問題を出しておくので,ぜひ挑戦してみてください!
あなたはコインを27枚持っています.そのうち1枚だけ重さが重いコインがあるそうです.天秤を3回使って重いコインを探し出してください.

あなたはコインを13枚持っています.そのうち1枚だけ重さが違う(重い or 軽い)コインがあるそうです.天秤を3回使ってそのコインを探し出してください.

天秤パズルの解法
この章では,天秤パズルの解法を紹介します.
天秤パズルの定式化
解法を考える前にパズルを深掘りしておきたいと思います.
前章で紹介したように,天秤パズルはタイプが2つあり,次の形をしていました.
例題1のタイプ:
あなたはコインを$c$枚持っています.そのうち1枚だけ重さが重いコインがあるそうです.天秤を$n$回使って重いコインを探し出してください.
例題2のタイプ:
あなたはコインを$c$枚持っています.そのうち1枚だけ重さが違う(重い or 軽い)コインがあるそうです.天秤を$n$回使ってそのコインを探し出してください.
今回は説明の都合上扱いませんが,実は次のような天秤パズルもあります.
あなたはコインを12枚持っています.それらコインは重さが全て同じか,1枚だけ重さが違う(重い or 軽い)そうです.天秤を3回使って重さが違うコインがあるかを判定し,重さが違うコインがある場合はそのコインを見つけてください.
このタイプの問題に関しては,また後日記事を書きたいと思います.
これから,この2つのタイプの問題を深掘りしていきます.説明の都合上,コインには1から$c$までの数字がついていることとします.
条件の定式化
まずは,条件にあたる次の部分の定式化を考えていきましょう.
- そのうち1枚だけ重さが重いコインがあるそうです
- そのうち1枚だけ重さが違う(重い or 軽い)コインがあるそうです
これらは,数字$i$がついたコインの重さを$w_i$とすると,次で定式化できます.
$\exists w \in \mathbb{R}_{>0}, \exists w' \in \mathbb{R}_{>0}, \exists! \, i \in \{1, \ldots, c\}, \, \mathrm{s.t.} \,((\forall \, j \in \{1, \ldots, c\} \setminus\{i\}, w_j = w) \land (w_i = w+w'))$
$\exists w \in \mathbb{R}_{>0}, \exists w' \in \mathbb{R}_{\ne0}, \exists! \, i \in \{1, \ldots, c\}, \, \mathrm{s.t.} \,((\forall \, j \in \{1, \ldots, c\} \setminus\{i\}, w_j = w) \land (w_i = w+w'))$
この2つは,"$i$以外は同じ重さ$w$で,$i$は重さが$w'$違って$w+w'$.そんな$i$はひとつだけ"ということを表しています.$\exists$の部分に関しては,回答者には教えないけど…という感じでしょうか.
少しづつ形が違うのは,
- 例題1のタイプ:1枚だけ重さが重いので,差$w'$は正.
- 例題2のタイプ:1枚だけ重さが違う(重いor軽い)ので,差$w'$は0以外の数.
というところからきています.
天秤の定式化
次は,天秤の操作にあたる部分の定式化を考えていきましょう.
考える土台がないと難しいので,
例題1の解法
をもとに定式化を考えていきます.
天秤を使ったのは,次の操作でした.
コイン1,2,3を左に,コイン7,8,9を右に置き,重さを比べる.
これは,
- $w_1+w_2+w_3 > w_7 + w_8 + w_9$
- $w_1+w_2+w_3 = w_7 + w_8 + w_9$
- $w_1+w_2+w_3 < w_7 + w_8 + w_9$
のいずれかが成り立つかを調べたことになります. これを言い換えると,
- $w_1+w_2+w_3 - w_7 - w_8 - w_9 > 0$
- $w_1+w_2+w_3 - w_7 - w_8 - w_9 = 0$
- $w_1+w_2+w_3 - w_7 - w_8 - w_9 < 0$
のいずれかが成り立つかを調べたことになります.さらに言い換えると,$\mathrm{sgn}(w_1+w_2+w_3 - w_4 +w_5 + w_6)$を得たことになります.
ただし,$\mathrm{sgn}$は実数の符号を返す関数で,実数$x \in \mathbb{R}$に対し,$\mathrm{sgn}(x) =
\begin{cases}
1 & x > 0 \\
0 & x = 0 \\
-1 & x < 0 \\
\end{cases}$としておきます.
$\mathrm{sgn}$を作用させた後の結果は,
- $1$のとき, 天秤が左に傾く
- $0$のとき, 天秤が傾かない
- $-1$のとき, 天秤が右に傾く
で,天秤の傾き方と対応します.
これで,一回の天秤の操作は定式化できました.
そういえば,例題1ではもう一回天秤を使っていましたね.
コイン1,4,7を左に,コイン3,6,9を右に置き,重さを比べる.
これは先ほど同様に考えると,$\mathrm{sgn}(w_1+w_4+w_7 - w_3 +w_6 + w_9)$を得たことになります.
この2つをまとめてものが次になります.
$\mathrm{sgn}\left(\left(\begin{array}{cccccccccc}
1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & -1 \\
1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1
\end{array}\right)
\left(\begin{array}{c}
w_1 \\
w_2 \\
w_3 \\
w_4 \\
w_5 \\
w_6 \\
w_7 \\
w_8 \\
w_9
\end{array}\right)\right)$を得ること.
ただし,実数$x_1, \ldots, x_n \in \mathbb{R}$に対し,$\mathrm{sgn}\left( \left(\begin{array}{c}
x_1 \\
\vdots \\
x_n
\end{array}\right)\right) =
\left(\begin{array}{c}
\mathrm{sgn}(x_1) \\
\vdots \\
\mathrm{sgn}(x_n)
\end{array}\right)$とします.
行列で書いてあげることで,2つの式を1つにまとめることができました.
これをもとにすると,天秤を$n$回使うは次で表せます.
$b_{1,1}, \ldots, b_{1,c}, \ldots, b_{n,1}, \ldots, b_{n,c}, \in \{1, 0, -1\}$に対し,$\mathrm{sgn}\left(\left(\begin{array}{ccc} b_{1,1} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_c \end{array}\right)\right)$を得ること.
ここで現れる$b_{i,j} \in \{1, 0, -1\}$は,
- $b_i = 1$のとき, コイン$i$を天秤の左にのせる
- $b_i = 0$のとき, コイン$i$を天秤にのせない
- $b_i = -1$のとき, コイン$i$を天秤の右にのせる
で,天秤へのコインの乗せ方と対応します.例題1のコインの置き方と行列の関係を確認してみてください.
天秤パズルの解法
条件,天秤の操作の定式化ができたので,解法を考えていきましょう.
一般的な解法
条件の定式化より,$i$を重さの違うコインとしたとき,$w_i$以外の重さは$w$,$w_i$の重さは$w+w'$で書けることをふまえると,天秤を$n$回使った結果は次になります.
$\mathrm{sgn}\left(\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w+w' \\ \vdots \\ w \end{array}\right)\right)\begin{array}{c} \\ \\ \leftarrow i \, \text{行目} \\ \\ \\ \end{array}$
抽象的でわかりづらいですね….具体例を一つあげておきます.
例題と同じ天秤の置き方をして,数字3のついたコインが重かったとします(仮に,他のコインの重さが100.数字3のついたコインの重さがそれより50重かったとします).このとき,天秤を2回使った結果は,
$\mathrm{sgn}\left(\left(\begin{array}{cccccccccc} 1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & -1 \\ 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 \end{array}\right) \left(\begin{array}{c} 100 \\ 100 \\ 100+50 \\ 100 \\ 100 \\ 100 \\ 100 \\ 100 \\ 100 \end{array}\right)\right)= \mathrm{sgn}\left(\begin{array}{c} 50 \\ -50 \end{array}\right) =\left(\begin{array}{c} 1 \\ -1 \end{array}\right)$
となります.ちなみに,結果の解釈の仕方は,$1$が左に傾くで,$-1$が右に傾くだったので,この結果から1回目は左,2回目は右に傾いたことが分かります.
天秤を$n$回使った結果がわかったところで,結果から重さの違うコイン(すなわち,$i$)の見つけ方を考えていきましょう.そのために,結果をもう少し詳しくみていきます.天秤を$n$回使った結果
$\mathrm{sgn}\left(\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w+w' \\ \vdots \\ w \end{array}\right)\right)$
は,行列の線形性より,
$\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w+w' \\ \vdots \\ w \end{array}\right)= \left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w \\ \vdots \\ w \end{array}\right)+ \left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} 0 \\ \vdots \\ w' \\ \vdots \\ 0 \end{array}\right)= \left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w \\ \vdots \\ w \end{array}\right)+ w' \left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)$
が成り立つことに注意すると,
$\mathrm{sgn}\left(\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w \\ \vdots \\ w \end{array}\right)+ w' \left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)\right)$
が成り立ちます.もしここで,
$\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w \\ \vdots \\ w \end{array}\right)=\left(\begin{array}{c} 0 \\ \vdots \\ 0 \\ \vdots \\ 0 \end{array}\right)$
とすることができたら,結果は
$\mathrm{sgn}\left(w' \left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)\right)= \mathrm{sgn}(w')\mathrm{sgn}\left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)= \mathrm{sgn}(w')\left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)$
となります.つまり,結果はコイン$i$の置き方と,差$w'$の正負のみで決まることになるのです.ちなみに,最初の等式は,実数$x,y \in \mathbb{R}$に対し,$\mathrm{sgn}(xy)=\mathrm{sgn}(x) \mathrm{sgn}(y)$より,次の等式は,自然数$i,j$に対し,$b_{i,j} \in \{1,0,-1\}$より成り立ちます.
ここまでわかってしまえば,後は簡単です.
問題1のタイプは,差$w'$が正なので,コイン$i$が重いときはコイン$i$の置き方(すなわち,$\left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)$)が結果に出てきます.そのため,結果と一致する置き方をしているコインを探すことで重いコインを見つけることができます.その際,重さが重いコインの候補が複数あっては困るので,同じ置き方をしているコインがないこと(すなわち,$i_1 \ne i_2$に対し,$\left(\begin{array}{c} b_{1,i_1} \\ \vdots \\ b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$)が必要となります.
問題2のタイプは,差$w'$が正か負なので,コインが$i$重いときはコインの置き方が,軽いときはコインの置き方と逆の結果が出てきます.そのため,結果と一致する置き方をしているコイン,または結果と置き方が左右逆のコインを探すことで重さの違うコインを見つけることができます.その際,重さの違うコインの候補が複数あっては困るので,同じ置き方をしているコインがないことと,左右逆の置き方をしているコインがないこと(すなわち,$i_1 \ne i_2$に対し,$\left(\begin{array}{c} -b_{1,i_1} \\ \vdots \\ -b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$)が必要となります.
コインの見つけ方はこれでいいのですが,これができるのは,
$\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,i} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{1,i} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w \\ \vdots \\ w \\ \vdots \\ w \end{array}\right)=\left(\begin{array}{c} 0 \\ \vdots \\ 0 \\ \vdots \\ 0 \end{array}\right)$
のおかげでしたね.この条件も考えてみると,左と右におくコインの数が同じこと(すなわち,$\# \{j \in \{1,\ldots,c\}\mid b_{k,j} = 1\} = \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = -1\}$)となります.「そんなの当たり前!」というような条件のおかげで,問題が簡単になるってすごくないですか!!
ここまでの議論をまとめておきます.
$b_{1,1}, \ldots, b_{1,c}, \ldots, b_{n,1}, \ldots, b_{n,c} \in \{1, 0, -1\}$が次の条件を満たすとする.
- $\forall k \in \{1,\ldots,n\}, \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = 1\} = \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = -1\}$
- $\forall i_1, i_2(\ne i_1) \in \{1,\ldots,c\}, \left(\begin{array}{c} b_{1,i_1} \\ \vdots \\ b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$
このとき,$\mathrm{sgn}\left(\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_c \end{array}\right)\right)= \left(\begin{array}{c} b_{1,i} \\ \vdots \\ b_{n,i} \end{array}\right)$なるコイン$i$が重さが重いコイン.
$b_{1,1}, \ldots, b_{1,c}, \ldots, b_{n,1}, \ldots, b_{n,c} \in \{1, 0, -1\}$が次の条件を満たすとする.
- $\forall k \in \{1,\ldots,c\}, \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = 1\} = \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = -1\}$
- $\forall i_1, i_2(\ne i_1) \in \{1,\ldots,c\}, \left(\begin{array}{c} b_{1,i_1} \\ \vdots \\ b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right) \land \left(\begin{array}{c} -b_{1,i_1} \\ \vdots \\ -b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$
このとき,$\mathrm{sgn}\left(\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_c \end{array}\right)\right)= \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$または,$\mathrm{sgn}\left(\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,c} \\ \vdots & \vdots & \vdots \\ b_{n,1} & \ldots & b_{n,c} \end{array}\right) \left(\begin{array}{c} w_1 \\ \vdots \\ w_c \end{array}\right)\right)= \left(\begin{array}{c} -b_{1,i} \\ \vdots \\ -b_{n,i} \end{array}\right)$なるコイン$i$が重さが違うコイン.
具体例
具体例として, 天秤パズルとは? で紹介した問題を解いてみたいと思います.
あなたはコインを27枚持っています.そのうち1枚が他のコインと比べ重いということがわかっています.天秤を3回使って重いコインを探し出してください.

これは,例題1と同じタイプなので,
- $\forall k \in \{1,\ldots,n\}, \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = 1\} = \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = -1\}$
- $\forall i_1, i_2 (\ne i_1) \in \{1,\ldots,c\}, \left(\begin{array}{c} b_{1,i_1} \\ \vdots \\ b_{n,i_1} \end{array}\right)\ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$
を満たすようなものを考えましょう.例えば,次が条件を満たします.
$\left(\begin{array}{ccccccccccccccccccccccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & -1 & -1 & -1 & -1 & -1 & -1 & -1 & -1 \\ 1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & -1 & 1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & -1 & 1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 & -1 \\ 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 & 1 & 0 & -1 \end{array}\right)$
この置き方を用いることで,前述の方法で重さの重いコインを見つけることができます.
あなたはコインを13枚持っています.そのうち1枚だけ重さが違う(重い or 軽い)コインがあるそうです.天秤を3回使ってそのコインを探し出してください.

これは,例題2と同じタイプなので,
- $\forall k \in \{1,\ldots,c\}, \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = 1\} = \# \{j \in \{1,\ldots,c\}\mid b_{k,j} = -1\}$
- $\forall i_1, i_2(\ne i_1) \in \{1,\ldots,c\}, \left(\begin{array}{c} b_{1,i_1} \\ \vdots \\ b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right) \land \left(\begin{array}{c} -b_{1,i_1} \\ \vdots \\ -b_{n,i_1} \end{array}\right) \ne \left(\begin{array}{c} b_{1,i_2} \\ \vdots \\ b_{n,i_2} \end{array}\right)$
を満たすようなものを考えましょう.例えば,次が条件を満たします.
$\left(\begin{array}{ccccccccc} 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 & -1 & -1 & -1 \\ 1 & 1 & 0 & -1 & 1 & 0 & 0 & -1 & -1 & 1 & 0 & 0 & -1 \\ 1 & -1 & -1 & 0 & 1 & 1 & 0 & 1 & 0 & -1 & 0 & -1 & 0 \\ \end{array}\right)$
この置き方を用いることで,前述の方法で重さの違うコインを見つけることができます.
自作パズルに挑戦
それではお待ちかねの自作パズルです.ぜひ挑戦してみてください!
あなたは金貨6枚,銀貨7枚の計13枚持っています.そのうち1枚だけ重さが違う(重い or 軽い)そうです.ここで重さが違うとは,同じ種類のコインと比べて重さが違うことを意味します(すなわち,金貨の中に1つだけ他の金貨と比べ重さが違うものがあるか,銀貨の中に1つだけ他の銀貨と比べ重さが違うものがあります).天秤を3回使って重さの違うコインを探し出してください.

金貨の重さと銀貨の重さが同じ場合は,天秤パズルと同じ問題ですが,今回は重さが同じかもしれないし,違うかもしれません.そんな条件でも解けるのでしょうか?
ヒント1
今まで議論が使えるかもしれません.飛んできた人は,これまでの内容を見てみましょう.
ヒント2
このパズルは,条件が変わっています.このパズルの条件を定式化するとどうなりますか?
ヒント3
このパズルの条件は次で定式化できます.
$\exists w_g, w_s \in \mathbb{R}_{>0}, \exists w' \in \mathbb{R}_{\ne0}, \exists! \, i \in \{1, \ldots, 13\}, \, \mathrm{s.t.} \,((\forall \, j \in \{1, \ldots, 6\} \setminus\{i\}, w_j = w_g ) \land (\forall \, j \in \{7, \ldots, 13\} \setminus\{i\}, w_j = w_s) \land (i \le 6 \Rightarrow w_i = w_g+w') \land (i \ge 7 \Rightarrow w_i = w_s+w'))$
複雑でわかりづらいかもしれませんが,基本的には天秤パズルのように重さの違うコイン以外は基本の重さ$w_g, w_s$で,重さの違うコインは$+w'$で表せるということです.
ヒント4
次に考えるのは解法です.解法のポイントはなんでしたか?
確か,『これがあると問題が簡単になる!!』っていう条件がありましたね.
ヒント5
『これがあると問題が簡単になる!!』という条件は,今回は次の条件です.
$\left(\begin{array}{ccccc} b_{1,1} & \ldots & b_{1,6} & b_{1,7} & \ldots & b_{1,13} \\ b_{2,1} & \ldots & b_{2,6} & b_{2,7} & \ldots & b_{2,13} \\ b_{3,1} & \ldots & b_{3,6} & b_{3,7} & \ldots & b_{3,13} \end{array}\right) \left(\begin{array}{c} w_g \\ \vdots \\ w_g \\ w_s \\ \vdots \\ w_s \end{array}\right)=\left(\begin{array}{c} 0 \\ \vdots \\ 0 \\ 0 \\ \vdots \\ 0 \end{array}\right)$
ヒント6
$\left(\begin{array}{ccccccccc} 1 & 1 & 0 & 0 & -1 & -1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 \\ 1 & -1 & 0 & -1 & 1 & 0 & 1 & 0 & 1 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & -1 & -1 & -1 & -1 & 1 & 0 & 1 & 0 & 0 \\ \end{array}\right) \left(\begin{array}{c} w_g \\ \vdots \\ w_g \\ w_s \\ \vdots \\ w_s \end{array}\right)=\left(\begin{array}{c} 0 \\ \vdots \\ 0 \\ 0 \\ \vdots \\ 0 \end{array}\right)$
が成り立ちます.
ヒント7
条件をふまえると,ヒント6のコインの置き方で天秤を3回使った結果はどうなりますか?
ヒント8
$\mathrm{sgn}\left(\left(\begin{array}{ccccccccc} 1 & 1 & 0 & 0 & -1 & -1 & 1 & 1 & 0 & 0 & 0 & -1 & -1 \\ 1 & -1 & 0 & -1 & 1 & 0 & 1 & 0 & 1 & 0 & -1 & 0 & -1 \\ 1 & 0 & 1 & 0 & -1 & -1 & -1 & -1 & 1 & 0 & 1 & 0 & 0 \\ \end{array}\right) \left(\begin{array}{c} w_g + w'\\ \vdots \\ w_g \\ w_s \\ \vdots \\ w_s \end{array}\right)\right)$
の結果はどうなりますか?
ヒント9
ヒント8の$w'$の位置を1行目から他の行に変えてみましょう.
重さの違うコインの見つけ方がわかるはずです!
おわりに
途中に出てきた,『これがあると問題が簡単になる!!』という条件は,符号理論という分野でとても大切な条件になっています.今回の自作パズルもそこからの発想です(伝わる人がいるかはわかりませんが,オール1(全部同じ値)以外の符号語を考えてみたらこのパズルができました).このパズルを通じて,少しでも興味を持っていただけたら嬉しいです.また,このパズルも気に入ってくれると嬉しいです.
