【Causality】時空が多様体上の時間バンドルとなるための十分条件
時空は局所的には(時間)×(多様体)と分解できますが、大域的にはどうでしょうか、という話です。この話題を数学的にしっかり定式化して論じていきます。この記事はSteven Harrisの論文「Conformally stationary spacetimes」を勉強したときのノートでもあります。なので読者想定としてある程度の微分幾何と相対論の教養は仮定します。議論歓迎します。何でもコメントどうぞ。
まず次の定理がこの問題に対する基本的な定式化であり、問題意識でもあり、出発点です。
時空$(M,g)$はchronologicalとし、$U$を完備な時間的ベクトル場とする。$U$の軌道空間を$Q$とすると、$M$は$U$の積分曲線をファイバーとする近多様体$Q$上のprincipal line bundleとなる。
登場した言葉の定義をしておきます。時空とは時間的向き付け可能なLorentz多様体のことです。chronologicalとは閉じた時間的曲線が存在しない時空のことです。$U$の軌道空間とは時空$M$に同一の$U$の積分曲線上にあるものを同一視する同値類を入れたときの商空間のことです。近多様体とは局所的にEuclid空間と同相な近傍が存在する可算基を持つ位相空間です。近多様体がHausdorffなら多様体(paracompact Hausdorff位相空間)となります([3], proposition 1.15.1)。
$U$の生成する1パラメータ変換群を$\phi_t$とする。$\mathbb{R}$の$M$への作用を$\phi_t$で定める。この作用が局所的に部分多様体で与えられるスライスを持つことを示せば十分である。
[2]のProposition2.2.2によれば、任意の点$p\in M$に対して、$p$の近傍$W$があって、十分大きい$|t|$に対して、$\phi_t(W)\cap W=\emptyset$となるならば滑らかな部分多様体のスライスを持つことが従う。
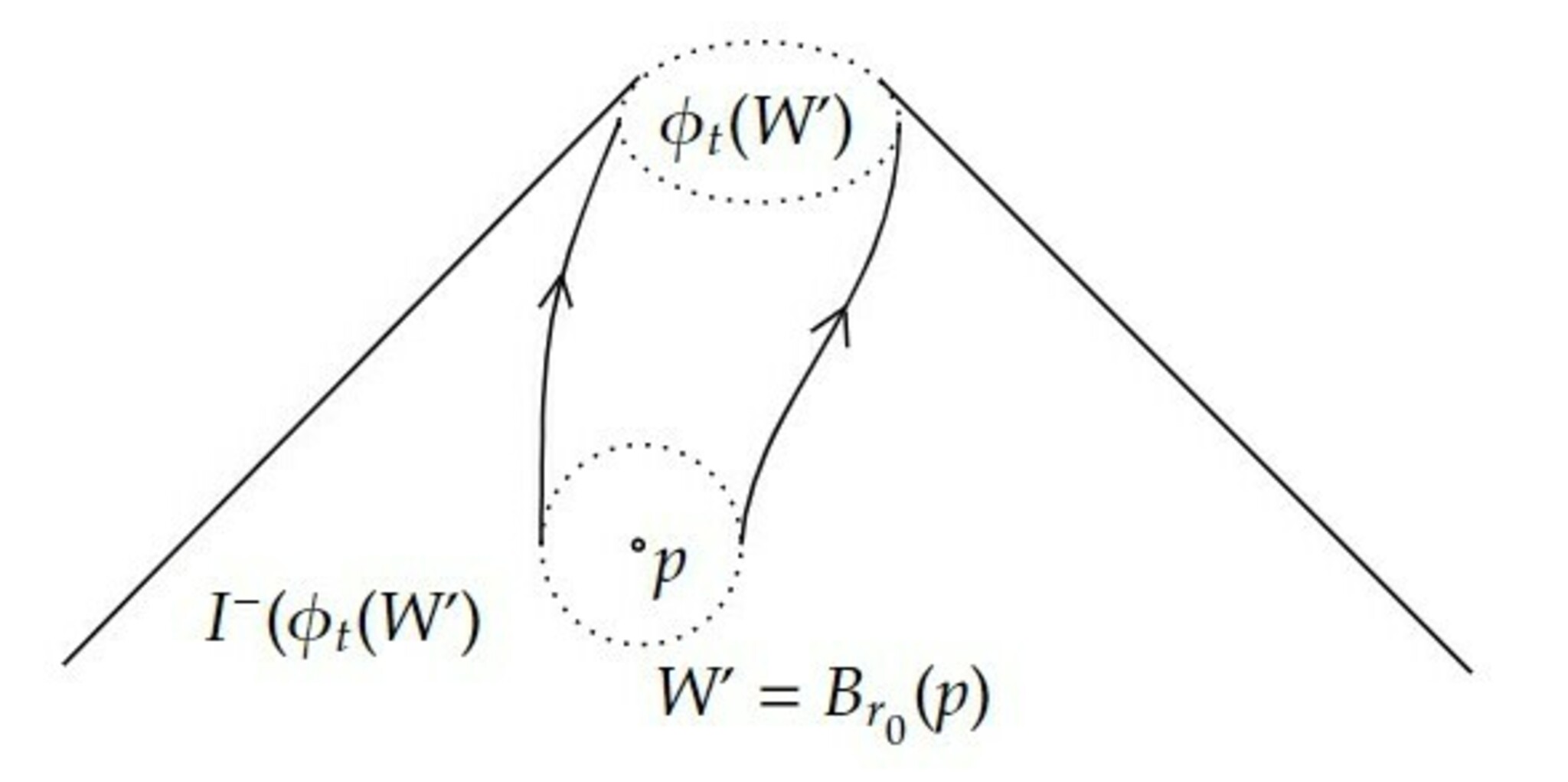
$U$は未来向きであるとして一般性を失わない。任意の点$p\in M$の小さい近傍を$V$とする。$M$に任意にリーマン計量$h$を入れ、$h$に関する半径$r$、中心$q$の測地球を$B_r(q)$と書くことにする。実数$t_0>0$を任意に選び固定する。$q\in V$に対して、$B_{R(q)}(q)\subset I^-(\phi_{t_0}(q))$を満たすように関数$R\in C^\infty(V)$を定める。$r':=\inf_{q\in V}R(q)$とし、$r_0=r'/2$とすると、任意の2点$q_1,q_2\in B_{r_0}(p)$に対して、$q_2\in B_{2r_0}(q_1)\subset I^-(\phi_{t_0}(q_1))$である。
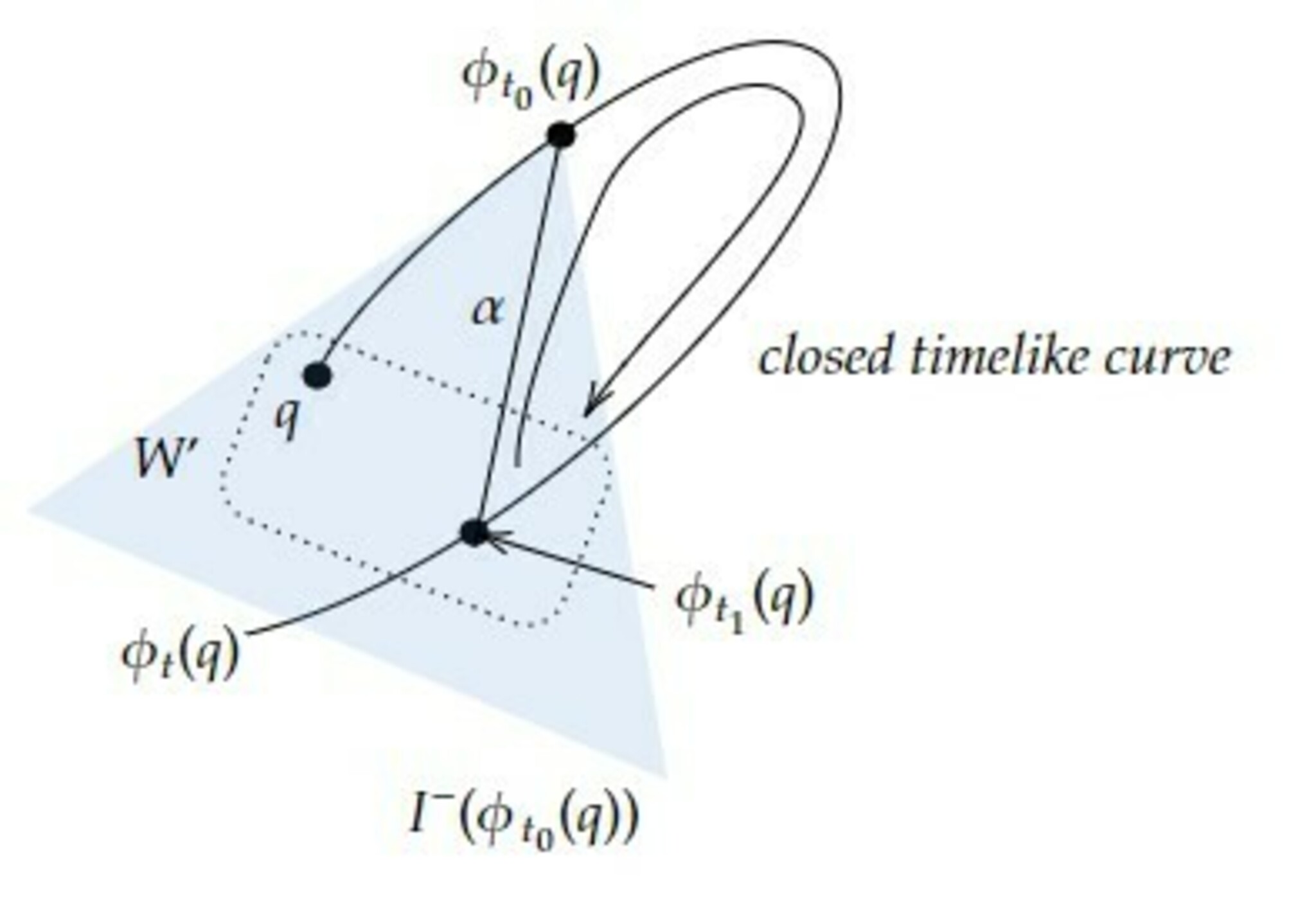
$q\in B_{r_0}(p)$と十分大きい$t>t_0$に対して、$\phi_t(q)$は$W'=B_{r_0}(p)$と交わらない。なぜなら、もし交わるとすれば、ある$t_1(>t_0)$に対して、$\phi_{t_1}(q)\in W'$となるが、$W'$の作り方から$I^-(\phi_{t_0}(q))\ni\phi_{t_1}(q)$となり、$\phi_{t_1}(q)$から$\phi_{t_0}(q)$への未来向きtimelike曲線が存在し、従って閉timelike曲線が存在することになり、chronologicalであることに矛盾するからである(図2参照)。
上の処方を$t<0$に対しても行って$p$の近傍$W''$で十分小さい$t<0$に対して、$\phi_t(W'')\cap W''=\emptyset$となるものが取れる。
$W=W'\cap W''$とすれば望みの近傍が得られる。
 証明の模式図1
証明の模式図1
 証明の模式図2
証明の模式図2
時空がchronologicalで$U$が完備という条件を課してもまだ一般には多様体上の時間バンドルとはならないという事実は動的な時空を考察するときには注意するべきことです。
chronologicalという条件を外すともはや近多様体にすらなりません。
2次元Minkowski時空$(\mathbb{R}^2,ds^2=-dt^2+dx^2)$を$(t,x)\sim(t+n,x+m),\ n,m\in\mathbb{Z}$と同一視してトーラスにすればchronologicalでなくなる。このとき
ベクトル場$U=\partial_t+\alpha\partial_x,\ (0<\alpha<1,\ \alpha\in\mathbb{R}\backslash\mathbb{Q})$は完備だが、積分曲線は時空全体で稠密となり、その商空間$Q$には密着位相が入る。
また定理1の設定で軌道空間が多様体でない近多様体となる例として以下のものがあります。
3次元Minkowski時空$Min^3$から1点$(0,0,0)$を取り除いた$N=Min^3-(0,0,0)$を考える。$N$上のベクトル場$U=\lambda(t,x,y)\partial_t,\ \lambda(t,x,y)\in C^\infty(N)$は時間的なベクトル場である。$\lambda$を適切な関数にすると$U$は完備なベクトル場になる。実際、正の滑らかな関数$\lambda$を以下の図1のように定める。
![関数!FORMULA[66][-430909185][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220101183839.jpg?alt=media) 関数$\lambda(x,y,t)$
関数$\lambda(x,y,t)$
$(x_0,y_0)\ne(0,0)$に対して、$\int_{t_0}^{\pm\infty}\lambda^{-1}(x_0,y_0,t)dt\rightarrow\pm\infty$である。また、$t_0<0$に対して、$\int_{t_0}^{0-}\lambda^{-1}(0,0,t)dt\rightarrow\infty$であり、$t_0>0$に対しても同様であるからベクトル場$U$は完備である。
このとき、$U$の軌道空間$Q$の点$0^+:=[(0,0,t)],\ (t>0)$と点$0^-:=[(0,0,t)],\ (t<0)$はそれぞれ互いを含む$\mathbb{R}^2$の近傍と同相な近傍を持つ。
さて、どのようなときに底空間、すなわち軌道空間が多様体となるでしょうか。その十分条件を与えるのが以下の定理2です。
timelike Killingベクトル場を持つ時空を定常時空という。またtimelikeな共形Killingベクトル場を持つ時空を共形的定常時空という。
当然、共形的定常時空は定常時空を含んでいます。また共形Killingベクトル場$U$に対してスカラー関数$\lambda$があり、$\mathcal{L}_Ug=\lambda g$となりますが、$\lambda$の符号が一定であるとき、$U$は単調であるということにします。
定常時空に関して少し補足しておきます。定常なら局所的に時空の計量は
$g=-(dt+\eta)^2+h$
と書かれます。ただし、$h$は局所的に任意に選ばれたspacelike hypersurface $N$上に誘導されたリーマン計量で、$\eta$は$N$上の1-form(を引き戻したもの)です。もちろんこれは局所的な表示でしかありません。時空全体で大域的に計量がこのように分解が可能かどうかは全く自明ではありません(分解するための十分条件については別のノートで扱います)。
定常時空が多様体上の(時間の)line bundleとなるための十分条件は以下です。
時空$(M,g)$はchronologicalかつ時間的で完備な単調共形Killingベクトル場$U$が存在するとする。このとき$U$の軌道空間$Q$は多様体(paracompact Hausdorff位相空間)であり、$M$は$Q$上のprincipal line bundleである。ただしそのファイバーは$U$の積分曲線である。
定理1より軌道空間$Q$がHausdorffであることを示せばよい。
$\mathcal{L}_Ug=\lambda g,\ \lambda>0$とし、$U$が生成する1パラメータ変換群を$\phi_t$とすると、$p\in M$に対して、$(\phi_t^\ast g)_p=L(p,t)g_p,\ L(p,t):=\exp\int_0^t\lambda(\phi_s(p))ds$である。なぜなら、任意の$X_p\in T_pM$を$[U,X]=0$となるように拡張すると、$\frac{d}{dt}||X(\phi_t(p))||^2=\lambda(\phi_t(p))||X(\phi_t(p))||^2$となるからである。また$t<0$なら$L(p,t)\le 1$である。
リーマン計量$h=g+\frac{2}{||U||^2}{}^\flat U\otimes{}^\flat U$に対して$\mathcal{L}_Uh=\lambda h$となることが簡単に確認できる。
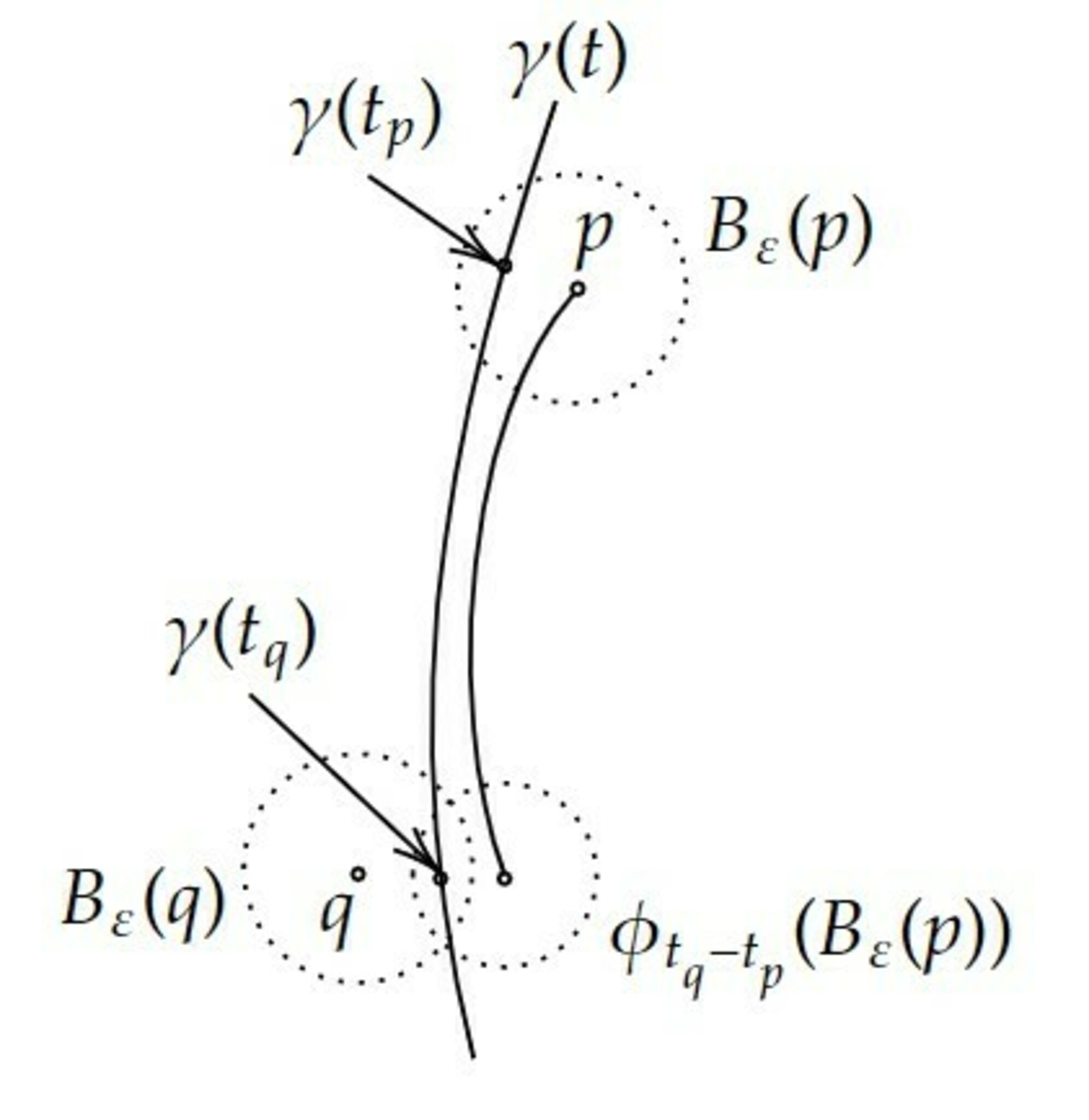
$\pi:M\rightarrow Q$とし、2点$p,q\in M$に対して、$\pi(p)$と$\pi(q)$の任意の近傍が共通部分を持つとする。すなわち任意の$\varepsilon$に対して、$U$のある軌道$\gamma(t)$があり、$\gamma(t_p)\in B_{\varepsilon}(p),\ \gamma(t_q)\in B_{\varepsilon}(q)$となる。このとき$t_p>t_q$としてよい。ただし、距離は$h$で図るものとする。
上の事実($t<0$なら$L(p,t)\le 1$)より、$||\gamma(t_q)-\phi_{t_q-t_p}(p)||_h<\varepsilon$であるから、$||q-\phi_{t_q-t_p}(p)||_h<2\varepsilon$である。
これは$p$を通る$U$の軌道が$q$の任意の近傍を通ることを示している。従って$\pi(p)$は$\pi(q)$の任意の近傍に含まれる。$Q$は局所ユークリッドな近傍を持つから$\pi(p)=\pi(q)$である。
 証明の模式図
証明の模式図
定理2の設定において、$M\simeq\mathbb{R}\times Q$であり、$g$と共形同値な計量$\bar{g}$で$U$がKillingベクトル場となるが存在する。
多様体上のprincipal line bundleには大域的な滑らかな切断が存在する([Kobayashi,Nomizu] Theorem I.5.7)ことから、$M\simeq\mathbb{R}\times Q$となる。この滑らかな切断を$Q$と同一視する。
$M$上の関数$\varphi\in C^\infty(M)$で$U\varphi=\lambda$を満たすものが存在する。実際、$M=\mathbb{R}\times Q$と$Q$上の初期条件から偏微分方程式$U\varphi=\lambda$は$M$全体で一意的に解を持つ。
$\bar{g}=e^{-\varphi}g$とすると、$\mathcal{L}_U\bar{g}=e^{-\varphi}(-U\varphi+\lambda)g=0$となり、$\bar{g}$に関して$U$はKillingベクトル場である。
これでchronologicalで単調な共形的定常時空であればある多様体$Q$上の時間バンドル(直積バンドル)として時空$\mathbb{R}\times Q$と表せることが分かりました。また系より共形的定常時空ではなく単に定常時空を考えれば十分であることも分かりました。しかしこの多様体$Q$を“空間”と解釈することはまだできません。というのも$Q$に微分同相な$M$の部分多様体で誘導計量が正定値となるものが存在するかどうかはまだ証明されていないからです。実は上の定理の設定では正定値となることは一般には成り立たないのです。このことに関してはまた別のノートでまとめることにします。
