相関係数と線形回帰の関係

概要

2次元データ$x_i,\; y_i,\;(i=1,\ldots,N)$があるとき，相関係数$r$が定義されます．
相関係数は線形な関係の強弱を測る指標である[※1]ので，ある程度$r$が$\pm1$に近ければ線形回帰でデータをよく説明できることが期待されます．
このとき，$r$と1次線形回帰の精度との間にはどのような関係があるのでしょうか．

結論としては，回帰直線からの平均二乗誤差$\rm RMSE_{\text{lin}}$と$r$の間に
$$\mathrm{RMSE}_{\text{lin}}=\sigma[y]\sqrt{1-r^2}$$
という関係があります．
例えば$r=0.8$のとき，$\mathrm{RMSE}_{\text{lin}}=0.6\sigma[y]$で，図示すると以下のようになります．

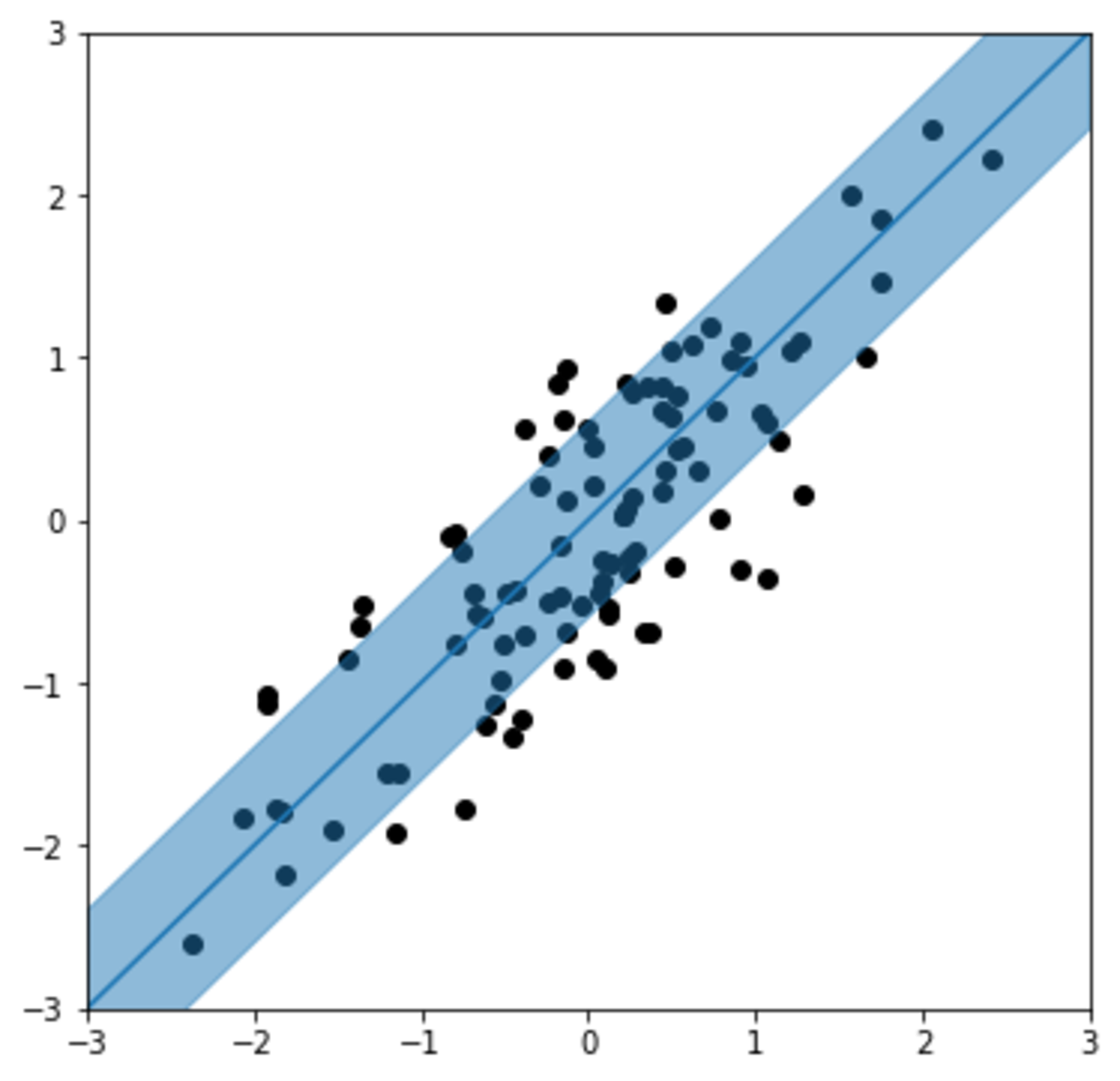相関係数 r=0.8 のデータにおける線形回帰と予測幅(±1SD)

個人的な感想としては，$r=0.8$というとそこそこ相関が強い印象があるので意外と範囲が大きいなと感じました．
ちなみに，ベースラインとして$y$のデータ点からランダムにサンプリングするモデルは$\mathrm{RMSE}_{\text{random}}=\sqrt{2}\sigma[y]$となるので，ここから考えると$58\%$の向上です．

証明

相関係数を$x,y$で表すと，

$$ r=\frac{\mathrm{Cov}[x,y]}{\sigma[x]\sigma[y]} =\frac{\mean{\paren{x-\mean x}\paren{y-\mean y}}}{\sqrt{\mean{\paren{x-\mean x} ^2}}\sqrt{\mean{\paren{y-\mean y}^2}}} =\frac{\mean{xy}-\mean x\mean y}{\sqrt{\paren{\mean{x^2}-\mean{x}^2}\paren{\mean{y^2}-\mean{y}^2}}} $$

（$\mean \bullet$はデータに対する平均$\frac1N\sum_{i=1}^N\bullet_i$を表す）
特に，$\mathrm{Var}[X]=\mean{\paren{X-\mean{X}}^2}=\mean{X^2}-\mean{X}^2$，$\mathrm{Cov}[X,Y]=\mean{\paren{X-\mean X}\paren{Y-\mean Y}}=\mean{XY}-\mean X\mean Y$は有名な公式ですが，式変形中によく使うので下で導出を示します．

一方，線形回帰$y=ax+b$を考えると，以前の記事 傾きを共有して切片が異なるデータ列の線形回帰 に示したように，係数は
$$ a=\frac{\mean{xy}-\mean{x}\mean{y}}{\mean{x^2}-\mean{x}^2},\;b=\mean{y}-a\mean{x} $$
となります．
$$ \mathrm{RMSE}=\sqrt{\frac1N\sum_{i=1}^N \paren{y^{\text{pred}}_i-y_i}^2} =\sqrt{\mean{\paren{y^{\text{pred}}-y}^2}} $$
で，線形回帰では$y^{\text{pred}}=ax+b$なので，第2項の分子について，
$$ {\mathrm{RMSE}_{\text{lin}}}^2=\mean{\paren{y^{\text{pred}}-y}^2} =\mean{\paren{ax+b-y}^2}\\ =\mean{\paren{ax+\mean y-a\mean x -y}^2} =\mean{\paren{a\paren{x-\mean x} -\paren{y-\mean y}}^2}\\ =\mean{a^2\paren{x-\mean x}^2 - 2a\paren{x-\mean x}\paren{y-\mean y} +\paren{y-\mean y}^2}\\ =a^2\mathrm{Var}[x]-2a\mathrm{Cov}[x,y]+\mathrm{Var}[y]\\ =\paren{\frac{\mean{xy}-\mean{x}\mean{y}}{\mean{x^2}-\mean{x}^2}}^2\paren{\mean{x^2}-\mean{x}^2} -2\frac{\mean{xy}-\mean{x}\mean{y}}{\mean{x^2}-\mean{x}^2}\paren{\mean{xy}-\mean{x}\mean{y}}+\mean{y^2}-\mean{y}^2\\ =\mean{y^2}-\mean{y}^2-\frac{\paren{\mean{xy}-\mean{x}\mean{y}}^2}{\mean{x^2}-\mean{x}^2}\\ =\mathrm{Var}[y]\paren{1-\frac{\paren{\mean{xy}-\mean{x}\mean{y}}^2}{\paren{\mean{x^2}-\mean{x}^2}\paren{\mean{y^2}-\mean{y}^2}}}=\mathrm{Var}[y](1-r^2) $$
$$ \therefore\quad \mathrm{RMSE}_{\text{lin}}=\sigma[y]\sqrt{1-r^2} $$

分散・共分散の変換

$$ \mathrm{Var}[X]=\frac1N\sum_{i=1}^N \paren{X_i-\mean{X}}^2\\ =\frac1N\sum_{i=1}^N \paren{X_i^2-2\mean{X}X_i+\mean{X}^2}\\ =\frac1N\sum_{i=1}^N X_i^2-2\mean{X}\frac1N\sum_{i=1}^NX_i+\mean{X}^2\frac1N\sum_{i=1}^N1\\ =\mean{X^2}-2\mean{X}^2+\mean{X}^2=\mean{X^2}-\mean{X}^2 $$

$$ \mathrm{Cov}[X,Y]=\frac1N\sum_{i=1}^N \paren{X_i-\mean X}\paren{Y_i-\mean Y}\\ =\frac1N\sum_{i=1}^N \paren{X_iY_i-X_i\mean Y-\mean XY_i+\mean X\mean Y}\\ =\frac1N\sum_{i=1}^N X_iY_i-\mean Y\frac1N\sum_{i=1}^N X_i-\mean X\frac1N\sum_{i=1}^N Y_i+\mean X\mean Y\frac1N\sum_{i=1}^N 1\\ =\mean{XY}-\mean{X}\mean{Y}-\mean{X}\mean{Y}+\mean{X}\mean{Y} =\mean{XY}-\mean X\mean Y $$

おまけ

$y$の分布に従って（つまり平均，分散が$y$のものと一致する），新たなデータ$y'_i\;(i=1,\ldots,N)$をサンプリングすると，$y'$は$x,y$の相関を考慮せず$y$の範囲だけを考えたランダムなモデルの予測値とみなせます．
このようなモデルをベースラインとすべく$\rm RMSE$を計算してみます．

$$ {\mathrm{RMSE}_{\text{random}}}^2=\mean{\paren{y'-y}^2}\\ =\mean{\paren{\paren{y'-\mean{y}}-\paren{y-\mean{y}}}^2}\\ =\mean{\paren{y'-\mean{y}}^2-2\paren{y'-\mean{y}}\paren{y-\mean{y}}+\paren{y'-\mean{y}}^2}\\ =\mathrm{Var}[y']-2\mathrm{Cov}[y',y]+\mathrm{Var}[y]\;(y'\text{の平均値は}y\text{のものと等しい})\\ =\mathrm{Var}[y']+\mathrm{Var}[y']\;(y'\text{と}y\text{は独立}\;\therefore\;\mathrm{Cov}[y',y]=0)\\ =2\mathrm{Var}[y]\;(y'\text{の分散は}y\text{のものと等しい}) $$
$$ \therefore\quad \mathrm{RMSE}_{\text{random}}=\sqrt{2}\sigma[y] $$

[※1]: 相関係数 - Wikipedia より

※本記事は，Quoraでの質問 相関係数が0.8とわかっている関係を使って相関係数1とみなした変換を行った場合、真の値とのズレはどのくらいになるでしょうか。最大20%？平均20%？それとも別の値になるでしょうか？ をもとに改稿したものです．