スピンは創発する？ファインマンが目指したこと

スピンとは何か

電子はスピンを持っていると言いますが、スピンとはなんでしょうか。

磁場をかけてそこに電子を飛ばすと、磁場をかけた軸に対し上に動くものと下に動くものがあります。そしてその先にスクリーンをおいておくと、電子の行き着く先は連続的に分布するのではなく、２点に絞られます。これがいわゆるシュテルン・ゲルラッハの実験（ホントの実験では銀原子を飛ばしている。Ref.[1]参照）です。この実験事実は、電子が2値をとる何らかの自由度を持っていることを示唆しています。これをスピンと呼びます。

シュテルン・ゲルラッハの実験。線源からスピンをもつ粒子を飛ばし、途中で磁場を縦方向にかけると、スクリーンの2点に粒子が辿り着く。元の実験では銀原子を飛ばしている

量子力学の教科書を見ると、角運動量演算子の半整数表現としてスピンが導入されます。初心者にはなんだかよくわからない導入なのですが、あまり難しいことは考えず、なんか離散的な2値をとる自由度がある、と割り切ることも大切です。

さて、なぜスピンは存在するのでしょうか。そんなことに答えがあるのかと思われるかもしれませんが、実はスピンは量子力学を相対論的に拡張しようとすると必然的に現れることが知られています。

量子論の基礎方程式であるシュレーディンガー方程式(ScE)は、相対論の要請であるローレンツ変換(LT)の下での不変性を満たしません。原因はScEが時間に関して1階微分なことです。ですのでシュレーディンガー方程式をLTの下で不変にするには、時間1階微分を2階微分にしてやればいいように見えます。しかしナイーブにこれを行うと、波動関数を確率として解釈できなくなります。これを完全に解決しようとすると場の量子論というものに移行しなくてはなりません。しかし、フェルミオンという粒子に限れば、「"4成分のScEライクな方程式"="Dirac方程式"」
$$ i\frac{\partial}{\partial t}\psi=-i\vec\alpha\cdot\nabla\psi+\beta m\psi,\\ \{\alpha_i,\alpha_j\}=0 \ \ \ i\neq j,\\ \{\alpha_i,\beta\}=0,\\ (\alpha_i)^2=\beta^2={\bf 1} $$
共変的に書けば
$$ i\gamma^\mu\partial_\mu\psi(x)-m\psi(x)=0,\\ \{\gamma_\mu,\gamma_\nu\}=2\eta_{\mu\nu},\\ \eta_{\mu\nu}:={\rm diag}(1,-1,-1,-1) $$

により、非相対論的量子力学と同様、波動関数の確率解釈を保った方程式を作ることができます。このとき波動関数$\psi$は4成分になるのですが、これはスピンの2自由度と粒子・反粒子の2自由度からなっています。すなわち、ScEを相対論的に拡張することにより、スピンと反粒子が現れます。

量子場の理論からスピンを語ると以下のようになります。量子場の理論はLTに対して不変でなくてはなりません。そこで、ローレンツ群の表現を調べ、それらからできる、LTに対して不変な組のみが理論に登場します。このとき表現としてスピノル表現が可能です。スピン1/2表現に対応する粒子の1つが電子です。

スピンを運動の法則から導く

20世紀物理学の巨匠R.P.Feynmanは、スピンの起源について面白い考察をしました。これは、Feynmanの業績のひとつである経路積分と関係します。経路積分は量子力学の定式化のひとつで、みんな最初に学ぶであろう正準量子化とは別の重要な量子化の方法です。特にゲージ場の量子論、またその数値計算においては欠くことができない手法となっています。

Feynmanは粒子の運動の結果としてスピンが現れるような可能性を考えました。FeynmanとHibbsの教科書"量子力学と経路積分"の問題2-6（Ref.[2]）に、その痕跡を見ることができます。以下時間1次元、空間1次元の場合を考えます。経路積分は、粒子の軌道全体$x(t)$で定まるある重み$\phi(x(t),\dot x(t),t)$があり、ある粒子が$a: (t_a,x_a)$から$b: (t_b,x_b)$に到達する確率振幅$K(b,a)$が
\begin{align} K(b,a)=\sum_{\text{全ての可能な$x(t)$の経路}}\phi(x(t),\dot x(t),t) \end{align}
と表わせるという原理に基づきます。確率振幅なるものがよくわからないかもしれませんが、その絶対値の2乗$|K(b,a)|^2$が$a$から$b$まで粒子が到達する確率となる量です。$\sum_aK(b,a)$という量を作ると、これは至るところから（＝場所を問わず）$b$に粒子が到達する確率振幅であり、波動関数$\psi(b)$だと解釈できます。
通常この$\phi(x(t),\dot x(t),t)$は、古典力学に現れる作用(action)と呼ばれる量$S(x(t),\dot x(t),t)$を用いて
\begin{align} \phi(x(t),\dot x(t),t)=\exp(iS(x(t),\dot x(t),t)/\hbar) \end{align}
と表わせます。

さて、Feynmanは、自由粒子が常に光速$c$で運動し、ただしその方向を時刻ごとに前後に変えるとしたとき、
\begin{align} \phi(x(t),\dot x(t),t)=(i\epsilon m)^R \ \ \ \tag{1} \end{align}
とすることで、相対論的な自由粒子の運動が導けることを見出しました（対応する作用は存在しませんが気にしないでください）。ここで$\epsilon$は運動の始まりの時刻$t_a$と終わりの時刻$t_b$を$N$等分したもので、
\begin{align} \epsilon=(t_b-t_a)/N \end{align}
です。粒子は$t=t_a+n\epsilon (n=1,2,\cdots,N-1)$の各時刻でその運動の方向の前後を任意に変えるとします。そして$R$は、$t_a$から$t_b$までの運動中に方向を変えた回数です（=軌道の角の数）。ただし、光速$c$と$\hbar$は1として（=これを基準として測ることで）消しています。$m$は粒子の質量です。

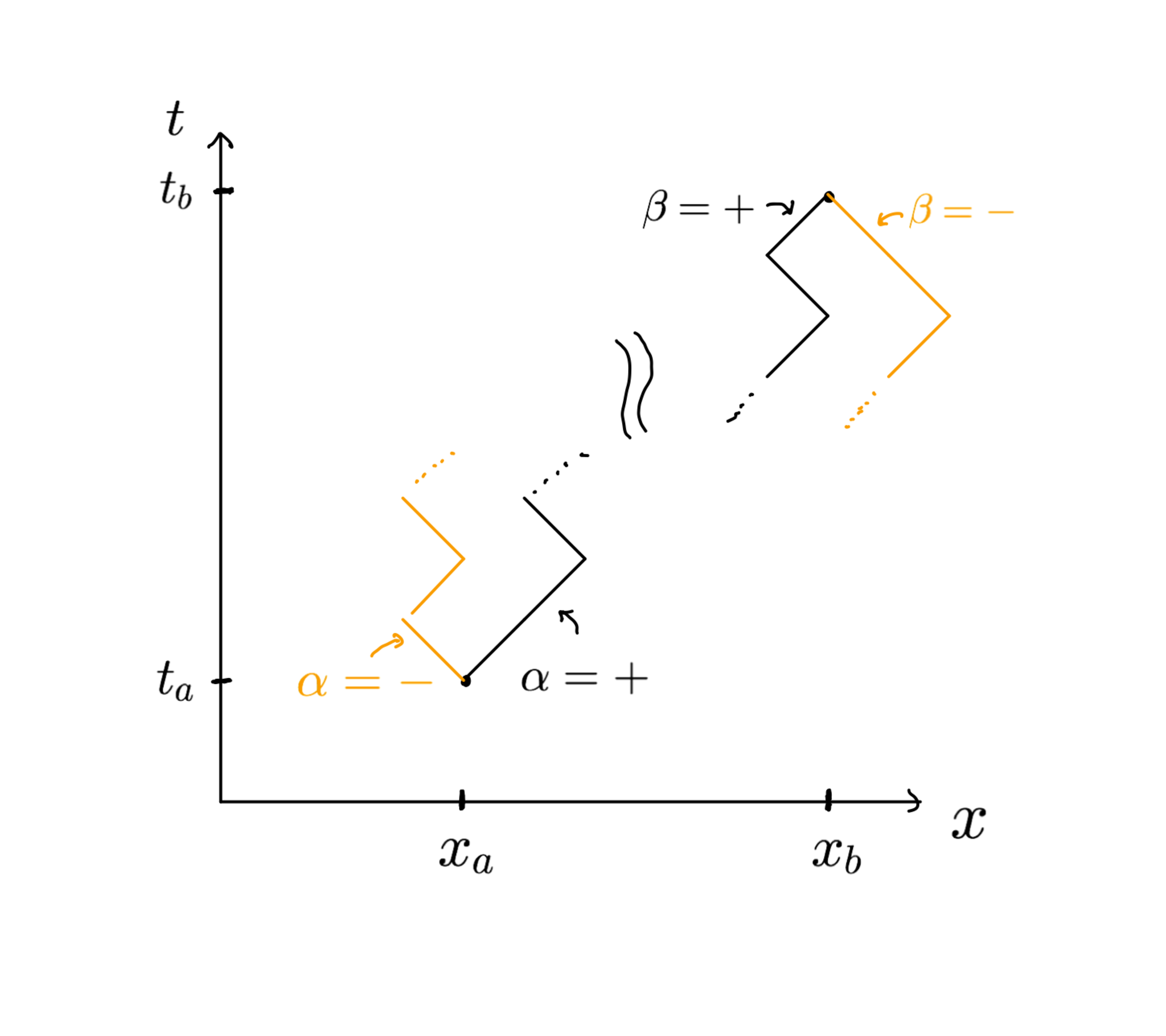粒子のたどる経路

これが相対論的な自由粒子の運動を表しているとはどういうことでしょう。それは、Eq.(1)から1+1d（時間1次元、空間1次元という意味）のDirac方程式
\begin{align} &(i\gamma^0\partial_0+i\gamma^1\partial_1)\psi-m\psi=0,\\ & \gamma^0= \begin{pmatrix} 0 & -1\\ -1 & 0 \end{pmatrix} , \ \gamma^1 = \begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix} \tag{2} \end{align}
を導けるからです。このとき、$\psi$は2成分です。

注目すべきは、Eq.(1)のどこにも2成分など出てきていないのに、Eq.(2)には2成分の$\psi$が現れているところです。これから見るとおり、粒子の運動の仕方の違いが、この2成分をもたらすことになります。

ただし先に書いておくと、この2成分はスピンには対応しません。4次元への拡張をすればスピン自由度が生まれるかというと、それも実は完全にはうまくいきません。ということで、このような試みは今ではあまり顧みられないのですが、アイディアとしてはなかなかおもしろいので、ここでちょっと紹介しておこうかと思います。

相対論的量子力学を導く

以下、Ref.[3]を元に議論します。

上記の確率振幅を以下のように書き換えましょう：
\begin{align} K_{\beta\alpha}(b,a)=\lim_{N\rightarrow\infty} \sum_{R\ge 0}\Phi_{\beta\alpha}(R)(i\epsilon m)^R \end{align}
これは曲がる回数$R$および$\alpha,\beta$で経路を場合わけし、その重み(=場合の数)を$\Phi_{\beta\alpha}(R)$として、
$R$で和をとることで確率振幅を求める形に書き直したものです。

以下$\Phi_{\beta\alpha}(R)$を求めます。

$K_{-+}$の計算

$R$回曲がるpathの$K_{-+}$への寄与を考えます。
このとき、左に$1+(R-1)/2$回、右に$(R-1)/2$回曲がります($R$:odd)。
ここで

• $P$: number of steps to right ($:=n_+$)
• $Q$: number of steps to left ($:=n_-$)

とします ($P+Q=N$)。このとき
\begin{align} \Phi_{-+}(R)&= \begin{pmatrix} P-1\\ \frac{1}{2}(R-1) \end{pmatrix} \begin{pmatrix} Q-1\\ \frac{1}{2}(R-1) \end{pmatrix} \\ &=\frac{(P-1)!}{\lr{\frac{1}{2}\lr{R-1}}!\lr{P-1-\frac{1}{2}\lr{R-1}}!} \cdot \frac{(Q-1)!}{\lr{\frac{1}{2}\lr{Q-1}}!\lr{Q-1-\frac{1}{2}\lr{Q-1}}!} \end{align}
となります。

$M=P-Q$とすると、$P=(N+M)/2, Q=(N-M)/2, P+Q=N, Q=N-P$です。
ここで$N\rightarrow \infty$の極限を考えます。$P, Q$が大きいとしてStirlingの公式をつかうと
$n!\sim\sqrt{2\pi n}(\frac{n}{e})^n$より、
\begin{align} \Phi_{-+}(R)=\frac{1}{e^{2\tilde R}}\frac{(PQ)^{\tilde R}}{(\tilde R !)^2} \end{align}
となります。ただし$\tilde R:= \frac{R-1}{2}$です。
ここで$R/P$と$R/Q$は$N\rightarrow \infty$で0になるとします。これは固定した$R$に対し分割数を十分大きくとれば一般的に可能です。
すると
\begin{align} K_{-+}(b;a)=\sum_{R\in \text{odd}}\frac{(PQ)^{\tilde R}}{(\tilde R!)^2} (i\epsilon m)^R \end{align}
となります。

$PQ=\frac{N+M}{2}\frac{N-M}{2} =\frac{N^2-M^2}{4}=\frac{N^2}{4}(1-\frac{M^2}{N^2}) $ですが、ここで
\begin{align} \epsilon N =t_b-t_a,\\ \epsilon c M=x_b-x_a \end{align}
とします。$c$は光の速度、$t_b,t_a$はそれぞれ終状態・始状態の時刻、$x_b, x_a$はそれぞれ終状態・始状態の位置です。自然単位系($c=\hbar=1$にする単位系)をとり、
\begin{align} v^2&:=\frac{M^2}{N^2}=\frac{X^2}{T^2},\\ X&:=x_b-x_a, T:=t_b-t_a \end{align}
を定義します。すると
\begin{align} PQ&=\frac{N^22}{4}(1-v^2)=\lr{\frac{N}{2\gamma}}^2\\ \epsilon&=\frac{T}{N} \end{align}
となります。$\gamma$はいわゆるLorentz因子で
\begin{align} \gamma:=\frac{1}{\sqrt{1-\lr{\frac{v}{c}}^2}} \end{align}
です。以上をつかってまとめると
\begin{align} K_{-+}(b;a)=i\epsilon m\sum_{k=0}^{\frac{N}{2}-1} \frac{(-1)^k}{(k!)^2}\lr{\frac{z}{2}}^{2k} \tag{3} \end{align}
となります。1st kind Bessel functionのテイラー展開は
\begin{align} J_\alpha(z)=\sum_{k=0}^\infty \frac{(-1)^k}{k!\Gamma(k+\alpha+1)} \lr{\frac{z}{2}}^{2k+\alpha} \end{align}
です。$\alpha=0$とすると、$\Gamma(k+1)=k!$より
\begin{align} J_0=\sum_{k=0}^\infty \frac{(-1)^k}{(K!)^2} \lr{\frac{z}{2}}^{2k} \end{align}
なので、Eq.(3)で$N\rightarrow \infty$とすると
\begin{align} K_{-+}(b;a)&\rightarrow i\epsilon m J_0(z),\\ z&:=\frac{Tm}{\gamma} \end{align}
となります。ここで適切に連続極限をとるために、これを$2\epsilon$で割っておきます。
以上より連続極限の$K_{-+}$は
\begin{align} K_{-+}(b,a)=\frac{imJ_0(z)}{2}, \ \ \ z=\frac{Tm}{\gamma} \end{align}
です(Ref.[3])。
$K$の他のcomponentは
\begin{align} \Phi_{++}&= \begin{pmatrix} P-2\\ \frac{1}{2}R \end{pmatrix} \begin{pmatrix} Q-1\\ \frac{1}{2}R-1 \end{pmatrix}\\ \Phi_{--}&= \begin{pmatrix} P-1\\ \frac{1}{2}R-1 \end{pmatrix} \begin{pmatrix} Q-2\\ \frac{1}{2}R \end{pmatrix}\\ \Phi_{+-}&=\Phi_{-+} \end{align}
となります。これらの計算は$\Phi_{-+}$と同様です。
最終的な$K$の表式は
\begin{align} K&:= \begin{pmatrix} K_{++} & K_{+-}\\ K_{-+} & K_{--} \end{pmatrix} =\frac{im}{2} \begin{pmatrix} \frac{i(T+X)}{\tau}J_1(m\tau) & J_0(m\tau)\\ J_0(m\tau) & \frac{i(T-X)}{\tau}J_1(m\tau) \end{pmatrix} ,\\ \tau& :=T/\gamma \end{align}
となります。このように、経路を最初と最後の$+,-$で分類すると、$K$は$2\times 2$行列となることがわかります。

$K$の表式と1+1d Dirac方程式との関係

さて、次にこの$K$が、1+1d Dirac eq.（1+1次元Dirac方程式のこと）を導くことを示します。
最初に示したように1+1d Dirac eq.とは次の微分方程式のことです：
\begin{align} i\partial_t\psi &= -i\sigma_z\partial_x\psi-m\sigma_x\psi,\\ \psi&:= \begin{pmatrix} \psi_1\\ \psi_2 \end{pmatrix}, \sigma_z:= \begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix}, \sigma_x:= \begin{pmatrix} 0&1\\ 1&0 \end{pmatrix} \end{align}
ここで$\partial_t:=\pdiff{}{t}, \partial_x:=\pdiff{}{x}$。
この式は$\psi_1,\psi_2$に対する方程式です。
1+1d Dirac eq.には線形独立な解が2つあり、これらが
\begin{align} \psi^{(1)}&= \begin{pmatrix} \psi^{(1)}_1\\ \psi^{(1)}_2 \end{pmatrix} = \begin{pmatrix} K_{++}\\ K_{+-} \end{pmatrix} =\frac{im}{2} \begin{pmatrix} \frac{i(t+x)}{\tau}J_1(m\tau)\\ J_0(m\tau) \end{pmatrix} ,\\ \psi^{(2)}&= \begin{pmatrix} \psi^{(2)}_1\\ \psi^{(2)}_2 \end{pmatrix} = \begin{pmatrix} K_{-+}\\ K_{--} \end{pmatrix} =\frac{im}{2} \begin{pmatrix} J_0(m\tau)\\ \frac{i(t-x)}{\tau}J_1(m\tau) \end{pmatrix} \end{align}
で与えられることを以下示します。全体にかかる$im/2$のfactorは落として計算していきます。
$\psi^{(1)},\psi^{(2)}$に対するDirac eqs.は
\begin{align} &\text{upper component}: i\partial_t\psi^{(a)}_1 +i\partial_x\psi^{(a)}_1 +m\psi^{(a)}_2=0,\\ &\text{lower component}: i\partial_t\psi^{(a)}_2 -i\partial_x\psi^{(a)}_2 +m\psi^{(a)}_1=0,\\ & \ \ \ a=1,2 \end{align}
です。
$\psi^{(1)}$がDirac eq.を満たすことを示します。まず以下を示します:
\begin{align} i\partial_t\psi^{(1)}_1 +i\partial_x\psi^{(1)}_1 +m\psi^{(1)}_2=0 \end{align}
これは$\psi^{(1)}に対する$Dirac eq.のupper componentです。

同様な計算を$\psi^{(1)}$に対するDirac eq.のlower component、$\psi^{(2)}$に対するeq.のupper・lower componentに対して行えば、$\psi^{(1)},\psi^{(2)}$がDirac方程式を満たすことがわかります。

以上で、$K$が1+1d Dirac eq.を導くことがわかりました。

1+1dの場合の物理的解釈と1+3dへの拡張

このように、経路で分類した確率振幅の4つ組（〜波動関数の行列）が、Dirac方程式を満たします。すなわちDirac方程式に現れる自由度は、経路の「出だし」と「終わり」の経路の向きで場合わけすることにより現れたということです。

ここで疑問なのが、これはspinに対応する自由度なのか？ということですが、その答えはNoのように思えます。
この2段組みの解それぞれは、速度のオペレータの固有状態で、光速で右に動く粒子と左に動く粒子に相当しています。
これはむしろパリティの2段組みのように思えます。

では時間1次元+空間3次元にこの議論を拡張すれば、スピンが現れるでしょうか。実は同様にして1+3d Dirac eq.を導出することができます（Ref.[4]）。
しかしひとつ問題があります。それは、pathの和が収束するためには、粒子の速度が
\begin{align} v\ge 3^{1/2}c\simeq 1.73 \times c \end{align}
を満たさなければならないという条件がつくことです（Ref.[4]）。質量のある粒子が光の速度を超えて移動するという、相対論の因果律に反するような仮定をしなければなりません。
ということで、このような試みは誰もが認める形では成功していないようです。

余談なのですが、現在素粒子論の主流である場の量子論においては、粒子は光速を超えて伝播します。しかし、粒子だけでなく反粒子の伝播も存在し、またこの２つの伝播は区別がつきません。そして、2つの振幅の打ち消しあいにより、ある点$x^\mu=(t,\vec x)$でおこなった観測の影響は、$x$からの光が伝わらないような点の観測には影響しないことが示せます(Ref.[5]のCausalityの章など参照のこと)。このように、場の量子論では、けっこう奇跡的（？）な形で因果律は満たされます。

いづれにせよ、現在では素粒子論は場の量子論（や弦理論などなど）に基づいて議論されるからなのか、このような試みはあまり顧みられなくなっているようです。

まとめ

この記事では、スピンを粒子の運動から導くという試みに関して紹介しました。

この話には続きがあって、1次元イジング模型といわれる模型、またブラウン運動とも関係があります。
いつかその話を書きたいと思います。

おしまい。