マルコフのディオファントス方程式の生き別れの兄弟が可算無限個発見され,その親戚も可算無限個発見された話
こんにちは,ロダンです.前回,方程式$(x+y)^2+(y+z)^2+(z+x)^2=12xyz$の正整数解がマルコフのディオファントス方程式$x^2+y^2+z^2=3xyz$と同じノリで全部見つかりますよみたいな話を こちらの記事 でしました.この方程式$(x+y)^2+(y+z)^2+(z+x)^2=12xyz$をこの記事内では「マルコフのディオファントス方程式の生き別れの兄弟だ!」という風に表現していたのですが,あれから4ヶ月経ち,同じような構造をもつ方程式が他にもたくさん,ざっと可算無限個ほどあることがわかりました.ついでに,ちょっと形が違うが同じような構造を持つ「親戚」のような方程式も可算無限個見つかりました.1匹見つけたらなんとやらってやつですね.いくらなんでも見つかりすぎですが.
今回はその方程式についてお話ししていきたいと思います.この記事は マルコフのディオファントス方程式の生き別れの兄弟が発見された話 の続きものなので,まだ読んでいない方はまずこちらをお読みください.
で,兄弟ってのはどんな方程式なの?
今回扱う方程式は次の方程式です:
\begin{align*} x^2+y^2+z^2+k_1xy+k_2yz+k_3zx=(3+k_1+k_2+k_3)xyz. \end{align*}
ここで,$k_1,k_2,k_3$は$0$以上の整数であればどんな値を入れても良いです(従ってバリエーションは可算無限個存在します).特に$k_1=k_2=k_3=0$のときマルコフのディオファントス方程式,$k_1=k_2=k_3=1$のときに前の記事で取り上げた生き別れの兄弟に相当します.実際,$(x+y)^2+(y+z)^2+(z+x)^2=12xyz$を展開して整理すると$x^2+y^2+z^2+xy+yz+zx=6xyz$となります.
さて,この方程式の解を記述する方法を見てみましょう.まず,$(1,1,1)$はこの方程式の解です.実際,
\begin{align*} 1+1+1+k_1+k_2+k_3=(3+k_1+k_2+k_3)\cdot 1\cdot 1\cdot 1 \end{align*}
となり成立します.次に,マルコフの場合と同様,次のようなルールで別の組を作ることを考えます.
「ルール」:
数の3つ組$(a,b,c)$について,数を一つ選び,その数を次のルールで入れ替える:
$a$を選んだ場合:$\left(\dfrac{b^2+k_2bc+c^2}{a},b,c\right)$,
$b$を選んだ場合:$\left(a,\dfrac{a^2+k_3ac+c^2}{b},c\right)$,
$c$を選んだ場合:$\left(a,b,\dfrac{a^2+k_1ab+b^2}{c}\right)$
とする.
前の記事を読んでくださっている方は「あれ,変形の方法が前と違う?」と思われたかもしれませんが,実はこの変形は表示が違うだけで同じ変形です.前の記事においてマルコフのケースでは$(a,b,c)$を$(3bc-a,b,c)$に変えるとしていましたが,$(a,b,c)$がマルコフの方程式の解であるとき,つまり
\begin{align*}
a^2+b^2+c^2=3abc
\end{align*}
を満たしているとき,$3bc-a=\dfrac{b^2+c^2}{a}$と変形できるのでこの入れ替え操作は$(a,b,c)$を$\left(\dfrac{b^2+c^2}{a},b,c\right)$に変える操作と同じです.マルコフの方程式のケースは今回の方程式の$k_1=k_2=k_3=0$に該当していたので,これを代入してみると確かに上のルールは前の記事のマルコフの方程式の場合の入れ替え操作に一致します.同様に,生き別れの兄弟の方も$(a,b,c)$を$(6abc-a-b-c,b,c)$に変えるとしていましたが,$(a,b,c)$が生き別れの兄弟の方程式の解であるとき,つまり
\begin{align*}
a^2+b^2+c^2+ab+bc+ca=6abc
\end{align*}
を満たしているとき,$6abc-a-b-c=\dfrac{b^2+bc+c^2}{a}$と変形できるのでこの入れ替え操作は$(a,b,c)$を$\left(\dfrac{b^2+bc+c^2}{a},b,c\right)$に変える操作と同じであり,確かに上のルールの$k_1=k_2=k_3=1$の場合に一致します.
さて,では最初に$(1,1,1)$の3番目の1を「ルール」で入れ替えてみましょう.すると,
\begin{align}
\left(1,1,\dfrac{1+k_1+1}{1}\right)=(1,1,k_1+2)
\end{align}
に入れ替わります.こうして,新しい組$(x,y,z)=(1,1,k_1+2)$ができました.さて,これは方程式$x^2+y^2+z^2+k_1xy+k_2yz+k_3zx=(3+k_1+k_2+k_3)xyz$を満たしているでしょうか.確認してみましょう.
$(x,y,z)=(1,1,k_1+2)$とすると,左辺は
\begin{align*}
&1^2+1^2+(k_1+2)^2+k_1+k_2(k_1+2)+k_3(k_1+2)\\
=&k_1^2 + k_2 k_1 + k_3 k_1 + 5 k_1 + 2 k_2 + 2 k_3 + 6
\end{align*}
であり,右辺は
\begin{align*}
&(3+k_1+k_2+k_3)(k_1+2)\\
=&k_1^2 + k_2 k_1 + k_3 k_1 + 5 k_1 + 2 k_2 + 2 k_3 + 6
\end{align*}
となり一致します.正直,最初の段階からもう計算がめんどくさいですね.
もう一回同じ位置で数を入れ替えると元に戻るでしょうか?実際に$(x,y,z)=(1,1,k_1+2)$の$k_1+2$にルールを適用すると,
\begin{align}
\left(1,1,\dfrac{1+k_1+1}{k_1+2}\right)=(1,1,1)
\end{align}
でちゃんと戻ってきました!良さそうですね.前回の記事と同様に,$k_1=0,k_1=1,k_2=2$の場合のツリーを見てみましょう.
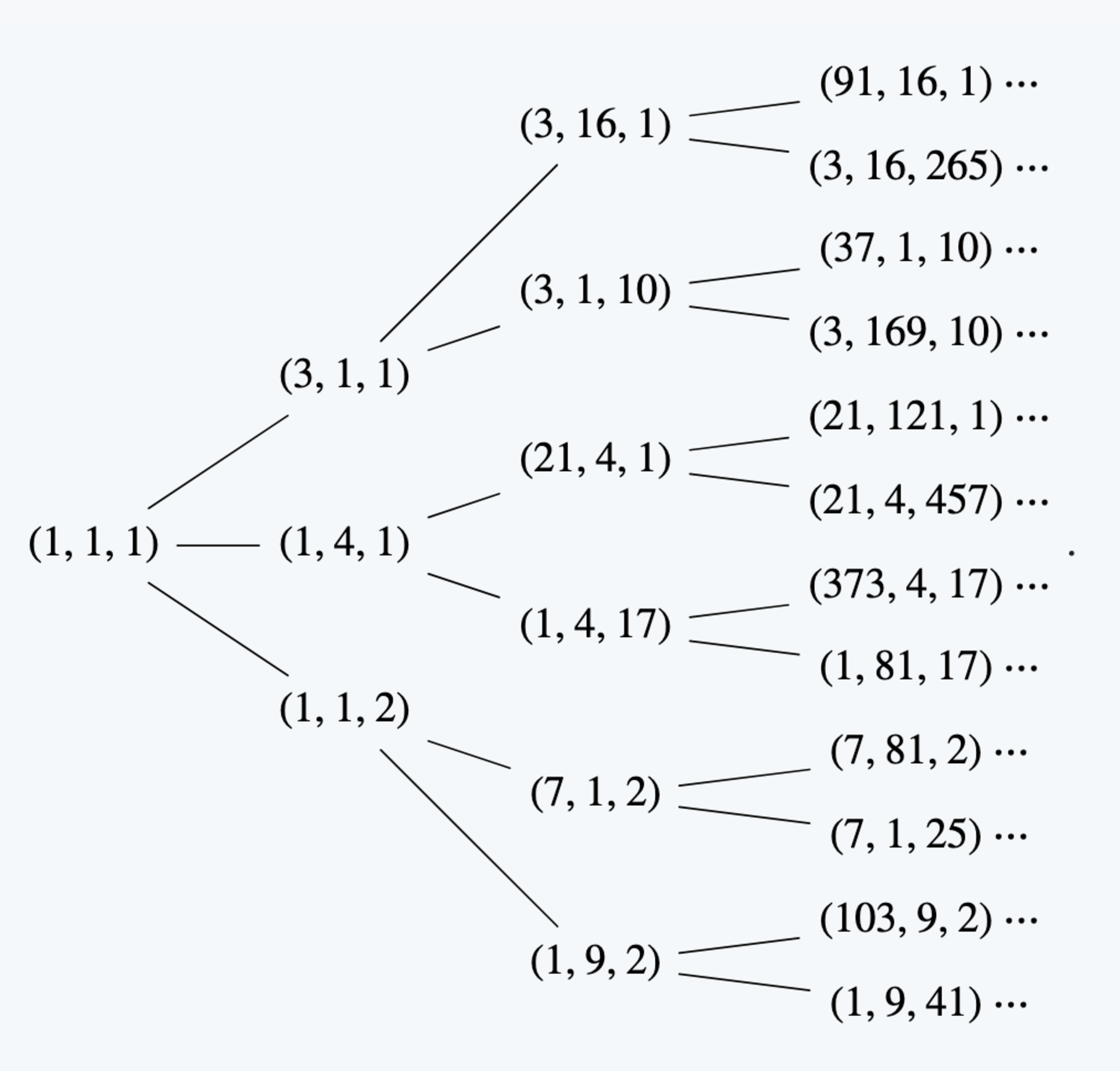 ツリー1
ツリー1
マルコフや生き別れの兄弟の時と違い,$x,y,z$の条件が対称的ではないので,$(1,1,1)$からいきなり三又に分かれたものを考えます.$k_1=k_2=k_3$のときは最初の3分岐のうちの2つの枝には残りの1つの枝に現れる整数の3つ組を並べ替えたものが現れるので前回の記事では省略していましたが,今回は省略しません.さて,この木についてマルコフの場合と全く同様に次が成立します.
木に現れる整数の3つ組は,
- 全て正の整数の3つ組である.
- 全て方程式\begin{align*} x^2+y^2+z^2+k_1xy+k_2yz+k_3zx=(3+k_1+k_2+k_3)xyz. \end{align*}の解である.
- 同じ位置の整数を「ルール」をつかって2回続けて変化させると,元に戻ってくる.
さらにこの木についてもマルコフの木と同様に「『ルール』によって方程式の全ての正整数解を列挙することができてしまう」という次の定理が成立しています.これがこの記事の1つ目のメイン定理です.
全ての
\begin{align*}
x^2+y^2+z^2+k_1xy+k_2yz+k_3zx=(3+k_1+k_2+k_3)xyz.
\end{align*}
の整数解は,この木のどこかに,必ず1回だけ現れる.
証明は[2]をみてください.大筋はマルコフや生き別れの兄弟の場合とそんなに変わりません.
さて,マルコフや生き別れの兄弟のケースでは次の予想が立てられていたのでした.
任意のマルコフ数$c$に対して,$c$を最大数とするような$x^2+y^2+z^2=3xyz$の解が(数の順番による差を除いて)ただ一つ存在する.
これは一般のケースでは成立しないことがすぐにわかります.たとえば上で紹介した$k_1=0,k_2=1,k_3=2$のとき,$(1,81,17)$と$(7,81,2)$が解になっていることが見て取れますが,これらは共に$81$を最大数として持つ解であり,3つの数の順番を入れ替えても一致することはありません.ちなみにマルコフ方程式の場合
素数の冪で表される任意のマルコフ数$c$に対して,$c$を最大数とするような$x^2+y^2+z^2=3xyz$の解が(数の順番による差を除いて)ただ一つ存在する.
というような予想の部分的解決がありますが,先の例はそれすらも一般のケースでは成り立ってくれないということを示しています.
ちなみに,$k_1=k_2=k_3=2$の場合はちょっと面白いことが成り立ちます.まずはツリーを見てみましょう.
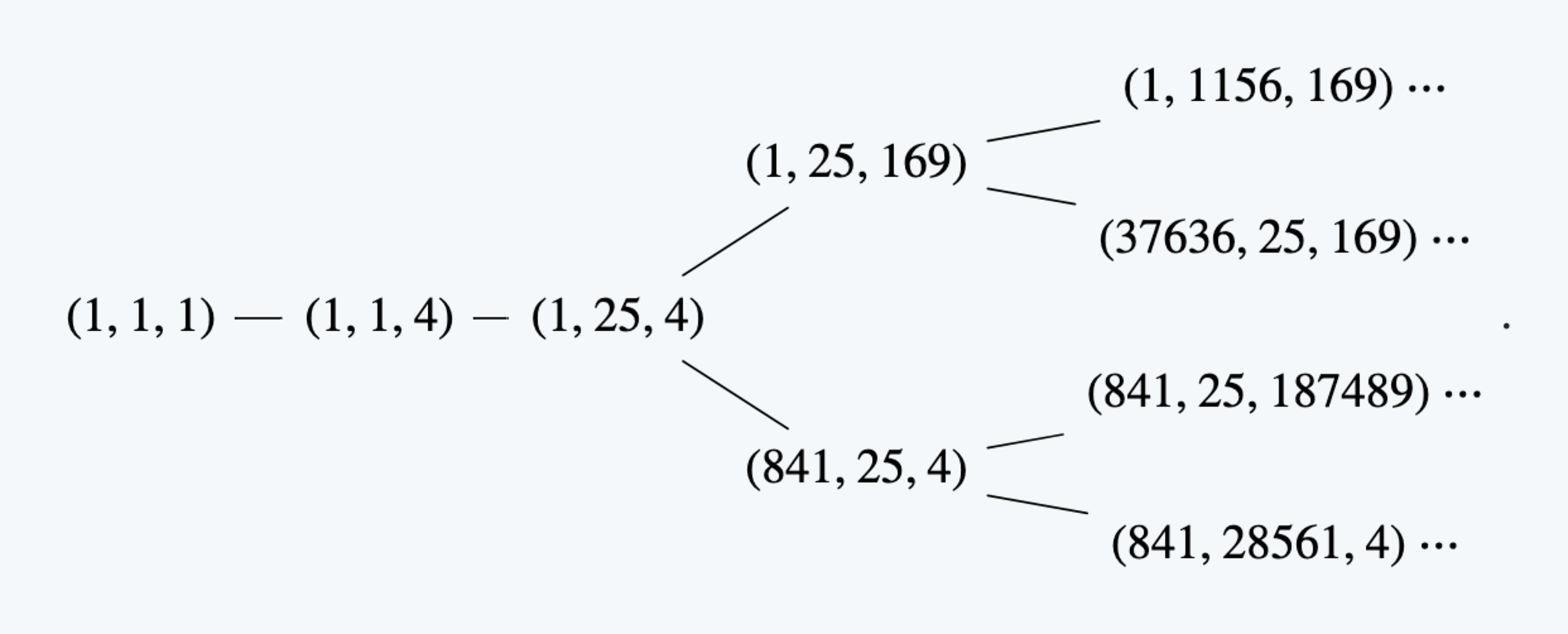 ツリー2
ツリー2
対称式なので前回の記事のマルコフの木などと同様,解が重複する枝は省略しています.これだけみてても何が面白いかわからないと思うので,マルコフの木と比較してみましょう.
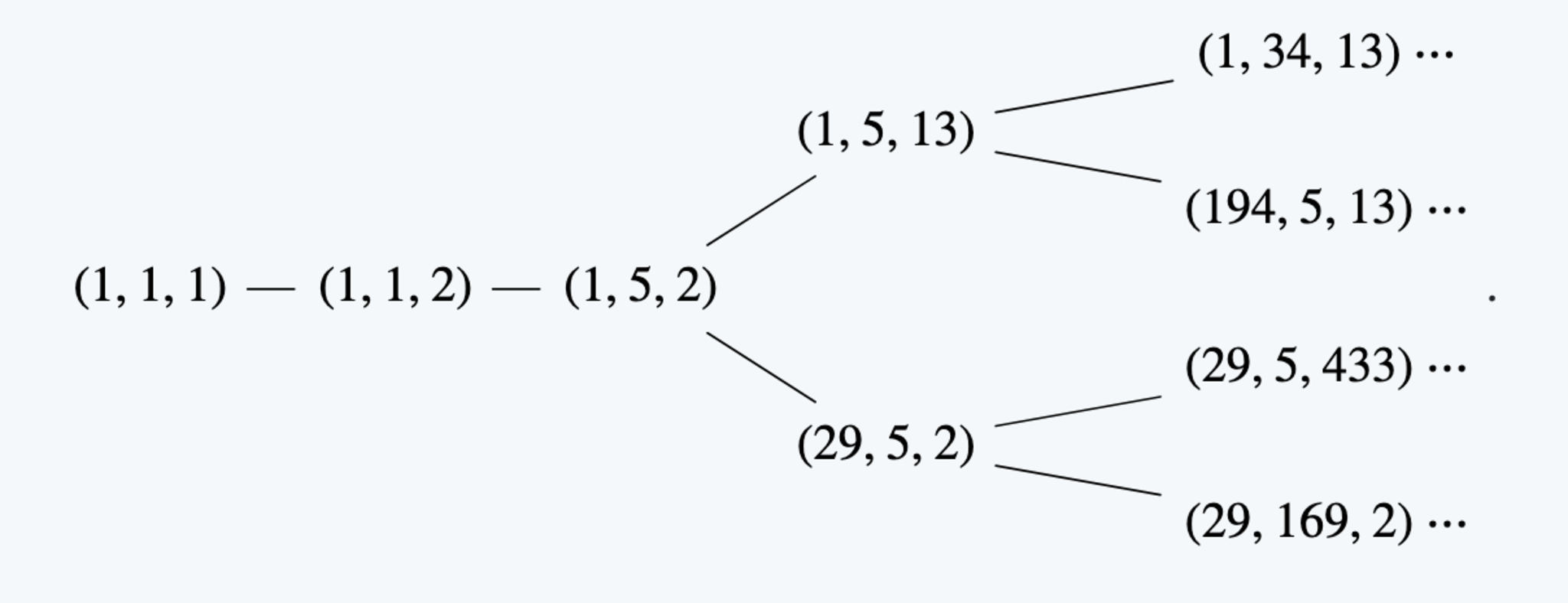 ツリー3
ツリー3
よーく見比べてみると,上の木の3つ組は下の木の3つ組みの各成分を全て2乗したものであることがわかります.実は,次の定理が成り立ちます.
$(x,y,z)=(a,b,c)$がマルコフの方程式の整数解であるとき,$(X,Y,Z)=(a^2,b^2,c^2)$は
方程式
\begin{align*}
X^2+Y^2+Z^2+2XY+2YZ+2ZX=9XYZ.
\end{align*}
の整数解である.逆に$(X,Y,Z)=(A,B,C)$がこの方程式の整数解であるとき,$(x,y,z)=(\sqrt{A},\sqrt{B},\sqrt{C})$はマルコフの方程式の整数解である.
この事実は$(a^2,b^2,c^2)$の1つの元を$k_1=k_2=k_3=2$のときのルールに従って変えるとちょうどマルコフのケースの2乗の値$\left(\left(\dfrac{b^2+c^2}{a}\right)^2,b^2,c^2\right)$が出てくるという事実から帰納的に従います.生き別れの兄弟,意外とマルコフ数に近いところにいたんですね.
さらに,これらの新たに見つかった可算無限個のマルコフの兄弟の中には,実は前回紹介した兄弟よりも一足早く人間社会デビューしていた方程式がいたことがわかりました.それが$k_1=k_3=2,k_2=0$のケースです.この方程式の正整数解を全て見つける方法は,Philipp Lampeさんという方の論文[3, Lemma 2.7]で今回紹介している「ルール」(の特別な場合)を用いて2016年に証明されていました.このように,今回発見した可算無限個の兄弟の中には既にこの世に姿を現している方程式が他にもあるかもしれません.もし知っている方がいればコメント欄などで教えていただけると嬉しいです.
じゃあマルコフの方程式の親戚って何?
次に,親戚の方程式について述べることにしましょう.前節の最後に,生き別れの兄弟は$k_1=k_3=2,k_2=0$の場合については実は既にLampeさんによって発見されていたという話をしましたが,このことが記してある論文[3]のメインテーマは生き別れの兄弟$k_1=k_3=2,k_2=0$の方程式というわけではありませんでした.この論文において,生き別れの兄弟$k_1=k_3=2,k_2=0$の方程式は次の定理を証明するために使われています:
次のようなルールを考える.
「ルール2」:
数の3つ組$(a,b,c)$について,数を一つ選び,その数を次のルールで入れ替える:
$a$を選んだ場合:$\left(\dfrac{b^4+c^4}{a},b,c\right)$,
$b$を選んだ場合:$\left(a,\dfrac{a+c^2}{b},c\right)$,
$c$を選んだ場合:$\left(a,b,\dfrac{a+b^2}{c}\right)$
とする.このとき,$(1,1,1)$から上記のルールで数を繰り返し入れ替えた三つ組は,方程式
\begin{align*}
x^2+y^4+z^4+2xy^2+2z^2x=7xy^2z^2
\end{align*}
の正整数解であり,逆に全ての正整数解は$(1,1,1)$から上記のルール2で繰り返し数を入れ替えることで得ることができる.
この定理に現れる方程式
\begin{align*}
x^2+y^4+z^4+2xy^2+2z^2x=7xy^2z^2
\end{align*}
は,$X=x,Y=y^2,Z=z^2$と置き直すことで
\begin{align*}
X^2+Y^2+Z^2+2XY+2ZX=7XYZ
\end{align*}
となり,マルコフの生き別れの兄弟の$k_1=k_3=2,k_2=0$のケースに一致します.この定理の証明の概要としては,この方程式の正整数解$(X,Y,Z)$の$Y$と$Z$は実は全て整数の2乗という形で記述できるので,これと正整数解$(X,Y,Z)$を全て記述する「ルール」のアルゴリズムを使って
\begin{align*}
x^2+y^4+z^4+2xy^2+2z^2x=7xy^2z^2
\end{align*}
の方程式の正整数解が全て計算できます,というものでした.従って定理5の「ルール2」も,やはり命題1と同じような命題が成立します.上記の方程式の正整数解も,マルコフの方程式の直接的な一般化ではないにせよそれと同じような構造を持つことが分かったので,これをマルコフの方程式の「親戚」とでも呼ぶことにしましょう.
さて,今我々は$k_1=k_3=2,k_2=0$以外のケースでも「ルール」によって全ての正整数解を記述できることを知っています.ということはこの定理5も一般化できるのではないか?と思うわけです.そしてそれは実際に次の形で可能でした.
次のようなルールを考える.
「ルール3」:
数の3つ組$(a,b,c)$について,数を一つ選び,その数を次のルールで入れ替える:
$a$を選んだ場合:$\left(\dfrac{b^4+kb^2c^2+c^4}{a},b,c\right)$,
$b$を選んだ場合:$\left(a,\dfrac{a+c^2}{b},c\right)$,
$c$を選んだ場合:$\left(a,b,\dfrac{a+b^2}{c}\right)$
とする.このとき,$(1,1,1)$から上記のルールで数を繰り返し入れ替えた三つ組は,方程式
\begin{align*}
x^2+y^4+z^4+2xy^2+ky^2z^2+2z^2x=(7+k)xy^2z^2
\end{align*}
の正整数解であり,逆に全ての正整数解は$(1,1,1)$から上記のルール3で繰り返し数を入れ替えることで得ることができる.
上記の方程式を親戚の方程式の証明と同様に$X=x,Y=y^2,Z=z^2$と置き直してやると,
\begin{align*}
X^2+Y^2+Z^2+2XY+kYZ+2ZX=(7+k)XYZ
\end{align*}
という方程式が出てきます.これは一般化された生き別れの兄弟の$k_1=k_3=2,k_2=k$の場合に一致します.このケースでもやはり正整数解$(X,Y,Z)$の$Y$と$Z$は全て整数の2乗の形で記述されるうえに,我々はこの方程式の正整数解を全て列挙するアルゴリズムを定理2により知っているので,定理5と同じ方法を取ることによって定理6を証明することができます(詳細は[2]や[3]をご覧ください).以上から,このマルコフの「親戚」に相当する方程式もやはり可算無限個あることがわかったのでした.
ちなみに,$k=1$のときに「ルール3」のアルゴリズムによって生成される木は次のようなものになります.
 ツリー4
ツリー4
終わりに〜さらなる仲間の発見に向けて〜
これらの一般化の話を見たとき,「いったいこんなのをどういうきっかけで見つけてくるんだ?」と思ったことと思います.実は,この一般化を発見した論文[2]には,「ルール」「ルール2」「ルール3」は全て「一般化クラスター代数」と呼ばれる代数において定まる「変異」と呼ばれる変換の特別な場合であるという記述があります(「また『変異』か,お前の記事は本当にそればっかりだな」と思った方,いつも私の記事を読んでいただきありがとうございます).ここでは変異の細かい定義については言及を避けますが,これらの定理たちはまず変異から得られる3つ組みの整数ツリーが先にあって,これに合う方程式を見つけるという形で全て得られています.変異が作り出す組み合わせ構造は,今回紹介しているもの以外にも様々なものがあり,他の変異構造から生まれる整数組も同じようにして対応する方程式を見つけられる可能性があります.どういう構造が整数解をもつ可能性があるのか?ということについては,論文[2]の最後の方に記述があるので,皆さんもこれを機に考えてみてはいかがでしょうか.私も,また新しい知見が得られたら記事を書こうと思っています.というわけで,ここまでお読みいただきありがとうございました.