文献あり

マルコフのディオファントス方程式の生き別れの兄弟が発見された話

3810

こんにちは，ロダンです．今日は最近論文[2]によって発見された，マルコフのディオファントス方程式の生き別れの兄弟について紹介したいと思います．

そもそもマルコフのディオファントス方程式って何？

まずはまるで「お馴染みの！」とでも言いたげな感じでここまで言及してきた「マルコフのディオファントス方程式」の説明から入ることにします．マルコフのディオファントス方程式とは，
$\begin{array}{r} x^{2} + y^{2} + z^{2} = 3 x y z \end{array}$
という方程式のことを指します．この方程式は正の整数解に非常に特徴的な構造が見られるという点と解決が難しい予想が存在するという点で，昔から多くの数学者を惹きつけてきました．まずはその構造と予想について説明しましょう．

最初に，この方程式の正の整数解には結構分かりやすいものがあります． $(x, y, z) = (1, 1, 1)$ です．

$\begin{array}{r} 1 + 1 + 1 = 3 \cdot 1 \cdot 1 \cdot 1 \end{array}$

で確かに成り立ってますね．では，この3つ組から，次のルールで別の組を作ることを考えます．

「ルール」：
数の3つ組 $(a, b, c)$ について，数を一つ選び，その数を

（選ばなかった2つの数の積の3倍） $-$ （選んだ数）

と入れ替える．すなわち，

$a$ を選んだ場合： $(3 b c - a, b, c)$ ,
$b$ を選んだ場合： $(a, 3 a c - b, c)$ ,
$c$ を選んだ場合： $(a, b, 3 a b - c)$

とする．

$(1, 1, 1)$ はどの数を選んでも $1$ なので，とりあえず3番目の $1$ を上の「ルール」で交換してみましょう．ルールに則ると，3番目の $1$ は $3 \cdot 1 \cdot 1 - 1 = 2$ に入れ替わります．こうして新しい組 $(x, y, z) = (1, 1, 2)$ ができました．さて，ここで重要なのは，この3つ組は実はマルコフのディオファントス方程式 $x^{2} + y^{2} + z^{2} = 3 x y z$ を満たしているということです．実際，左辺は $1^{2} + 1^{2} + 2^{2} = 6$ で，右辺は $3 \cdot 1 \cdot 1 \cdot 2 = 6$ でちゃんと成立しています．

偶然なのか？もう一回やってみましょう．今度は，今しがたできた $(x, y, z) = (1, 1, 2)$ から，2番目の1を選んで「ルール」に則って新しい組をつくります．すると，
$\begin{array}{r} (1, 3 \cdot 1 \cdot 2 - 1, 2) = (1, 5, 2) \end{array}$

となります．では $(x, y, z) = (1, 5, 2)$ はマルコフのディオファントス方程式 $x^{2} + y^{2} + z^{2} = 3 x y z$ を満たしているのでしょうか？実際に計算してみると分かりますが，両辺とも $30$ になってちゃんと満たされることがわかります．どうやら偶然ではないようですね？では次に，今変えた2番目の値を，もう一度「ルール」に則って変えてみましょう．

$\begin{array}{r} (1, 3 \cdot 1 \cdot 2 - 5, 2) = (1, 1, 2) \end{array}$

これはマルコフのディオファントス方程式を満たしていますか？計算するまでもないですよね，だってこの $(x, y, z) = (1, 1, 2)$ という組はさっき見ましたからね．ん？さっき見た？どういうことでしょう． $(1, 1, 2)$ からルールを使って $(1, 5, 2)$ にしたものを，もう一度同じルールで同じ位置の整数を変化させると，元に戻ってきているということになってませんか？さあ，果たしてこれも偶然なのでしょうか．とりあえず，この操作をもう何回か繰り返してみましょう．ということでできたものがこちら．

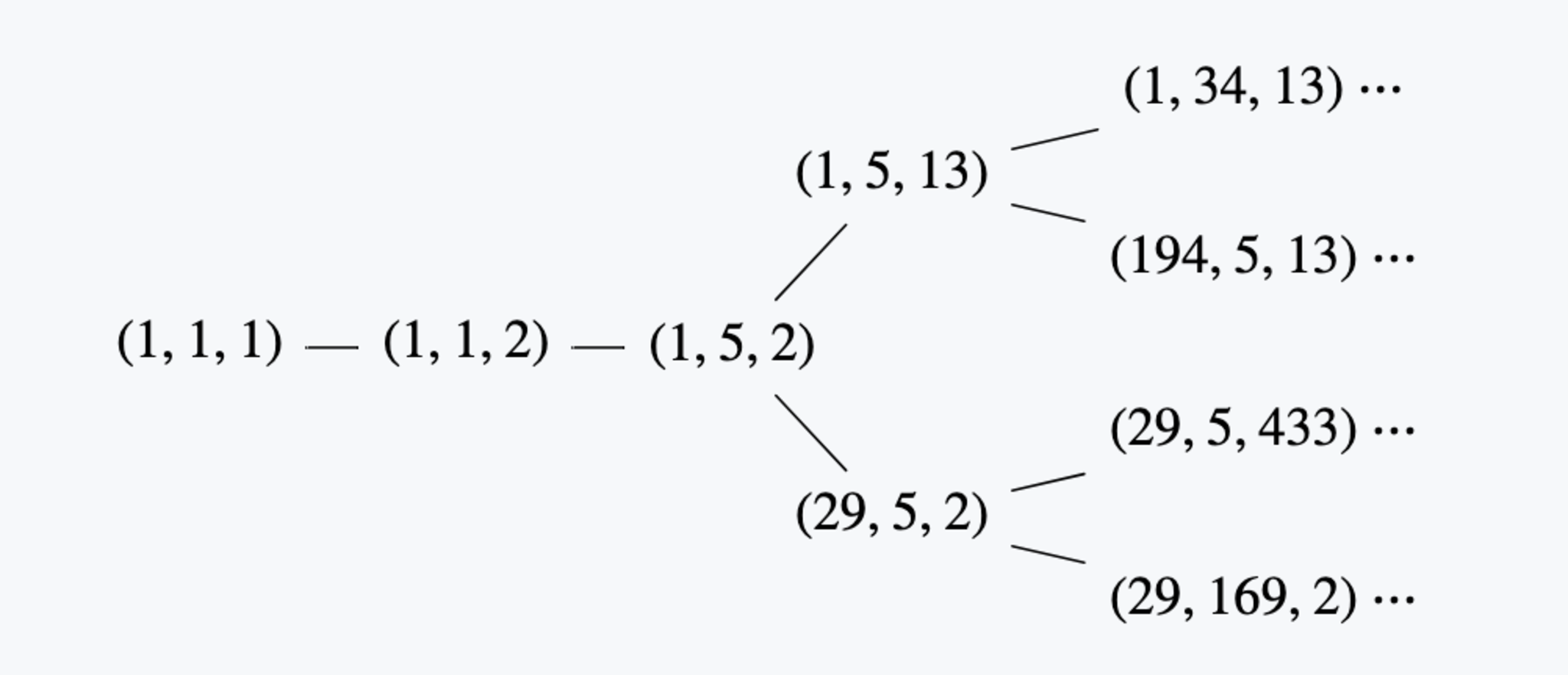マルコフの木

この図は2つの3つ組が「ルール」によって変化するとき，その2つの3つ組が辺で結ばれているような図になっています．ただし， $(1, 1, 1)$ はどの $1$ を変化しても出てくる数は変わらないし， $(1, 1, 2)$ もどっちの $1$ を変化させても結果は一緒なので，その部分は省略してあります．さて，たとえばこの図によると $(1, 5, 2)$ はルールに則って3番目の成分を入れ替えると $13$ になるようですね．実際，

$\begin{array}{r} (1, 5, 3 \cdot 1 \cdot 5 - 2) = (1, 5, 13) \end{array}$

で，これは正しいことがわかります．これがマルコフのディオファントス方程式の解になってるかも確認しておきましょう． $(x, y, z) = (1, 5, 13)$ を方程式の左辺に代入すると $1 + 5^{2} + 13^{2} = 195$ , 右辺に代入すると $3 \cdot 1 \cdot 5 \cdot 13 = 195$ で確かになっています．ではもう1回 $(1, 5, 13)$ の3番目の成分をルールに則って変化させてみましょう．

$\begin{array}{r} (1, 5, 3 \cdot 1 \cdot 5 - 13) = (1, 5, 2) \end{array}$

むむむ，さっきと同じく，元の $(1, 5, 2)$ に戻ってきていますね．つまり上の図の辺は左から右への一方通行ではなく，右から左へも同じルールで移動できるみたいです．この図，90°起こすとなんだか木に見えるので，マルコフの木とでもしておきましょう．

さて，これまでの観察で得られた推測を，命題としてまとめておきましょう．

マルコフの木に現れる整数の3つ組は，

全て正の整数の3つ組である．
全てマルコフのディオファントス方程式 $x^{2} + y^{2} + z^{2} = 3 x y z$ の解である．
同じ位置の整数を「ルール」をつかって2回続けて変化させると，元に戻ってくる．

この命題1は正しいです．演習問題としますので，頑張ってみてください．
さて，このマルコフの木のすごいところは，この木に現れる3つ組が，マルコフのディオファントス方程式 $x^{2} + y^{2} + z^{2} = 3 x y z$ の正の整数解を全部尽くしちゃっているという事実です．つまり，次の定理が成立しています．

全てのマルコフのディオファントス方程式の正の整数解は，マルコフの木のどこかに，必ず1回だけ現れる（ただし，同じ数の組み合わせで順番が違う3つ組は同じものとして扱う．たとえば， $(1, 2, 5)$ と $(1, 5, 2)$ は同一視する）．

これもやや難しいですが，初等的な整数論の範囲内です．ガッツがある人は解いてみましょう．この答えはAignerの本[1]のSection 3.1に書いてあるので，回答が知りたい人はそこをみてください（ただし英語です）．

「特定の方程式の（正）整数解を全て見つける」という問題はディオファントス問題と呼ばれ，古来紀元前からいろんな人がいろんな方程式に対して取り組んできた，数学において最も根源的な1つのテーマなのですが，マルコフのディオファントス方程式に関してはこのマルコフの木と定理2がその問題の1つの回答となっているわけです．

また，このマルコフの木に現れる正の整数はマルコフ数と呼ばれ，連分数展開や双曲幾何，モジュラー群などとも深い関わりがあり，現在もなお数学者の興味の対象として親しまれています．

さらに，このマルコフの木には，次のような未解決予想もあります．この予想は1913年にフロベニウスが言及したとされる，マルコフの単一性（一意性）予想と呼ばれる予想です．

任意のマルコフ数 $c$ に対して， $c$ を最大数とするようなマルコフディオファントス方程式の解が（数の順番による差を除いて）ただ一つ存在する．

この予想は100年経った現在もまだ解かれておらず，この予想の解決のために数学者たちが日夜努力を続けているというわけです．

マルコフのディオファントス方程式の生き別れの兄弟

さて，ここまでの話については正直Wikipediaとかを見て貰えばいい感じのことが書いてあるので，これをメインに据えて記事を書くほどのことではないと思っています．私が今回本当に書きたいのはここから先の話です．最近（2021年9月）になって，先述のマルコフ方程式と同じような正整数解の構造を持つ方程式が発見されました．それは次のような方程式です．

$\begin{array}{r} (x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z \end{array}$

この方程式に注目した研究は（私の知る範囲では）ほとんどないため，この方程式にはまだ名前らしい名前がありません（と思っています）．

さて，ここからはこの方程式がなぜ「マルコフのディオファントス方程式の生き別れの兄弟」と呼べる方程式なのかどうかを説明していこうと思います．まず，この方程式はマルコフの場合と同様， $(x, y, z) = (1, 1, 1)$ が解になっています．実際に確かめてみると，

$\begin{array}{r} (1 + 1)^{2} + (1 + 1)^{2} + (1 + 1)^{2} = 12 = 12 \cdot 1 \cdot 1 \cdot 1 \end{array}$

となり成立します．次に，マルコフの場合と同様，次のようなルールで別の組を作ることを考えます．一つ前の「ルール」と区別するため，「ルール2」としておきます．

「ルール2」：
数の3つ組 $(a, b, c)$ について，数を一つ選び，その数を

（選ばなかった2つの数の積の6倍） $-$ （a,b,cの総和）

と入れ替える．すなわち，

$a$ を選んだ場合： $(6 b c - a - b - c, b, c)$ ,
$b$ を選んだ場合： $(a, 6 a c - a - b - c, c)$ ,
$c$ を選んだ場合： $(a, b, 6 a b - a - b - c)$

とする．

マルコフの場合と同じく，最初は $(1, 1, 1)$ の3番目の1を「ルール2」で入れ替えてみましょう．これに則ると，
$\begin{array}{r} (1, 1, 6 \cdot 1 \cdot 1 - 1 - 1 - 1) = (1, 1, 3) \end{array}$
に入れ替わります．こうして，新しい組 $(x, y, z) = (1, 1, 3)$ ができました．さて，これは方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ を満たしているでしょうか．確認してみましょう．

$(x, y, z) = (1, 1, 3)$ とすると，左辺は $(1 + 1)^{2} + (1 + 3)^{2} + (3 + 1)^{2} = 36$ であり，右辺は $12 \cdot 1 \cdot 1 \cdot 3 = 36$ で確かに満たしています．

マルコフの場合はもう一回同じ位置で数を入れ替えると元に戻りましたが，それはどうでしょう？実際に $(x, y, z) = (1, 1, 3)$ の $3$ にルールを適用すると，
$\begin{array}{r} (1, 1, 6 \cdot 1 \cdot 1 - 1 - 1 - 3) = (1, 1, 1) \end{array}$
でちゃんと戻ってきました！他の場合も計算してみましょう．マルコフの場合と同様，ツリーを考えてみます．

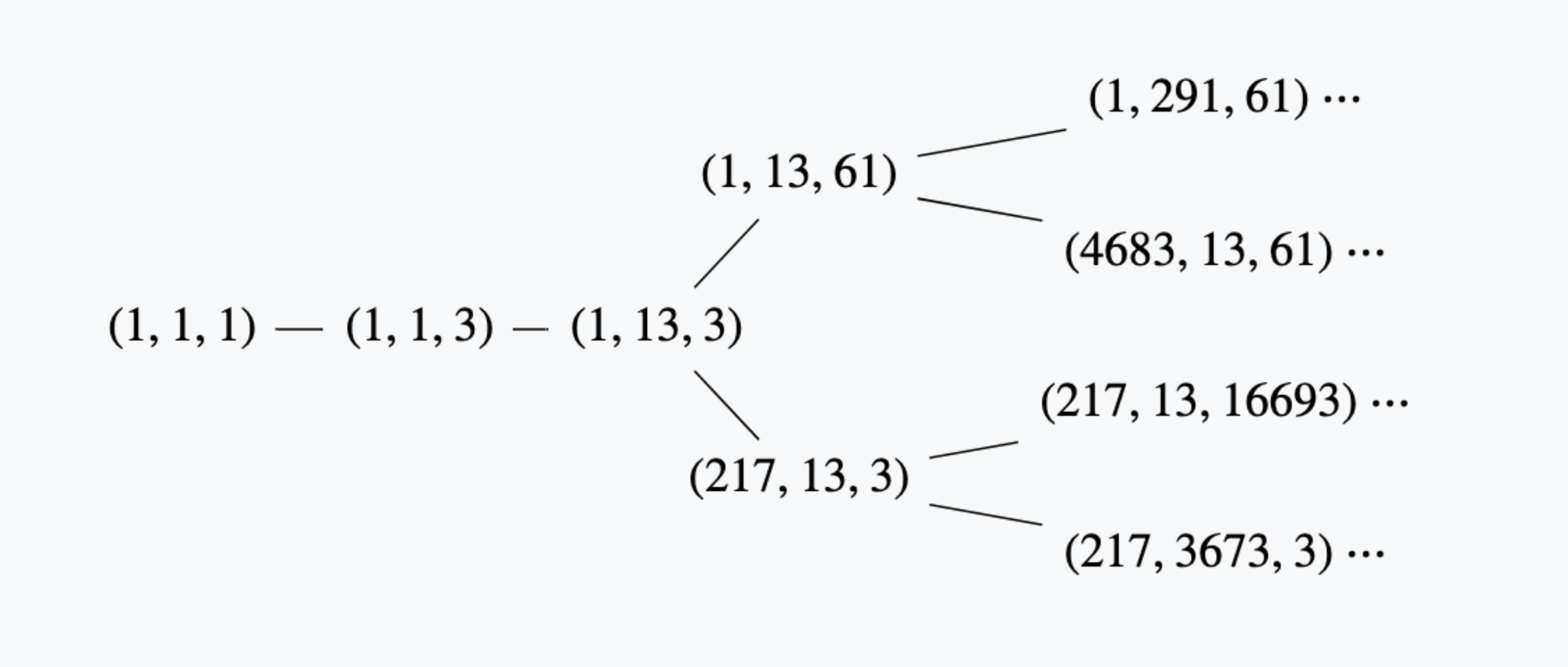名無しの木

たとえば $(1, 13, 3)$ を考えてみましょう．まずこれが方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の解になっていることを確かめます．実際に計算してみると，左辺が $(1 + 13)^{2} + (13 + 3)^{2} + (3 + 1)^{2} = 468$ , 右辺が $12 \cdot 1 \cdot 13 \cdot 3 = 468$ で両辺一致しているのでこれは解です．さらに，「ルール2」で3番目の数 $3$ を変えると

$\begin{array}{r} (1, 13, 6 \cdot 1 \cdot 13 - 1 - 13 - 3) = (1, 13, 61) \end{array}$

となっており，また $(x, y, z) = (1, 13, 61)$ を方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ に代入してみると左辺右辺それぞれ

$\begin{aligned} (1 + 13)^{2} + (13 + 61)^{2} + (61 + 1)^{2} & = 9516 \\ 12 \cdot 1 \cdot 13 \cdot 61 & = 9516 \end{aligned}$
となって確かにこれは方程式の解になっています．
さらに，もう一度「ルール2」で3番目の数を変えると

$\begin{array}{r} (1, 13, 6 \cdot 1 \cdot 13 - 1 - 13 - 61) = (1, 13, 3) \end{array}$

で元に戻ってきています．どうやらマルコフの場合と同じようなことが考えられそうですね．
そこで，上の木についてもう少し考察していきましょう．ただ，先述の通り方程式に名前がないのでこの木にも名前がありません．そこで便宜上名無しの木と名付けましょう．もしこの方程式についての先行研究をご存知の方はコメント等でお知らせいただけますと幸いです．

この木について，マルコフの場合と全く同様に次が成立します．

名無しの木に現れる整数の3つ組は，

全て正の整数の3つ組である．
全て方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の解である．
同じ位置の整数を「ルール2」をつかって2回続けて変化させると，元に戻ってくる．

この命題も命題1が証明できた方は証明できると思います．さて，この木についてもやはり次の定理が成立しています．

[2,Theorem 1.1]

全ての $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の整数解は，名無しの木のどこかに，必ず1回だけ現れる（ただし，同じ数の組み合わせで順番が違う3つ組は同じものとして扱う）．

また，この木に現れる正の整数を便宜上名無し数と呼ぶことにすると，これについてもマルコフの単一性予想と全く同じ予想がたちます．

任意の名無し数 $c$ に対して， $c$ を最大数とするような $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の解が（数の順番による差を除いて）ただ一つ存在する．

比較してみればみるほど，挙動がマルコフのディオファントス方程式にそっくりですね．こちらにはまだ連分数展開やその他マルコフ数にみられるような他分野との関連性は明らかにされていませんが，おそらくこれから研究成果が出てくるものだと予想しています．

ここまで挙動が似ているのにも関わらず，マルコフの方は長きにわたり数学者の興味の対象としてあり続けた一方，こちらの方程式は長らく発見されず，最近になって日の目を見ることになりました．

これはまさに，同じ数学という星のもとに生まれながら離れ離れになり，まったく違う境遇を過ごし，100年以上という長き時間の後に同じ数論のフィールドで感動の再会を果たした生き別れの兄弟と言えるのではないでしょうか．

ということで，今回はマルコフのディオファントス方程式に性質がそっくりな方程式が発見されたお話でした．ここまで読んでくださりありがとうございました．

追記（2022/2/21)

本記事中に，

こちらにはまだ連分数展開やその他マルコフ数にみられるような他分野との関連性は明らかにされていませんが，おそらくこれから研究成果が出てくるものだと予想しています．

とありますが，現在はマルコフ数に見られるような，曲面の三角形分割との対応，グラフのパーフェクトマッチングや連分数展開との関連性についても明らかになりました．詳しくは引用元の論文[2]の第3版か解説動画 https://www.youtube.com/watch?v=40QVYHZpUb8 をご覧ください．

また，今年の1月末にマルコフの方程式やこの方程式と同じような構造を持つ方程式がさらに見つかったという論文が発表されました．詳しくはマルコフのディオファントス方程式の生き別れの兄弟が可算無限個発見され，その親戚も可算無限個発見された話をご覧ください．

本記事の定理4（原論文[2]のTheorem 1.1）を背景として持つ問題が，高校数学を取り扱うサイトである『有名問題・定理から学ぶ数学』様に取り上げられました．
https://wkmath.org/vie-f.html#q-mar-tpl-anal
こちらも合わせてご覧ください．

また， $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ の正整数解 $(x, y, z)$ を小さい順に並べた整数列がオンライン整数列に追加されていました．
https://oeis.org/A351372
このページでリファレンスされている論文は現在は原論文[2]のみですが，関連論文がでるとこのページに追加されることが予想されます．

さらに追記（2022/8/9)

この記事がtsujimotter様のYouTube動画にて紹介されました．メインはマルコフ方程式とマルコフ数についての紹介動画となっております．是非ご視聴ください．
https://www.youtube.com/watch?v=PgGckE4Qw64

さらにさらに追記（2024/5/13)

ギリシャで2024年2月24日に行われた第41回全国数学オリンピック「アルキメデス」（原題：41ης ΕΘΝΙΚΗΣ ΜΑΘΗΜΑΤΙΚΗΣ ΟΛΥΜΠΙΑΔΑΣ«O ΑΡΧΙΜΗΔΗΣ»）で次のような問題が出題されました．

(Θέματα τάξεων Γυμνασίου　Πρόβλημα 4)

Να αποδείξετε ότι υπάρχουν άπειρες τριάδες θετικών ακέραιων αριθμών $(x, y, z)$ τέτοιες ώστε
$\begin{array}{r} x^{2} + y^{2} + z^{2} + x y + y z + z x = 6 x y z . \end{array}$

日本語訳は以下の通りです(Google翻訳で調べているので，間違っていたら教えてください)．

(中等部　問題4)

次の方程式の正整数解 $(x, y, z)$ が無限個存在することを示せ：
$\begin{array}{r} x^{2} + y^{2} + z^{2} + x y + y z + z x = 6 x y z . \end{array}$

このブログ中では方程式 $(x + y)^{2} + (y + z)^{2} + (z + x)^{2} = 12 x y z$ を扱っていますが，左辺を展開して両辺2で割ると明らかに上の式に一致します．そして，この問題は上述したように，「ルール２」を繰り返し用いることで解決することができます．解の個数の無限性は，新しく現れる数が他の２つの数より大きいことから示されます．