置換積分と座標独立性

積分に関するちょっとしたお話

積分が座標変換に対して不変ということは、つまりは座標のとり方に依存しないということです。
多様体のお話にもちこむとその視点が明確になるなぁ、という、まあ教科書によく書いてようなことをつらつら述べます。

けっこう適当な、私の感覚も書いてあります。また多様体論に言及しますが、そのあたりのこと全く詳しくないので、へんなこと言っていたらすみません＆良ければご指摘ください。

本記事はRef.[1-3]を参考にして書かれています。
以下の内容におかしな点があれば、それはすべて私の理解不足や勝手な妄想に基づくものであり、これら教科書に罪はありません（名著ばかりなので当たり前ですが）。

区分求積の任意性と置換積分

高校数学で区分求積法を習います。
これは関数$f(x)$が$x$軸と囲う面積を、横の長さ一定の細かい長方形の集まりで近似して、それを足し合わせ積分を計算する方法です。図にすればこんな感じです：

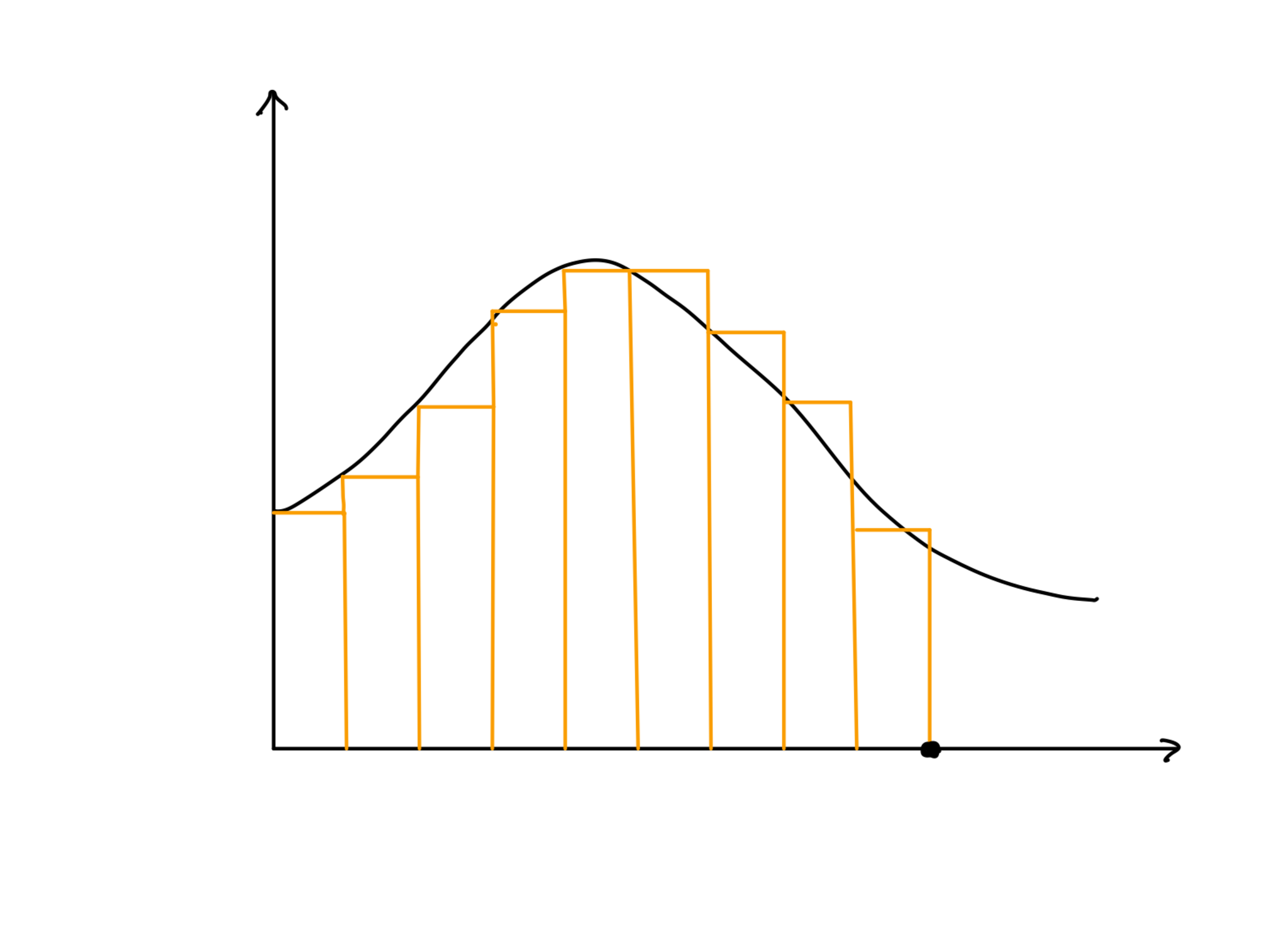区分求積：等分割した例

でも横の長さ一定の長方形にする必要はありません。長方形の横の長さがどれも十分短ければ、こんな切り方でもいいです：

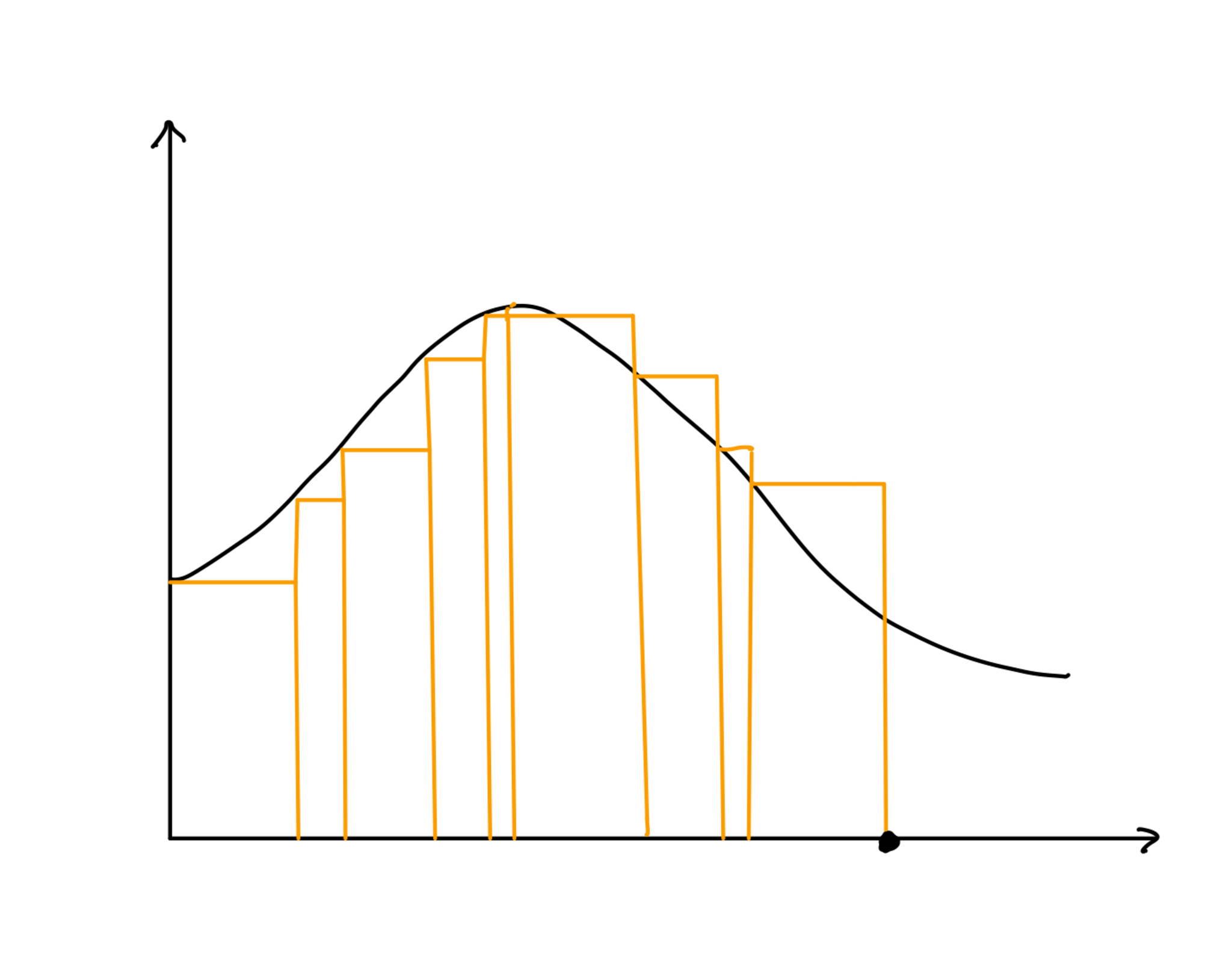区分求積（？）：等分割ではない例

この議論を一般化します。
ある$t$というパラメータと、これに依存する任意の連続関数$g(t)$を導入します。
この$g(t)$は、上図の$x$の区切り方を与える関数です。すなわち$g(t_i) (i=0,...,N-1)$が、$i$番目の長方形の底辺の区切りの位置だとします。ここで$t_i \equiv i \Delta t, x_i\equiv i\Delta x$とすると、$\Delta x$と$\Delta t$がどちらも非常に小さければ
\begin{align} \sum_if(x_i)\Delta x \simeq \sum_i f(g(t_i))\Delta g(t_i) \end{align}
が成り立つでしょう。ここで$\Delta g(t_i)\equiv g(t_{i+1})-g(t_i)$です。
上の式の右辺を$t$での積分として表すために、
\begin{align} \sum_if(g(t_i))\frac{\Delta g(t_i)}{\Delta t} \Delta t \end{align}
と変形しておきます。あとは$\Delta x \rightarrow 0, \Delta t \rightarrow 0$とすれば
\begin{align} \int f(x)dx =\int f(g(t))\frac{dg(t)}{dt}dt \tag{1} \end{align}
となります。これは置換積分に他なりません。

つまり置換積分は、区分求積の長方形の横の長さのとり方の任意性と解釈できます。

もうすこし違う言葉で言えば、元の座標$x$を違う座標$t$をとったとき（その関係は$x=g(t)$）、$x$で等間隔にわけて長方形の面積を足そうが、$t$で等間隔にわけて足そうが同じ、ということですね。これはつまり、面積を求める際に設定する座標系の任意性を表しています（当然といえば当然です）。

「積分」が座標に依らないことと1形式の積分の関係

以下前章での座標の任意性を多様体論・微分形式の言葉で理解します。

多様体

可微分多様体は、局所的にEuclid空間と同相で、いたるところ座標近傍への同相写像が存在するような空間です。また、座標近傍が重なるところで、その間の座標変換が滑らかです。

多様体それ自体は採用する座標と無関係な性質を持ちます。多様体の何らかの性質の計算には具体的な座標を設定しなければいけないときもあります。しかしどのような座標をもってきても、どれも等価です。多様体の座標近傍として、ユークリッド座標を採ってもいいし、極座標を採ってもいいです。

人は時として、何か「空間」が存在すると、そこに暗黙に座標が存在すると思ってしまいます。多様体にはそのようなアプリオリな座標は存在しません。多様体上の点$p$はあくまで点$p$で、それを何の座標で記述するかは任意です。

ベクトル空間・双対ベクトル空間

ベクトル空間$V$上の1次形式とは、ベクトル空間に相補的・双対な存在です。これはベクトル空間$V$の元に作用して数を返すような写像のことです。このような写像の全体はやはりベクトル空間で、$V$に対し$V^*$などと表し、これを双対ベクトル空間と呼んだりします。

接空間・余接空間・余接バンドル

このような双対を、多様体上の接空間（多様体上のある点$p$での方向微分作用素の空間）に対しても定義できます。多様体${\cal M}$上のある点$p$での接空間を$T_p({\cal M})$とするとき、その双対空間を余接空間と言い、$T^*_p({\cal M})$と書きます。さらに、$T^*_p({\cal M})$を集めた
$$ T^*({\cal M}):=\cup_{p\in {\cal M}}T^*_p({\cal M}) $$
を余接バンドルと言います。

多様体上の1形式

多様体${\cal M}$上の１形式$\omega$とは、${\cal M}$上各点$p$に$T^*_p({\cal M})$の元$\omega_p$をひとつづつ対応させる対応：
$$ \omega: {\cal M}\rightarrow T^*({\cal M}): p \mapsto \omega_p\in T^*_p({\cal M}) $$
です。

いまある接ベクトル$v_p$があったとします。${\cal M}$上の任意の実数値関数$f$の$p$での方向微分は、$p$を通り、$p$での接ベクトルが$v_p$に一致する任意の曲線を$g(t) \ \ (g(0)=p)$として
$$ v_p[f]=\left.\frac{df(g(t))}{dt}\right|_{t=0} $$
です。
（この表式は${\cal M}$の座標のとり方には依存していません。$f$の定義域および$g(t)$の値域は${\cal M}$上の点です。$f\circ g$という写像は、定義域と値域が数で、途中${\cal M}$上の点を経由しています。途中経由しているだけなので、${\cal M}$に具体的に座標を導入する必要はないです）

接ベクトル$v_p$と実数$v_p[f]$との対応を、$T_p({\cal M})$から$\mathbb R$への写像とみなし
$$ (df)_p: T_p({\cal M})\rightarrow {\mathbb R}:v_p \mapsto v_p[f]\in {\mathbb R} $$
とか
$$ (df)_p[v_p]=v_p[f] $$
と表します。これはすなわち、$df_p$は接ベクトル$v_p$に双対であり、$T^*_p({\cal M})$の元だということです。

ここまでは局所座標に依存しない話でしたが、ここで座標を入れます。

ある座標近傍$(U,\phi)$をとります。その上で1形式$\omega$を考えます。
点$Q\in U$で$\omega$のとる値が$\omega_Q=\omega_{iQ}(dq^i)_Q$で表されるとします。
そこで$U$上の各点$Q$で$\omega_{iQ}$の値を取る$U$上の関数$\omega_i$の組、
および各点$Q$でその点の余接空間の基底を与える$m$個の1形式
\begin{align*} dq^i:U\longrightarrow T^*U:Q\mapsto(dq^i)_Q \end{align*}
を考えると、1形式$\omega$は$U$上で
\begin{align*} \omega=\omega_idq^i \end{align*}
と表せます。これが1形式の局所座標表示、$\omega_i$はその成分です。

1形式$\omega$は座標のとり方によりません。よって違う座標近傍により$\bar \omega_j, d\bar q^j$と表示しても
$$ \omega=\omega_idq^i=\bar\omega_jd\bar q^j $$
が成立しています。

線積分

多様体${\cal M}$上の１形式$\omega^1$を考えます。いま、曲線$g(t):I=[a,b]\subset {\mathbb R}$から${\cal M}$への写像があるとします。
この曲線に沿った$\omega ^1$の積分は、$g=q(t)$の接ベクトル場を$\dot g=\dot q^i\partial_i$（ただし$\dot q^i=dq^i/dt$）とすると
$$ \int_g\omega^1:=\int_a^b\langle\omega^1|\dot g\rangle dt=\int^b_a\omega^1_i(g(t))\frac{dq^i}{dt}dt\tag{2} $$
です。これはいわゆる線積分です。

この表式の第１項および第２項は具体的な座標に依存していません。つまり積分が座標に依存しない量であることを物語っています。1形式とベクトル場を$\langle \omega^1|$や$|\dot g\rangle$と表すのも、それが基底に依存しない概念であることを反映しています。この表式はRef.[1]に書かれていますが、量子力学ではおなじみの記法であるDiracのbracket表記は、少なくとも物理プロパーの人間には基底独立性がわかりやすいです。

言いたかったこと

Eq.(1)はEq.(2)と同じ形をしています。これはつまり、Eq.(1)は多様体上ある曲線に沿った1形式の積分＝線積分とみなせるということです。そしてEq.(2)の形にすると、これが具体的な座標のとり方に依存しないことが明確になります。よって、座標変換しても値は変わりません。

このような感じで、ふつう「積分」と呼ぶものを、多様体上の1形式の積分とみなせば、採用する座標に依らないことがわかりやすいですね。

次の２つの見方は同じことを言っています：

１. は関数の積分をする感じ。座標がもともとあって、そこに関数をプロットして積分する。
２. は、先に図形が存在し、その大きさを座標を入れて計算する感じ。

そして2.の視点は、相対論における一般座標変換不変性、ゲージ理論におけるゲージ対称性の考え方の大元になります。

当たり前といえば当たり前のことでした。
ちょっとした覚書でした。

おしまい。