選択公理⇔連結グラフは全域木をもつ

$G=(V,E,\phi)$を連結グラフとする．$\mathcal{T}=\{(V',E',\phi')\mid (V',E',\phi')$は$G$の部分グラフであり，木である$\}$と定める．また，$\mathcal{T}$上の二項関係$\preceq$を部分グラフであることにより定めると，$(\mathcal{T},\preceq)$は半順序集合になる．これが帰納的であることを示す．$\mathcal{C}$を任意の$\mathcal{T}$の鎖とする．$T_0=(\bigcup_{T\in\mathcal{C}}\mathrm{vert}(T),\bigcup_{T\in\mathcal{C}}\mathrm{edge}(T),\phi|_{\bigcup_{T\in\mathcal{C}}\mathrm{edge}(T)})$とおく．任意に$v,v'\in T_0$をとるとき，$\mathcal{C}$が鎖であることからある$(V_1,E_1,\phi_1)\in\mathcal{C}$が存在して$v,v'\in V_1$となる．ゆえに$v$を始点とし$v'$を終点とする道が存在する．また，もし$v$を通るサイクルが存在するとき，そのサイクルを含むような$(V_2,E_2,\phi_2)\in\mathcal{C}$が存在することになり矛盾が生じる．よって$T_0$は連結かつサイクルをもたないことから，木である．よって，$T_0$は$\mathcal{C}$の上界である．したがって，Zornの補題より$\mathcal{T}$は極大元$T$をもつ．もし，$T$が$G$の全域木でないとすると，ある$w,w'\in V$が存在して，$w$を始点とし$w'$を終点とする道は$T$に存在しない．他方$G$は連結であるので，$w$を始点とし$w'$を終点とする道は$G$には存在するので，この道を含むように$T$を拡大したものを$T'$とすれば，これは$T\prec T'$を満たすので，$T$の極大性に反する．よって，$G$の全域木$T$の存在が示された．

$(X_\lambda)_{\lambda\in\Lambda}$を空でない集合からなる族とする．グラフ$G=(V,E,\phi)$を，
$$ \begin{align} V&=\{\bullet\}\cup\{\bigcirc_\lambda\mid\lambda\in\Lambda\}\cup\{\square_\lambda\mid\lambda\in\Lambda\}\cup\Bigl(\bigcup_{\lambda\in\Lambda}(\{\lambda\}\times X_\lambda)\Bigr)\\ E&=\bigcup_{\lambda\in\Lambda}\left(\{a_\lambda\}\cup\{b_{\lambda,x}\mid x\in X_\lambda\}\cup\{c_{\lambda,x}\mid x\in X_\lambda\}\right) \end{align} $$
とし(未定義の文字はすべて異なる)，
$$ \phi(a_\lambda)=\{\bullet,\bigcirc_\lambda\},\;\phi(b_{\lambda,x})=\{\bigcirc_\lambda,(\lambda,x)\},\;\phi(c_{\lambda,x})=\{(\lambda,x),\square_\lambda\} $$
で定める．
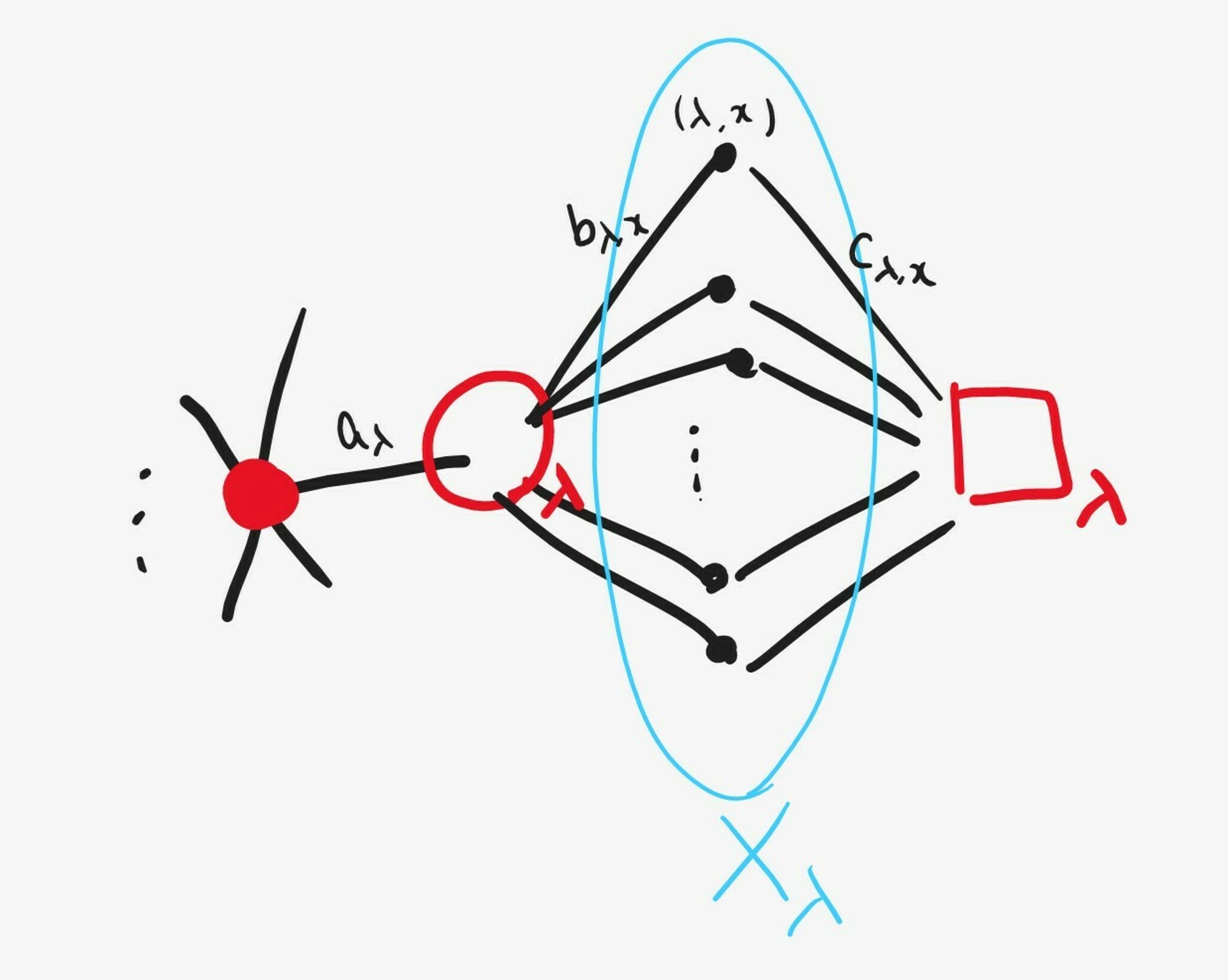Gのイメージ
$G$は連結グラフである．よって全域木$T=(V,E',\phi|_{E'})$が存在する．$T$の連結性より，任意の$\lambda\in\Lambda$に対し$\bigcirc_\lambda$を始点とし$\square_\lambda$が終点となる道が存在し，$T$がサイクルを持たないことからこれは一意に定まる．すなわち，$b_{\lambda,x_\lambda},c_{\lambda,x_\lambda}\in E'$を満たす$x_\lambda\in X_\lambda$が一意に定まる．
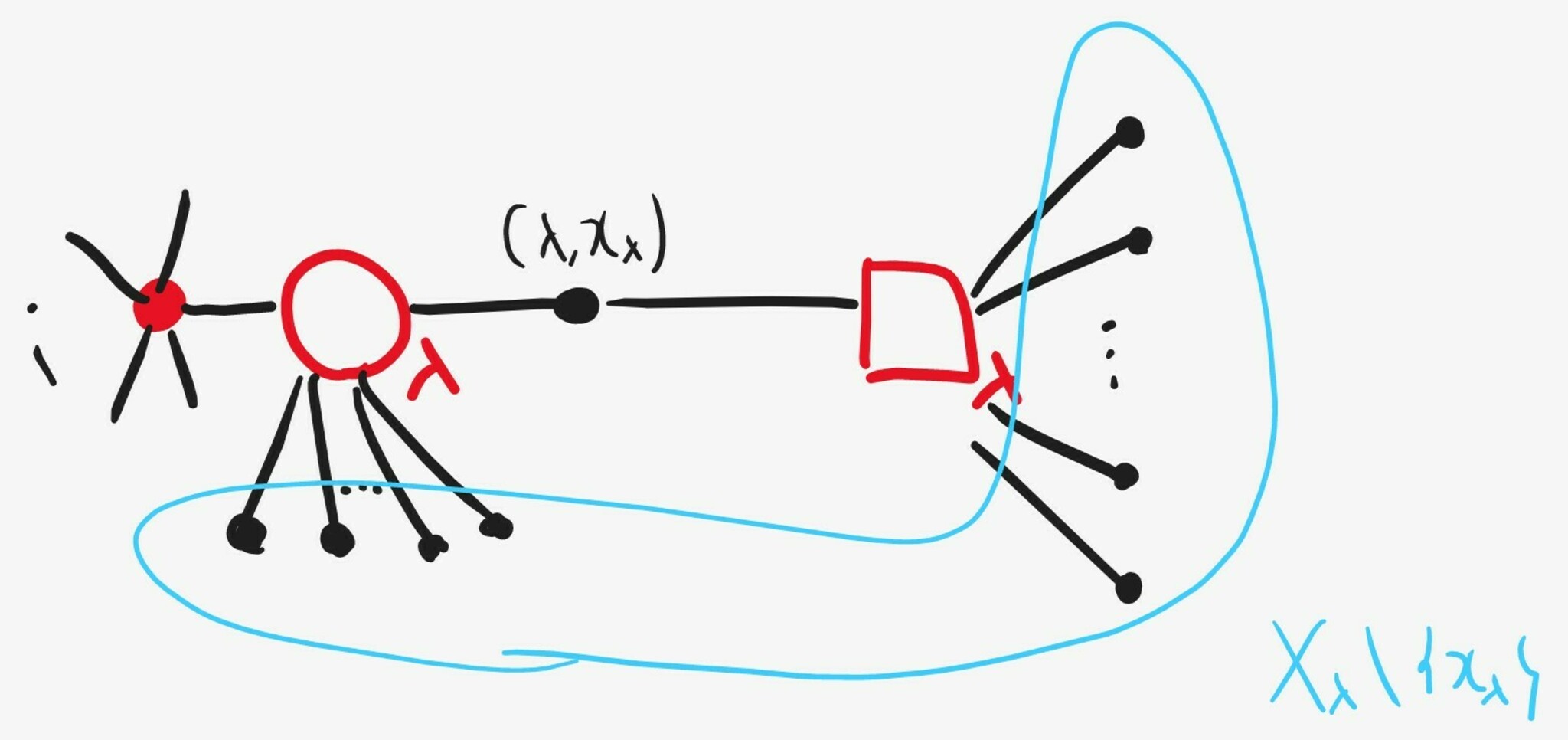Tのイメージ
このとき，$(x_\lambda)_{\lambda\in\Lambda}\in\prod_{\lambda\in\Lambda}X_\lambda$であるから，$\prod_{\lambda\in\Lambda}X_\lambda$は空でない．