JJMO2022本選問4を解こう(複素)
先日行われたジュニア数学オリンピック本選で問4に幾何が配置されたのでこの記事ではこの問題を解説しようと思います.
解答に複素座標を用います.詰まったときはこの記事を参照しましょう(宣伝).
https://mathlog.info/articles/1204
問題
$AB< AC$なる鋭角三角形$ABC$がある.線分$BC$の垂直二等分線と直線$AB,AC$との交点をそれぞれ$D,E$とし,線分$DE$の中点を$M$とする.三角形$ABC$の外接円と直線$AM$が$A$でない点$P$で交わっており,3点$M,A,P$はこの順に並んでいる.このとき,$\angle BPE=90^\circ$が成り立つことを示せ.
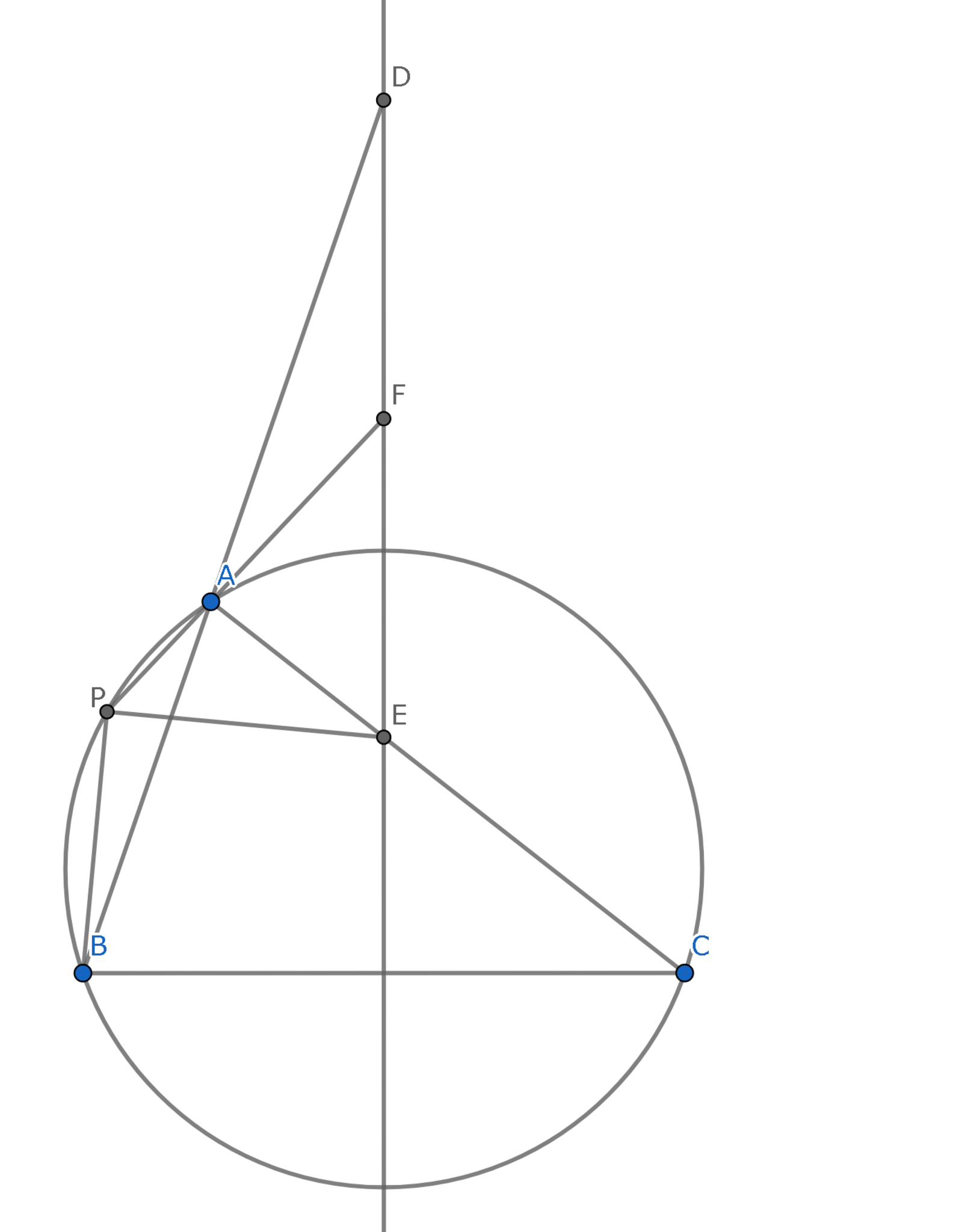 図
図
解説
ある程度複素座標に慣れていれば30分で計算が終わる(どこかでミスをすることを含めても高々60分)と見積もれるでしょう.以下,解答です.※印のところは後で補足,備考を書きます.
三角形$ABC$の外接円の方程式を$|z|=1$とし,$A(1),B(b),C(c)$とする.※1
$AB:z+b\ol{z}=b+1, AC:z+c\ol{z}=c+1$
また,線分$BC$の垂直二等分線の方程式は$z-bc\ol{z}=0$
これら3式より,$D\Big(\dfrac{c(b+1)}{c+1}\Big),E\Big(\dfrac{b(c+1)}{b+1}\Big)$※2なので,$M(m)$とすると,$m=\dfrac{b^2c+bc^2+4bc+b+c}{2(b+1)(c+1)}$である.
ここで,$P$の座標は$A(1),M(m)$より,$\dfrac{1-m}{\ol{m}-1}$である.$1-m$を計算すると,
$1-m=\dfrac{2(b+1)(c+1)-(b^2c+bc^2+4bc+b+c)}{2(b+1)(c+1)}=\dfrac{(bc-1)(b+c+2)}{2(b+1)(c+1)}$
したがって$\ol{m}-1=-\ol{(1-m)}=\dfrac{(bc-1)(2bc+b+c)}{2bc(b+1)(c+1)}$※3
よって,$P$の座標は$\dfrac{bc(b+c+2)}{2bc+b+c}$.
ここで三角形$ABC$の外心について$B$と対称な点を$B^\prime$とする※4と$B^\prime(-b)$なので直線$PB^\prime$の方程式は
$z+\dfrac{bc(b+c+2)}{2bc+b+c}\cdot(-b)\ol{z}=\dfrac{bc(b+c+2)}{2bc+b+c}-b$
すなわち,$PB^\prime:(2bc+b+c)z-b^2c(b+c+2)\ol{z}=b(c+1)(c-b)$
左辺について,$z=\dfrac{b(c+1)}{b+1}$を代入したものを計算すると,
$(2bc+b+c)\cdot\dfrac{b(c+1)}{b+1}-b^2c(b+c+2)\cdot\dfrac{c+1}{c(b+1)}=\dfrac{b(c+1)}{b+1}\Big((2bc+b+c)-b(b+c+2)\Big)=b(c+1)(c-b)$
と,右辺に等しくなるので,$E$は直線$PB^\prime$上にある.
よって$\angle BPE=90^\circ$が示された.$\square$
補足
※1
初めの座標設定ですが,$A$の座標は$1$でなく$a$としても計算量は変わりません.人によっては$a$の方が斉次式のまま計算できて綺麗という人もいるでしょう.
さすがに外接円を$|z|=1$とおかずに進めるのは悪手です.$P$の座標を出すところあたりで詰むと思います.
※2
当たり前といえば当たり前ですが,$D,E$の座標は$b,c$について対称です.
この問題ではこのことによる恩恵が受けられませんが(すぐに$M$の座標計算に使われてしまうので),複素座標が有効な問題は,この「座標の対称性」がありがたいことがしばしばあります.
※3
一般に直線$AP(|a|=1)$と$|z|=1$が再び交わる点の座標が$\dfrac{a-p}{a\ol{p}-1}=-\dfrac{1}{a}\cdot\dfrac{a-p}{\ol{a-p}}$であることを考えると,$\ol{p}$を計算して分子分母を計算して...とするよりは$a-p$を計算してその共役複素数を計算して,とした方が速そうです.
特に今回は$1-m=\dfrac{(bc-1)(b+c+2)}{2(b+1)(c+1)}$と因数分解ができているのでなおさらです.
※4
今回は$P,M,B^\prime$の共線によって題意を示しましたが,最終的なとどめの刺し方は様々です.例えば$E$の座標を$e$として,
・$\dfrac{e-p}{e\ol{p}-1}=-b$を示す(実質的に今回の解答と同じ)
・$\dfrac{p-b}{p-e}$が純虚数であることを示して$\angle BPE=\arg{\dfrac{p-b}{p-e}}=90^\circ$を導く
などが挙げられます.
まとめ
複素はたまにですが難しめの問題に露骨に刺さります.みんなで複素座標勉強しよう!
