極小自由分解
本稿は局所環上の有限生成加群において極小自由分解が存在するならば、複体として一意的であることを示したものである。[1]で証明が委ねられていた部分の行間を補っただけなので誤りを含む可能性が大いにある。
$(A,\mathfrak{m},k)$を局所環,$M$を有限生成$A$加群とする。完全列
$\cdots\rightarrow L_i\overset{d_i}{\rightarrow}L_{i-1}\rightarrow\cdots\rightarrow L_1\overset{d_1}\rightarrow L_0\overset{\varepsilon}{\rightarrow}M\rightarrow0$
が次の3条件を満たすとき、これを$M$の極小自由分解という。
(1)各$L_i$は有限生成自由$A$加群である。
(2)各$i\geq0$に対して$d_iL_i\subseteq\mathfrak{m}L_{i-1}$が成立する。
(3)$\varepsilon\otimes k:L_0\otimes k\rightarrow M\otimes k$は$A$同型写像である。
実は、極小自由分解は存在すれば複体としての同型を除いて一意的であることが示される。その前に「2つの複体が同型」とは何かを述べておく。
$A$を環とする。$A$加群と$A$準同型からなる2つの複体$(K_{\cdot},d),(L_{\cdot},e)$が次の条件を満たすとき、$(K_{\cdot},d)$と$(L_{\cdot},e)$は複体として同型であるという。
(条件)$A$同型の列$\{f_n:K_n\rightarrow L_n\}_{n\in\mathbb{Z}}$が存在して各$n\in\mathbb{Z}$に対して次の図式を可換にする。
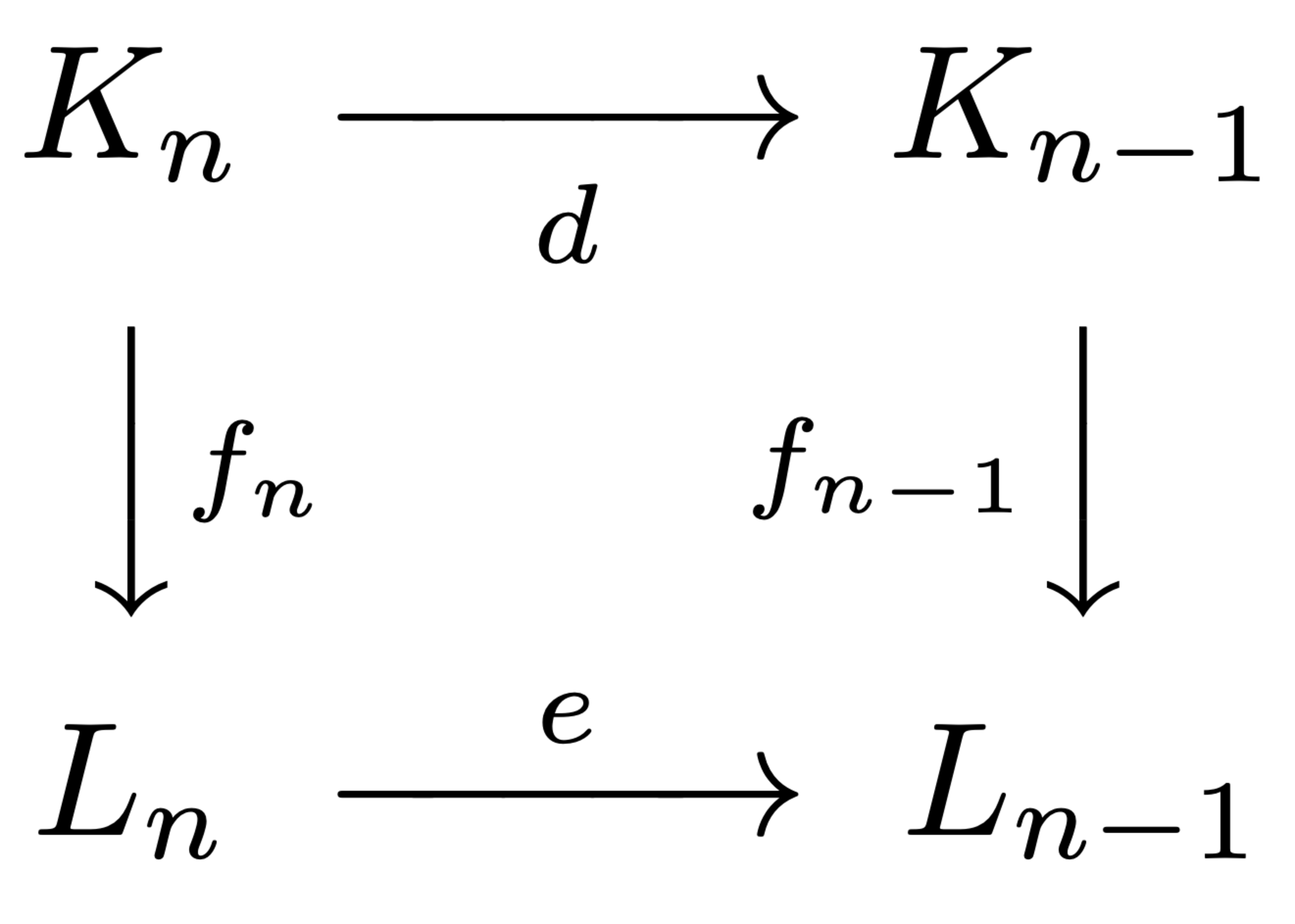
2つの極小自由分解が存在すれば複体として同型であることを示したいが(2)と(3)をうまく使いたいのでそのために補題を用意する。
$(A,\mathfrak{m},k)$を局所環,$M,N$を有限生成$A$加群とする。$A$準同型$\phi:M\rightarrow N$から生じる$k$線型写像$\phi\otimes k:M\otimes k\rightarrow N\otimes k$について次が成立する。
(1)$\phi$は全射で$\ker\phi\subseteq\mathfrak{m}M$が成立する。$\Leftrightarrow$$\phi\otimes k$は$k$同型である。
(2)$M,N$が自由$A$加群ならば
$\phi$は$A$同型である$\Leftrightarrow\phi\otimes k$は$k$同型である。
もう少し良い証明方法があるように思う。(元を取りまくってるので)
$\displaystyle M\otimes k\cong M_{\mathfrak{m}}/\mathfrak{m}M_{\mathfrak{m}}$であることに注意する。このとき、$\phi\otimes k:M_{\mathfrak{m}}/\mathfrak{m}M_{\mathfrak{m}}\rightarrow N_{\mathfrak{m}}/\mathfrak{m}N_{\mathfrak{m}}$は$\displaystyle\frac{a}{b}+\mathfrak{m}M_{\mathfrak{m}}\mapsto\frac{\phi(a)}{b}+\mathfrak{m}N_{\mathfrak{m}}$に対応している。
(1)
($\Rightarrow$)完全列$M\overset{\phi}{\rightarrow}N\rightarrow0$に$-\otimes k$を適用するとtensor積の右完全性から$M\otimes k\overset{\phi\otimes k}{\rightarrow}N\otimes k\rightarrow 0$も完全であることが分かる。よって、$\phi\otimes k$は全射である。$\phi\otimes k$が単射であることが次のように示される。$\displaystyle\frac{x}{s}+\mathfrak{m}M_{\mathfrak{m}}\in M_{\mathfrak{m}}/\mathfrak{m}M_{\mathfrak{m}}$が$\displaystyle(\phi\otimes k)\left(\frac{x}{s}+\mathfrak{m}M_{\mathfrak{m}}\right)=0$を満たしたとする。すると、$\displaystyle\frac{\phi(x)}{s}\in\mathfrak{m}N_{\mathfrak{m}}$ゆえある$m\in\mathfrak{m}$と$n\in N$が存在して$\phi(x)=mn$となる。ここで、$\phi$は全射ゆえ$n=\phi(l)$とすると、$x-ml\in\ker\phi\subseteq\mathfrak{m}M$ゆえ$x\in\mathfrak{m}M$となる。これは$\displaystyle\frac{x}{s}+\mathfrak{m}M_{\mathfrak{m}}=0$を意味するので$\phi\otimes k$は単射である。
($\Leftarrow$)まず、$\ker\phi\subseteq\mathfrak{m}M$を示す。$x\in\ker\phi$を任意の元とする。$\phi(x)=0$ゆえ$(\phi\otimes k)(x\otimes1)=0$である。これは$\displaystyle\frac{x}{1}+\mathfrak{m}M_{\mathfrak{m}}=0$を意味する。よって、ある$a\in A\setminus\mathfrak{m}$が存在して$ax\in\mathfrak{m}M$となるが$A$は局所環であるから$a$は単元ゆえ$x\in\mathfrak{m}M$となり示すべき包含が示される。次に、$\phi$が全射であることを示す。
$\textrm{Coker}\,\phi\otimes k=\textrm{Coker}\,(\phi\otimes k)=0$であるが$A$は局所環ゆえ$\textrm{Coker}\,\phi=0$つまり$\phi$は全射である。([1]の定理4.4を参照せよ。)
(2)$M,N$は自由$A$加群であるから$\phi:M\rightarrow N$は$A$成分の行列で表示される。$M\otimes k,N\otimes k$は自由$k$加群であるから$\phi:M\otimes k\rightarrow \otimes k$は$k$成分の行列で表示される。ここで、$\phi\otimes k=\overline{\phi}$($A$の$k$への像を表す)であることに注意すると
$\phi$は同型$\Leftrightarrow$$\det\phi$は単元$\Leftrightarrow$$\det\phi\in A\setminus\mathfrak{m}$$\Leftrightarrow$$\overline{\det\phi}\neq0$(in$k$)$\Leftrightarrow $$\overline{\phi}$は同型
となり証明が完了する。
$A$を局所環,$M$を有限生成$A$加群,
$\cdots\rightarrow L_i\overset{d_i}{\rightarrow}L_{i-1}\rightarrow\cdots\rightarrow L_1\overset{d_1}\rightarrow L_0\overset{\varepsilon}{\rightarrow}M\rightarrow0,$
$\cdots\rightarrow F_i\overset{e_i}{\rightarrow}F_{i-1}\rightarrow\cdots\rightarrow F_1\overset{e_1}\rightarrow F_0\overset{\delta}{\rightarrow}M\rightarrow0$
を$M$の極小自由分解とする。このとき、上の2つの複体は同型である。
記号の整理のため、$L_{-2}=F_{-2}=0,L_{-1}=F_{-1}=M,d_0=\varepsilon,e_0=\delta$とする。$A$同型の列$\{\,f_n:L_i\rightarrow F_i\}_{i\geq-2}$で各$i\geq0$に対して次の図式を可換にするものが存在することを示せば良い。
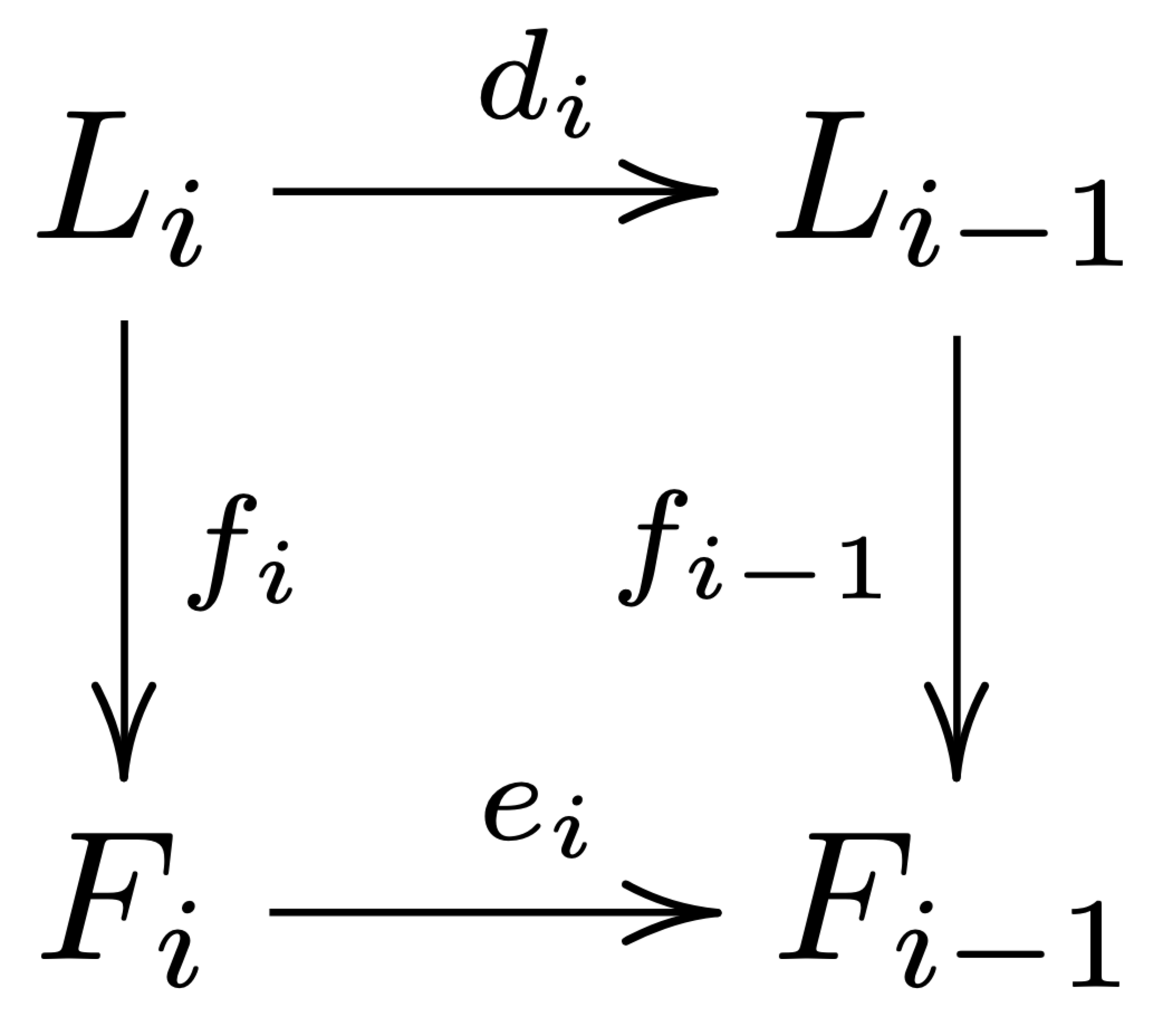 1
1
帰納的に$\{f_n\}_{n\geq-1}$を定義する。まず、$f_{-2}=0,f_{-1}=\textrm{id}_M$として定める。($i=-1$のとき条件を満たすことは明らかである。)$f_{i-1}$まで定まったとして$f_i$を定める。
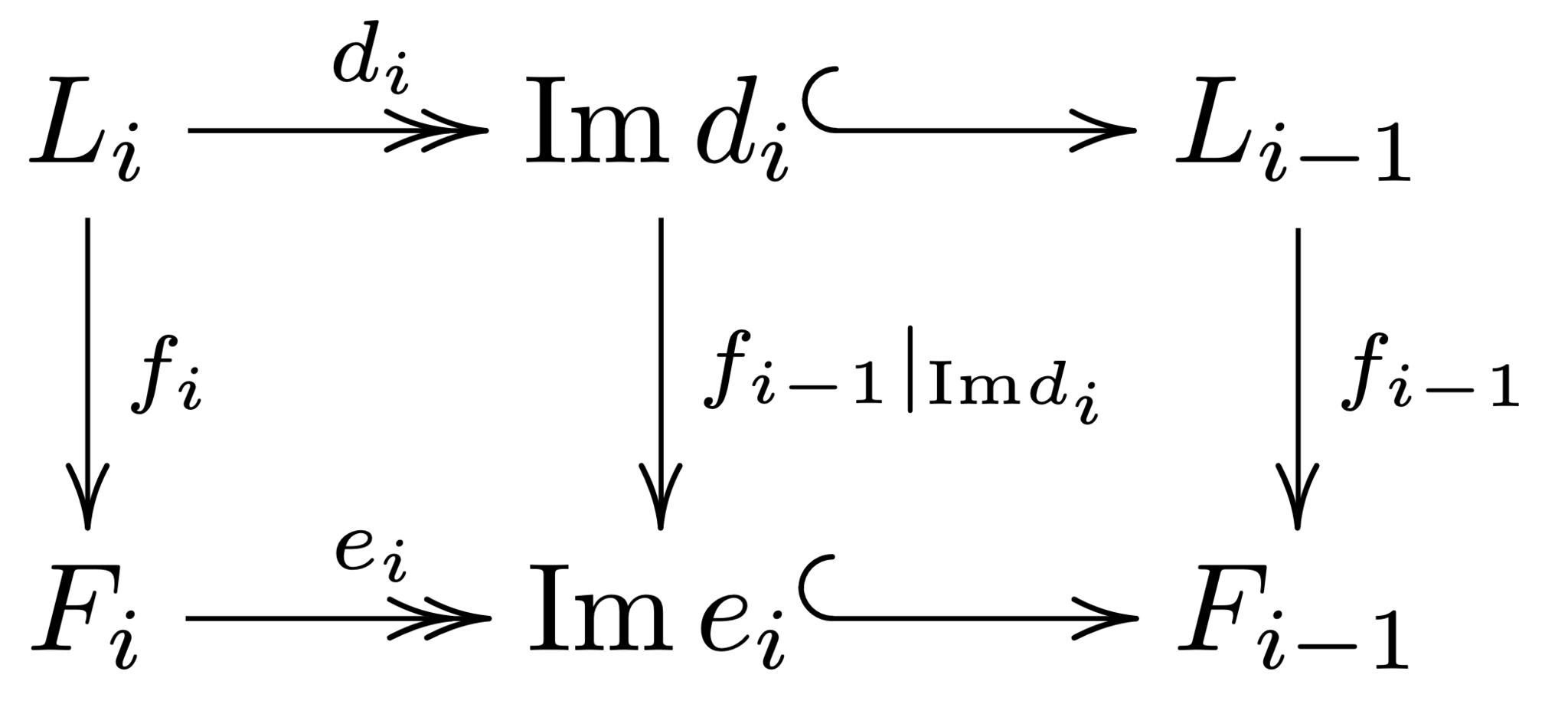
$L_i$は自由加群ゆえ射影加群でもある。$e_i:F_i\rightarrow\textrm{Im}\,e_i$は全射であるから$f_i:L_i\rightarrow F_i$で次の図式の左四角部分が可換にするものが存在する。(真ん中の準同型は右側の準同型を制限したものだから、右側の四角形は可換になる。)
 これ
これ
これを$-\otimes k$することで、次のような可換図式を得る。
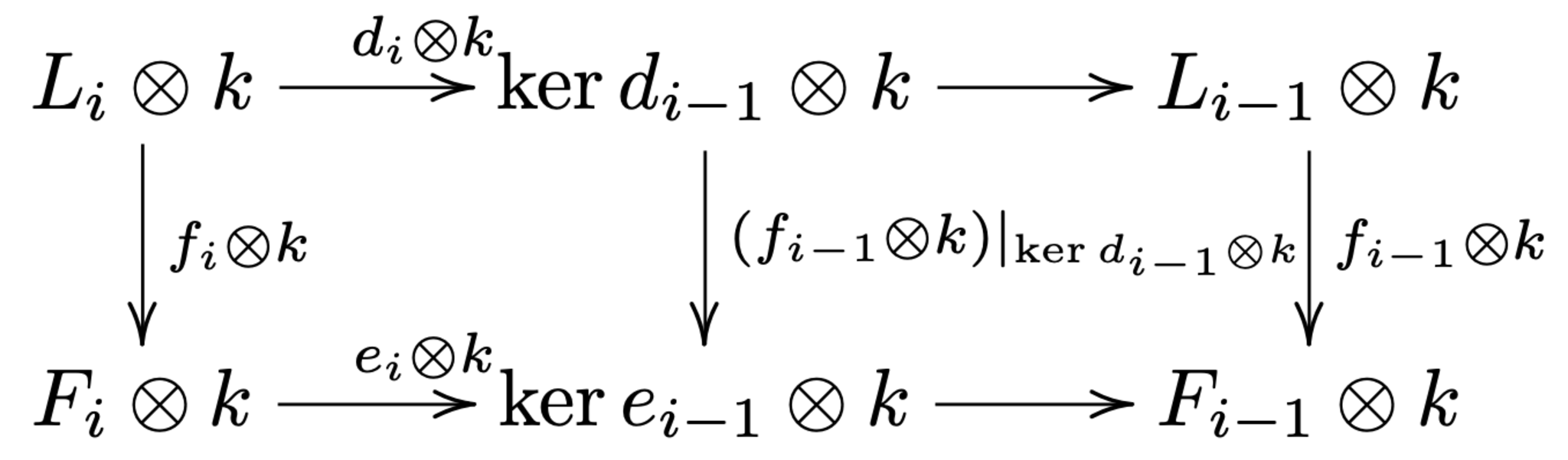
ここで、$(f_{i-1}\otimes k)|_{\ker d_{i-1}\otimes k}=(f_{i-1}|_{\ker d_{i-1}})\otimes k$であることに注意すると次の可換図式から真ん中の準同型は同型になることが分かる。
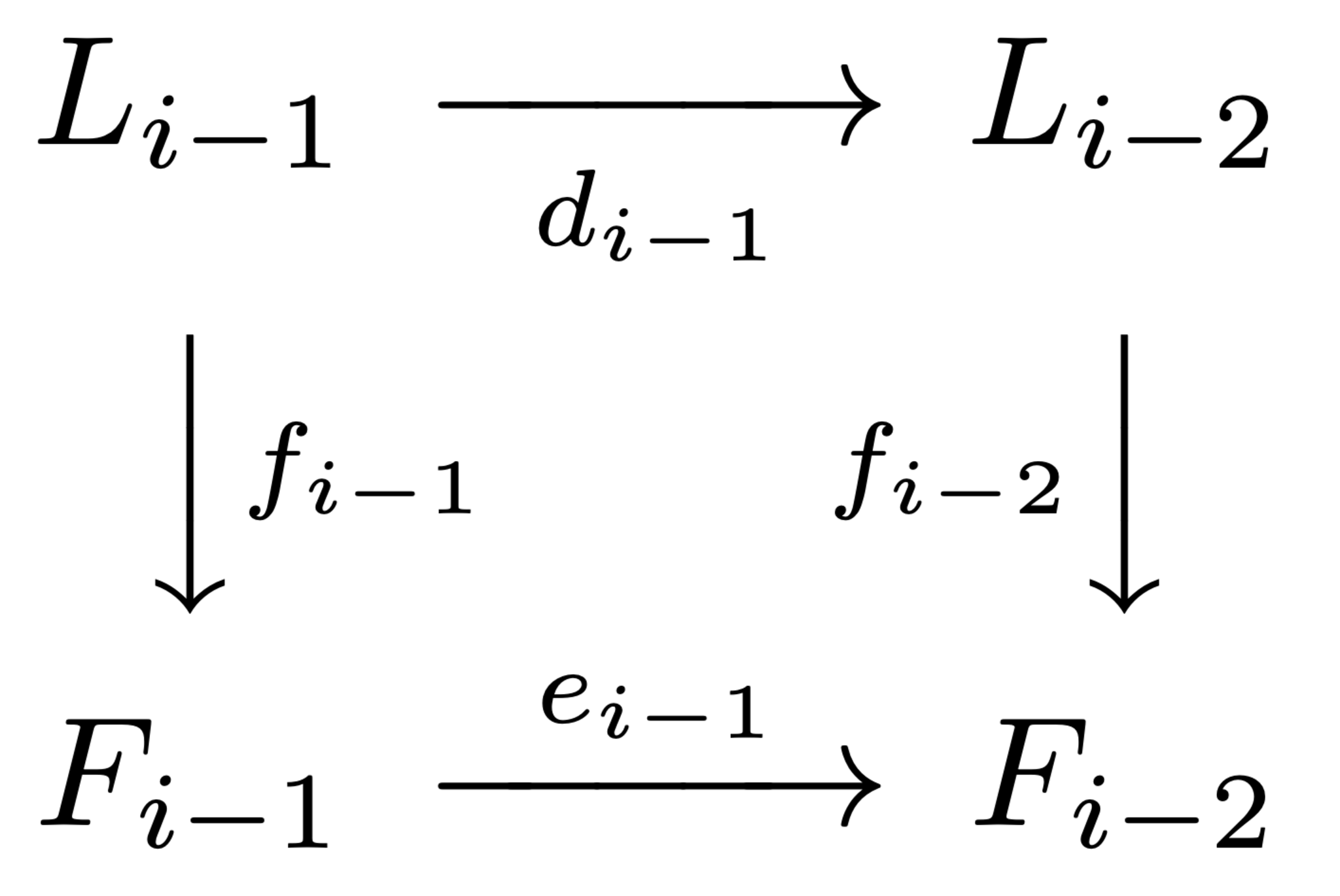
ここで、全射$d_i:L_i\rightarrow\textrm{Im}\,d_i$の核を調べると、極小自由分解の定義から$\ker d_i\subseteq\mathfrak{m}L_i$となるので前補題より$d_i\otimes k$は同型である。同様に、$e_i\otimes k$も同型である。よって、可換性から$f_i\otimes k$も同型であることが分かる。$L_i,F_i$は自由$A$加群であるから前補題より$f_i$も同型であることが分かる。図2を合わせることで図1を可換にする同型$f_i:L_i\rightarrow F_i$が得られるのでこれで証明が完了する。
Noether局所環上では極小自由分解が存在する。
