「くどー問題」の数値計算
はじめに
「くどー」さんが、
そろそろ誰かに解いてほしい自作問題(未解決)
という記事を書かれています。
私には数学的な解決はできないですが、数値計算ならできると思い、やってみました。
問題の定義等は上記記事を御覧ください。
現状は
- $n=3$から$500$まで数値計算で調べた
- $n=3,6$では、上記記事にあるように、条件を満たす取り除き方が存在することを確かめた
- $n=3, 6, 119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$以外の$500$以下の自然数には、条件を満たす取り除き方は存在しないことを確かめた。
$n=119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$では、計算量が多いため探索が完了していない。
というかんじです。
つまり
- いまのところ$n=3,6$以外で条件を満たす取り除き方は見つかっていない
- $n=4,5$および$7\le n\le 118$には条件を満たす取り除き方は存在しない
以下少し詳しく説明します。
なお、整数論の問題ながら、整数論的な考察は一切ありません。ご容赦ください。
定義
このあと出てくる用語・記号に関し定義をします。
（先にくどーさんの記事をみておいたほうがよいと思います。また、当方数学に不慣れなので、以下の定義に不備があったらすみません。その場合フィーリングで理解してください）
「くどー条件」の定義：
自然数の集合$\{a\}$が
$(\sum_ia_i^3)\equiv 0 \ \ \ \ \ \left( {\rm mod} \ \ (\sum_ia_i) \right)$
を満たすとき、「$\{a\}$はくどー条件を満たす」という。$1$から$n$までの自然数の集合$\{1,2,\ldots,n\}$から、$b^{(i)}_k$を自然数として($2\le b^{(i)}_k\le n-1, \ 1\le k\le m, \ b^{(i)}_k\neq b^{(i)}_l$ for $k\neq l$)
$$ b^{(i)}_1\rightarrow b^{(i)}_2\rightarrow\ldots \rightarrow b^{(i)}_m $$
の順に数字を取り除く。どの削除の段階でも、その集合がくどー条件を満たすとき
${\rm DelList}^{(i)}(m;n):=[b^{(i)}_1,b^{(i)}_2,\ldots,b^{(i)}_m]$を「可能な削除列」と呼ぶ。
$i$は、そのような列（一般には複数存在します）につけたラベルであり、これは（それが存在するなら）$1$から$L(m;n)$までの値を取るものとする。
$L(m;n)=0$とは、この$m,n$に対し可能な削除列が存在しないことを表す。$L(n-2;n)>0$を満たす$n$を「削除可能な$n$」とよぶ
ある$n$に対して、$L(m;n)>0$となる$m \ (\le n-2)$の最大値を$m_{\rm max}^{(n)}$とする。このとき、$m_{\rm max}^{(n)}=n-2$を満たす$n$は、削除可能な$n$と同値。
以上の準備のもと、くどーさんの作成した問題は
削除可能な$n$は無限に存在するか？
と言えます。
数値計算でわかったこと
冒頭の繰り返しになりますが、数値計算でわかっていることを書いておきます。
- $n=3,6$は、くどーさんの記事にもあるように、削除可能です。
- 500以下の自然数で、$3, 6, 119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$以外の$n$は削除不可能です。
- $n=119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$が削除可能か否かはわかりません。
これらの$n$では、可能な削除列${\rm DelList}^{(i)}(m;n)$を$m$が小さいところから構成していく過程で、ある$m$から非常に多くの可能な削除列が存在するようになり、数値計算に時間がかかって探索が終わりませんでした。
ちなみに、$\{1,n\}$に数字を付け足していき、各段階でその集合がくどー条件を満たすかを確認していくことでも、可能な削除列を作ることができます。が、この「逆探索」は、上記の「順探索」より、可能な削除列が途中で多くなり、効率的ではありませんでした。
Appendix (a)に、数値計算のコードおよびアルゴリズムの概要を簡単に示しておきましたので、よろしければ御参照ください。
可能な削除列の特長
可能な削除列を具体的に見てみると、特長があることがわかります。
Appendix (b)に可能な削除列の例が載っていますのでご参照ください。
例えば$n=6$を見てみます。これは削除可能です。${\rm DelList}(m=4;n=6)$は1つだけ存在し、それは
$$
[3,4,5,2]
$$
です。3,4,5と連続した自然数が見られます。
このような「連続する自然数」は、多くの$n$で見られます。
Appendix (b)を見ると
- n=19では、${\rm DelList}$は15の後4,5,6,...と続く
- n=54では33の後7,8,9,...と続く
- n=59では30,29の後10,11,12,...と続く
- n=63では56,40の後9,10,11,...と続く
- n=74では37の後8,9,10,...と続く
- n=119では60の後10,11,12,...と続く（探索は終わってないが）
という特長があることがわかります。
理由はよくわかりません。
$m_{\rm max}^{(n)}$のグラフ
$m^{(n)}_{\rm max}$を、$n$に対してプロットすると以下の図１のようになります：
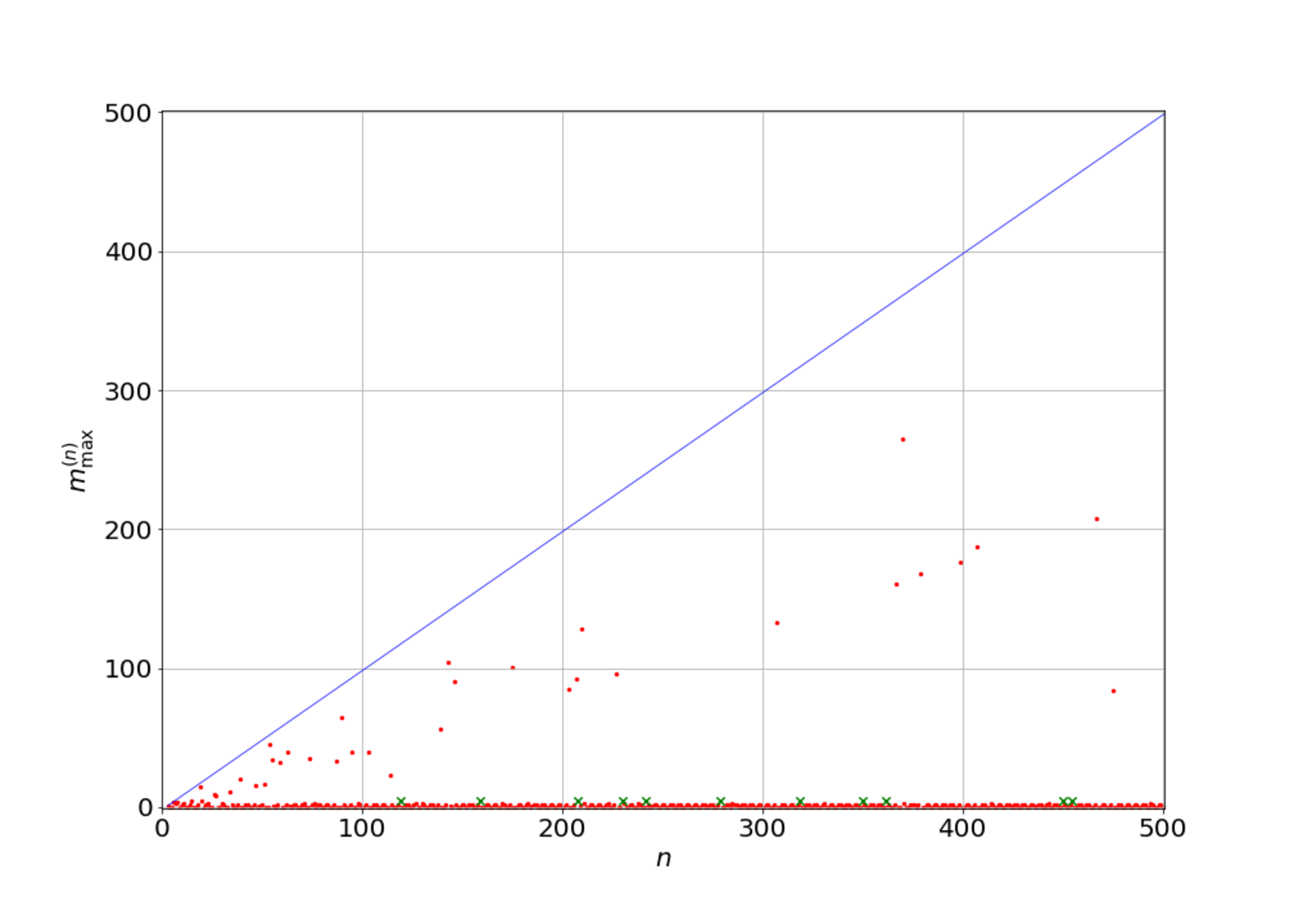m^{(n)}{\rm max}をnに対してプロットした図。青い線はm^{(n)}{\rm max}=n-2の線。緑のバツが存在するnでは、探索が終わっていないため、データは存在しない。
青い線は$m_{\rm max}^{(n)}=n-2$のグラフです。これに$m^{(n)}_{\rm max}$が乗れば、その$n$は削除可能です。よって、$n=3,6$では$m_{\rm max}^{(n)}$は青い線に乗っています（見えませんけど）。逆に言えば、それ以外の点で青い線に乗っているものはありません。緑のバツのついた$n$では探索が終わっていません。
多くの場合、$m_{\rm max}^{(n)}$は0から3程度の値をとります。ときに$m_{\rm max}^{(n)}$が大きくなる$n$があります。しかし、それらにはっきりとした傾向は見られないように思います。なんとなーく、$m^{(n)}_{\rm max}=n/2$の付近にデータが集まっているような気もしますが、よくはわかりません。
各$n$に対する$L(m;n)$
$m^{(n)}_{\rm max}$がある程度大きくなる$n: 19, 54, 55, 59, 63, 74$に関し（適当に選んでいます）、$m$を横軸にして削除列の数$L(m;n)$をプロットしたものを図２に示します：
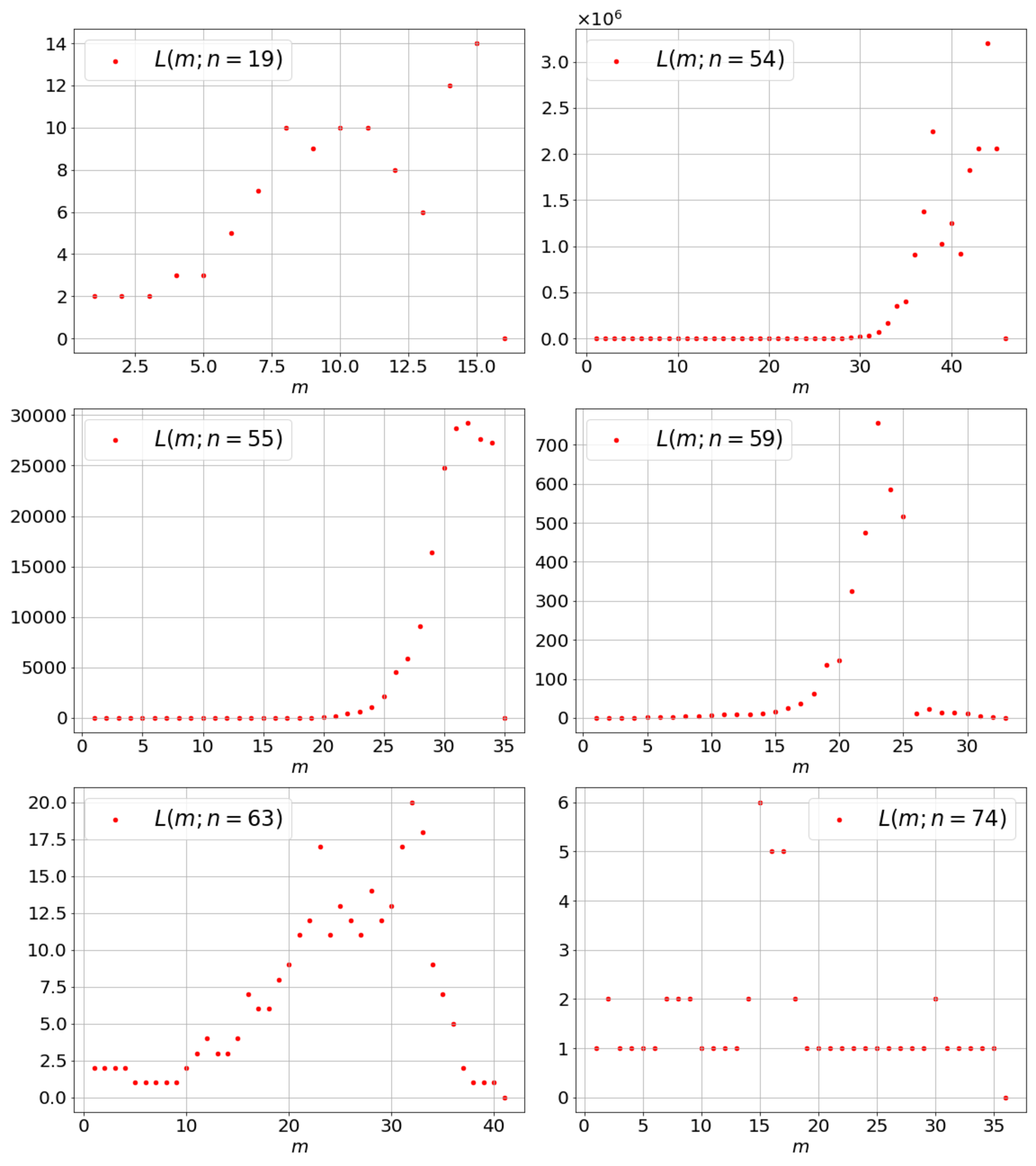n=19, 54, 55, 59, 63, 74におけるL(n;m)。縦軸のスケールがnにより違うことに注意
縦軸のスケールが図によって大きく異なることに注意してください。特に$n=54$の図の縦軸は、$10^6$がかかっています。各図のいちばん右端の$L(m;n)$の値は0で、これ以上の$m$ではすべて$L(m;n)=0$です。
$n=19, 63, 74$では$L$は全体に小さい値(〜${\cal O}(1)$)で推移し、ゼロになります。$n=54, 55, 59$では、$L$は$m$が小さいとき${\cal O}(1)$で、ある$m$で急激に$L$が大きくなります。計算が完了していない$n$($=119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$)では、このように急激に$L$が大きくなるため、計算量が大きくなります。計算は終わりましたが、$n=54$も同様の傾向を持ち、計算量が大きいです。
更に図2を対数プロットにしたのが図3です：
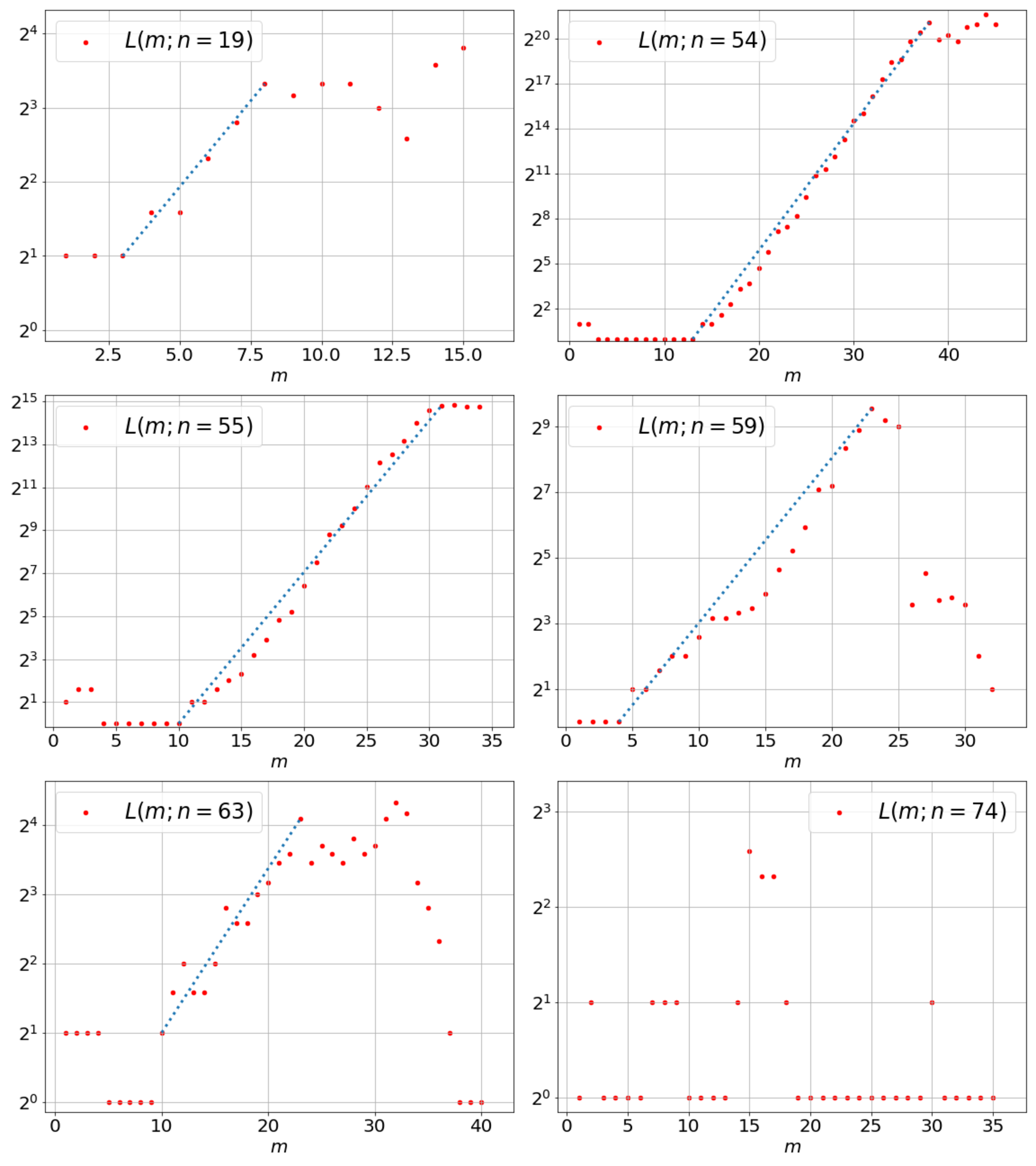図２を対数プロットしたもの。青い点線は、線形領域をy=aexp(bm)で近似した線。
これを見ると、$n=74$以外、線形に近い領域が存在するように思えます。これはつまり、$L$が$m$に対してexponentialで増加する領域が存在するということです。青い点線は、線形領域を$L(m;n)=a_n\exp(b_n m)$で近似した線です（ある2点を通るように$a_n,b_n$を求めています。フィットではありません）。このときexponent $b_n$は
- $n=19$: $b_{19}\sim 0.32$
- $n=54$: $b_{54}\sim 0.59$
- $n=55$: $b_{55}\sim 0.49$
- $n=59$: $b_{59}\sim 0.35$
- $n=63$: $b_{63}\sim 0.39$
となります。
これが意味するのは、$m_{\rm max}^{(n)}$が大きい$n$では、この中間的な$m$の領域で
$L(m+1;n)/L(m;n)$がだいたい$\exp(b)$くらい。そしてそれはおおよそ一定
ということです。そして$\exp(b)$は1.4から1.8くらいになっています。これはつまり、この$m$の領域で
ある$m$における可能な削除列に、数字を付け加え$m+1$における可能な削除列を作る際、付け加えることのできる数字は、平均して、1つより多く2つより少ない
ということです。付け加えられる数字は「少ない」と言えるかと思います。
確率的な探索
計算量が多くなり計算が終わらない$n$に対し、計算が終わった$\{L(m;n)\}$から、全探索ではなく確率的に適当に$L(m;n)$を選び出し、それらのみ探索していくということもやってみました。運がよければ、長さが$n-2$の可能な削除列を見つけることができるかもしれないと思ったのですが、これはことごとく失敗しました。
まとめ
とりあえずわかっていることは以上です。
改めてまとめておくと
- $n=3$から$500$まで数値計算を行い、削除可能か確かめた
- $n=3,6$は（くどーさんの記事にあるように）削除可能
- $n=3, 6, 119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$以外の$500$以下の自然数は削除不可能。
$n=119, 159, 208, 230, 242, 279, 319, 350, 362, 450, 455$では、計算量が多いため探索が完了していない。 - 多くの$n$において、$m^{(n)}_{\rm max}$は$0$から$3$程度である
- 可能な削除列には、連続した自然数が小さい方から並ぶ傾向がある
- $m$が小さいとき、$L(m;n)$は"${\cal O(1)}$"。大抵の場合"${\cal O(1)}$"のままゼロになる。しかし、稀に、ある$m$から$L(m;n)$が急激に大きくなる$n$が存在する（計算が完了していない$n$がこれにあたる）。増加は指数関数的であることが多く、$L(m+1;n)/L(m;n)$はおおよそ1.4から1.8程度
という感じです。
おしまい${}_\blacksquare$
Appendix
Appendix (a): 数値計算の概要
数値計算は以下のようなアルゴリズムで行っています：
$\{1,2,\ldots,n\}$に対し可能な削除列の集合$\{{\rm DelList}^{(i)}(m;n)\}_{i=1,\ldots,L(m;n)}$が与えられた時、この可能な削除列それぞれに対し数字を列の最も右に1つ加えて$\{{\rm DelList}^{(i)}(m+1;n)\}_{i=1,\ldots,L(m+1;n)}$をつくり、それぞれの列が可能かチェックする。これを$m=0$から再帰的に行うことで（$m=0$では可能な削除列は空）、$m=n-2$において可能な削除列が存在するか調べる。
以下に使用したPythonコードを載せておきます。実行環境は"Google Colaboratory"と"Amazon SageMaker Studio Lab"です。
C的な言語とかFortranとか、またはGPUで計算したらもっと速いと思います。
コード中の変数と、本記事のnotationとの対応は以下です：
\begin{align} {\rm Nuplim} &\leftrightarrow n \\ {\rm Nm} &\leftrightarrow m \\ {\rm Nlist} & \leftrightarrow \{1,2,\ldots,n\}\\ {\rm rem\_list} &\leftrightarrow \{{\rm DelList} (m;n)\}\\ {\rm pos\_list} &\leftrightarrow 「\{1,2,\ldots,n\}から{\rm DelList}^{(i)} (m;n)を削除した自然数の集合」の集合 \end{align}
インプットはNuplim($=n$)とNthreadです。Nthreadは並列計算のスレッド数です。実行環境に合わせて好きな値を入れてください。もっとも、大抵の$n$では並列にする必要はありません。
from concurrent import futures
import numpy as np
import pickle
import sys
#---------
def Kudo_prob_01(Nuplim):
Nlist = [i+1 for i in range(Nuplim)]
temp_list = []
temp_pos_list = []
temp_rem_list = []
for i in range(1,Nuplim-1):
temp_list[:] = Nlist[:]
temp_list.pop(i)
if np.array([j**3 for j in temp_list]).sum() % np.array([j for j in temp_list]).sum() == 0:
temp_pos_list.append(temp_list[:])
temp_rem_list.append([Nlist[i]])
return temp_pos_list,temp_rem_list
def Kudo_prob_gt01(Nuplim,Nm,pos_list,rem_list):
if pos_list == []:
Nlen_pos_list = 2
else:
Nlen_pos_list = len(pos_list[0])
temp_list=[]
temp_pos_list=[]
temp_rem_list=[]
for k,i_list in enumerate(pos_list):
for i in range(1,Nlen_pos_list-1):
temp_list[:] = i_list[:]
temp_list.pop(i)
if np.array([j**3 for j in temp_list]).sum() % np.array([j for j in temp_list]).sum() == 0:
temp_pos_list.append(temp_list[:])
temp_rem_list.append(rem_list[k]+[i_list[i]])
return temp_pos_list,temp_rem_list
#---------
# Main:
## inputs ###
Nuplim = 10
Nthread = 10
#############
print ("#############")
print ("n =",Nuplim)
print ("### start ###")
# calculation 01:
pos_list, rem_list = Kudo_prob_01(Nuplim)
print ("- m =",1)
print ("L(n;m) =",len(rem_list))
for Nm in range(1,Nuplim-2):
print ("- m =",Nm+1)
length_datafile = len(pos_list)
Nconf = int(length_datafile/Nthread)
Nres = length_datafile-Nconf*Nthread
# print ("length_datafile,Nconf,Nres,tot:",length_datafile,Nconf,Nres,Nconf*Nthread+Nres)
pos_list_div = []
rem_list_div = []
for i in range(Nthread-1):
pos_list_div.append(pos_list[Nconf*i:Nconf*(i+1)])
rem_list_div.append(rem_list[Nconf*i:Nconf*(i+1)])
ilast = Nthread-1
pos_list_div.append(pos_list[Nconf*ilast:])
rem_list_div.append(rem_list[Nconf*ilast:])
# calculation greater than 01:
future_list = []
with futures.ThreadPoolExecutor(max_workers=Nthread) as executor:
for i in range(Nthread):
future = executor.submit(Kudo_prob_gt01,Nuplim,Nm,pos_list_div[i],rem_list_div[i])
future_list.append(future)
pos_list = []
rem_list = []
for x in future_list:
if x.result()[0] != []:
#print ("x.result():",x.result())
pos_list = pos_list + x.result()[0]
rem_list = rem_list + x.result()[1]
print ("L(n;m) =",len(rem_list))
print ("### finished ###")
if len(rem_list) > 0:
print ("n =",Nuplim, " is deletable !!!!!!!!!!")
else:
print ("n =",Nuplim, " is undeletable")
print ("")
Appendix (b): 可能な削除列の具体例
${\rm DelList(m;n)}$の具体例をいくつか示します。$n, m, L(m;n)$の後、四角括弧でくくった数列で、可能な削除列（の一部）を示しています。
- n=6
m=4
L(m;n)=1
[3,4,5,2]
- n=19
m=15
L(m;n)=14
[15, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 2, 18]
[15, 4, 5, 6, 7, 8, 9, 16, 18, 12, 3, 17, 10, 11, 13]
[15, 4, 5, 6, 7, 8, 9, 16, 18, 12, 3, 17, 10, 11, 14]
[15, 4, 5, 6, 7, 8, 9, 16, 18, 12, 3, 17, 10, 14, 11]
[15, 4, 5, 6, 7, 8, 9, 16, 18, 12, 10, 17, 3, 11, 13]
[15, 4, 5, 6, 7, 8, 9, 16, 18, 12, 10, 17, 3, 11, 14]
[15, 4, 5, 6, 7, 8, 9, 16, 18, 12, 10, 17, 3, 14, 11]
[15, 4, 5, 6, 7, 9, 8, 10, 11, 12, 13, 14, 16, 2, 18]
[15, 4, 5, 6, 7, 9, 8, 16, 18, 12, 3, 17, 10, 11, 13]
[15, 4, 5, 6, 7, 9, 8, 16, 18, 12, 3, 17, 10, 11, 14]
[15, 4, 5, 6, 7, 9, 8, 16, 18, 12, 3, 17, 10, 14, 11]
[15, 4, 5, 6, 7, 9, 8, 16, 18, 12, 10, 17, 3, 11, 13]
[15, 4, 5, 6, 7, 9, 8, 16, 18, 12, 10, 17, 3, 11, 14]
[15, 4, 5, 6, 7, 9, 8, 16, 18, 12, 10, 17, 3, 14, 11]
- n=54
m=28
L(m;n)=4573
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 38, 25, 26, 27, 28, 29, 30, 31, 32, 49]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 53]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 53, 32]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 53, 49]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 53, 52]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 53, 31, 32]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 53, 31, 49]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 53, 31, 52]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 53, 52, 31]
[33, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 42, 20, 40, 22, 23, 24, 25, 26, 27, 28, 29, 30, 53, 52, 51]
...
- n=55
m=22
L(m;n)=451
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 40, 24, 25, 26, 27]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 40, 24, 38, 26, 27]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 40, 24, 38, 26, 36]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 26, 54, 40]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 26, 54, 53]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 54, 26, 40]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 54, 26, 53]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 54, 53, 26]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 54, 53, 39]
[28, 7, 8, 9, 10, 11, 12, 13, 14, 15, 27, 36, 41, 34, 21, 22, 23, 24, 25, 54, 53, 52]
...
- n=59
m: 21
L(m;n)=326
[30, 29, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28]
[30, 29, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 53]
[30, 29, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 27, 26, 28]
[30, 29, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 27, 26, 53]
[30, 29, 10, 11, 52, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28]
[30, 29, 10, 11, 52, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 38]
[30, 29, 10, 11, 52, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 32, 58, 57, 56, 55]
[30, 29, 10, 11, 52, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 54, 42, 57, 55, 44]
[30, 29, 10, 11, 52, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 54, 42, 57, 55, 56]
[30, 29, 10, 11, 52, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 54, 42, 57, 56, 43]
...
- n=63
m=33
L(m;n)=18
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 46, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 46, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 44, 54]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 46, 26, 44, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 27, 54]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 46, 26, 44, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 46, 26, 44, 28, 42, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 52, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 4]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 52, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 52, 18, 50, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 2, 4, 6, 8]
[56, 40, 9, 10, 11, 12, 13, 14, 15, 16, 52, 18, 50, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 2, 4, 6, 39]
...
- n=74
m: 30
L(m;n)=2
[37, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36]
[37, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 56]
- n=119
m=51
L(m;n)=161747
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 94]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 40]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 92, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 92, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 118]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 92, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 118, 58]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 92, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 118, 117]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 92, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 118, 57, 58]
[60, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 94, 41, 92, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 118, 57, 117]
...
この記事を高評価した人
この記事に送られたバッジ
投稿者
