カタラン数とその拡張 その1 〜カタラン数の意味と一般項〜
カタラン数とは次の一般項で定義される数列で,組合せ論において様々な意味を持ちます
カタラン数とは,次の一般項で定義される数列
$$c_n=\frac{1}{n+1}{_{2n}}C_n$$
これから3回にわたって,カタラン数とその一般化を考えていきます.
次のようなテーマで紹介していこうと考えています.
その1. カタラン数の意味と一般項
その2. 最短経路を通したカタラン数の拡張
その3. 標準ヤング盤を通したカタラン数の拡張
組合せ論における意味
まずは,組合せ論においてカタラン数が現れる例を挙げていきます.
一般項の証明は最後に行うので,まずはこれらの命題の同値性を確認していきましょう.
$xy$平面上で,$(0,0)$と$(n,n)$を向かい合う頂点とする正方形状の格子を考える.
この格子上における$(0,0)$から$(n,n)$への最短経路で,常に領域$x\geq y$を通るものの総数は,$c_n$に等しい
$n$個の$A$と$n$個の$B$を並べてできる順列であって,任意の$1 \leq i \leq2n$に対して,
($i$番目までの$A$の個数)$\geq$($i$番目までの$B$の個数)
が成り立つものの総数は$c_n$に等しい
ちなみに,$A$を"(",$B$を")"に置き換えれば,命題2の条件は$n$組の()が正しく並べられる条件に一致します.すなわち$n$組の括弧を正しく並べる方法の総数はカタラン数ということです.
この順列において,$A$を$x$軸方向$+1$の移動,$B$を$y$軸方向$+1$の移動に対応させると,これは$(0,0)$から$(n,n)$への最短経路で,常に領域$x\geq y$を通るものの総数に等しい.よって,命題2$ \Longleftrightarrow$命題1が成立する.
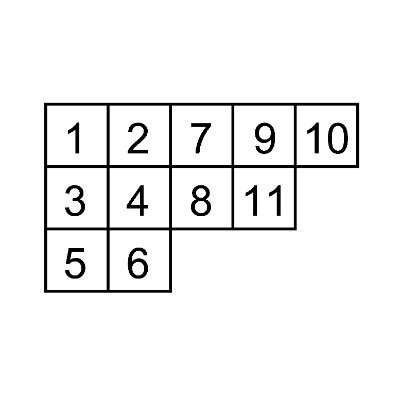
$2\times n$のマス目に$1$から$2n$までの数字を1つずつ書き込むとき,次の条件を満たす方法の総数は,$c_n$に等しい
- 横に隣り合う任意の2つのマスについて,左に書かれた数字よりも右に書かれた数字の方が大きい.
- 縦に隣り合う任意の2つのマスについて,上に書かれた数字よりも下に書かれた数字の方が大きい.
$i=1,2,3,\cdots,2n$を順番に書き込んでいくと考え,下に数字を書き込むことを$A$,上に数字を書き込むことを$B$として表すことでできる順列を考える.このとき,条件を満たすマスは,$n$個の$A$と$n$個の$B$を並べてできる順列であって,任意の$1 \leq i \leq2n$に対して,
($i$番目までの$A$の個数)$\geq$($i$番目までの$B$の個数)
が成り立つものと1対1に対応する.よって,命題3$ \Longleftrightarrow$命題2が成立する.
命題1からすぐに同値性が分かるのはここまでです.カタラン数に対して成り立つ漸化式を考えてみると,さらに世界が広がります.
カタラン数$c_n$について,次の漸化式が成立する.
$$
c_0=1, c_{n+1}=\sum_{k=0}^{n}c_k c_{n-k}
$$
$c_0=1$は明らか.命題1における最短経路で,最初に通った$y=x$上の点を
$(k+1,k+1)$とする.$k$を固定して考えた時,命題1を満たす最短経路の総数は,
($(1,0)$から$(k+1,k)$の最短経路で,常に領域$x\geq y+1$を通る方法の総数)
$\times $($(k+1,k+1)$から$(n,n)$の最短経路で,常に領域$x\geq y$を通る方法の総数)
であるから,$c_k c_{n-k-1}$となる.
よって,これを$k=0,1,2,3,\cdots,n-1$について足し合わせて
$$c_{n}=\sum_{k=0}^{n-1}c_k c_{n-1-k}$$
よって
$$c_{n+1}=\sum_{k=0}^{n}c_k c_{n-k}$$
逆に,$c_n$がこの漸化式を満たす時,命題1は成り立つ.
頂点を区別できる凸$n+2$角形を,交差しない$n-1$本の対角線で$n$個の三角形に分割する方法の総数は$c_n$である.
$n=1$のとき1通りであって,$c_1=c_0c_0=1$であるから成立.
与えられた凸$n+2$角形の頂点を順に$P_0,P_1,\cdots,P_{n+1}$とする.
このとき,$P_{n}P_{n+1}P_k$が1つの三角形となる$k (0\le k\le n-1)$がただ1つ存在する.$k$を固定した時,分割の総数は
($k+2$角形$P_{n+1}P_0P_1P_2\cdots P_{k}$の分割の総数)$\times $($n-k+1$角形$P_k P_{k+1}P_{k+2}\cdots P_n$の分割の総数)
であるから,$c_k c_{n-k-1}$となる.これを$k=0,1,2,3,\cdots,n-1$について足し合わせて
$$c_{n}=\sum_{k=0}^{n-1}c_k c_{n-k-1}$$
よって
$$c_{n+1}=\sum_{k=0}^{n}c_k c_{n-k}$$
逆に,$c_n$がこの漸化式を満たす時,命題5は成り立つ.
一般項の証明
さていよいよ一般項を導いていきます.3通りの証明を紹介します.
一番簡潔で良く知られている証明は次の証明です.
命題1を示す.
$(0,0)$から$(n,n)$までのすべての最短経路から,$y>x$を通る経路の総数を引くと考える.
$y>x$を通る経路$\lambda$において,最初に通る直線$y=x+1$上の点を$P$とする.
$\lambda$における$(0,0)$から$P$までの経路と,
$\lambda$における$P$から$\lambda$までの経路を$y=x+1$に対して対称移動させてできる経路を
つなげてできる経路$\lambda'$を考える.
このとき,$\lambda'$には$(0,0)$から$(n-1,n+1)$までの最短経路がちょうど1つずつ現れる.よって,$y>x$を通る経路の総数は${_{2n}}C_{n-1}$に等しい
すべての最短経路は${_{2n}}C_n$個あるから,条件をみたす最短経路の総数は
$${_{2n}}C_n-{_{2n}}C_{n-1}={_{2n}}C_n-\frac{(2n)!}{(n-1)!(n+1)!}={_{2n}}C_n-\frac{n}{n+1}{_{2n}}C_n=\frac{1}{n+1}{_{2n}}C_n=c_n$$
2つ目の証明は最初のものに比べると少しだけ高度ではありますが,
ほぼ計算なしで$(0,0)$から$(n,n)$へのすべての最短経路の
$\frac{1}{n+1}$倍となることが分かります.
命題1を示す.
$(0,0)$から$(n,n)$までのすべての最短経路のうち,$y=x$より
上側でy軸方向に進む回数が$i$回であるものの集合を$T_i$とする.
また,常に領域$x\geq y$を通るものの総数を$a_n$とする.
定義より,
$$|T_0|+|T_1|+\cdots+|T_n|={_{2n}}C_n$$また、$|T_0|=a_n$
$0\le i\le n-1$のとき、$T_i$と$T_{i+1}$が1対1に対応することを示す.
$T_i$の要素について,最初に$y=x$を踏むときの座標を
$(a,a)$とする.この経路を次の3つの部分に分ける.
$p_1$: $(0,0)$から$(a,a-1)$までの経路
$p_2$: $(a,a-1)$から$(a,a)$までの経路
$p_3$: $(a,a)$から$(n,n)$までの経路
ここで、$p_1p_2p_3$の順番を入れ替えて,$p_3p_2p_1$とした経路を考える。
$p_2$の分だけ上にはみ出る部分が増えるので,この経路は$T_{i+1}$の要素になる。
よって、$T_i$と$T_{i+1}$の間で1対1対応が構成できる。
このことから、$|T_0|=|T_1|=\cdots=|T_n|$
$$\therefore a_n=|T_0|=\frac{1}{n+1}{_{2n}}C_n=c_n$$
ここまでは最短経路の総数からうまく対応を見つけて一般項を導いてきましたが,
漸化式から母関数を求めて,計算によって求める事もできます.
母関数とは数列$a_n$に対して,次のように定義される関数のことです.
$$f(x)=\sum_{k=0}^{\infty}a_k x^k$$
数列$a_n$の性質を直接調べることが難しい場合,このような関数を考えて
マクローリン展開などの解析的な手法を使うことで間接的に性質を調べられる場合があります.
漸化式$$
a_0=1,a_{n+1}=\sum_{k=0}^{n}a_k a_{n-k}
$$
で定義される数列$\lbrace a_n \rbrace$が,カタラン数$c_n$に等しいことを示す.
$a_n$の母関数は次のように表される..
$$f(x)=\sum_{k=0}^{\infty}a_k x^k$$
$f(x)^2$の$x^n$の係数を考えると,漸化式よりこれは$$\sum_{i=0}^{n}a_i a_{n-i}=a_{n+1}$$となる.よって,
$$f(x)^2=\sum_{k=0}^{\infty}a_{k+1} x^k$$
すなわち,$f(x)=1+xf(x)^2$
よって,$f(x)=\frac{1\pm\sqrt{1-4x}}{2x}$
$a_0=1$より,$$\lim_{x \to 0}f(x)=1$$である必要があるので,
$f(x)=\frac{1-\sqrt{1-4x}}{2x}$
次に,$g(x)=\sqrt{1-4x}$をマクローリン展開したときの,$x^{n+1}$の係数を求める.
$$g^{(n+1)}(x)=(-4)^{n+1} \frac{1}{2}\left(-\frac{1}{2}\right)\left(-\frac{3}{2}\right)\cdots\left(-\frac{2n-1}{2}\right) (1-4x)^{\frac{2n+1}{2}}$$
$$g^{(n+1)}(0)=(-4)^{n+1}(-1)^n\frac{(2n)!}{2^{n+1} 2^n n!}=-2\frac{(2n)!}{n!}$$
よって,$g(x)$の$x^{n+1}$の係数は$-2\frac{(2n)!}{n!(n+1)!}$だから,
$f(x)$の$x^n$の係数は$\frac{(2n)!}{n!(n+1)!}=\frac{1}{n+1}{_{2n}}C_n=c_n$
よって,$a_n=c_n$が成立
次回からは,タイトル通りカタラン数を様々な形で一般化していこうと思います.