カタラン数とその拡張 その3 〜標準ヤング盤を通したカタラン数の高次元化〜
前回
は,最短経路の問題を通してカタラン数の拡張をしてきました.
今回注目するのは,初回でも紹介したカタラン数の次の性質です.
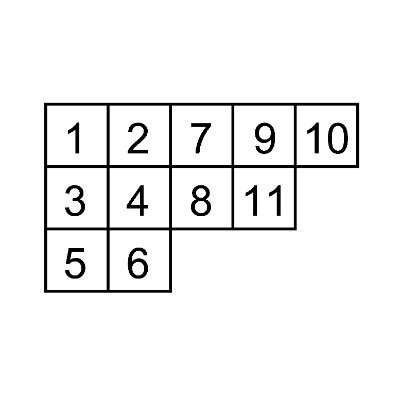
$2\times n$のマス目に$1$から$2n$までの数字を1つずつ書き込むとき,次の条件を満たす方法の総数は,カタラン数$c_n$に等しい
- 横に隣り合う任意の2つのマスについて,左に書かれた数字よりも右に書かれた数字の方が大きい.
- 縦に隣り合う任意の2つのマスについて,上に書かれた数字よりも下に書かれた数字の方が大きい.
今回はこれを拡張して,次のような問題を考えてみましょう.
$m\times n$のマス目に$1$から$mn$までの数字を1つずつ書き込むとき,次の条件を満たす方法の総数を$C_n^m$で表す.
- 横に隣り合う任意の2つのマスについて,左に書かれた数字よりも右に書かれた数字の方が大きい.
- 縦に隣り合う任意の2つのマスについて,上に書かれた数字よりも下に書かれた数字の方が大きい.
$C_n^m$は,最短経路に当てはめれば,次のように意味づけすることもできます.
$\mathbb{R}^m=\{(x_1,x_2,x_3,\cdots,x_m)|\ x_1,x_2,x_3,\cdots,x_m \in\mathbb{R}\}$上の$(0,0,\cdots,0)$から$(n,n,\cdots,n)$への最短経路で,領域$x_1\ge x_2\ge x_3\ge \cdots\ge x_m$内にあるものの総数は,$C_n^m$となる.
$m\times n$のマス目に順番に$1$から$mn$までの数字を順番に書き込んでいくと考え,
最短経路において$x_i$軸方向の移動を$i$行目に数字を書き込むことに対応させれば,
マス目と最短経路の間に1対1対応が構成できる.
よって最短経路の総数は$C_n^m$となる.
今回は,この$C_n^m$を与える式を考えてみます.
フック長の公式
まず準備として,いくつかの用語,記号を定義します.
自然数$N$に対して,自然数の組$(k_1,k_2,k_3,\cdots,k_n)$が
$$
N=k_1+k_2+k_3+\cdots+k_n,\ \ k_1\ge k_2\ge k_3\ge\cdots\ge k_n
$$
を満たすとき,これを自然数$N$の分割(Partition)という.
この分割は,下図のように$i$行目に$k_i$個の正方形を並べた図形として表現できる.
これをヤング図形(Young diagram)という.
![!FORMULA[27][-992523928][0]に対するヤング図形](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2F20220330235618.png?alt=media) $(k_1,k_2,k_3)=(5,4,2)$に対するヤング図形
$(k_1,k_2,k_3)=(5,4,2)$に対するヤング図形
また,ヤング図形に含まれる$1\times 1$の正方形を箱(Box)と呼ぶ.
$i$行$j$列にある箱を$(i,j)$と表す.
1つの分割は1つのヤング図形と1対1に対応する.
自然数$N$の分割に対応するヤング図形の箱に$1$から$N$までの数字を1つずつ書き込むとき,次の条件を満たすものを,標準ヤング盤(Standard young tableaux)あるいは単に標準盤(Standard tableaux)という.
- 横に隣り合う任意の2つのマスについて,左に書かれた数字よりも右に書かれた数字の方が大きい.
- 縦に隣り合う任意の2つのマスについて,上に書かれた数字よりも下に書かれた数字の方が大きい.
ヤング図形$\lambda$に対して,箱の個数を$|\lambda|$,標準ヤング盤の個数を$SYT_\lambda$で表す.また箱$d$がヤング図形$\lambda$に含まれることを$d \in\lambda$で表す.
ヤング図形$\lambda$上の箱$d=(i,j)$に対して,
- 箱$d$
- 同じ列で箱$d$の下にある箱
- 同じ行で箱$d$の右にある箱
をあわせた集合を箱$d$におけるフック(Hook)といい,フックに属する箱の個数をフック長(Hook length)といって,$h_\lambda(d)$あるいは$h_\lambda(i,j)$で表す.
フック長が1である箱を角(Corner)という.
このとき,次の公式が成り立つことが知られています.強すぎです.
ヤング図形$\lambda$について,次が成立する.
$$
SYT_{\lambda} = \frac{|\lambda|!}{\prod_{d \in\lambda}h_\lambda(d)}
$$
ただし,分母の積は,$\lambda$上のすべての箱に対してそのフック長を掛けることを意味する.
証明は難しいですが,理解できないレベルでもないので,この記事の最後に載せようと思います.
まずはこの公式の威力を体感してみましょう.
まず,いろいろ試行錯誤した$c_n$の一般項ですが,フック長の公式を使えば2秒で求められます!
$c_n$は,分割$(k_1,k_2)=(n,n)$に対するヤング図形$\lambda$の標準盤の個数なので,
$$c_n=SYT_{\lambda}
= \frac{|\lambda|!}{\prod_{d \in\lambda}h_\lambda(d)}
= \frac{(2n)!}{(n+1)!n!}=\frac{1}{n+1} {_{2n}}C_n
$$
前回最初に紹介した傾き1の直線の最短経路の総数は,特殊な場合に限定すればこの公式で求められます.
$m\ge n$とする.$(0,0)$から$(m,n)$への最短経路で,直線$y=x$を越えないものの総数は,次のように表せる.
$$\frac{m-n+1}{m+1}{_{m+n}}C_m$$
最短経路において$x$軸方向の移動を,ヤング図形の$1$行目に数字を書き込むことに対応させ,
$y$軸方向の移動を,ヤング図形の$1$行目に数字を書き込むことに対応させると,
求める場合の数は,分割$(k_1,k_2)=(m,n)$に対するヤング図形$\lambda$の標準盤の個数に等しい.
よって,
$$SYT_{\lambda}
= \frac{|\lambda|!}{\prod_{d \in\lambda}h_\lambda(d)}
= \frac{(m+n)!}{\prod_{j_1=1}^{m}h_\lambda(1,j_1)\prod_{j_2=1}^{m}h_\lambda(2,j_2
)}
= \frac{(m+n)!}{\frac{(m+1)!}{m-n+1} n!}
= \frac{m-n+1}{m+1}{_{m+n}}C_m
$$
では早速これを使って,$C_n^m$の一般項をもとめてみましょう!
高次元カタラン数
$C_n^m$は分割$(k_1,k_2,\cdots,k_m)=(n,n,\cdots,n)$に対する標準盤の個数なので,フック長の公式を認めれば簡単に求められます.
$C_n^m$は,次のように表せる.
$$C_n^m=(mn)!\prod_{i=1}^{m}\prod_{j=1}^{n}\frac{1}{i+j-1}=(mn)!\frac{0!}{n!}\frac{1!}{(n+1)!}\frac{2!}{(n+2)!}\cdots\frac{(m-2)!}{(m+n-2)!}\frac{(m-1)!}{(m+n-1)!}$$
超階乗$sf(n)= \prod_{i=1}^{n}i!$を導入すれば,次のようにも表現できる.
$$
C_n^m=\frac{(mn)!\ sf(m-1)\ sf(n-1)}{sf(m+n-1)}
$$
$\lambda$を分割$(k_1,k_2,\cdots,k_m)=(n,n,\cdots,n)$に対するヤング図形とする.フック長の公式より,
$$C_n^m=SYT_{\lambda}
= \frac{|\lambda|!}{\prod_{d \in\lambda}h_\lambda(d)}
= \frac{(mn)!}{\prod_{i=1}^{m}\prod_{j=1}^{n}h_\lambda(i,j)}
= (mn)!\prod_{i=1}^{m}\prod_{j=1}^{n}\frac{1}{i+j-1}
$$
また,これを書き換えると,
$$
C_n^m=(mn)!\prod_{i=1}^{m}\prod_{j=1}^{n}\frac{1}{i+j-1}
=(mn)!\prod_{i=1}^{m}\frac{(i-1)!}{(i+n-1)!}=\frac{(mn)!\ sf(m-1)\ sf(n-1)}{sf(m+n-1)}
$$
フック長の公式の証明
フック長の公式にはいくつかの証明が知られていますが,ここでは1979年に発見されたC.Greene, A.Nijenhuis, H.S.Wilfらによる証明を紹介します.
フック長の積について成り立つべき漸化式を考え,それに確率論的な解釈を与えるというものです.
証明
まず,次の補題が成り立つ.
$$
SYT_\lambda = \sum_{c\in \lambda, h_\lambda(c)=1}SYT_{\lambda\setminus\{c\}}
$$
ただし右辺の総和は,ヤング図形$\lambda$に対して,どこかの角を取り除いたヤング図形全体に対して,その標準盤の個数を足し合わせることを意味する.
$N$個の箱を持つヤング図形$\lambda$では,その標準盤において$N$はどこかの角に存在する.
$N$が角$c$にある$\lambda$の標準盤の個数は,$\lambda$から角$c$を取り除いて得られるヤング盤$\lambda\setminus\{c\}$の標準盤の個数に等しい.よって補題は成立する.
ヤング図形$\lambda$に対し,$H_\lambda=\prod_{c\in \lambda}h_\lambda(c)$とする.
また,$l$個の角$c_k=(\alpha_k,\beta_k)\ (k=1,2,3,\cdots,l)$を持つヤング図形$\lambda$に対し,$\lambda$から$c_k$を取り除いたヤング図形を$\lambda_k$とする.
$|\lambda|=1$の場合は$SYT_\lambda=\frac{1!}{H_\lambda}=1$が成り立つことと,
補題6に注意すれば,次のことが成り立てば良いとわかる.
主張
$n$個の箱をもつヤング図形$\lambda$において,
$$
\frac{n!}{H_\lambda} = \sum_{k=1}^{l} \frac{(n-1)!}{H_{\lambda_k}}
$$
が成立する.
ここで,この式を変形すると,
$$
\frac{n!}{H_\lambda} = \sum_{k=1}^{l} \frac{(n-1)!}{H_{\lambda_k}}
\Longleftrightarrow
\frac{1}{n} \sum_{k=1}^{l} \frac{H_\lambda}{H_{\lambda_k}} = 1
$$
となり,右辺は全確率空間と考えることができる.
これに確率論的解釈を与えてみよう.
まず,次のような試行を考える
$\lambda$を$n$個の箱をもつヤング図形とする.次のような操作を考える.
この操作をフックウォーク(Hook walk)という.
- $\lambda$から箱を無作為に$1$つ選ぶ.
- 前に選んだ箱のフックの中にあり,それとは異なる箱を無作為に$1$つ選ぶ.
- (ii)を繰り返す.
このとき,必ず有限回の操作でどこかの角に到達する.
角$c=(\alpha,\beta)$に到達する確率を$p_\lambda(c)$あるいは$p_\lambda(\alpha,\beta)$で表す.
実はこのとき,
$$p_\lambda(c_k)=\frac{1}{n} \frac{H_\lambda}{H_{\lambda_k}}$$
が成り立つ.
これを証明できれば,左辺の総和は全確率空間であって$1$に等しいので,フック長の公式が証明できたことになる.
まずは右辺について詳しく見ていく.
$h_{\lambda_k}$は$h_\lambda$から角$(\alpha_k,\beta_k)$を取り除いたものなので,$h_{\lambda_k}$と$h_\lambda$のフック長の間には次の関係がある.
$$
h_{\lambda_k}(i,j)=
\begin{eqnarray}
\left\{
\begin{array}{l}
h_\lambda(i,j)-1\ \ \ \ \ \ i=\alpha_k \lor j=\beta_k \\
h_\lambda(i,j)\ \ \ \ \ \ \ \ \ \ \ \ \ otherwise.
\end{array}
\right.
\end{eqnarray}
$$
したがって,$i=\alpha_k \lor j=\beta_k$以外においては分母と分子がキャンセルすることと,$h_\lambda(\alpha_k,\beta_k)=1$に注意して,
$$
\frac{H_\lambda}{H_{\lambda_k}}
=\prod_{i=1}^{\alpha_k-1}\frac{h_\lambda(i,\beta_k)}{h_\lambda(i,\beta_k)-1} \prod_{j=1}^{\beta_k-1}\frac{h_\lambda(\alpha_k,j)}{h_\lambda(\alpha_k,j)-1}
=\prod_{i=1}^{\alpha_k-1}\left(1+\frac{1}{h_\lambda(i,\beta_k)-1}\right)\prod_{j=1}^{\beta_k-1}\left(1+\frac{1}{h_\lambda(\alpha_k,j)-1}\right)
$$
を得る.
次に,左辺について考えてみる.
始点を$(i_1, j_1)$に固定したフックウォークについて考える.
$k$回目に選んだ箱を$(i_k,j_k)\ (i=1,2,\cdots,m)$で表すとする.
これに対し,集合$A,B$を次のように定める.(ただし重複は無視する)
$$
A=\{i_1,i_2,\cdots,i_m\}\\
B=\{j_1,j_2,\cdots,j_m\}
$$
つまり,$A$はフックウォークの経路に現れる行番号からなる集合で,$B$は列番号からなる集合である.
このとき,始点が$(i_1,j_1)$であるという条件の下で行番号の集合が$A$,列番号の集合が$B$となる条件付き確率を$p(A,B)$で表す.
これに対し,次の補題が成り立つ.
$$A=\{a_1,a_2,\cdots,a_p\},B=\{b_1,b_2,\cdots,b_q\}$$
とする.ただし,$a_1< a_2<\cdots< a_p, b_1< b_2<\cdots< b_q$
このとき,次が成立する.
$$
p(A,B)=\prod_{s=1}^{p-1}\frac{1}{h_\lambda(a_s,b_q)-1} \prod_{s=1}^{q-1}\frac{1}{h_\lambda(a_p,b_s)-1}
$$
行番号の集合が$A$,列番号の集合が$B$であり,最初に選ぶ箱が$(a_1,b_1)$であることから,
2つ目に選ぶ箱は$(a_1,b_2)$あるいは$(a_2,b_1)$であり,これらが選ばられる確率は$\frac{1}{h_\lambda(a_1,b_1)-1}$である.
また,2つ目の箱として$(a_1,b_2)$を選んだ時,$(a_1,b_2)$からスタートしたものとみなせば,行番号の集合は$A$,列番号の集合が$B\setminus \{b_1\}$ということになる.$(a_1,b_2)$を選んだ場合も同様.
よって,$p(A,B)$には次の漸化式が成り立つ事がわかる.
$$p(A,B)=\frac{1}{h_\lambda(a_1,b_1)-1}
\left\{p(A\setminus\{a_1\},B)+p(A,B\setminus\{b_1\})\right\}$$
これを使って,補題が成り立つことを$|A|+|B|$に関する数学的帰納法で証明する.
- $|A|+|B|=2$のとき
$A={a_1},B={b_1}$であり,左辺の確率は$1$,右辺は空積で$1$なので成立. - $|A|+|B|=n-1$のとき成立すると仮定して,$|A|+|B|=n$のとき
漸化式より,
$$ p(A,B)=\frac{1}{h_\lambda(a_1,b_1)-1} \left(p(A\setminus\{a_1\},B)+p(A,B\setminus\{b_1\})\right)\\ =\frac{1}{h_\lambda(a_1,b_1)-1}\left\{\prod_{s=2}^{p-1}\frac{1}{h_\lambda(a_s,b_q)-1}\prod_{s=1}^{q-1}\frac{1}{h_\lambda(a_p,b_s)-1}+\prod_{s=1}^{p-1}\frac{1}{h_\lambda(a_s,b_q)-1}\prod_{s=2}^{q-1}\frac{1}{h_\lambda(a_p,b_s)-1}\right\}\\ =\frac{h_\lambda(a_p,b_1)-1+h_\lambda(a_1,b_q)-1}{h_\lambda(a_1,b_1)-1}\prod_{s=1}^{p-1}\frac{1}{h_\lambda(a_s,b_q)-1}\prod_{s=1}^{q-1}\frac{1}{h_\lambda(a_p,b_s)-1} $$
ここで,$a_1$行目の長さを$u$,$b_1$列目の長さを$v$とする.
$a_p$行目の長さは$b_q$,$b_q$列目の長さは$a_p$であることも合わせて,
$h_\lambda(a_1,b_1)-1=u+v-a_1-b_1$
$h_\lambda(a_p,b_1)-1=b_q+v-a_p-b_1$
$h_\lambda(a_1,b_q)-1=u+a_p-a_1-b_q$
であるから,$h_\lambda(a_1,b_1)-1=h_\lambda(a_p,b_1)-1+h_\lambda(a_1,b_q)-1$が成り立つ.よって,
$$ p(A,B)=\prod_{s=1}^{p-1}\frac{1}{h_\lambda(a_s,b_q)-1}\prod_{s=1}^{q-1}\frac{1}{h_\lambda(a_p,b_s)-1} $$
よって,補題は示された.
それではこれらを使って証明を完成させよう
$$
\frac{H_\lambda}{H_{\lambda_k}}
=\prod_{i=1}^{\alpha_k-1}\left(1+\frac{1}{h_\lambda(i,\beta_k)-1}\right)\prod_{j=1}^{\beta_k-1}\left(1+\frac{1}{h_\lambda(\alpha_k,j)-1}\right)
$$
であることは証明したので,この式の右辺を展開する.まず,
$$
\prod_{i=1}^{\alpha_k-1}\left(1+\frac{1}{h_\lambda(i,\beta_k)-1}\right)=\sum_{A'\subset\{1,2,\cdots,\alpha_k-1\}}\prod_{a\in A'}\frac{1}{h_\lambda(a,\beta_k)-1}
$$
が成り立つ.ここで,右辺の和において$A'$は$\{1,2,\cdots,\alpha_k-1\}$の部分集合全体を動く.$A'$に$\alpha_k$を加えた集合を$A$とすると,
$$
\prod_{i=1}^{\alpha_k-1}\left(1+\frac{1}{h_\lambda(i,\beta_k)-1}\right)=\sum_{A}\prod_{a\in A, a\neq \alpha_k}\frac{1}{h_\lambda(a,\beta_k)-1}
$$
となる.ただし$A$は${1,2,3,\cdots,\alpha_k}$の部分集合であって$\alpha_k$を含むもの全体を動く.同様に,
$$
\prod_{j=1}^{\beta_k-1}\left(1+\frac{1}{h_\lambda(\alpha_k,j)-1}\right)=\sum_{B}\prod_{b\in B, b\neq \beta_k}\frac{1}{h_\lambda(\alpha_k,b)-1}
$$
であるから,
$$
\frac{H_\lambda}{H_{\lambda_k}}
=\sum_{(A,B)} \prod_{a\in A, a\neq \alpha_k}\frac{1}{h_\lambda(a,\beta_k)-1} \prod_{b\in B, b\neq \beta_k}\frac{1}{h_\lambda(\alpha_k,b)-1}
$$
となる.補題7を使うと,
$$
\frac{1}{n} \frac{H_\lambda}{H_{\lambda_k}}=\frac{1}{n} \sum_{(A,B)}p(A,B)
$$
を得る.ここで最初に箱$(a_1,b_1)$を選ぶ確率は$\frac{1}{n}$で,$(A,B)$をすべて動かせば$(\alpha_k,\beta_k)$に達する経路の確率をすべて足すことになるので,この式の右辺は$p_\lambda(c_k)$に等しい.よってフック長の公式は示された.$\blacksquare$
いかかでしたでしょうか.最後はなかなか大変な証明になりましたが,これを機にカタラン数の面白さがわかってもらえたら嬉しいです.