位相空間の連結性と連結集合

位相空間論

5673

本稿では，位相空間が連結であること，および連結集合の定義を述べる．その後，連結集合を特徴づける1つの命題を証明する．

位相空間の連結性

位相空間が連結であることの定義はいくつかあるが，ここでは次の定義を採用する．

位相空間の連結性

位相空間 $(X, O)$ が連結（connected）であるとは， $X$ の部分集合であって， $(X, O)$ の開集合かつ閉集合であるものが，空集合 $\emptyset$ と $X$ のみであることをいう．

記号の意味

位相空間 $(X, O)$ という場合， $O$ は $X$ の位相を表すものとする．

位相の定義を知っていれば，上記の定義は極めてシンプルである．しかし，連結性の直感的な意味，すなわち「つながっている」という感覚を，この定義から受け取るのは難しいだろう．後述する連結集合の特徴づけは，この困難さを解消するものである．文献によっては，その特徴づけを連結性の定義とすることもある．

連結集合

連結集合を定義するには，部分空間の概念が必要である．念のため，部分空間の定義を述べておく．

相対位相と部分空間

$(X, O)$ を位相空間とする． $X$ の空でない部分集合 $A$ に対して
$O_{A} = {U \cap A ∣ U \in O}$
と定めると， $O_{A}$ は $A$ の1つの位相である．この位相 $O_{A}$ を集合 $A$ 上の $O$ に関する相対位相（relative topology）という．また，位相空間 $(A, O_{A})$ を，位相空間 $(X, O)$ の部分空間（subspace）という．

部分空間という用語について

部分空間という言葉は複数の文脈で用いられうる．それは「線形部分空間（linear subspace）」かもしれないし，本稿での意味「部分位相空間（topological subspace）」かもしれない．このように，同じ言葉でも異なる意味で使われる場合があるので，数学に関する文献を読むときには気を付けるとよい．

相対位相

定義2の $O_{A} = {U \cap A ∣ U \in O}$ が $A$ の位相であることを示せ．

連結集合

$(X, O)$ を位相空間とする． $X$ の空でない部分集合 $A$ が $(X, O)$ の連結集合（connected set）であるとは， $A$ が（相対位相に関する）部分空間として連結であることをいう．すなわち，集合 $A$ 上の $O$ に関する相対位相を $O_{A}$ とするとき，位相空間 $(A, O_{A})$ が連結であることをいう．

上記の定義は，先述した位相空間の連結性の定義に基づくものであるため，同様のわかりづらさを抱えている．これを解消するのが，次に示す特徴づけである．

連結集合の特徴づけ

ここでは，連結集合を特徴づける1つの命題を証明する．

連結集合の特徴づけ

$(X, O)$ を位相空間， $A$ を $X$ の空でない部分集合とするとき，次の2つの条件は同値である．

$A$ は $(X, O)$ の連結集合である．
任意の $U, V \in O$ に対して， $U, V$ が次の3つを満たすならば， $U \cap V \cap A \neq \emptyset$ である．
- $U \cap A \neq \emptyset$
- $V \cap A \neq \emptyset$
- $A \subset U \cup V$

命題1の条件2について

命題1の条件2を論理記号で書くと次の通りである．こう書いた方が主張としてはわかりやすいかもしれない．
$\forall (U, V \in O), [(U \cap A \neq \emptyset) \land (V \cap A \neq \emptyset) \land (A \subset U \cup V) \Rightarrow U \cap V \cap A \neq \emptyset]$

証明へ入る前に，命題1の条件2について直感的な図解をしておこう．
$A$ が「つながって」いる，すなわち連結集合であれば，条件2の3項目を満たす $U, V$ を取ると，図1のように必ず $U \cap V \cap A \neq \emptyset$ となる．

Aが連結集合であるとき

一方， $A$ が「つながって」いない，すなわち連結集合でなければ，条件2の3項目を満たす $U, V$ を取っても，図2のように $U \cap V \cap A = \emptyset$ となることがある．

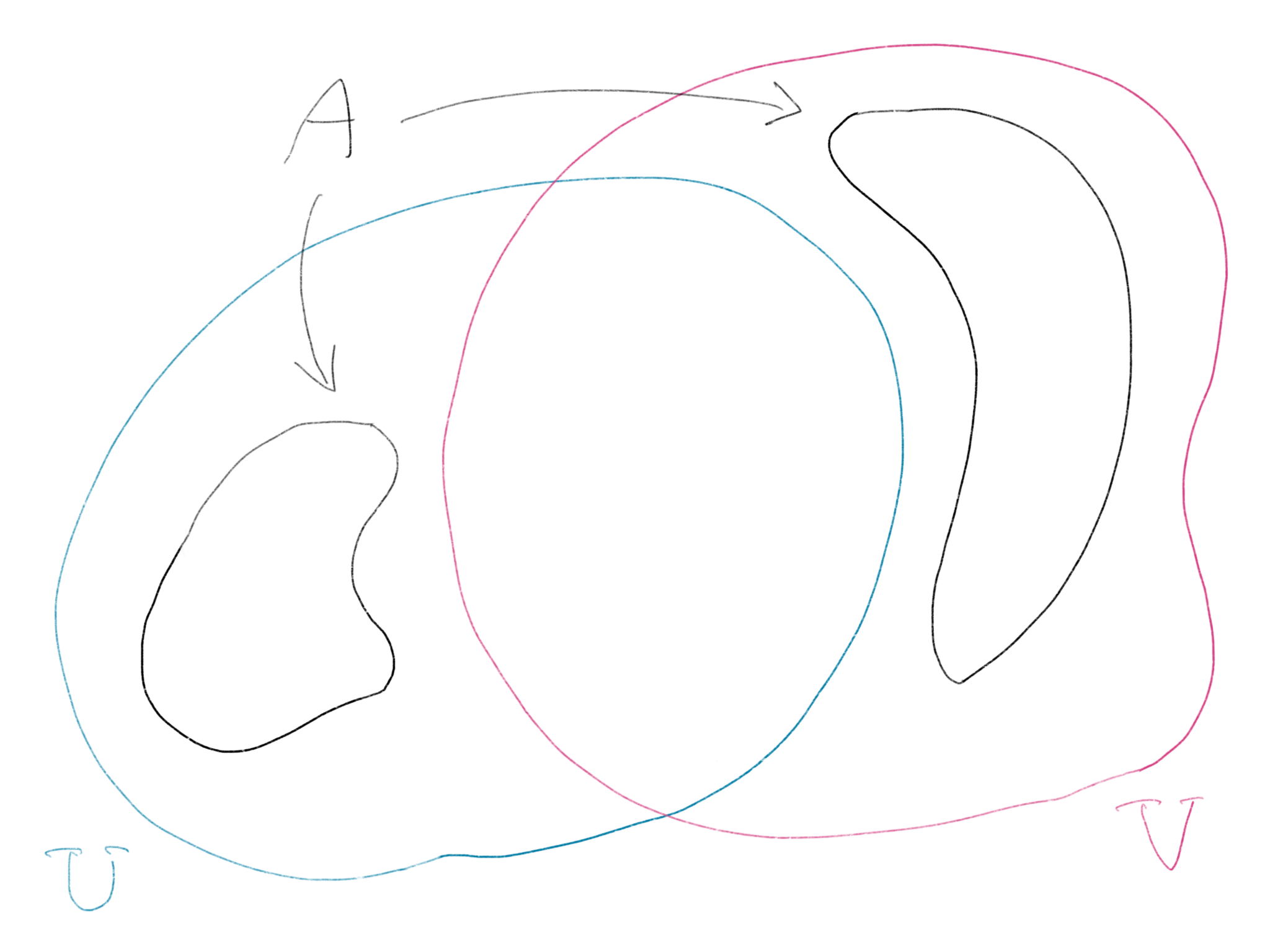Aが連結集合でないとき

以下，命題1を証明するが，議論自体は抽象的である．数学においては，証明を追うだけでなく，もとの主張が意味するところを理解しておくことも重要である．上のような簡単な図を自分で描いてみるだけでも，定理や命題の意味を掴むきっかけになるはずだ．

命題1

以下，集合 $A$ 上の $O$ に関する相対位相を $O_{A}$ とする．

（1 $\Rightarrow$ 2）
$A$ を $(X, O)$ の連結集合とする．さらに， $U, V \in O$ は次の3つを満たすとする．

$U \cap A \neq \emptyset$
$V \cap A \neq \emptyset$
$A \subset U \cup V$

このとき， $U, V$ はともに空でない．また， $U, V$ の少なくとも一方が $X$ のときは， $U \cap V \cap A \neq \emptyset$ が直ちに成り立つ．そこで，以下では $U, V \notin {\emptyset, X}$ とする． $A \subset U \cup V$ より
$(U \cap A) \cup (V \cap A) = (U \cup V) \cap A = A$
である．一方， $A$ は $(X, O)$ の連結集合かつ $U, V \notin {\emptyset, X}$ であるから， $U \cap A$ と $V \cap A$ はともに $(A, O_{A})$ の閉集合ではない．

以上を踏まえて，背理法により $U \cap V \cap A \neq \emptyset$ であることを示そう．
もし， $U \cap V \cap A = \emptyset$ であるとすると，
$(U \cap A) \cap (V \cap A) = U \cap V \cap A = \emptyset$
である．これと $(U \cap A) \cup (V \cap A) = A$ より $U \cap A = A ∖ (V \cap A)$ であるが，これは $V \cap A$ が $(A, O_{A})$ の閉集合ではないことに矛盾する．従って $U \cap V \cap A \neq \emptyset$ である．

（2 $\Rightarrow$ 1）
任意の $U, V \in O$ に対して
$(U \cap A \neq \emptyset) \land (V \cap A \neq \emptyset) \land (A \subset U \cup V) \Rightarrow U \cap V \cap A \neq \emptyset$
が成り立つとする． $U_{A} \notin {\emptyset, A}$ を $(A, O_{A})$ の開集合とすると， $U_{A} = U \cap A$ を満たす $U \in O ∖ {\emptyset, X}$ が存在する．

以上を踏まえて，背理法により $U_{A}$ が $(A, O_{A})$ の閉集合ではないことを示そう．
もし， $U_{A}$ が $(A, O_{A})$ の閉集合であるとすると， $V_{A} = A ∖ U_{A} \notin {\emptyset, A}$ も $(A, O_{A})$ の開集合である．よって， $V_{A} = V \cap A$ を満たす $V \in O ∖ {\emptyset, X}$ が存在する．このとき，次の2つが言える．

$U \cap A = U_{A} \neq \emptyset$
$V \cap A = V_{A} \neq \emptyset$

さらに
$A = U_{A} \cup V_{A} = (U \cap A) \cup (V \cap A) = (U \cup V) \cap A$
より $A \subset U \cup V$ である．ゆえに，最初の仮定から
$U_{A} \cap V_{A} = (U \cap A) \cap (V \cap A) = U \cap V \cap A \neq \emptyset$
が成り立つが，これは $V_{A} = A ∖ U_{A}$ であることに矛盾する．従って $U_{A}$ は $(A, O_{A})$ の閉集合ではない．
以上より， $A$ は $(X, O)$ の連結集合である．

命題1の応用として，位相空間の連結性に連結集合と同様の特徴づけを与えることができる．これは，読者への演習問題とする．

位相空間の連結性の特徴づけ

$(X, O)$ を位相空間とするとき，次の2つの条件は同値であることを示せ．

$(X, O)$ は連結である．
任意の $U, V \in O$ に対して， $U, V$ が次の3つを満たすならば， $U \cap V \neq \emptyset$ である．
- $U \neq \emptyset$
- $V \neq \emptyset$
- $X = U \cup V$

問題の解答

問題1

$\emptyset = \emptyset \cap A \in O_{A}$ ， $A = X \cap A \in O_{A}$ である．
$O_{1}, O_{2}, \dots, O_{n} \in O_{A}$ とすると，各 $i = 1, 2, \dots, n$ に対して $O_{i} = U_{i} \cap A$ を満たす $U_{i} \in O$ が存在する．このとき， $⋂_{i = 1}^{n} U_{i} \in O$ が成り立つから
$⋂_{i = 1}^{n} O_{i} = ⋂_{i = 1}^{n} (U_{i} \cap A) = (⋂_{i = 1}^{n} U_{i}) \cap A \in O_{A}$
である．
${O_{λ}}_{λ \in Λ}$ を $O_{A}$ の元からなる集合族とすると，各 $λ \in Λ$ に対して $O_{λ} = U_{λ} \cap A$ を満たす $U_{λ} \in O$ が存在する．このとき， $⋃_{λ \in Λ} U_{λ} \in O$ が成り立つから
$⋃_{λ \in Λ} O_{λ} = ⋃_{λ \in Λ} (U_{λ} \cap A) = (⋃_{λ \in Λ} U_{λ}) \cap A \in O_{A}$
である．

以上より， $O_{A}$ は $A$ の位相の定義をすべて満たす，すなわち $A$ の位相である．

問題2

命題1は， $X$ の空でない部分集合 $A$ に対して成り立つから，特に $A = X$ でも成り立つ．すなわち，次の2つの条件は同値である．

$X$ は $(X, O)$ の連結集合である．
任意の $U, V \in O$ に対して， $U, V$ が次の3つを満たすならば， $U \cap V \cap X \neq \emptyset$ である．
- $U \cap X \neq \emptyset$
- $V \cap X \neq \emptyset$
- $X \subset U \cup V$

1つ目の「 $X$ は $(X, O)$ の連結集合である」とは，連結集合の定義より $(X, O)$ が連結であることに他ならない．また，2つ目に現れる各式は， $U, V$ がともに $X$ の部分集合であることに注意すると，次のように置き換えられる．
$\begin{aligned} U \cap V \cap X \neq \emptyset & \to U \cap V \neq \emptyset \\ U \cap X \neq \emptyset & \to U \neq \emptyset \\ V \cap X \neq \emptyset & \to V \neq \emptyset \\ X \subset U \cup V & \to X = U \cup V \end{aligned}$
従って，次の2つの条件は同値である．