離散位相の「離散」ってなんだよ！！！！！！！！！！！！！！！
どうも
こんにちは B4になった事実に耐えられないごててんです.
位相空間の勉強を始めると, すぐに離散位相と密着位相に出会うと思います. さて, 説明なしにこの言葉に出会うとこの気持ちが湧いてくるでしょう
「離散要素、どこ？？？？？？？？？？？？？？？？？？？？？」
「密着要素、どこ？？？？？？？？？？？？？？？？？？？？？」
「どっちが離散でどっちが密着だっけ？？？？？？？？？？？？」
記事の目的
この記事では, 離散位相と密着位相を見たときに幾何的なイメージが湧いて出るような解釈を与えることを目的として位相空間論を進めていきます！
この記事を読めば, 離散位相を見て「離散だわ～」密着位相を見て「密着だわ～」としか思わなくなります！！！！！！！！！！（自信過多）
この記事は「厳密さ関係なしのイメージ」や「強引な解釈」を多分に含みます！
苦手な方はブラウザバック推奨です！
ユークリッド空間の開集合
イメージを説明するために, 一旦$2$次元ユークリッド空間の開集合を考えます. 開集合はイメージ的には「境界」のない集合のことでした.
開集合のわかりやすい例として, 原点からの距離が$1$未満の点の全体があると思います.
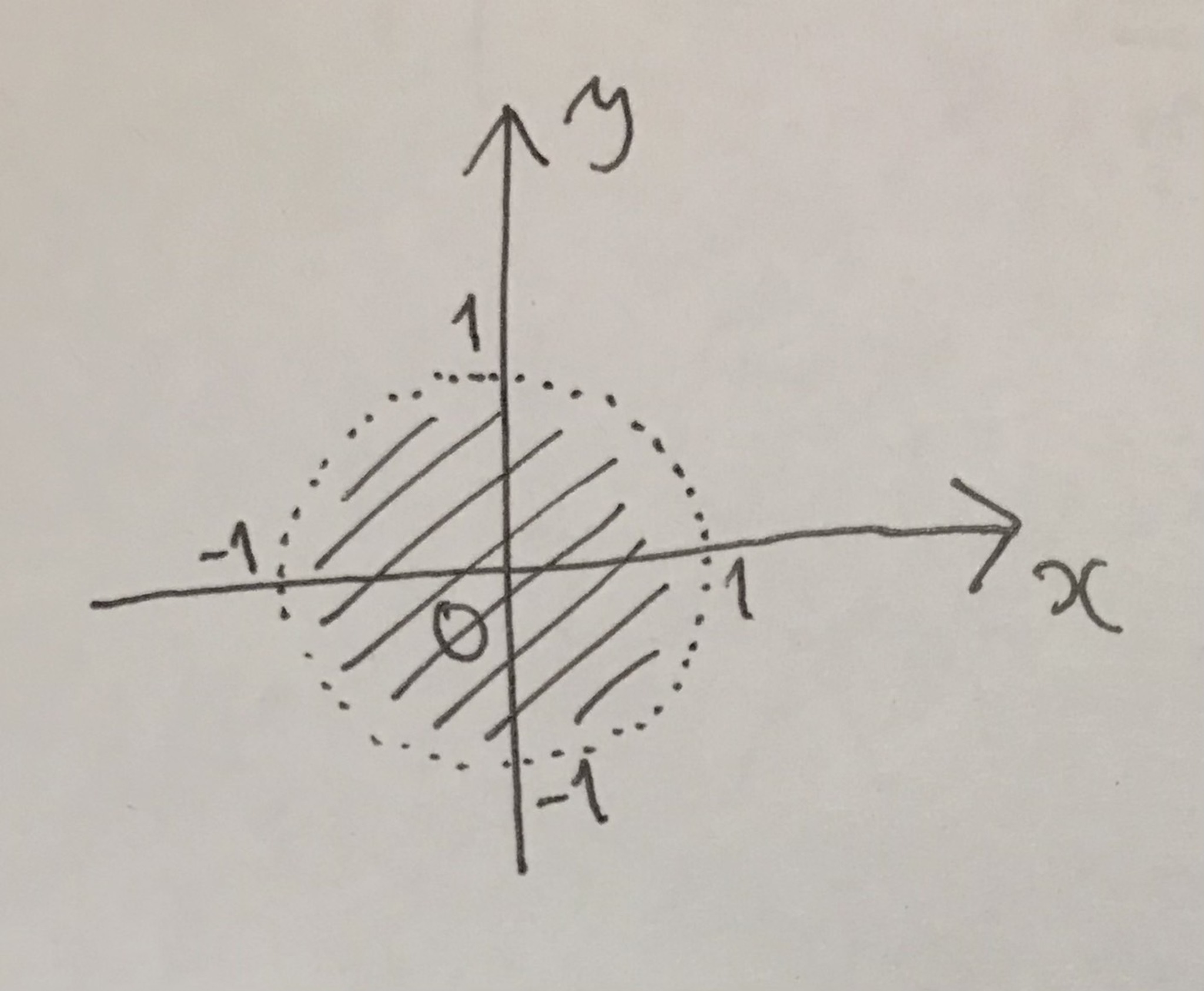手書き
他にもこういった開集合があります.
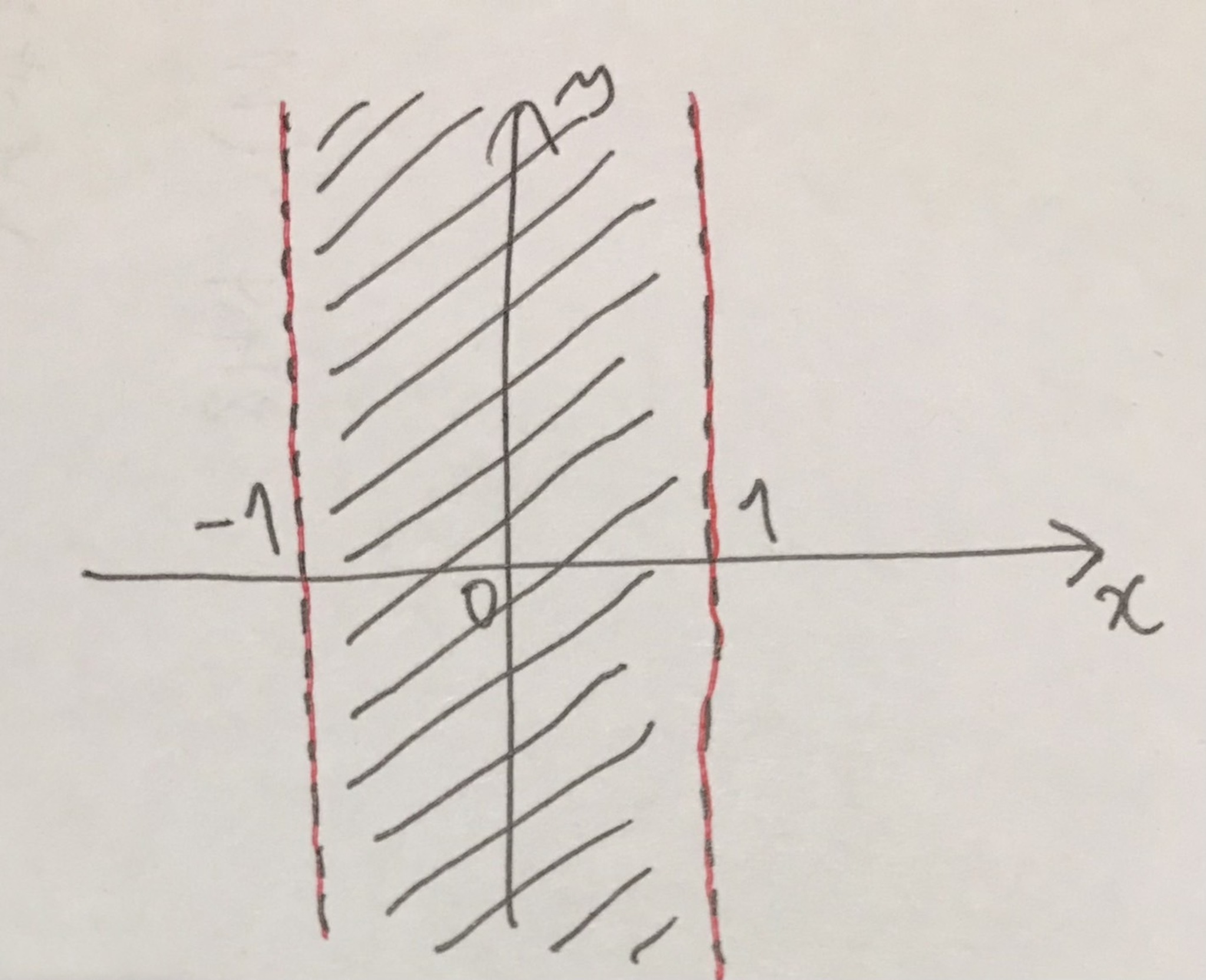
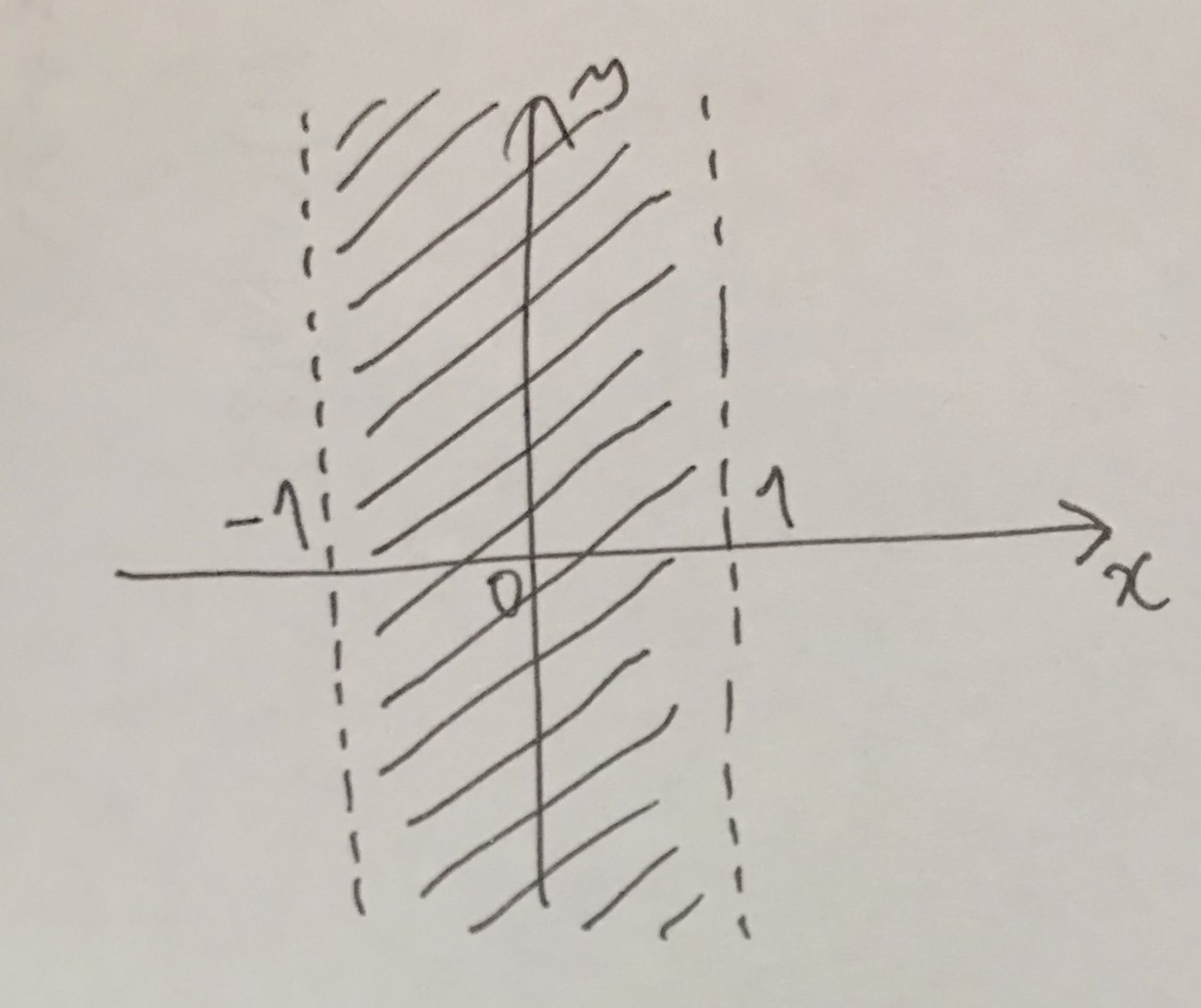x座標の絶対値が1未満の点全体
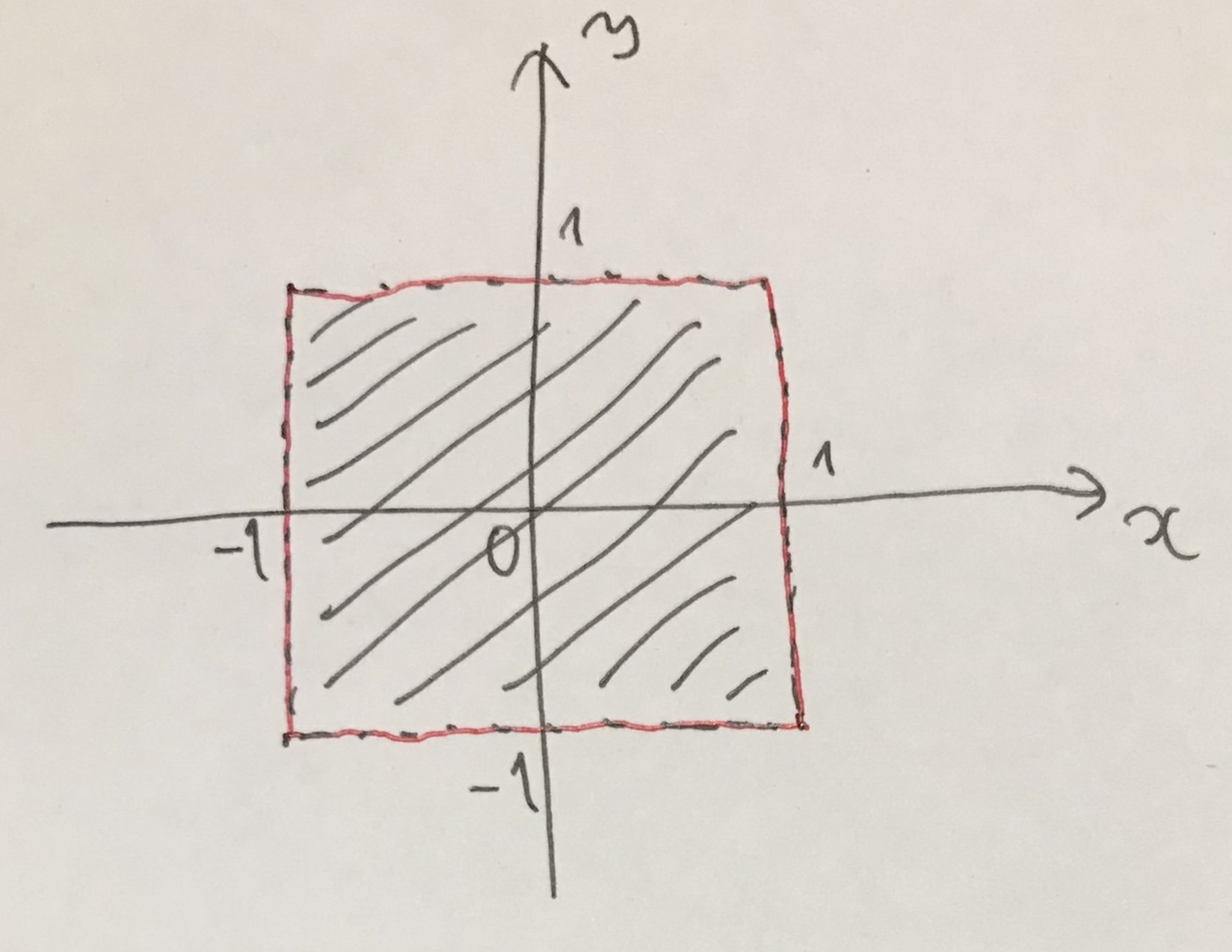
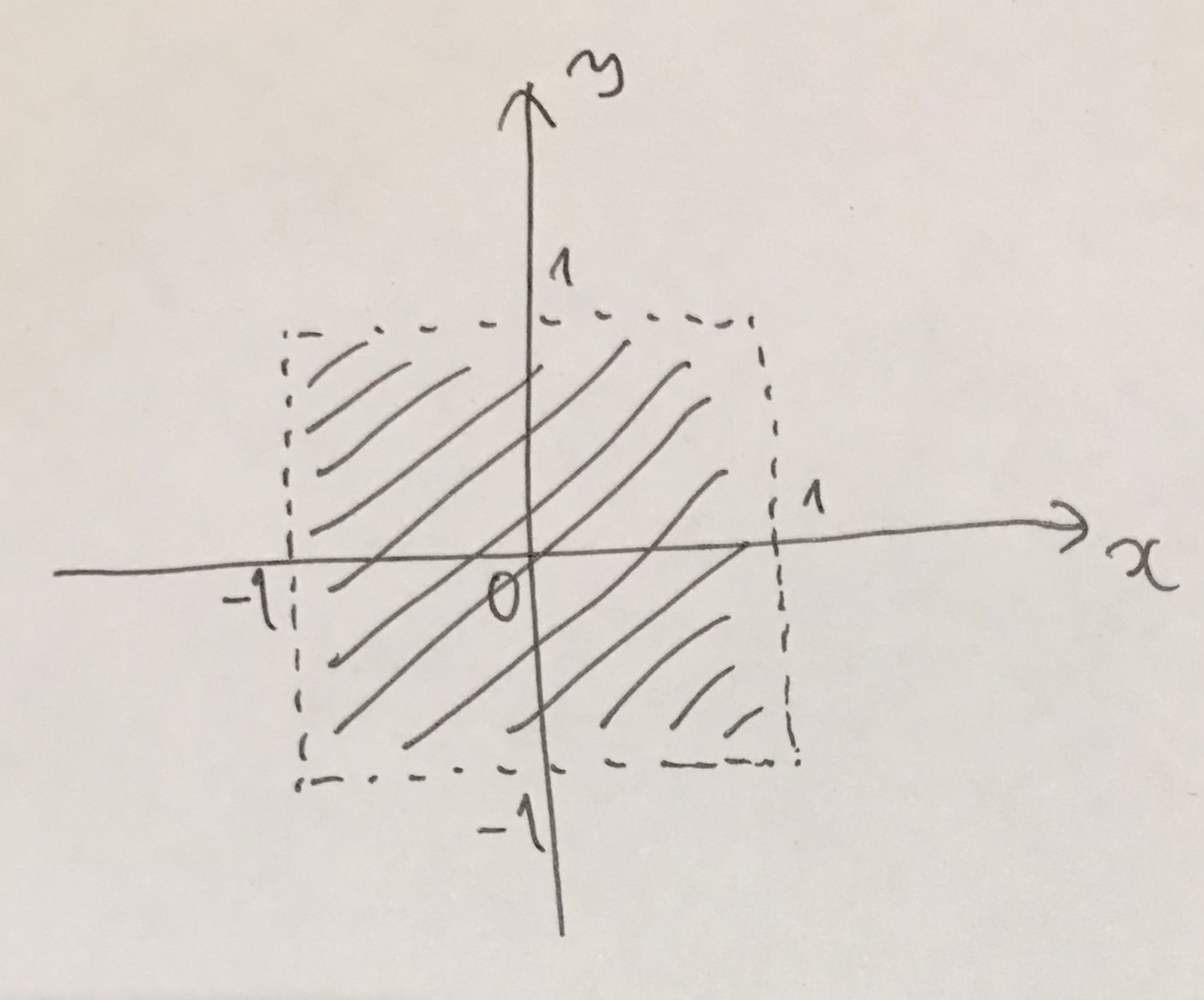x座標の絶対値とy座標の絶対値がともに1未満の点全体
この記事ではこれらの開集合の「境界」に着目します.
開集合は, 境界がない図形というイメージがあります. これを「輪っかで囲める範囲」と解釈します.
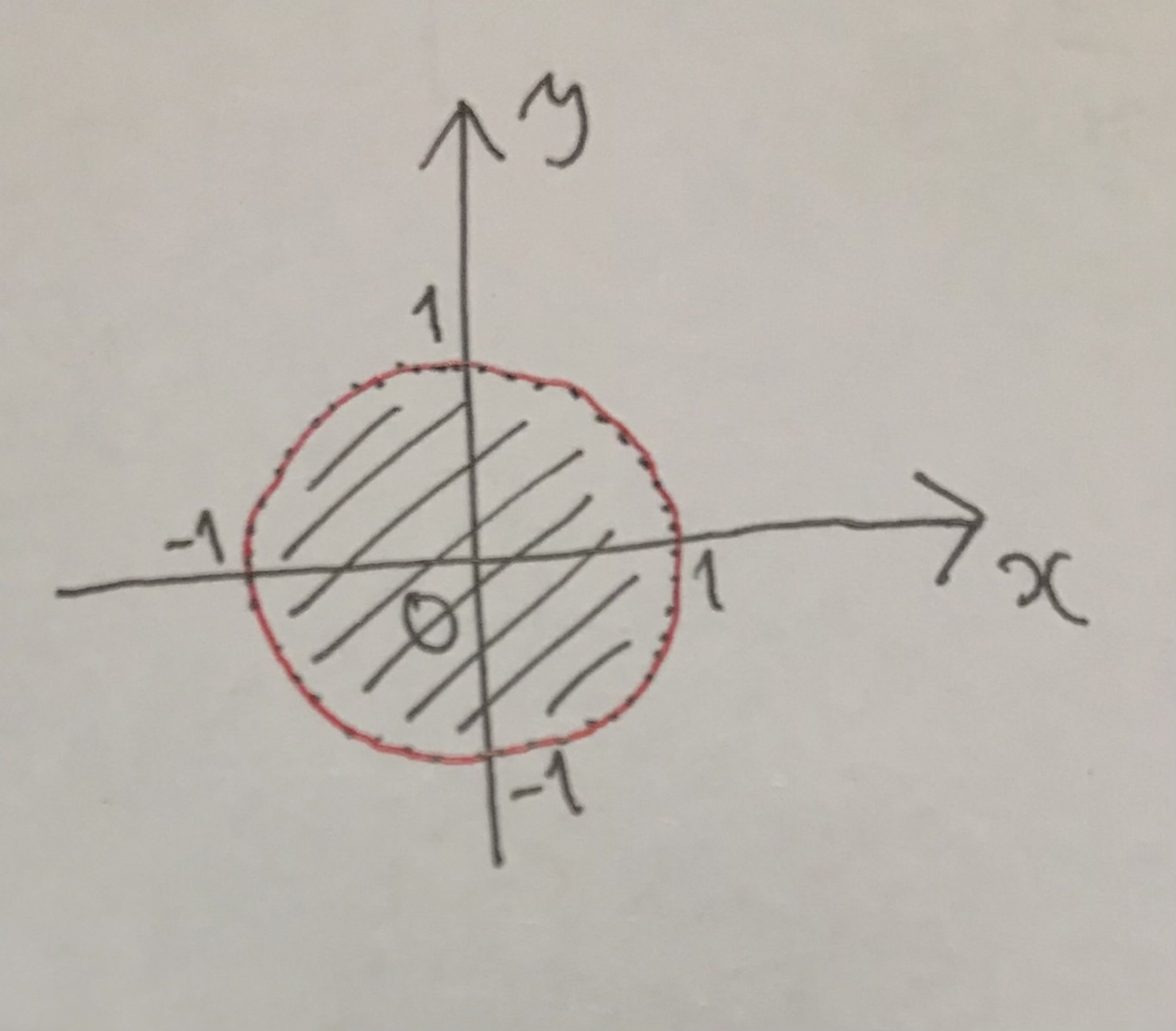輪っかっぽい
好意的に解釈すれば無限大まで伸ばした輪っか
滑らかではないが
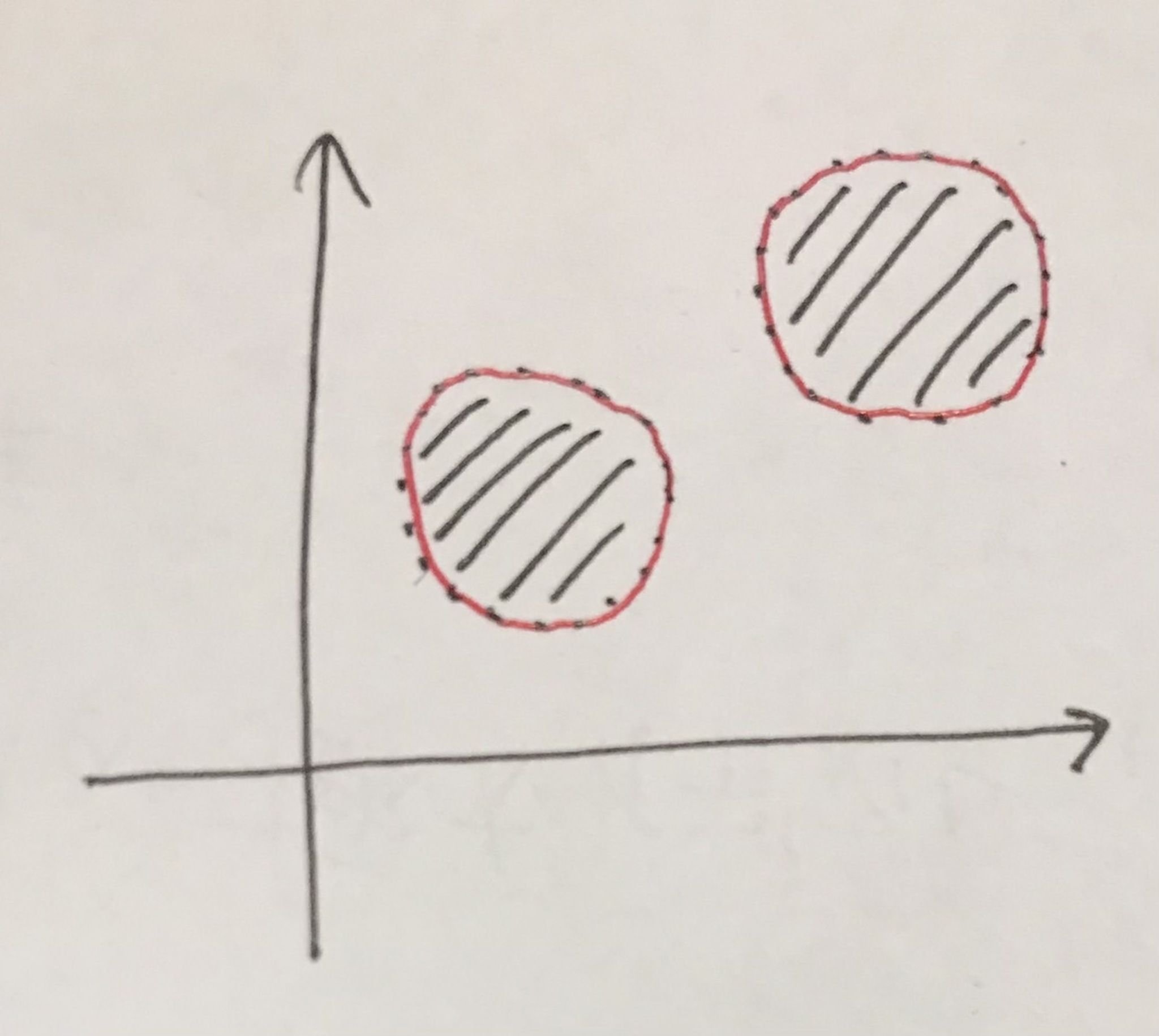複数の輪っかを使ってもいいことにします
位相空間ってなんだっけ？
位相は開集合系, つまり「開集合をすべて集めてきたもの」です
つまり位相は「輪っかで囲んだ図形をすべて集めてきたもの」と（強引ですが）解釈できます！
$X$を空でない集合, $\mathcal{O}$を$X$の部分集合を元とする集合（$X$の冪集合$2^X,P(X)$の部分集合のこと）について, 次の$(1)$-$(3)$が成立するとき, $X$,また組$(X,\mathcal{O})$を位相空間とよび, $\mathcal{O}$の元を開集合, $X$の元を点とよぶ.
$(1)$ $X,\emptyset \in \mathcal{O}.$
$(2)$ $O_1 , O_2 \in \mathcal{O}$ とするとき, $O_1 \cap O_2 \in \mathcal{O}.$
$(3)$ $\{ O_{\lambda} \}_{\lambda \in \Lambda}$ を$\Lambda$を添え字とする$\mathcal{O}$の元の族とするとき,
$$
\hspace{15pt} \bigcup_{\lambda \in \Lambda} O_{\lambda} \in \mathcal{O}.
$$
離散位相を解釈する
離散位相を定義します.
$X$を空でない集合とするとき, そのベキ集合$2^X$を開集合とする位相空間$(X,2^X)$を離散位相という.
離散っぽい要素を考えてみます. 開集合が$2^X$であるということは, すべての部分集合が開集合となるということです.
以下イメージしやすいよう, 特に$\mathbb{R}$の離散位相$(\mathbb{R},2^{\mathbb{R}})$で考えます.
離散位相における開集合$\{0\}$を考えてみましょう. すべての部分集合が開集合なので, $\{0\}$も当然開集合です.
$\{0\}$が開集合であるということは, 「$0$のみを囲む輪っか」が描けるということです
これは次の図のように解釈できます.
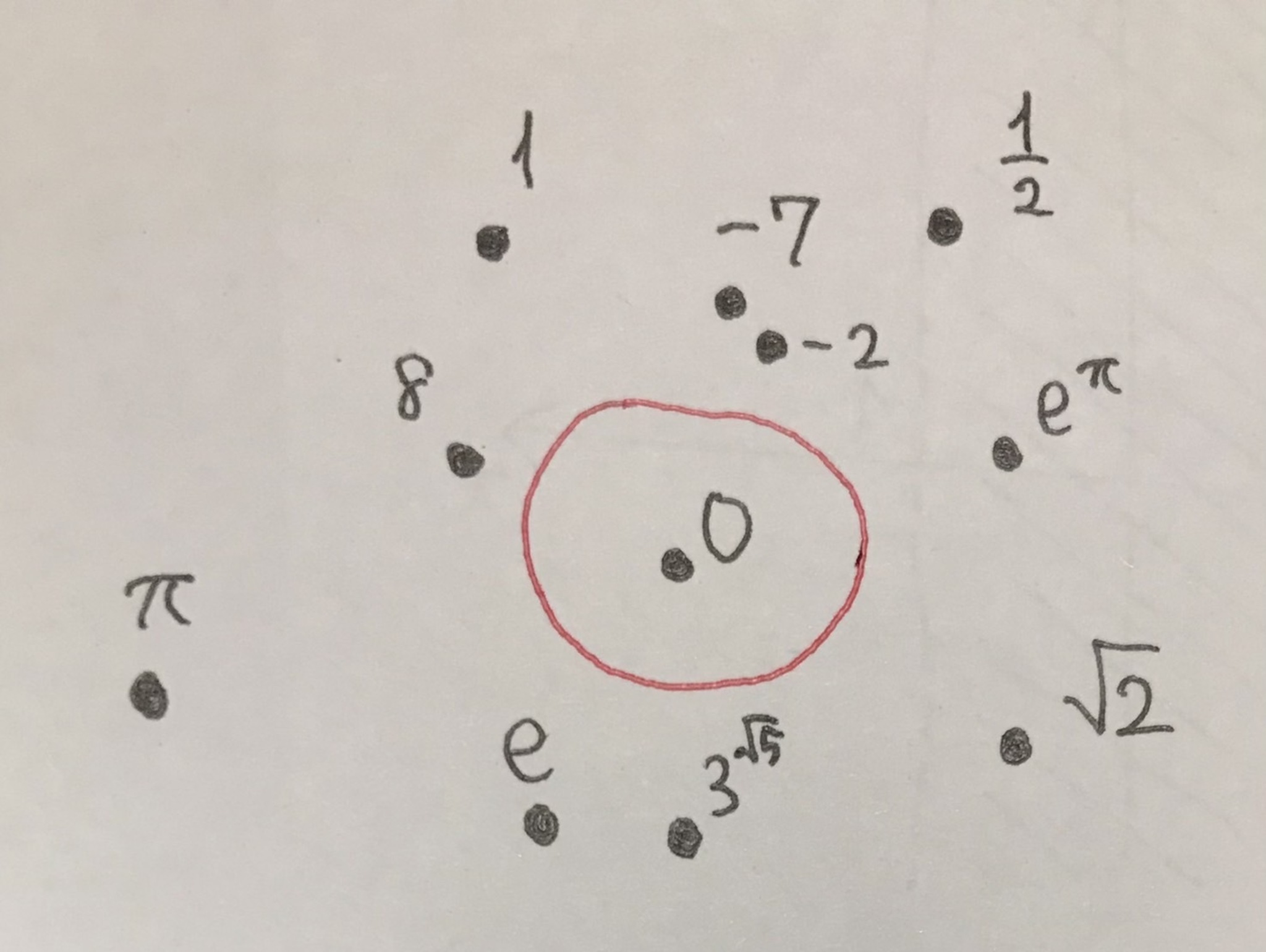0のみを囲んでいる輪っか
通常のユークリッド空間ではこうもいきません.
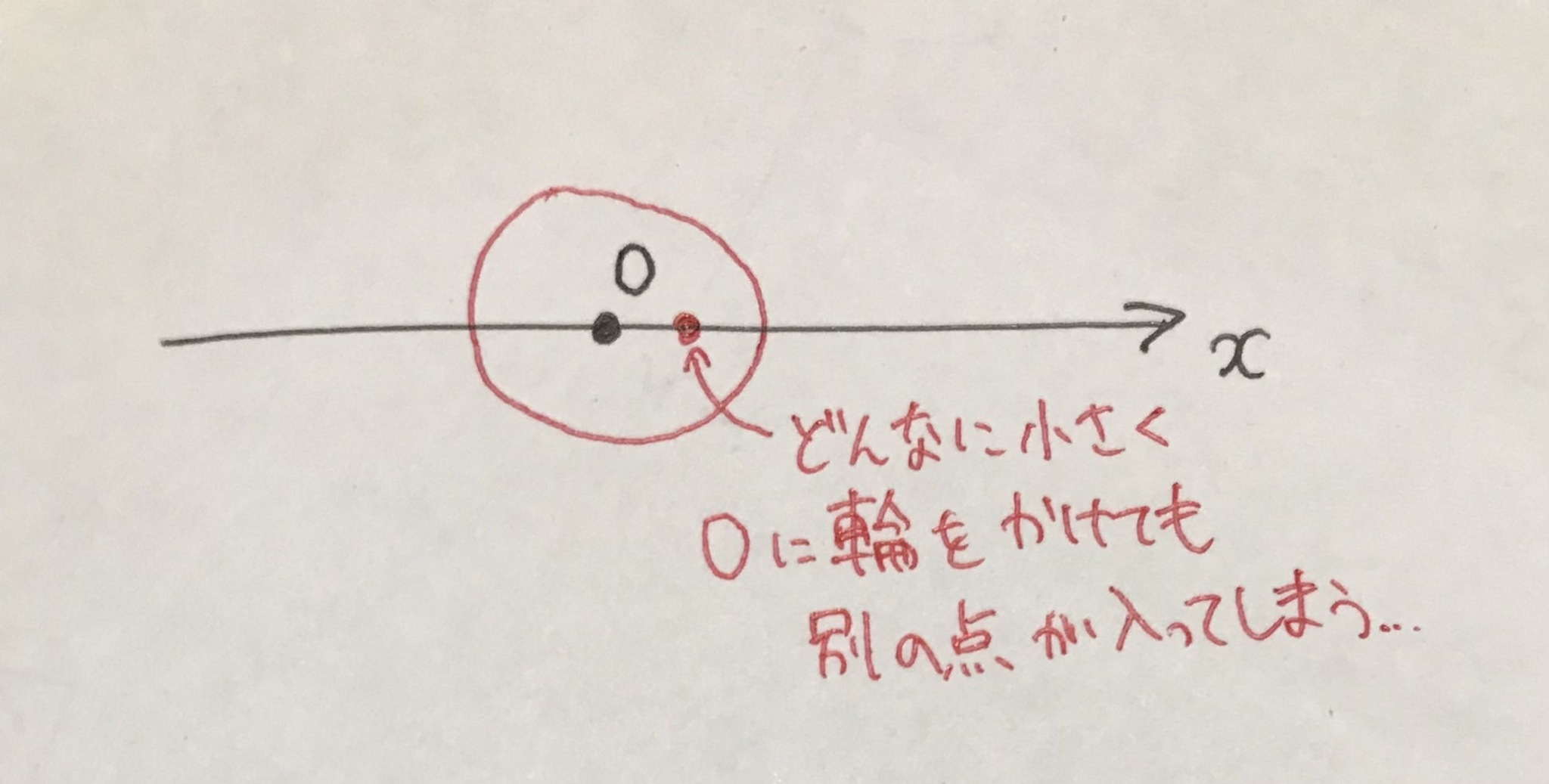0のみを囲むことはできない
離散位相ではどんな数$x \in \mathbb{R}$に対しても「$x$のみを囲む」ということがいつでもできます. こんなことができる空間...... それは「全部の点同士が離れて存在している空間」ではないでしょうか！！！！！ 点の近くに点が存在していれば, ユークリッド空間のように1点のみを囲もうとするとき近くの点も入ってきてしまうはずです. しかし離散位相ではそんな心配がいりません. もう離散のニュアンスを十分感じ取れたのではないでしょうか！！！！！
密着位相を解釈する
この調子で密着位相も解釈してしまいましょう！
$X$を空でない集合とするとき, 自分自身と空集合のみの集合$\{X,\emptyset\}$を開集合とする位相空間$(X,\{X,\emptyset\})$を密着位相という.
イメージしやすいよう, $\mathbb{R}$の密着位相$(\mathbb{R},\{\mathbb{R},\emptyset\})$で考えます.
$0$を囲む輪っかを描いてみます.
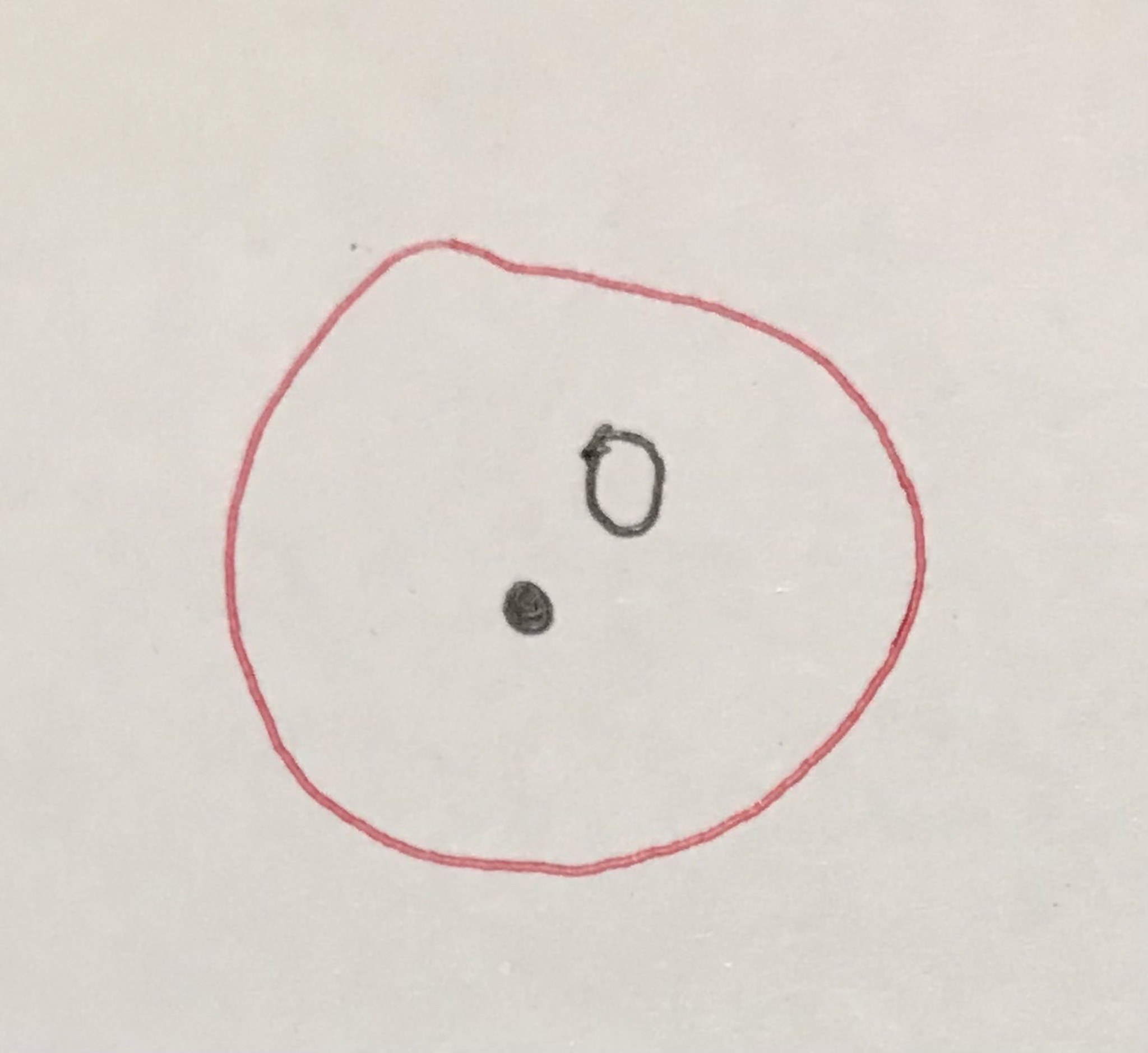0を囲んでみたが...？
さて, 密着位相の開集合は$\mathbb{R}$と$\emptyset$のみでした. 今回囲んだ範囲は$0$が入っているので空集合ではありません.
ということは今囲んだのは$\mathbb{R}$です. まじか.
どういうことだ...？ 今度は$1$を囲んでみます
画像いる？
密着位相の開集合は$\mathbb{R}$と$\emptyset$のみでした. 今回囲んだ範囲は$1$が入っているので空集合ではありません.
ということは今囲んだのも$\mathbb{R}$です. なんで.
ここに解釈を与えてみましょう. 「点を1つ囲もうとしたら全てを囲んでしまった」という不思議な現象が起きましたが, こう考えられないでしょうか.
「全部の点が同じ場所にある」
つまり密着しているということですね！！！！！！！！！！！！！！！！！！！！！！
位相の性質を見る
ここはある程度既習の人向けです. 飛ばしても大丈夫です. 位相空間の性質を考えるために考案された数々の性質と解釈を照らし合わせてみましょう.
$(X,\mathcal{O})$を位相空間とするとき, 開集合かつ閉集合であるものが$X$と$\emptyset$のみであるなら, $(X,\mathcal{O})$は連結であるという.
一応連結でない例を与えておきます. $A$を$x$座標が$0$でない$\mathbb{R}^2$の点全体とし, ここに$\mathbb{R}^2$の相対位相（通常の位相）を入れます. すると$x$座標が$0$より大きい$\mathbb{R}^2$の点全体はその相対位相の開集合であり, 閉集合でもあります. 中心で真っ二つの集合ですからね. 連結でないのも納得です.
2点以上からなる離散位相は連結ではありません. イメージ通りです. 離れてるんですから.
逆に, 密着位相は常に連結です. イメージ通りです. くっついてるんですから.
$(X,\mathcal{O})$を位相空間とするとき, 部分集合$A \subset X$が稠密な部分集合であるとは, $\overline{A} = X$ となることである.
これも解釈しておきます. $X$のどの点を取ってきても$A \subset X$の触点になってしまうということは, どんな$X$の点の近くにも$A$の点があるということです. 例は世界一有名な例（実数全体に対する有理数全体）があるので省きます.
離散位相$(X,2^X)$の稠密な部分集合は$X$のみです. イメージ通りです. 近くに点がないんですから.
逆に, 密着位相は空でない部分集合がすべて稠密です. イメージ通りです. 近くどころか全て同じ場所にあるんですから.
$(X,\mathcal{O})$を位相空間とする. $x,y\in X$が異なる2点であれば, $X$の開集合$U,V \in \mathcal{O}$で $(U \cap V = \emptyset)$であるものがあり$x\in U , y\in V$ とできる（異なる2点が開集合で分離できる）という性質をもつとき, $(X,\mathcal{O})$はハウスドルフ空間であるという.
2点以上からなる離散位相はハウスドルフです. イメージ通りです. 1点だけを分離することができるんですから.
逆に, 密着位相は常にハウスドルフではありません. イメージ通りです. 点を1つ囲んだら全部入ってきてしまうんですから.
$(X,\mathcal{O}_X),$$(Y,\mathcal{O}_Y)$を位相空間とする. $f:X \rightarrow Y$が連続写像であるとは, 任意の$Y$の開集合$O$に対して$f^{-1}(O)$が$X$の開集合となることである.
離散位相から飛ばす写像はすべて連続です. イメージ通りです. そもそも定義域が繋がってないので行った先の像が繋がってるとか関係ないです.
逆に, 密着位相から飛ばす写像は定値写像以外連続になりません. イメージ通りです. 同じ場所にあるはずの点からいろんな場所に飛んだらそりゃ連続と呼びたくないです.
まとめ
ここまで離散位相と密着位相に絞って位相空間を考えてきました. 開集合の多さ（？）が輪っかで囲む自由度を表していて, それが逆にどういう空間であるかの説明をしていたというわけです. 開集合を見ればどんな空間かがわかるという気がしてきました. 輪っかで囲む自由度はそのまま分離公理につながっていくテーマだと思うので, 少々強引な解釈ではありましたが考察の道具として使えるのではないでしょうか.
ここまで読んでいただきありがとうございました！！！！！！
それではさようなら～～～～～～～～
