ロドリゲスの回転公式

3次元の回転変換をベクトルで記述する、ロドリゲスの回転公式を紹介します。なお、この内容は先日開催された 第3回すうがく徒のつどい の「四元数と回転」で話した内容の一部です。その際の 講演資料 には画像がありませんでしたが、今回は画像を作成しました。

ロドリゲスの回転公式

以下、3次元ベクトル空間$\mathbb{R}^3$で考えます。ベクトル$\vec{x}$と$\vec{y}$の内積を$\langle\vec{x}|\vec{y}\rangle$と、外積を$\vec{x}\times\vec{y}$と書くことにします。

3次元空間のなかで、原点を通る回転軸の周りに回転角$\theta$だけ回転するという変換は、次のように記述できます。

$\vec{n}$は回転軸に沿う単位ベクトルです。$\vec{n}$の周りに角$\theta$だけ回転するという操作を図で示すと、次のようになります。

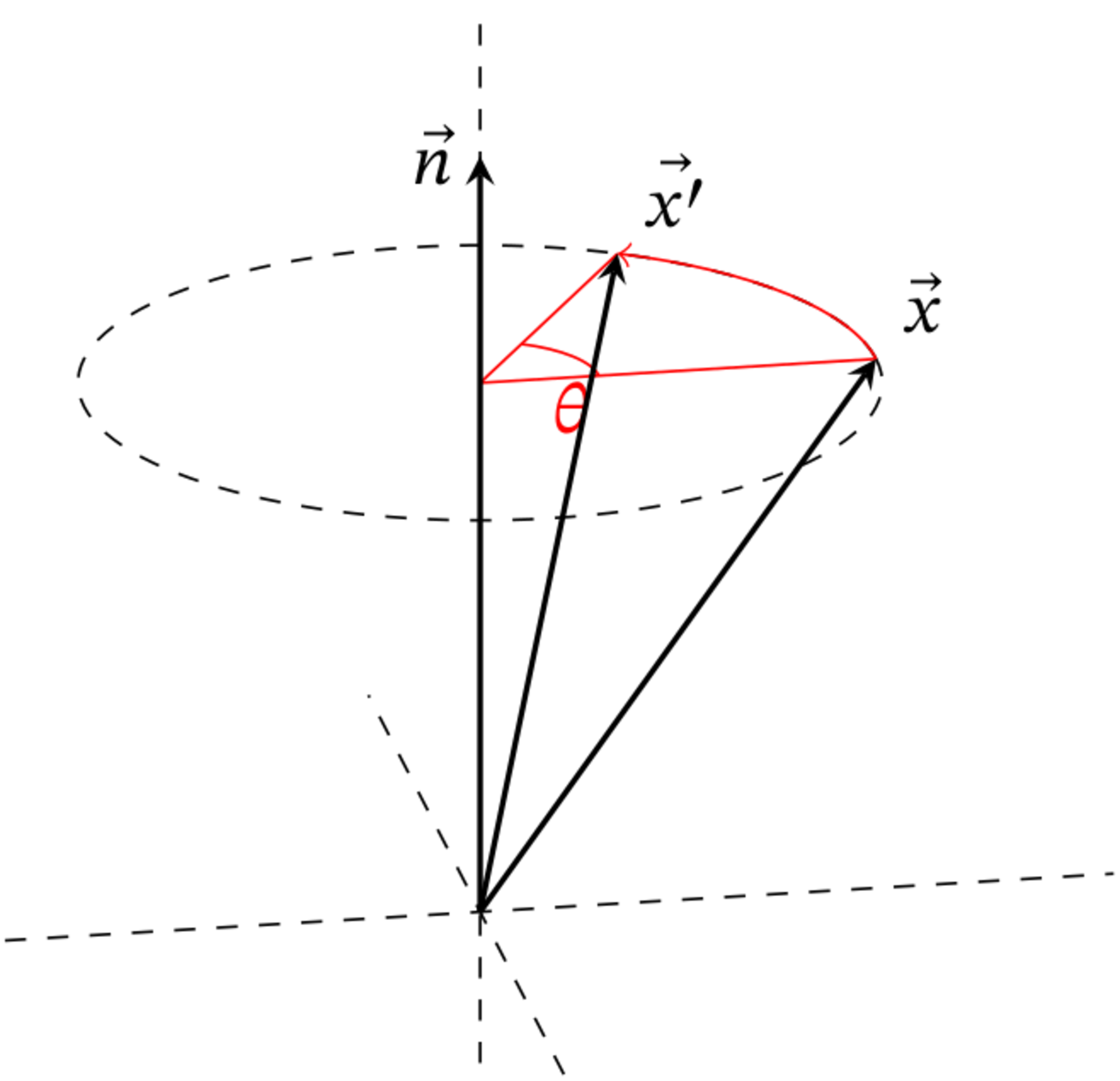回転軸の周りの回転

ロドリゲスの回転公式は、回転後のベクトル$\vec{x'}$を、$\vec{x}$、$\vec{n}$、$\vec{n}\times\vec{x}$の3つのベクトルの和の形で記述しています。

ロドリゲスの回転公式の証明

以下、ロドリゲスの回転公式を証明します。

まず、$\vec{x}$を$\vec{n}$と平行な方向$\vec{x}_\parallel$と垂直な方向$\vec{x}_\perp$に分解します。
\begin{equation} \vec{x}=\vec{x}_\parallel+\vec{x}_\perp \end{equation}
このとき、$\vec{x}_\parallel=\langle\vec{n}|\vec{x}\rangle\vec{n}$となります。

$\vec{x'}$も同様に分解します。
\begin{equation} \vec{x'}=\vec{x'}_\parallel+\vec{x'}_\perp \end{equation}
このとき、点$X'$は点$X$を$\vec{n}$の周りに回転した点であることから、$\vec{x}$と$\vec{x'}$について、$\vec{n}$と平行な方向の成分は等しくなります。つまり$\vec{x'}_\parallel=\vec{x}_\parallel$です。

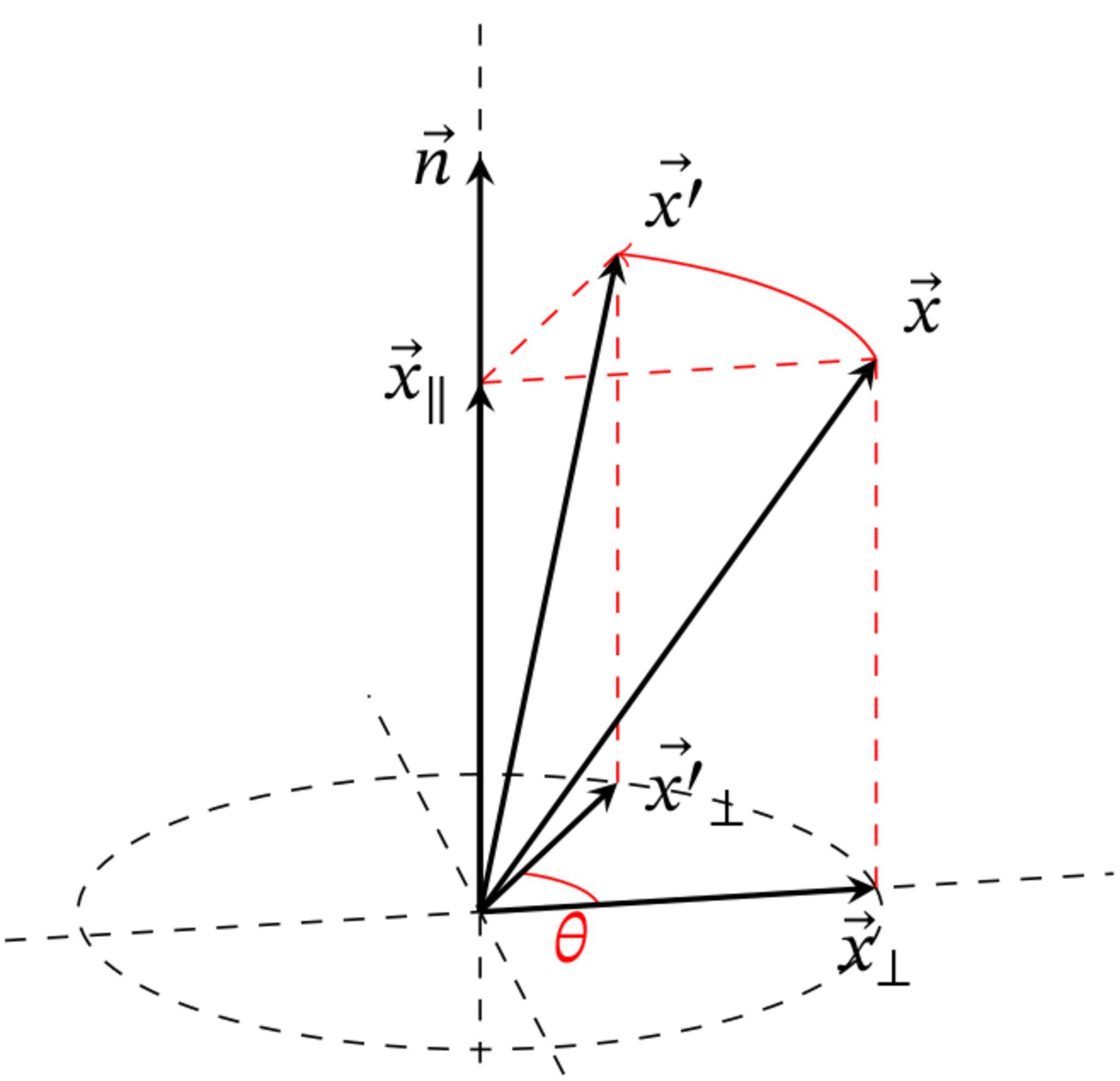位置ベクトルの分解

よって、$\vec{x'}_\parallel$は$\vec{x}$と$\vec{n}$であらわせることが分かりました。次に、$\vec{x'}_\perp$を$\vec{x}$と$\vec{n}$であらわすことを考えます。

外積$\vec{n}\times\vec{x}_\perp$を考えます。外積の大きさは平行四辺形の面積でしたから、これは実は$\vec{n}\times\vec{x}$と等しいです。

$\vec{n}$と$\vec{x}_\perp$は直交していることから、次が成り立ちます。
\begin{equation} |\vec{n}\times\vec{x}_\perp|=|\vec{n}||\vec{x}_\perp|\sin\frac{\pi}{2}=|\vec{n}||\vec{x}_\perp|=|\vec{x}_\perp| \end{equation}
よって、$\vec{x}_\perp$、$\vec{x'}_\perp$、$\vec{n}\times\vec{x}_\perp$はすべて同じ大きさです。

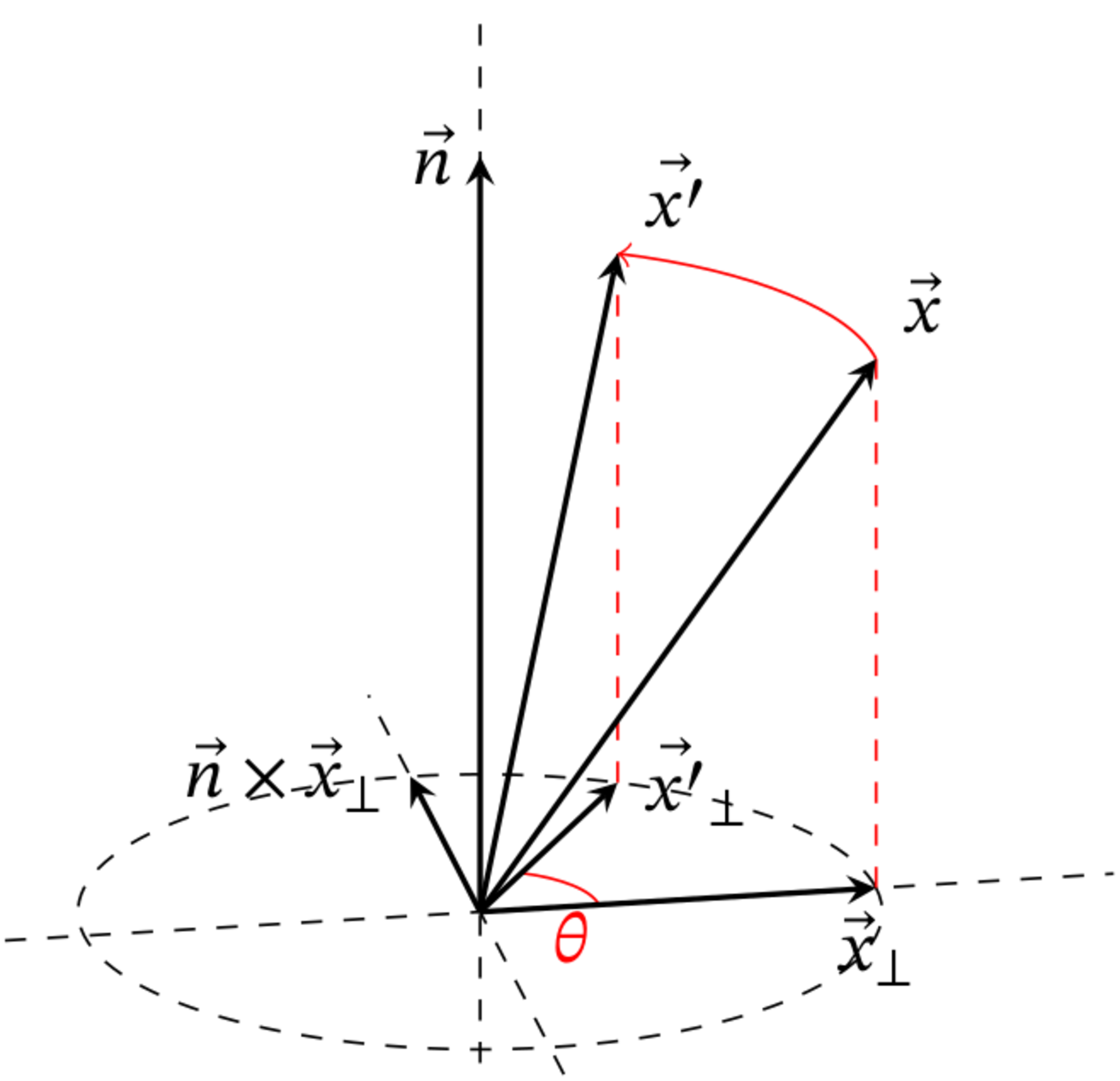外積ベクトル

$\vec{x'}_\perp$を$\vec{x}_\perp$方向と$\vec{n}\times\vec{x}_\perp$方向に分解します。
$\vec{x}_\perp$と$\vec{x'}_\perp$のなす角は$\theta$なので、次のようになります。
\begin{equation} \vec{x'}_\perp=\cos\theta\vec{x}_\perp+\sin\theta(\vec{n}\times\vec{x}_\perp) \end{equation}

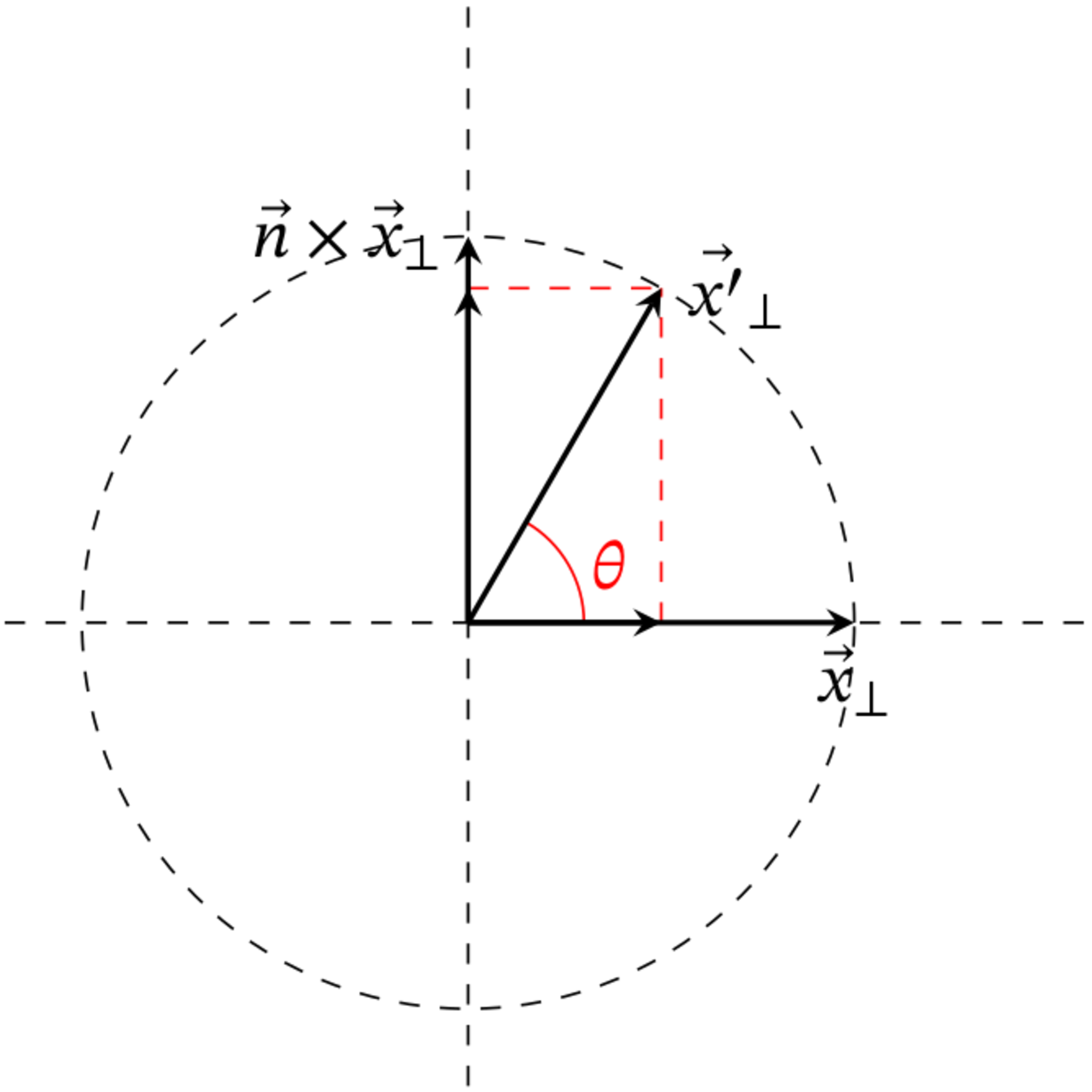ベクトルの分解

これで、$\vec{x'}_\perp$を$\vec{x}$と$\vec{n}$であらわすことができました。したがって、次が成り立ちます。
\begin{align} \vec{x'} & =\vec{x'}_\parallel+\vec{x'}_\perp \\ & =\vec{x}_\parallel+\cos\theta\vec{x}_\perp+\sin\theta(\vec{n}\times\vec{x}_\perp) \\ & =\vec{x}_\parallel+\cos\theta(\vec{x}-\vec{x}_\parallel)+\sin\theta(\vec{n}\times\vec{x}) \\ & =\cos\theta\vec{x}+(1-\cos\theta)\vec{x}_\parallel+\sin\theta(\vec{n}\times\vec{x}) \\ & =\cos\theta\vec{x}+(1-\cos\theta)\langle\vec{n}|\vec{x}\rangle\vec{n}+\sin\theta(\vec{n}\times\vec{x}) \end{align}

以上でロドリゲスの回転公式が証明できました。