3
競技数学解説
匿式図形問題エスパー杯 The 2nd (T-GUESS Cup 2) 問題Ａ～Ｃの解説
199
0
$$$$
先日開催した
匿式図形問題エスパー杯 The 2nd
(Tock's Geometry "Using Extra-Sensory Solutions" Cup - The 2nd)、通称T-GUESS Cup 2の問題を解説する。どの問題も決して簡単ではなかったと推察するが、まずはそれぞれの問題を紹介しよう。目次の通り、問題紹介のすぐ後に解答を記載しているので、もしも自力で解きたい読者がいらっしゃればその直前でスクロールを停止していただきたい。
問題Ａ
1辺が$2$である正方形$ABCD$の内部に$BE=2$をみたす点$E$をとり、点$D$について点$E$と対称な点を$F$とすると、$BE \parallel CF$が成立した。$CF$の長さを求めよ。
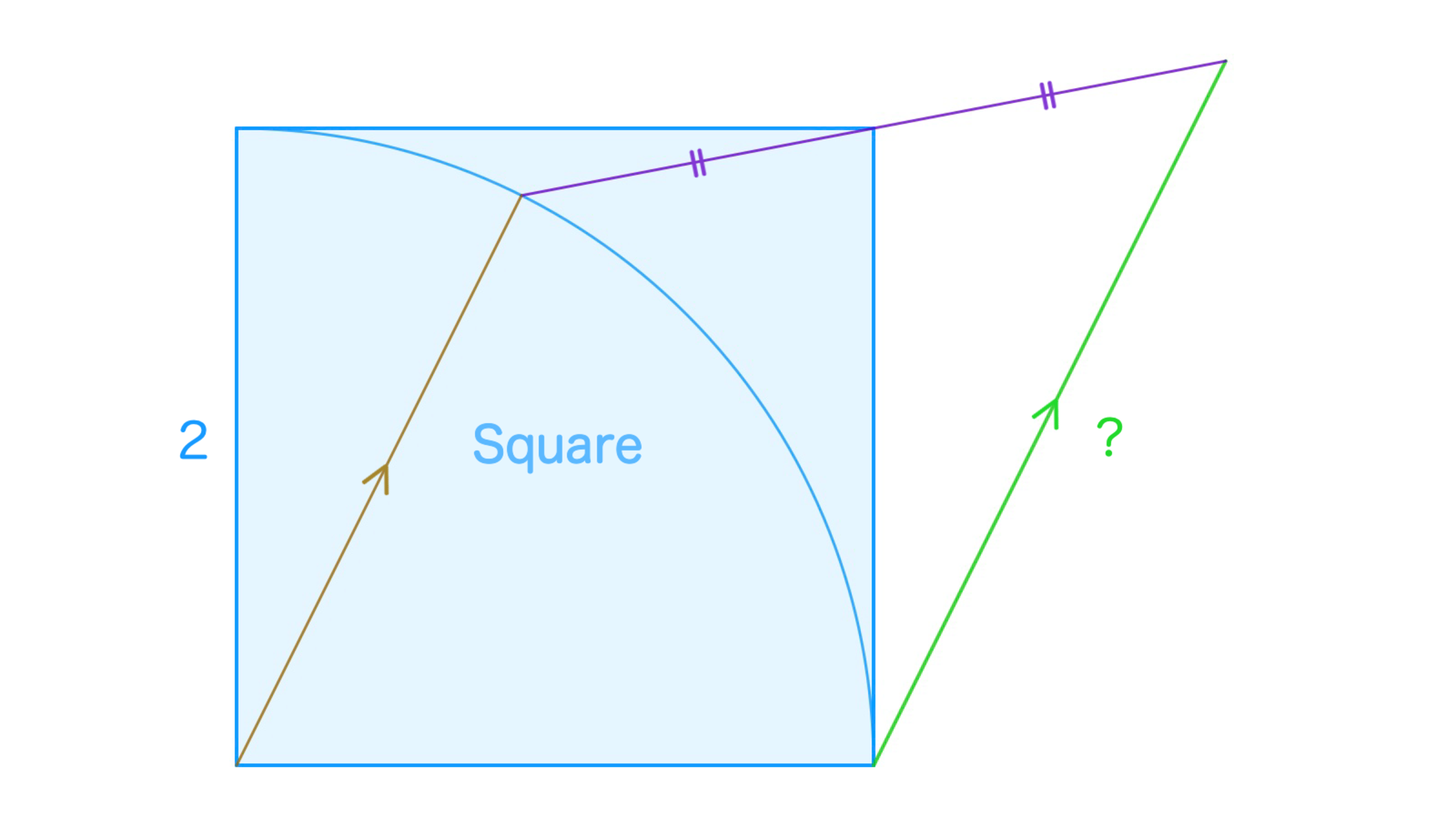数オリの予選でも最初か2問目くらいに出題されそう
問題Ｂ
三角形$ABC$において、$\angle A$内の傍心を$J$とし、線分$AJ$を直径とする円と半直線$JC$の交点を$D(\neq J)$とする。$AC$と$BD$の交点を$P$とすれば$\triangle ABP=22,$ $\triangle CDP=7$となるとき、$\triangle BCP$の面積を求めよ。
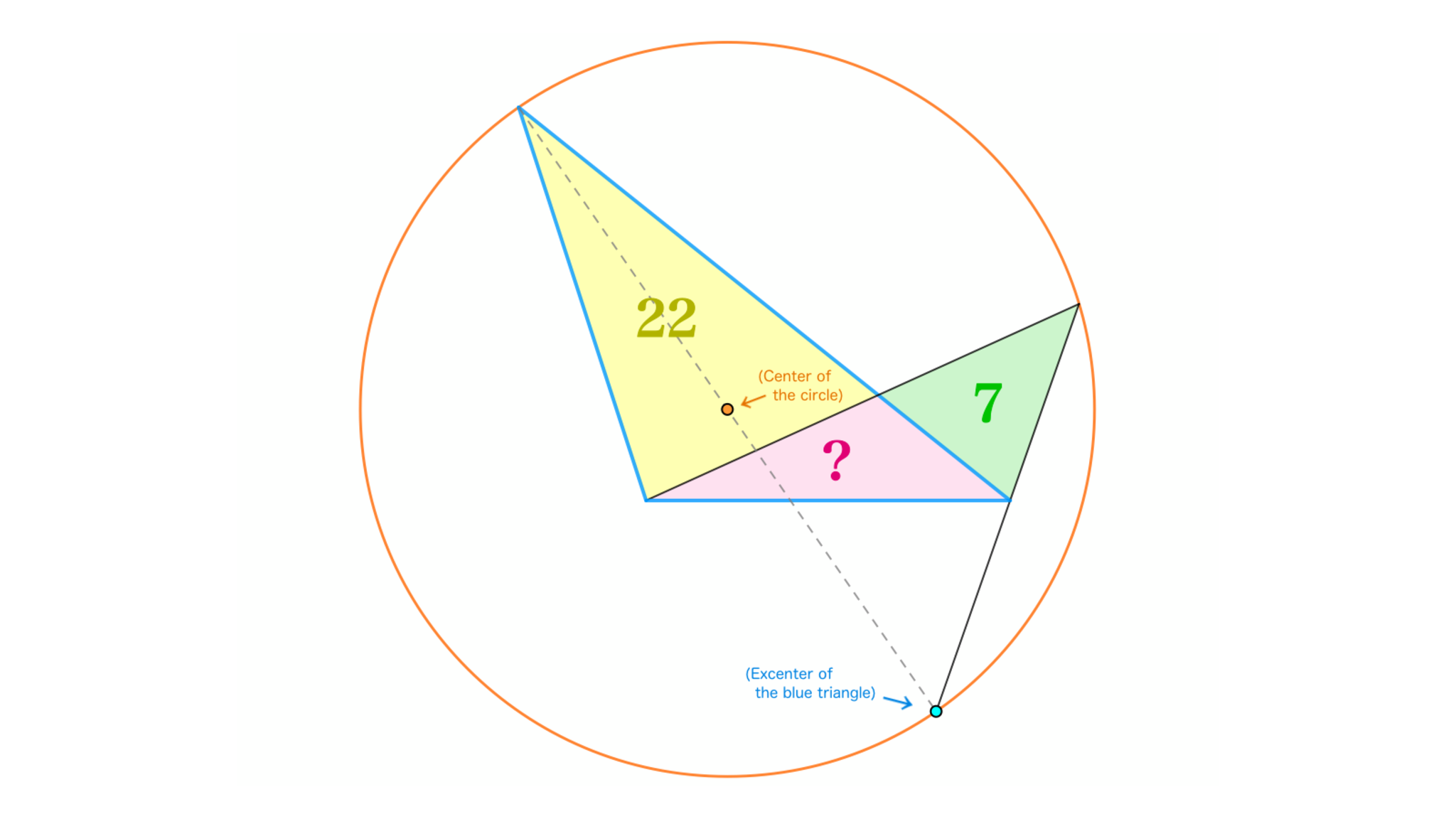そういえば22/7って円周率の近似値なんですよね
問題Ｃ
長方形$ABCD$の辺$AB$上に点$E$、辺$AD$上に点$F$をとる。$EF$を折り目として長方形$ABCD$を折ると、点$A$は辺$BC$上の点$P$に移った。線分$DF$上の点$Q$が$DQ=7,$ $FQ=9$をみたし、3直線$AC,EQ,FP$が1点で交わるとき、$AF$の長さを求めよ。
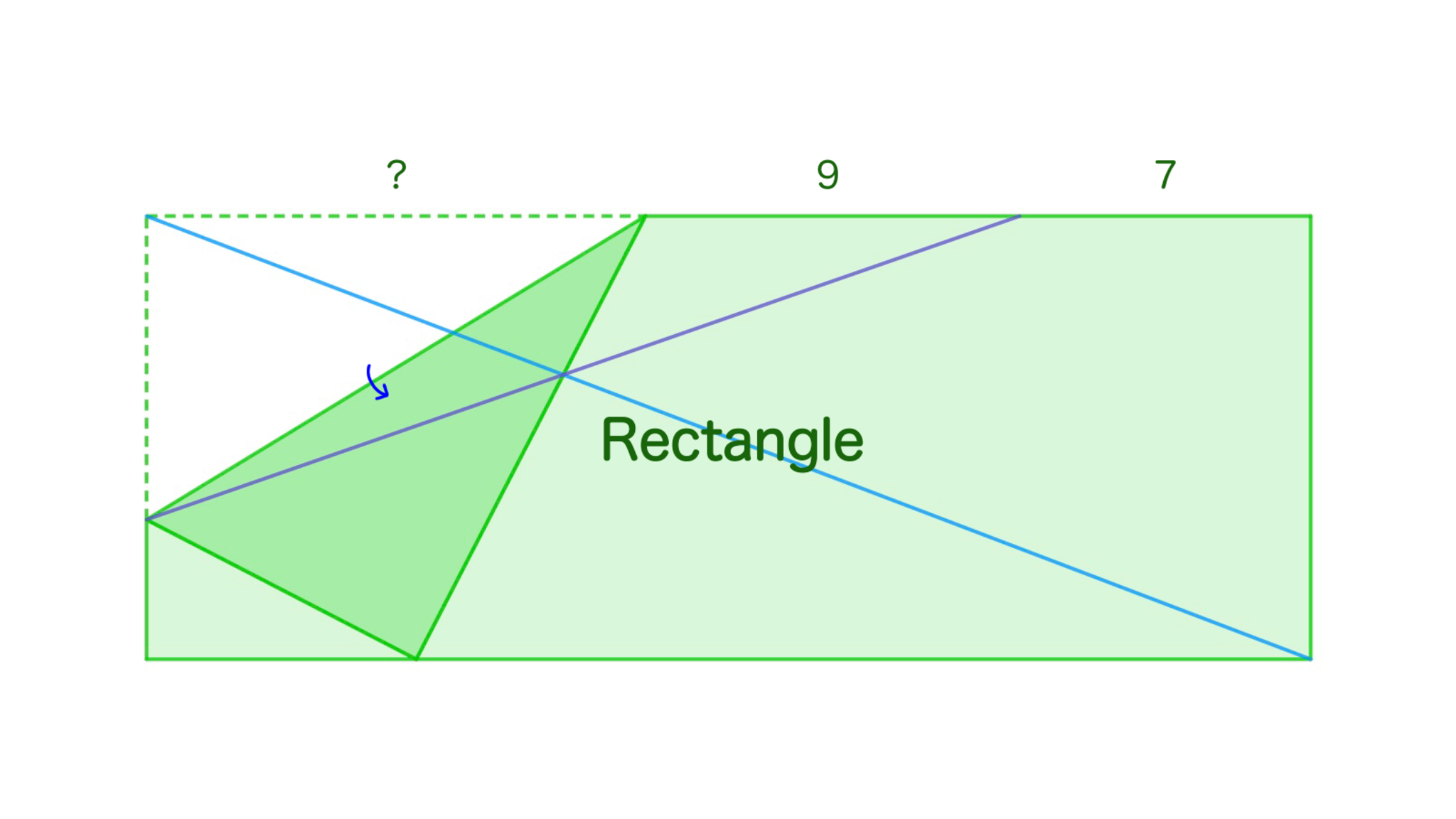本当に条件が足りているか疑わしい
問題Ｄ
五角形$ABCDE$は$AB=CD=DE$をみたす。辺$BC$上に2点$F,G$をとると、4点$B,F,G,C$はこの順に並び、$BF=CG$が成立した。$\angle CAE=\angle ACD=41^{\circ},$ $\angle CDF=\angle EDF=82^{\circ},$ $\angle BAC=57^{\circ}$のとき、直線$AG$と直線$DF$のなす角(のうち$90^{\circ}$以上$180^{\circ}$未満であるもの)を求めよ。
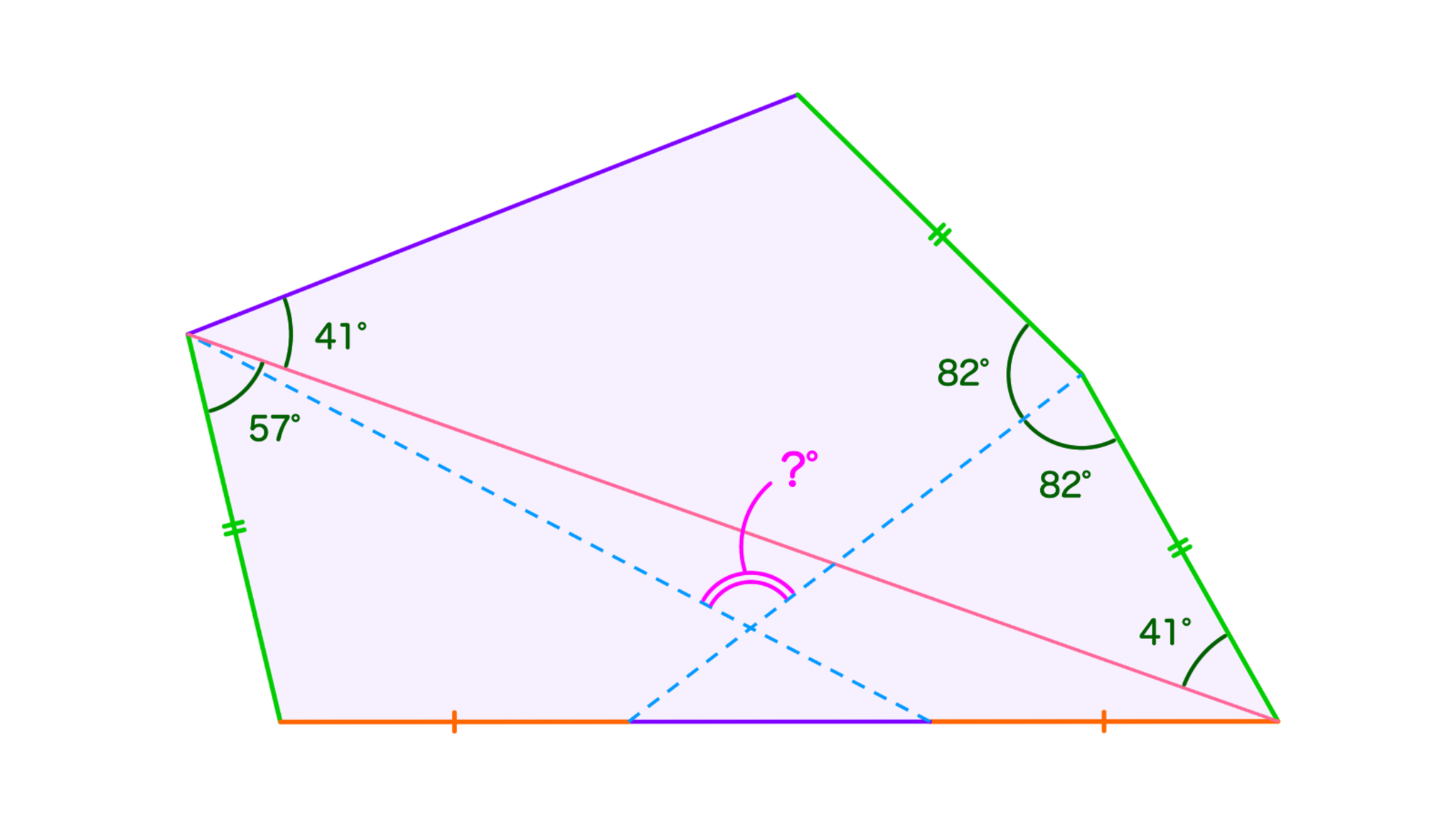そもそも図を描くのが難しい
解答
| 問題Ａ | 問題Ｂ | 問題Ｃ | 問題Ｄ |
|---|---|---|---|
| $2\sqrt{5}-2$ | $8$ | $12$ | $115^{\circ}$ |
以下で問題Ａ～Ｃの解説をする。問題Ｄの解説は長くなるので、別の記事に掲載する。
問題Ａの解説
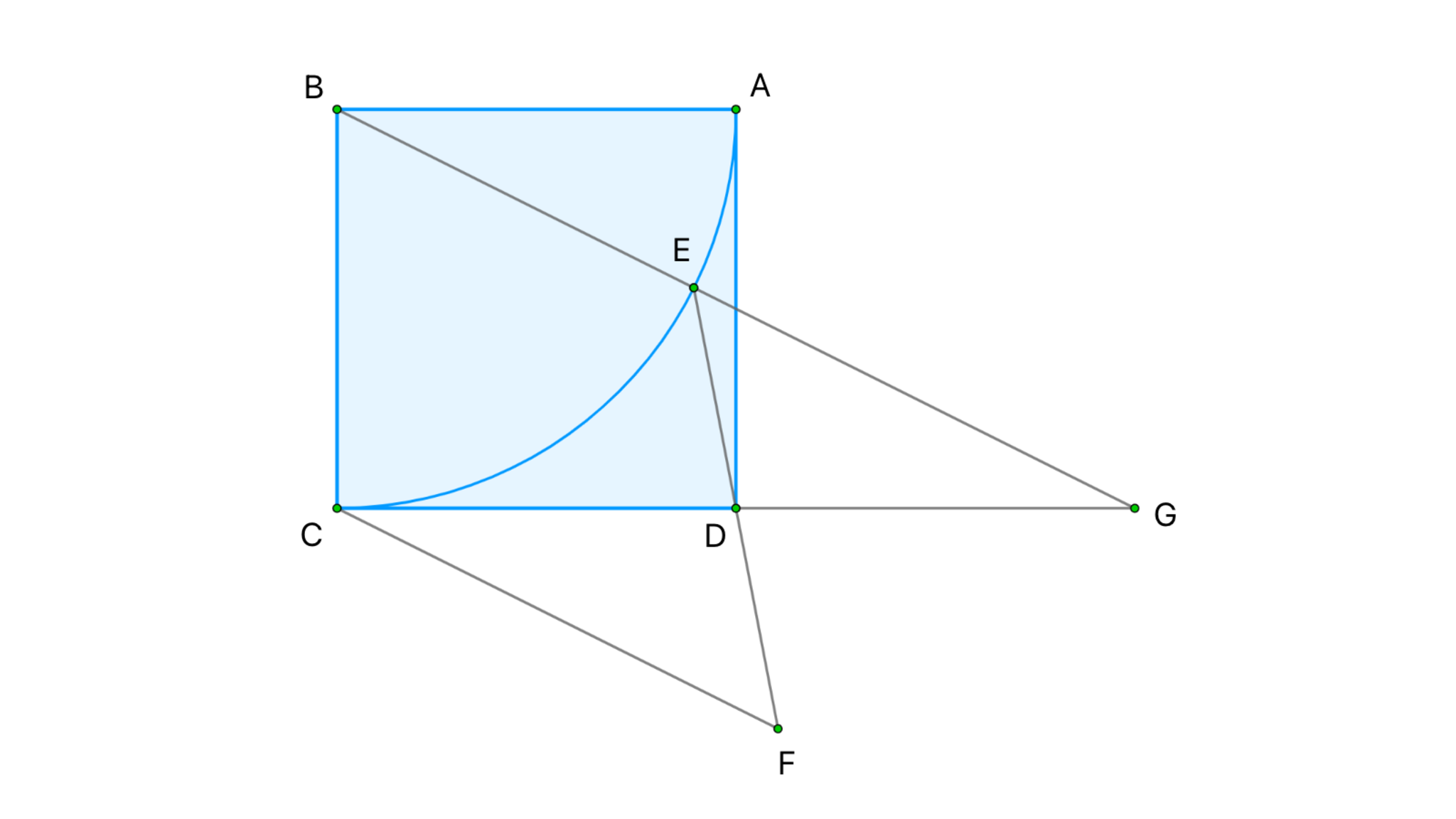シンプルイズベスト、ベストイズシンプル
点$D$について点$C$と対称な点を$G$とすると、明らかに$DE=DF,$ $DC=DG,$ $\angle CDF=\angle GDE$となり、2辺とその間の角がそれぞれ等しいので$\triangle CDF \equiv \triangle GDE$である。したがって$\angle DEB+\angle DEG$$=\angle DEB+\angle DFC=180^{\circ}$$(\because BE \parallel CF)$であるから、3点$B,E,G$はこの順で同一直線上にある。
したがって$CF=GE$$=BG-BE$$=\sqrt{BC^2+CG^2}-BE=$$2\sqrt{5}-2$を得る。
したがって$CF=GE$$=BG-BE$$=\sqrt{BC^2+CG^2}-BE=$$2\sqrt{5}-2$を得る。
問題Ｂの解説
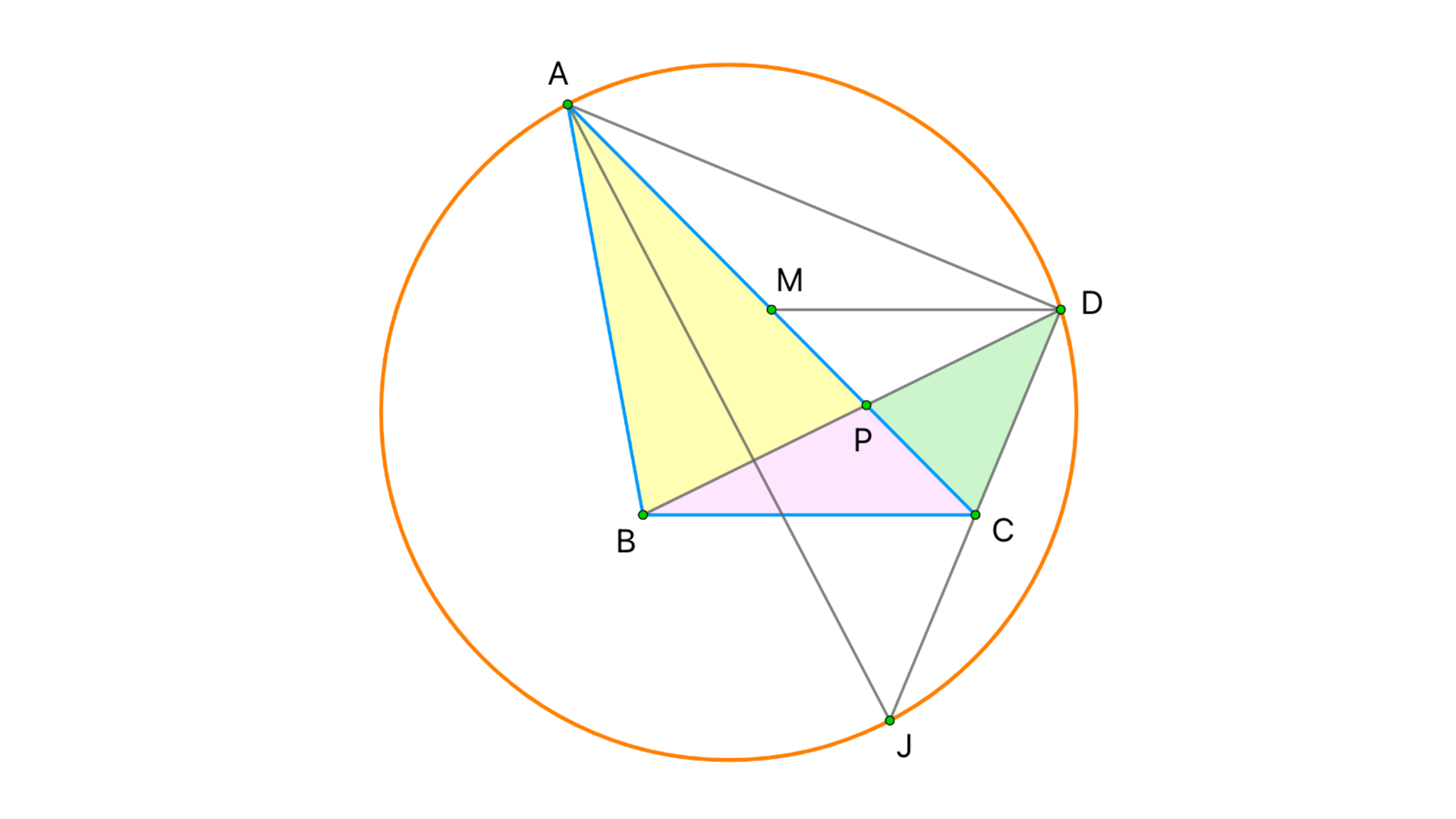どの辺の長さも求めなくてよい(というか求められない)問題
辺$AC$の中点を$M$とする。線分$AJ$は円の直径であったから、円周角の定理(もしくはタレスの定理)より$\angle ADJ=90^{\circ}$と判る。すなわち$\triangle ADC$は直角三角形であり、特に点$M$は$\triangle ADC$の外心となる($\because$点$M$は斜辺の中点)。点$J$は$\triangle ABC$の傍心なので$\angle BCJ=\angle ACD$が成り立ち、$MC=MD$から$\angle MCD=\angle MDC$を得るので、これらを統合して$\angle BCJ=\angle MDJ$、つまり$BC \parallel MD$が導かれる。
したがって$\triangle BCD=\triangle BCM$$=\dfrac{\triangle ABC}{2}$となり、面積を計算することで$\triangle BCP+22$$=2(\triangle BCP+7)$、ゆえに$\triangle BCP=$$8$と示される。
したがって$\triangle BCD=\triangle BCM$$=\dfrac{\triangle ABC}{2}$となり、面積を計算することで$\triangle BCP+22$$=2(\triangle BCP+7)$、ゆえに$\triangle BCP=$$8$と示される。
問題Ｃの解説
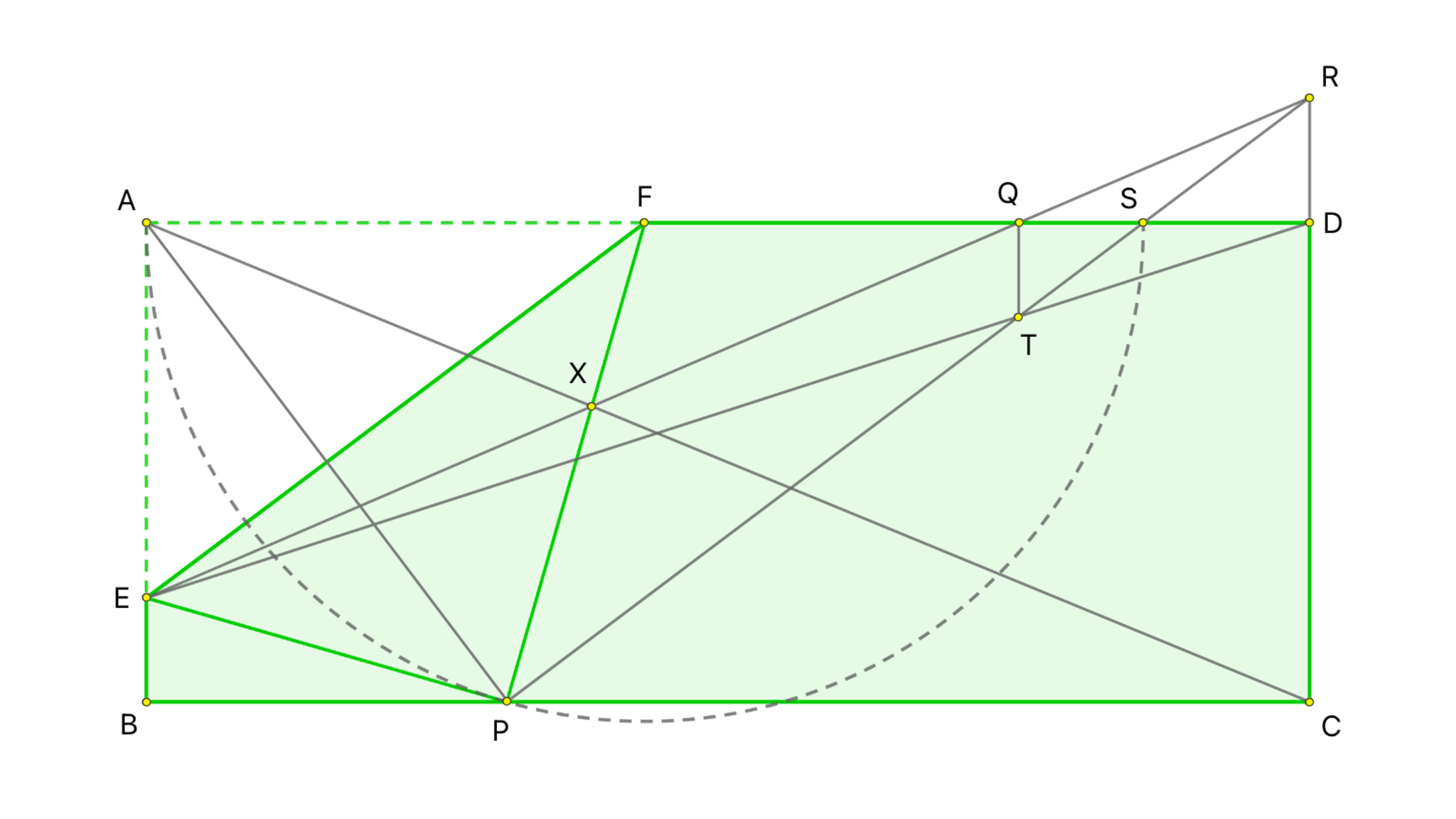正解者全員が想定解より簡潔に解いてきたという噂
3直線$AC,EQ,FP$が交わる点を$X$とし、$P$から引いた$EF$の平行線と半直線$CD$の交点を$R$とする。また、点$F$を中心とする半径$AF$の半円を描き、線分$DF$との共有点を$S$とする。このとき、$AE \parallel CR,$ $EF \parallel RP,$ $FA \parallel PC$より、3つの角がそれぞれ等しいので$\triangle AEF \sim \triangle CRP$が従い、特に点$X$はこの相似の中心となっている。すなわち4点$E,X,Q,R$はこの順で同一直線上に存在する。
円周角の定理より$\angle ASP=\dfrac{\angle AFP}{2}=\angle AFE$であり、ここから$EF \parallel PS$を得るので、3点$P,S,R$はこの順で同一直線上に存在する。$DE$と$PR$の交点を$T$とすると、長さの比を計算して、
円周角の定理より$\angle ASP=\dfrac{\angle AFP}{2}=\angle AFE$であり、ここから$EF \parallel PS$を得るので、3点$P,S,R$はこの順で同一直線上に存在する。$DE$と$PR$の交点を$T$とすると、長さの比を計算して、
$$DT:TE=DS:SF=DS:AF=DR:AE=DQ:QA$$
が判る。よって$AE \parallel QT$となり、3つの角がそれぞれ等しいので$\triangle AEF \sim \triangle QTS$が導かれる。この相似の中心は明らかに点$D$であるから、$AF:FD=QS:SD$より$AF:16$$=(AF-9):(16-AF)$を得て、これを解くと$AF=$$12$を得る。
主催者コメント
良問揃いである。繰り返す。良問揃いである。さらに繰り返す。良問揃いである。誰が何と言おうとも、良問揃いである。どうか良問揃いであると認めていただきたい。これでも作問に4ヶ月程度を費やしているのだ。およそ40問の候補の中から厳選したセットなのだ。頼むから良問と言ってくれ。無理か。無理なのか。そこを何とか。
投稿日：2022年5月8日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中