1
競技数学解説
匿式図形問題エスパー杯 The 2nd (T-GUESS Cup 2) 問題Ｄの解説
110
0
$$$$
問題
五角形$ABCDE$は$AB=CD=DE$をみたす。辺$BC$上に2点$F,G$をとると、4点$B,F,G,C$はこの順に並び、$BF=CG$が成立した。$\angle CAE=\angle ACD=41^{\circ},$ $\angle CDF=\angle EDF=82^{\circ},$ $\angle BAC=57^{\circ}$のとき、直線$AG$と直線$DF$のなす角(のうち$90^{\circ}$以上$180^{\circ}$未満であるもの)を求めよ。
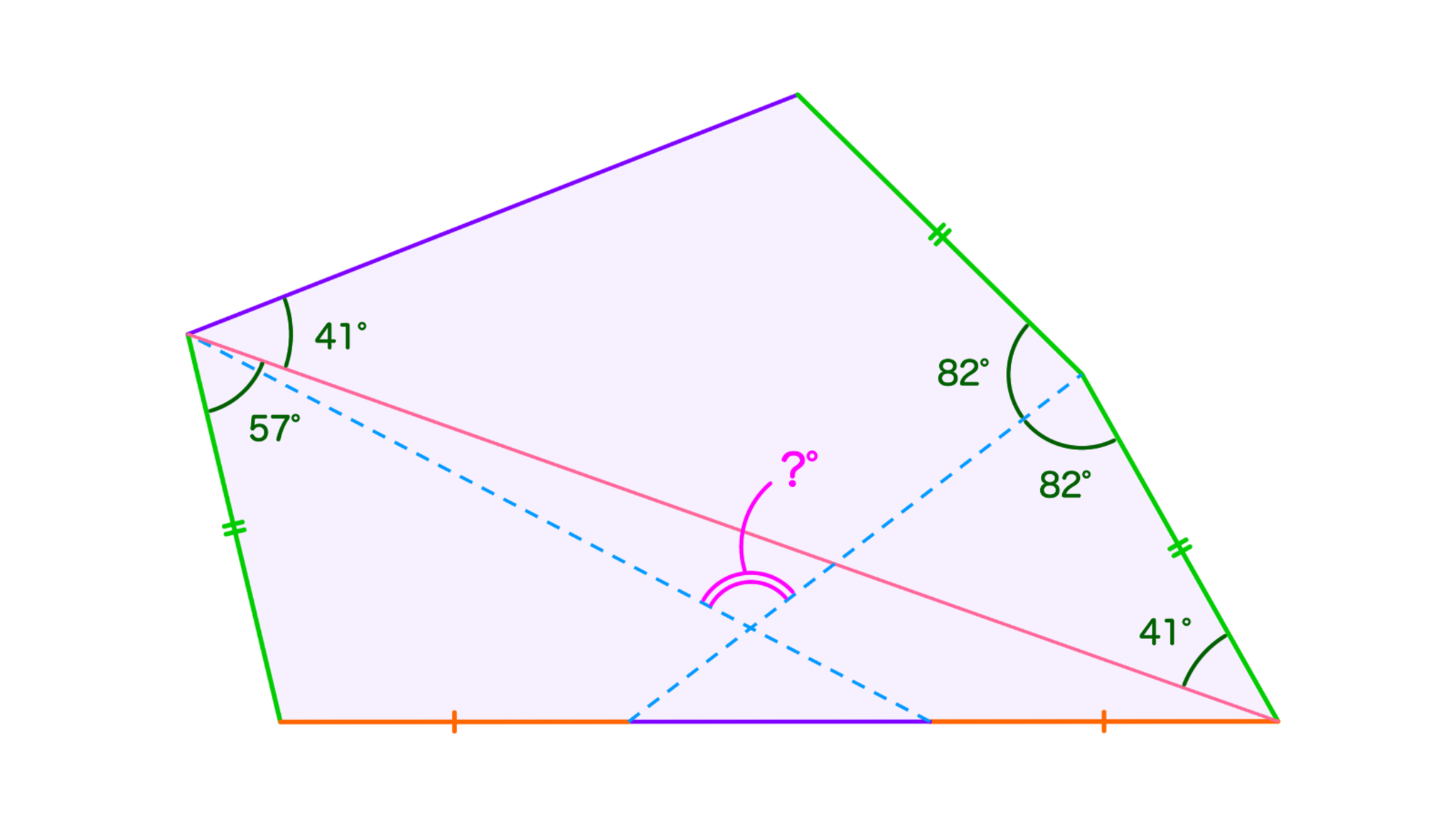見るからに難しそうな問題
求角問題を1度でも解いたことがある人であれば、「え、多分無理数になるよね、その角度」と思われるだろう。しかし、何故か有理数になる。我ながら少々不思議に感じていたりいなかったり。
さあ、証明しよう……と行きたいところだが、正直なところ解説を読むためにある程度体力が必要だと思われるので、もしも体力に自信のない読者がいらっしゃれば校庭10周とスクワット500回をしてから読み進めることを推奨する。
さあ、証明しよう……と行きたいところだが、正直なところ解説を読むためにある程度体力が必要だと思われるので、もしも体力に自信のない読者がいらっしゃれば校庭10周とスクワット500回をしてから読み進めることを推奨する。
用意していた解説
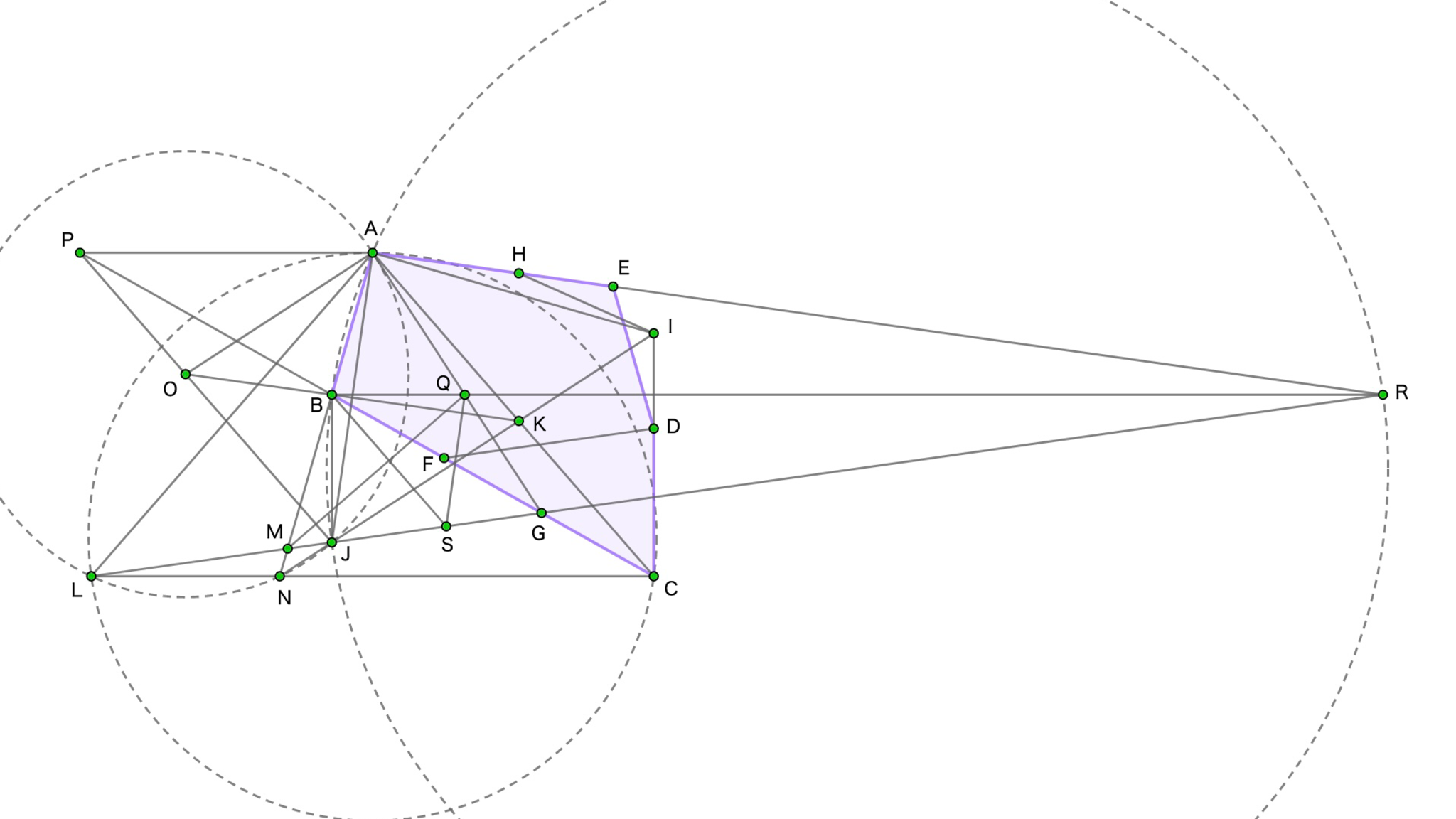点Rが遠すぎる
辺$AE$上に$AH=CD$をみたす点$H$を、半直線$CD$上に$AE=CI$をみたす点$I$をとると、四角形$ACDE$と四角形$AHIC$は合同である(線分$AC$の垂直二等分線について四角形$ACDE$を対称移動させるイメージ)。また$BG=CF$より、$\triangle CFD \equiv \triangle BGJ$となるような点$J$をとることができる。
$\triangle ABJ$と$\triangle AHI$について、$AB=CD=AH,$ $BJ=CD=DE=HI,$ $\angle ABJ=\angle ABG+\angle JBG$$=\angle ABG+\angle DCF=164^{\circ}$ ($\because$五角形の内角の和は$540^{\circ}$)$,$ $\angle AHI=\angle CDE=164^{\circ}$より、2辺とその間の角がそれぞれ等しいので$\triangle ABJ \equiv \triangle AHI$が成り立っている。ゆえに$\triangle AIJ$は二等辺三角形であり、$\angle IAJ$$=\angle BAH-\angle BAJ-\angle HAI=82^{\circ}$とわかる。$AC$と$IJ$の交点を$K$とすると、$\angle JAK=\angle BAK-\angle BAJ=49^{\circ},$ $\angle AJK=\dfrac{180^{\circ}-\angle IAJ}{2}=49^{\circ}$なので、$\triangle JAK$も$AK=JK$の二等辺三角形になっている。
$\triangle ABJ$と$\triangle AHI$について、$AB=CD=AH,$ $BJ=CD=DE=HI,$ $\angle ABJ=\angle ABG+\angle JBG$$=\angle ABG+\angle DCF=164^{\circ}$ ($\because$五角形の内角の和は$540^{\circ}$)$,$ $\angle AHI=\angle CDE=164^{\circ}$より、2辺とその間の角がそれぞれ等しいので$\triangle ABJ \equiv \triangle AHI$が成り立っている。ゆえに$\triangle AIJ$は二等辺三角形であり、$\angle IAJ$$=\angle BAH-\angle BAJ-\angle HAI=82^{\circ}$とわかる。$AC$と$IJ$の交点を$K$とすると、$\angle JAK=\angle BAK-\angle BAJ=49^{\circ},$ $\angle AJK=\dfrac{180^{\circ}-\angle IAJ}{2}=49^{\circ}$なので、$\triangle JAK$も$AK=JK$の二等辺三角形になっている。
$AI=AJ$より、$\triangle ACI \equiv \triangle ALJ$となるような点$L$をとることができる。$\angle AJL=\angle AIC$$=\angle HIC-\angle HIA=106^{\circ},$ $\angle AJG=\angle BJG-\angle BJA=74^{\circ}$であるから$\angle AJL+\angle AJG=180^{\circ}$となり、3点$L,J,G$はこの順で同一直線上にあると判明する。なお、$AC=AL,$ $\angle CAL=\angle CAJ+\angle JAL$$=\angle IAC+\angle CAJ$$=\angle IAJ$であるため、$\triangle ACL \sim \triangle AIJ$となることに注意する。ここで半直線$AB$と$GL,CL$の交点をそれぞれ$M,N$とすると、$\angle JAN=\angle JAB=8^{\circ},$ $\angle JLN=\angle ALC-\angle ALJ$ $=\angle AJI-\angle ACI=8^{\circ}$より、円周角の定理の逆を用いると4点$A,J,N,L$が同一円周上に存在するといえる。加えて、$\angle AJN=180^{\circ}-\angle ALN$$=180^{\circ}-\angle AJI$から$\angle AJI+\angle AJN=180^{\circ}$となり、3点$N,J,I$はこの順で同一直線上にある。
四角形$AJNL$の外接円の中心を$O$とすると、$\angle AOJ=2\angle ALJ=82^{\circ},$ $AO=JO$より、$\angle OAJ=\angle OJA=49^{\circ}$となる。$\triangle AJK$と$\triangle AJO$について、$AJ=AJ,$ $\angle AJK=\angle JAK$$=\angle AJO$$=\angle JAO=49^{\circ}$であり、1辺とその両端の角がそれぞれ等しいので$\triangle AJK \equiv \triangle AJO$が成り立つ。すなわち四角形$AKJO$はひし形であり、$AB=JB$から点$B$は対角線$KO$上に存在する。
いま、$A$から引いた$CL$の平行線と$JO$との交点を$P$とすると、$AO \parallel NK,$ $OP \parallel KC,$ $PA \parallel CN$から、2つの角がそれぞれ等しいので$\triangle AOP \sim \triangle NKC$となる。それから、$AO \parallel NK$は$\triangle AOB \sim \triangle NKB$であることも表している。これら2つの相似から$AB:NB$$=AO:NK$$=AP:NC$が判り、$\angle BAP=\angle BNC$($\because$平行線の錯角)と併せて、2辺の比とその間の角がそれぞれ等しいので$\triangle ABP \sim \triangle NBC$が成立する。ゆえに$\angle ABP=\angle NBC$であり、対頂角が等しいので3点$P,B,C$はこの順で同一直線上に存在する。
いま、$A$から引いた$CL$の平行線と$JO$との交点を$P$とすると、$AO \parallel NK,$ $OP \parallel KC,$ $PA \parallel CN$から、2つの角がそれぞれ等しいので$\triangle AOP \sim \triangle NKC$となる。それから、$AO \parallel NK$は$\triangle AOB \sim \triangle NKB$であることも表している。これら2つの相似から$AB:NB$$=AO:NK$$=AP:NC$が判り、$\angle BAP=\angle BNC$($\because$平行線の錯角)と併せて、2辺の比とその間の角がそれぞれ等しいので$\triangle ABP \sim \triangle NBC$が成立する。ゆえに$\angle ABP=\angle NBC$であり、対頂角が等しいので3点$P,B,C$はこの順で同一直線上に存在する。
$\triangle AJP$と$\triangle AJI$について、$\angle PAJ=\angle PAC-\angle JAC$$=180^{\circ}-\angle ACL-\angle JAK$$=180^{\circ}-2\angle AIJ$$=\angle IAJ,$ $\angle AJP=\angle AJO$$=\angle AJK$$=\angle AJI,$ $AJ=AJ$より、1辺とその両端の角がそれぞれ等しいので$\triangle AJP \equiv \triangle AJI$が成り立つ。よって$AI=AJ=AP$である。
$B$から引いた$CL$の平行線と$AG,$ $\triangle ABJ$の外接円(この円を$\omega$とする)の交点をそれぞれ$Q,R$とすると、円周角の定理より$\angle ARB=\angle AJB=8^{\circ},$ $\angle JRB=\angle JAB=8^{\circ}$である。ところで、$\angle JBG=\angle DCF$から$BJ \parallel DC$であることを利用すると、$\angle JBR=\angle DCL$$=\angle DCA+\angle ACL$$=\angle DCA+\angle AIJ=90^{\circ}$が導かれ、円周角の定理の逆により線分$JR$が$\omega$の直径であるといえる。すなわち$\angle JAR=90^{\circ}$となり、$\angle JAE=\angle BAE-\angle BAJ=90^{\circ}$と併せて、3点$A,E,R$はこの順で同一直線上に存在する。さらに$\angle AJR=90^{\circ}-\angle ARJ=74^{\circ}$であり、$\angle AJG=74^{\circ}$と併せて、3点$J,G,R$もこの順で同一直線上に存在する。
$B$から引いた$CL$の平行線と$AG,$ $\triangle ABJ$の外接円(この円を$\omega$とする)の交点をそれぞれ$Q,R$とすると、円周角の定理より$\angle ARB=\angle AJB=8^{\circ},$ $\angle JRB=\angle JAB=8^{\circ}$である。ところで、$\angle JBG=\angle DCF$から$BJ \parallel DC$であることを利用すると、$\angle JBR=\angle DCL$$=\angle DCA+\angle ACL$$=\angle DCA+\angle AIJ=90^{\circ}$が導かれ、円周角の定理の逆により線分$JR$が$\omega$の直径であるといえる。すなわち$\angle JAR=90^{\circ}$となり、$\angle JAE=\angle BAE-\angle BAJ=90^{\circ}$と併せて、3点$A,E,R$はこの順で同一直線上に存在する。さらに$\angle AJR=90^{\circ}-\angle ARJ=74^{\circ}$であり、$\angle AJG=74^{\circ}$と併せて、3点$J,G,R$もこの順で同一直線上に存在する。
$Q$から引いた$AJ$の平行線と$JR$の交点を$S$とする。このとき$AP \parallel QB$より$\triangle GAP \sim \triangle GQB$、よって$AP:QB$$=GA:GQ$であり、かつ$AJ \parallel QS$より$\triangle GAJ \sim \triangle GQS$、よって$AJ:QS$$=GA:GQ$である。したがって$AP:QB$$=AJ:QS$となり、$AJ=AP$から$QB=QS$、つまり$\triangle QBS$が二等辺三角形であると判る(点$G$を中心に$\triangle AJP$を縮小するイメージで示してもよい)。いま、$AJ \parallel QS$より$\angle ABR=\angle AJR=\angle QSR$なので、$\angle QBS=\angle QSB$に注意すると$\angle MBS=\angle MSB$となる。つまり$QB=QS,$ $MB=MS$から、$MQ$は線分$BS$の垂直二等分線であり、ゆえに$\angle BMQ=\angle SMQ$である。
以上の議論より、点$Q$は$\angle ARM$の二等分線上および$\angle AMR$の二等分線上にあると示せたので、点$Q$は$\triangle AMR$の内心であることが明らかとなる。ここから$\angle MAQ$$=\angle RAQ$$=\dfrac{\angle BAE}{2}=49^{\circ}$を得るので、$\angle AGR$$=180^{\circ}-\angle GAR-\angle ARG=115^{\circ}$が従う。$DF \parallel JR$より求める角度は$\angle AGR$に等しく、結局本問の答えは$115^{\circ}$であると証明された。
以上の議論より、点$Q$は$\angle ARM$の二等分線上および$\angle AMR$の二等分線上にあると示せたので、点$Q$は$\triangle AMR$の内心であることが明らかとなる。ここから$\angle MAQ$$=\angle RAQ$$=\dfrac{\angle BAE}{2}=49^{\circ}$を得るので、$\angle AGR$$=180^{\circ}-\angle GAR-\angle ARG=115^{\circ}$が従う。$DF \parallel JR$より求める角度は$\angle AGR$に等しく、結局本問の答えは$115^{\circ}$であると証明された。
あまりにも短い別解(立見鶏( Twitter )氏から紹介されました)
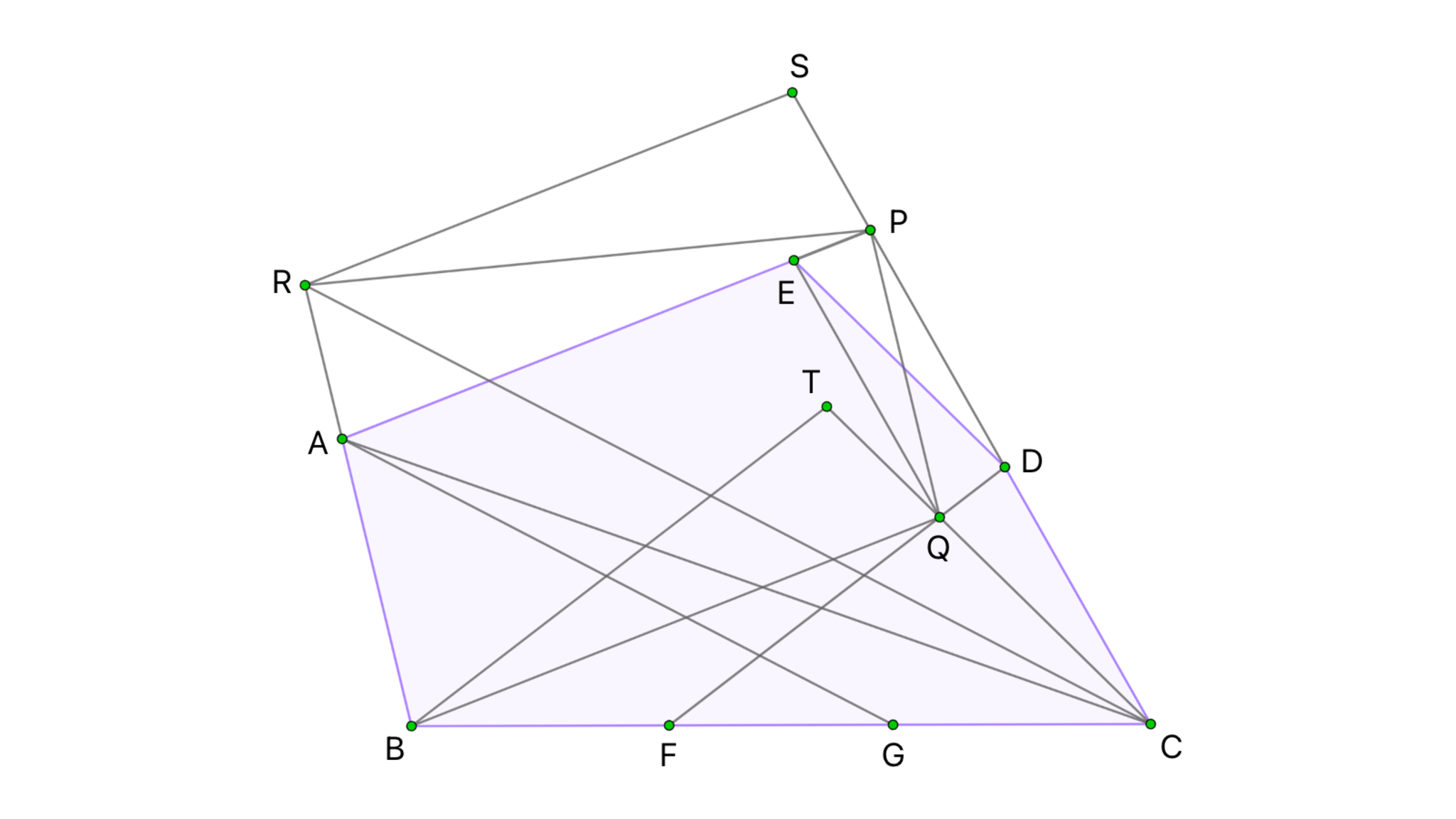T-GUESS主催者胃痛案件
$AE$と$CD$の交点を$P$とし、$\triangle CEP$の外心を$Q$とする。円周角の定理から$\angle CQE=360^{\circ}-2\angle CPE=164^{\circ}$が成り立ち、$QC=QE$に注意すると四角形$CDEQ$はひし形であると判る。したがって$\angle EPQ=82^{\circ}$となり、$\angle BAP=98^{\circ},$$AB=PQ$と併せて、四角形$ABQP$は平行四辺形であることが明らかとなる。
ここで半直線$BA$上に$AP=PR$となる点$R$をとり、$R$から引いた$AB$の平行線と半直線$CD$との交点を$S$とする。このとき$\angle APC=180^{\circ}-\angle CAP-\angle ACP=98^{\circ},$$\angle BAP=98^{\circ}$より、四角形$APSR$は等脚台形となっている。いま、$\triangle PRS \equiv \triangle QBT$となるように点$T$をとると、$\angle BQC$$=360^{\circ}-\angle BQP-\angle CQP$$=360^{\circ}-\angle BAP-\angle CQP=114^{\circ},$$\angle BQT=\angle RPS=66^{\circ}$より$\angle BQC+\angle BQT=180^{\circ}$が判り、3点$C,Q,T$はこの順で同一直線上に存在するといえる。
ここで半直線$BA$上に$AP=PR$となる点$R$をとり、$R$から引いた$AB$の平行線と半直線$CD$との交点を$S$とする。このとき$\angle APC=180^{\circ}-\angle CAP-\angle ACP=98^{\circ},$$\angle BAP=98^{\circ}$より、四角形$APSR$は等脚台形となっている。いま、$\triangle PRS \equiv \triangle QBT$となるように点$T$をとると、$\angle BQC$$=360^{\circ}-\angle BQP-\angle CQP$$=360^{\circ}-\angle BAP-\angle CQP=114^{\circ},$$\angle BQT=\angle RPS=66^{\circ}$より$\angle BQC+\angle BQT=180^{\circ}$が判り、3点$C,Q,T$はこの順で同一直線上に存在するといえる。
$Q$は線分$DF$上にあるので$\angle CQF=98^{\circ}$であり、$\angle CTB=\angle PSR=98^{\circ}$と併せて$BT \parallel FQ$を得る。長さの比を移していくと、
$$BG:GC=CF:FB=CQ:QT=QP:PS=BA:AR$$
より、$AG \parallel RC$が導かれる。$PC=PA=PR$より$\angle PCR=\dfrac{180^{\circ}-\angle CPR}{2}=33^{\circ}$が従うので、求める角度は$\angle CDF+\angle PCR=$$115^{\circ}$と示された。
主催者コメント
幾何力の 足らぬ頭で 主催とは ＿＿＿＿詠み人：匿
本問の正解者は4名(うち非エスパー2名)であった。盛大な拍手を送りたい。
投稿日：2022年5月9日
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中