反転を拡張してみる
肝心の拡張は自分で考えた内容なので参考文献は無いです。変な部分があれば教えてください。
反転を拡張する前に通常の反転を確認しておきましょう。
反転
中心$O$半径$r$の基準円$\Gamma $,点$P$が与えられている時、$P$の$\Gamma $に関する反転とは、$P$を$O$から$P$に引いた半直線上にあり$OP \cdot OP'= r^2 $を満たす点$P'$に写す写像のことを言う。
ただし$P$が無限遠点ならば反転によって$\Gamma $の中心に写るとする。
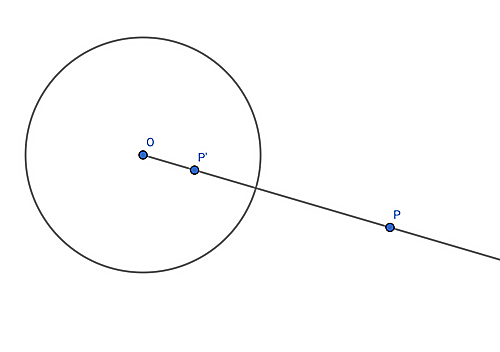 反転
反転
反転によって接する、接さないという位置関係は変わらず、基準円と直交する円は反転によって変化しません。更に基準円の中心を通る円は基準円の中心を通らない直線に写されます。(参考文献より)
ところで$r^2$から方冪を連想するので
反転を拡張する
中心$O$半径$r$の円$\Gamma $,点$P,P',Q$が与えられていて$Q$の$\Gamma $における方冪の値を$\rho= \vert OQ^2-r^2 \vert $とする。P'がQからPに引いた半直線上にあり$|PQ| \cdot|QP'|=\rho $を満たす時、$PをP'$に写す写像を$P$の$\Gamma $に関する$Q$における反転
ただし$P$が無限遠点ならば拡張した反転によって$Q$に写るとする。
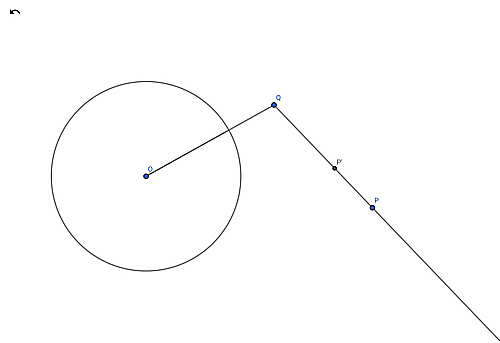 反転2
反転2
拡張した反転の性質
の内私がこれこそが通常の反転と一線を画すものだと思うものを一つ紹介します。
円$\Gamma $とその接線$\ell $があり$Q$を$\ell $上にない点とする。$\ell $の$\Gamma $に関する$Q$における反転は$\ell $を$\Gamma $に接し$Q $を通る円$ \varOmega $に写す。
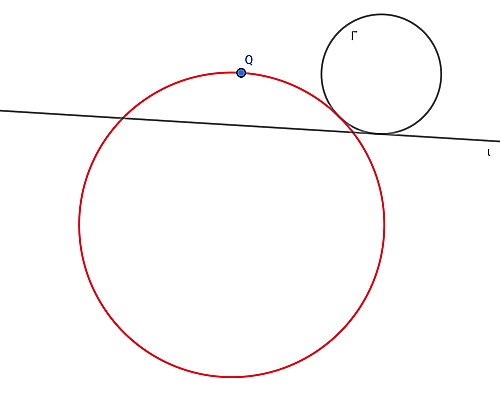 定理
定理
$\ell $と$\Gamma $の接点を$A$とし$AQ$と$\Gamma $の$A$以外の交点を$B$とする。$B$が反転による$A$の像であることは拡張された反転の定義からすぐにわかる。$B$から$\Gamma$に引いた接線と$\ell$との交点を$Z$とする。$\ell $上の点$C$を取り$QC$と$\varOmega $との$Q$以外の交点を$D$とおく。このとき$|QA| \cdot|QB|=|QD| \cdot|QC|$なので方冪の定理の逆から$ABCD$は同一円周上。以上から$\angle ZAB=\angle ZBA=\angle BDQ $が言え接弦定理の逆より$\varOmega$は$\Gamma$に$B$で接する$。示された。 $
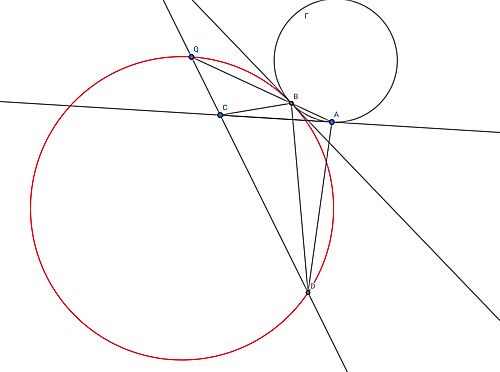 証明
証明
接線の写像ではなく、接する円の写像でも似たような事が言えます。
この定理また拡張した反転の使いどころは多いとは言えないですが痒いところに手が届く絶妙な威力があります。是非その痒いところを探してみてください。
ありがとうございました。
