文献あり

自然言語における継続とCPS文法

はじめに

「継続 (continuation)」なる論理学・計算機科学上の概念があります。Wikipediaで調べると

計算機科学における継続（けいぞく、continuation）とは、プログラムの実行においてある時点において評価されていない残りのプログラム（the rest of the program）を意味するものであり、手続き（procedure）として表現されるものである。
【Wikipedia「継続」の項目。アクセス日時:15May2022】

とあります。上記以外の分野で継続を使うことはないのか調べると、自然言語（=日常の言葉）でも使われていることを知りました。この文脈だと、継続がまあまあわかりやすいので、自分の勉強を兼ねて本記事で書いておこうと思います。具体的には

自然言語における継続を、量化子"everyone"を通して概観する
CPS文法の解説

の2つを取り扱います。

以下注意です：

主にRef.[1]に基づいて説明します。参考としてRef.[2][3]もあげておきます。また、ここに述べた形式化以外にも形式化が存在することを断っておきます。
日本語訳は、専門的に使われているものと違う場合があると思います。ご容赦ください。
某noteに、この記事の前半と似たようなのがありますが、同一筆者です。

自然言語の形式化と継続

まず、自然言語（ここでは英語）を形式化します。そのうえで、継続はどんなものか、どのように現れ役に立つのかを見ます。

記号の定義

以下で用いられる記号を定義しておきます。

要素の略称	意味	型	例
S	文 (Sentences)	t (真理値)	I have a pen.; She loves you.;...
NP	名詞句 (Noun Phrase)	e (entity, 実体)	John; a cat; dogs; a cup of tea ; ...
VP	動詞句 (Verb Phrase)	e$\rightarrow$ t	swim ; have a pen ; loves you; ...
Vi	自動詞 (Verb, intransitive))	e$\rightarrow$ t	agree; swim; leave;...
Vt	他動詞 (Verb, transitive)	e$\rightarrow$(e$\rightarrow$ t)	love; have; see; ...

Sは文を表します。NPは名詞句です。「句」なので一単語とは限らず、a cup of teaのようなものも含まれます。VPは「動詞句」です（勝手に日本語に訳したので、もっと適切な訳があるかもしれません）。要するに「目的語まで含めた動詞のかたまり」です。自動詞はそれだけでVPです。他動詞の場合は"have a pen"や"loves you"のように目的語も含めVPです。ViとVtはそれぞれ自動詞・他動詞です。

ちなみに、冠詞はdeterminer（限定子）と呼ばれるものの1つですが、以下では特段取り扱いません。

それぞれの要素には型が定義されています。文は命題なので、真理値の型t(true or false)をとります。名詞句はなんらかの現実の実体と対応するので、型e(entity)をとります。動詞句は「主語を与えると文を返す関数」と考え、型e$\rightarrow$tを取ります。自動詞はVPと同じ型です。他動詞は、「目的語を与えると『主語を与えると文を返す関数』を返す関数」と考え、e$\rightarrow$(e$\rightarrow$ t)の型をとるとします。Vtを「主語と目的語の2変数を与えると文を返す2変数関数」とみなすこともできますが、ここではカリー化された高階関数とします。

以下、本記事で登場する単語に対応する記号を定義します：

単語	要素	型	記号
John	NP	e	${\bf j}$
Mary	NP	e	${\bf m}$
left	VP	e$\rightarrow$ t	${\bf left}$
saw	Vt	e$\rightarrow$(e$\rightarrow$ t)	${\bf saw}$

一番右のカラムの太字は文の単語ではなく、形式化された文法における記号です。VPやVtの記号は「演算子」です。

これらの定義のもと、「直接的な文法(direct grammar、以下DGと略す)」での文の形式化は以下のようになります：

文	DGにおける形式化
John left.	$\bf \text{left j}$
John saw Mary.	$\bf \text{saw m j}$

以下記号の型を"${\bf j}$:e"のように表すことにします。

"$\bf \text{left j}$"は、$\bf \text{j}$: eを$\bf \text{left}$: e$\rightarrow$tに適用（=関数の引数として$\bf \text{j}$を与える）し、文S(型t)を得ることを表します。
"$\bf \text{saw m j}$"は、まず目的語$\bf \text{m}$: eを$\bf \text{saw}$: e$\rightarrow$(e$\rightarrow$t)に適用し、e$\rightarrow$t型の関数（つまりはVP）を得て、さらに主語$\bf \text{j}$: eをこれに適用して文Sを得ることを表します。

図にすると以下のようになります：

"John left."と"John saw Mary."の形式化の図示

継続の必要性: "everyone"の形式化

"Everyone left."という文章を考えます。ここでeveryoneの型は何かと考えます。eと考えるのはいささか不自然です。「everyone=皆」というのは特定の実体を表すのではなく、量化を表しています。everyoneの対立概念"no one"を考えると、これがeではないことははっきりするかと思います。

解決策1 $\bf\text{everyone}$: (e$\rightarrow$ t)$\rightarrow$t

そこで、"everyone"が示す意味に対応する記号$\bf \text{everyone}$の型を
(e$\rightarrow$ t)$\rightarrow$t
だとしてみます（Ref.[3]）。
すると"Everyone left."の形式化
$\bf \text{everyone left}$
は、$\bf \text{everyone}$: (e$\rightarrow$ t)$\rightarrow$t に $\bf \text{left}$: e$\rightarrow$ tを適用して型tを返すことを表し、整合的です。

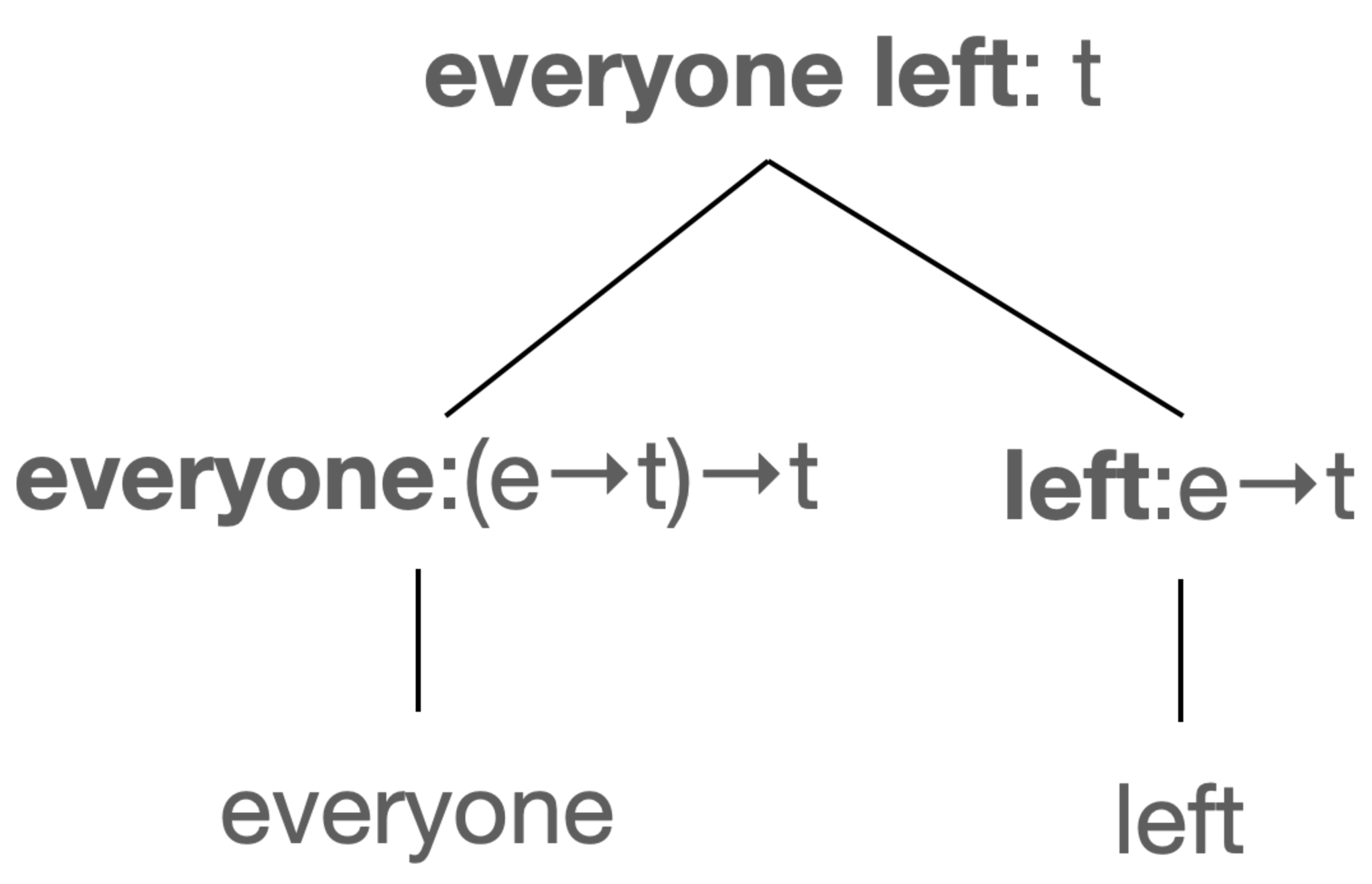解決策1における"Everyone left."の形式化の図示

しかしながら、"John saw everyone."のように、everyoneが目的語として使われると、型に整合性がなくなります。 なぜなら"saw everyone"はVP（型e$\rightarrow$t）となるべきですが、$\bf\text{saw}$:e$\rightarrow$(e$\rightarrow$t)と$\bf\text{everyone}$: (e$\rightarrow$t)$\rightarrow$eを組み合わせて型e$\rightarrow$tは作れないからです。

解決策1における"John saw everyone."の形式化の図示。型が不整合。

解決策2 継続を用いる

継続を用いてこの問題を解決します。

ここでラムダ計算を導入します。この計算では$\lambda$という記号をつかって引数を表します。$\lambda x.P x$と書いたら、「$x$を引数として、$x$を$P$に適用する関数」という意味です。$f(x)=P x$みたいなものです。

さて、everyoneを
$$ \lambda P. \forall x. P x $$
とします。これは、$P$を引数とし、量化された$x$を$P$に適用する関数です。

ここで"John saw everyone."(★)において、$P$に代入するものを、「sawの目的語を変数にした(★)の文の関数」とします。ラムダ計算の言葉で書くと
$$ \lambda x.{\bf \text{saw }} x \ {\bf \text{j}} $$
です。すると(★)は
$$ (\lambda P. \forall x. P x)(\lambda y.{\bf \text{saw }} y \ {\bf \text{j}}) $$

と形式化されます。これを変形すれば
\begin{align} (\lambda P. \forall x. P x)(\lambda y.{\bf \text{saw }} y \ {\bf \text{j}})\leadsto \forall x. {\bf \text{saw }} x \ {\bf \text{j}} \end{align}
となり（$P$に$\lambda y.{\bf \text{saw }} y \ {\bf \text{j}}$を代入し、この引数$y$を$\forall$で束縛する。$A\leadsto B$はAからBが導かれるの意）、"John saw everyone."の意味とも整合的です。

この「sawの目的語を変数にした(★)の文の関数」$\lambda x.{\bf \text{saw }} x \ {\bf \text{j}}$が、この場合の継続です。

振り返って、"Everyone left."を継続により形式化します。この場合の継続は、文の主語を変数とした文関数"$\lambda x.{\bf \text{left }}x$です。形式化された文
$$ \bf \text{everyone left} $$
をラムダ計算で書けば
\begin{align} (\lambda P. \forall x. P x)(\lambda y.{\bf \text{left }} y) \leadsto \forall x. {\bf \text{left }} x \end{align}
であり、これも整合的です。

ひとつ注意です。継続を定める場合、何を変数とするかとともに、スコープをきることも重要です。上記の文の例では、文の中に文が埋め込まれるような下部構造がないので問題ないですが、"You said that Mary went to school."のように節が存在するような場合、大きな構造 "You said (NP)."における継続か、下部構造"Mary went to school."における継続かを見定める必要があります。

中間まとめ：継続とは

ここで扱った自然言語における継続とは

「文章に存在する何らかの要素を変数とした"文章の関数"」

と言えます。
"John saw Mary."の文章を例にとると

主語を変数とした継続は $\lambda x.{\bf \text{saw m }}x$
目的語を変数とした継続は $\lambda y.{\bf \text{saw }}y {\bf\text{ j}}$
他動詞を変数とした継続は $\lambda R.R {\bf \text{ m j}}$

そして、"everyone"は「継続を受け取り、受け取った関数の引数を$\forall$で束縛された変数にして、S（文）を返す関数」になります。

上で見たように、量化子を含む文章は、継続を用いて形式化すると、構文解析的に自然です。

CPS文法

CPSとは"Continuation-Passing Style"=「継続渡しスタイル」の略です。CPS文法とはこのスタイルを使って文を綴る際の文法です。CPS文法で文を記述しても、元の文（DGによる文）と意味的には同じになります。以下これに関して説明します。

CPS文法とは何か

CPSとは何かを大雑把に説明すると「『継続を引数とし、文を返す関数』で綴るスタイル」です。まさに"Continuation-Passing Style（継続渡しスタイル）"です。

以下にDGにおける要素の型、継続の型、そしてCPS文法での型を表にしておきます。

要素	DGにおける型	継続の型	CPS文法での型
S	t	t$\rightarrow$t	(t$\rightarrow$t)$\rightarrow$t
NP	e	e$\rightarrow$t	(e$\rightarrow$t)$\rightarrow$t
VP	e$\rightarrow$ t	(e$\rightarrow$ t)$\rightarrow$ t	((e$\rightarrow$ t)$\rightarrow$ t)$\rightarrow$t
Vt	e$\rightarrow$(e$\rightarrow$ t)	(e$\rightarrow$(e$\rightarrow$ t))$\rightarrow$ t	((e$\rightarrow$(e$\rightarrow$ t))$\rightarrow$ t)$\rightarrow$t

上の表の3つの型の関係は明らかです。右のセルの型は、左のセルの型を入力として型tを返す関数になっています。よって一番右の列の型は、「継続を引数とし、文を返す関数」です。

CPS文法のルール

さて、CPS文法に関するルールを設定します。

以下、ある要素・単語の記号を$\text{N}$としたとき、$\text{N}$に対応するCPS文法での記号を$\overline{\text{N}}$で表すことにします。$\text{N}$から$\overline{\text{N}}$への変換をCPS変換と呼びます。

上で見たように、継続とは、「何らかの文の要素を変数とした『文章の関数』」です。そして、CPS文法での記号とは、「継続を引数とし、回答型(answer type、何らかの規定的な型)を返す関数」と言えます。
ここまで例示した文章の場合、回答型はt型です。つまりは「継続をうけてtを返す」のが継続化された文の要素です。

CPS変換およびCPS変換された記号の合成に関するルールは以下です：

定数$\alpha$のCPS変換およびCGにおける単語の合成ルール

$\overline{\alpha} := \lambda\kappa.\kappa\alpha$ $\ \ \ $ 定数$\alpha$のCPS変換の定義
$\overline{\text{MN}} := \lambda\kappa.\overline{\text{M}}(\lambda m.\overline{\text{N}}(\lambda n.\kappa(mn)))$ $\ \ \ $ CPS変換された記号$\overline{\text{M}}$と$\overline{\text{N}}$の合成ルール

1.2.における型に関してコメントしておきます。

1.に関して:
${\alpha}$の型がAのとき、$\kappa$が受けるオブジェクトの型はA$\rightarrow$tであり、よって$\overline{\alpha}$の型は(A$\rightarrow$t)$\rightarrow$ tです。
2.に関して:
記号$\text{N}$の型がAのとき、$\overline{\text{N}}$の型は(A$\rightarrow$t)$\rightarrow$tです。$\overline{\text{M}}$の型がA$\rightarrow$Bのとき、$\overline{\text{M}}$の型は((A$\rightarrow$B)$\rightarrow$t)$\rightarrow$tです。

上記の定義1の2.が整合的なら、$\text{MN}$の直接的な型はBなので、そのCPS変換$\overline{\text{MN}}$の型は(B$\rightarrow$t)$\rightarrow$tになるはずです。これを確かめておきます：

いま、$\overline{\text{M}}$を$\lambda \kappa.\kappa \text{M}$,$\overline{\text{N}}$を$\lambda \kappa.\kappa \text{N}$とします。これを上式に代入すると
\begin{align} \overline{\text{MN}} = \lambda\kappa.(\lambda\kappa'.\kappa'\text{M})(\lambda m.(\lambda\kappa''.\kappa''\text{N})(\lambda n.\kappa(mn))) \end{align}
これを変形していくと
\begin{align} &\lambda\kappa.(\lambda\kappa'.\kappa'\text{M})(\lambda m.(\lambda\kappa''.\kappa''\text{N})(\lambda n.\kappa(mn)))\\ \rightarrow&\lambda\kappa.(\lambda\kappa'.\kappa'\text{M})(\lambda m.\kappa(m\text{N}))\\ \rightarrow&\lambda\kappa.\kappa(\text{MN}) \end{align}
となります。これは確かに$\overline{\text{MN}}$のCPS変換であり、ゆえに型は(B$\rightarrow$t)$\rightarrow$tです ($\kappa$は型B$\rightarrow$tの変数)。${}_\blacksquare$

ちなみに、以下の定理

Curry-Howard同型対応

論理の証明体系（自然演繹）と型付の計算体型（≃関数型プログラミング）における諸概念が対応している(Ref.[4])。命題は型、証明はその型の関数と対応。

を思い出すと、上記コメント「2.に関して」における型の推移は、論理学において
　(A$\rightarrow$ C)$\rightarrow$C, ((A$\rightarrow$B)$\rightarrow$C)$\rightarrow$C から (B$\rightarrow$C)$\rightarrow$Cが導ける　（★★）
ことを意味します。

この記事の範囲内ではこれで十分なのですが、本来$\overline{\text{M}}, \overline{\text{N}}$の型はもっと一般的であり

$\lambda\kappa.\overline{\text{M}}(\lambda m.\overline{\text{N}}(\lambda n.\kappa(mn)))$:(B$\rightarrow$E)$\rightarrow$D ::= $\overline{\text{M}}$:((A$\rightarrow$B)$\rightarrow$C)$\rightarrow$D $\ \ $ $\overline{\text{N}}$:(A$\rightarrow$E)$\rightarrow$C

になります(Ref.[1] Eq.(10))。右辺は$\overline{\text{M}}$と$\overline{\text{N}}$の合成の意味です。
これは
　((A$\rightarrow$B)$\rightarrow$C)$\rightarrow$D, (A$\rightarrow$E)$\rightarrow$C $\vdash$ (B$\rightarrow$E)$\rightarrow$D
が証明できることを示しています。Ref.[1]ではFig.1において、論理学における上式の証明を行っています。この式でC=D=Eとしたのが(★★)です。

CPS文法の具体例

具体的にCPS文法における記述を見ていきます。上記の定義1を使って文を形式化します。

John left.

CPS文法における"John left."は以下です：

文の構造　[S [NP John] [VP left]]
CPS文法　$\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{left}}](\lambda f.[\lambda\kappa''.\kappa''{\bf \text{j}}](\lambda x.\kappa(fx)))$

これを変形していくと
\begin{align} &\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{left}}](\lambda f.[\lambda\kappa''.\kappa''{\bf \text{j}}](\lambda x.\kappa(fx)))\\ &\rightarrow \lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{left}}](\lambda f.\kappa(f {\bf \text{j}}))\\ &\rightarrow \lambda\kappa.\kappa ({\bf \text{left j}}) \end{align}
を得ます。$\lambda\kappa.\kappa ({\bf \text{left j}})$は確かに${\bf \text{left j}}$のCPS変換であり、上記のルールが整合的であることがわかります。

$\lambda\kappa.\kappa ({\bf \text{left j}})$に恒等的な継続$\lambda \kappa.\kappa$を適用すれば、DGにおける文${\bf \text{left j}}$を得ます。

"Everyone left.", "John saw everyone."

"Everyone left."は以下のようになります：

文の構造　[S [NP Everyone] [VP left]]
CPS文法　$\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{left}}](\lambda f.[\lambda\kappa''.\forall x.\kappa'' x](\lambda y.\kappa(fy)))$

これも変形すれば
\begin{align} &\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{left}}](\lambda f.[\lambda\kappa''.\forall x.\kappa'' x](\lambda y.\kappa(fy)))\\ \rightarrow&\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{left}}](\lambda f.\forall x. \kappa(f x))\\ \rightarrow & \lambda\kappa.(\forall x.\kappa ({\bf \text{left }}x)) \end{align}
を得ます。恒等的な継続を適用するとDGの文$\forall x.{\bf \text{left }} x$に戻ります。

"John saw everyone."は以下のようになります：

文の構造　[S [NP John] [VP [Vt saw] [NP everyone]]]
CPS文法　$\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{saw}}](\lambda f.[\lambda\kappa''.\forall x.\kappa'' x](\lambda y.(\lambda\kappa^{(3)}.\kappa^{(3)}({\bf \text{j}}))(\lambda x.\kappa(\kappa' xy)))$

変形すると
\begin{align} &\lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{saw}}](\lambda f.[\lambda\kappa''.\forall x.\kappa'' x](\lambda y.(\lambda\kappa^{(3)}.\kappa^{(3)}({\bf \text{j}}))(\lambda x.\kappa(f xy)))\\ &\rightarrow \lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{saw}}](\lambda f.[\lambda\kappa''.\forall x.\kappa'' x](\lambda y.\kappa(f {\bf \text{ j }} y)))\\ &\rightarrow \lambda\kappa.[\lambda \kappa'.\kappa'{\bf \text{saw}}] (\lambda f.\forall y.\kappa(f{\bf \text{ j }} y))\\ &\rightarrow \lambda\kappa.\forall y.\kappa({\bf \text{saw j }} y)) \end{align}
を得ます。恒等的な継続を適用するとDGの文$\forall x.{\bf \text{saw j }} x$に戻ります。

量化子に関する不定性

定義1の2.に対し、"逆の"評価規則があります：

CPS文法における単語の合成ルール2：右から左への評価規則

$\overline{\text{MN}} := \lambda\kappa.\overline{\text{N}}(\lambda m.\overline{\text{M}}(\lambda n.\kappa(mn)))$

これは定義1の2.とは逆で、$\overline{\text{N}}$を評価してから$\overline{\text{M}}$を評価する規則です。

この2つのルールは、量化子が1つしかないときには何の差もないですが、2つ以上ある場合、差が生じます。例えば次の文章を考えます。

Someone saw everyone.
a. $\exists x \forall y.{\bf \text{saw }}x \ y$
b. $\forall y \exists x.{\bf \text{saw }}x \ y$

上の文章をa.の意味で解釈すると「ある特定の誰かさんがみんなを見ている」という意味になり、b.の意味で解釈すると「誰もを誰かが見ている（みんな誰かに見られている、お互いを見ている）」という意味になります。これは定義1の2.と定義2の2.で違いが生じる例です。この2つの解釈はどちらも可能なので、どちらの定義を適用するかは（文脈を考慮しなければ）不定性として残ります。

まとめ

本記事では、自然言語における継続に関して、Ref.[1]に基づき説明しました。量化子"everyone"を形式化された文に導入するためには継続を用いるのが良いこと、さらにCPS文法に関して言及しました。

Ref.[1]では、継続が重要な役割をする例として、Focus（どの単語を強調するか）、Coordination（and, orによる並列・等置の解釈）、Misplaced Modifiersに関しても議論しています。最後のMisplaced Modifiersとは次の文

a. An occasional sailor walked by.
b. John drank a quiet cup of tea.

におけるoccasionalやquietのことです。「occasional=たまの、時折」はsailorにかかっているように見えますが、「たまの海兵」では意味がわかりません。これは意味的には"An sailor occasionally walked by."ということです。b.も「静かな一杯の紅茶」ではなく、「Johnは静かに紅茶を飲んだ」ということです。つまり、これらの形容詞はローカルに一単語に作用しているのではなく、文全体に副詞的に作用しています。

これらを総合して考えると、継続は、単語がローカルではなくある程度のグローバルな作用を持つときに有用な概念と言えるかと思います。

おしまい。