犬でもわかる Diffie-Hellman 鍵共有
概要
Diffie-Hellman 鍵共有とは、二人の間で同じ秘密の値を作成する 公開鍵暗号方式です。二人の間で同じ秘密の値を共有できれば、あとはそれを共通鍵として共通鍵暗号方式でやり取りができます。
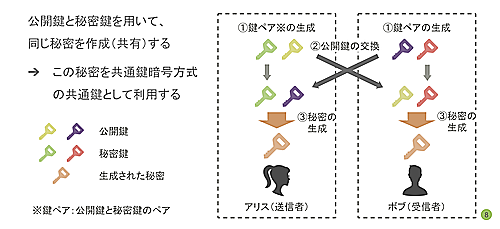Diffie-Hellman鍵共有の概要
前提知識
公開鍵暗号方式が前提知識となります。公開鍵暗号方式についてよくわかっていない方は、この スライド を見て下さい。
数学的準備
まずはDiffie-Hellman鍵共有を学ぶ上で必要な、数学に関する知識を見ていきましょう。（高校数学の範囲内ですので、理解している人は飛ばしましょう。）
剰余演算
割り算の余りを求める演算について、次のように定義します。
$a \bmod b$ は$a$を$b$で割ったときの余りである。
具体的な余りを求める例を見ていきましょう。
$10$を$6$で割ったあまりは、$4$である。
$$10 \bmod 6 = 4$$
$20$を$7$で割ったあまりは、$4$である。
$$20 \bmod 7 = 6$$
$3\times4$を$7$で割ったあまりは、$5$である。
$$3\times4 \bmod 7 = 12 \bmod 7 = 5$$
$2^3$を$7$で割ったあまりは、$1$である。
$$2^3 \bmod 7 = 2 \times 2 \times 2 \bmod7 = 8 \bmod 7 = 1$$
累乗の累乗
累乗の累乗について次のような定理が成り立ちます。
任意の自然数 $g$，$a$，$b$，$n$ と $A =g ^ a \bmod n$ に対して、次の式が成り立つ。
$$A^b \bmod n = g ^ {ab} \bmod n$$
累乗の累乗をする例を見ていきましょう。
$A = 2^3 \bmod 10$ならば
$$A^2 \bmod 10 = 2 ^ {3 \times 2} \bmod 10 = 2 ^ 6 \bmod 10 = 64 \bmod 10 = 4$$
仮定
公開鍵暗号方式の多くは、特定の計算が困難なことを仮定としておくことで、実現されています。
Diffie-Hellman鍵共有は、DH問題が解けないことを仮定とする、DH仮定を元に成り立っています。
離散対数問題
DH問題について話す前に、現在多くの暗号で用いられる離散対数問題（DLP）について説明します。
離散対数問題（DLP）
大きな素数$n$ と1 以上$n$未満の自然数 $g, x$ を もちいて、$y$ を次のようにおく。
$$y = g ^ x \bmod n$$
計算上次のような事実が存在する。
- $(g, x, n)$ から $y$ は短い時間で計算できる
- $(g, y, n)$ から $x$ は計算にかなり時間がかかる
特にこの 2. の事実を離散対数問題という。
特にこの 2. の "かなり時間がかかる"というは、$x, n, g$の値によっては、現実的に計算不可能なことを表します。
DH 問題
DH問題は離散対数問題の上で成り立つ計算上困難な問題です。
Diffie-Hellman 鍵共有は、DH問題を用いています。
DH問題
大きな素数$n$ と1 以上$n$未満の自然数 $g, x, y$ 、$K_A$, $K_B$ を次のようにおく。
$$ \begin{align} K_A = g ^ x \bmod n \\ K_B = g ^ y \bmod n \\ K_{AB} = g ^ {xy} \bmod n \end{align} $$
計算上次のような事実が存在する。
- $(n, x, K_B)$ から $K_{AB}$ は短い時間で計算できる
- $(n, y, K_A)$ から $K_{AB}$ は短い時間で計算できる
- $(g, n, K_A, K_B)$ から $K_{AB}$ は計算にかなり時間がかかる。
特にこの 3. の事実をDH問題という。
特にこの 2. の "かなり時間がかかる"というは、$x, y, n, g$の値によっては、現実的に計算不可能なほど時間がかかることを表します。
- ~ 2. が離散対数問題を解かずに、高速に計算できることを、以下に証明します。
$$ (K_B) ^ x \bmod n = (g ^ y) ^ x \bmod n = g ^ {xy} \bmod n = K_{AB}$$
$$ (K_A) ^ y \bmod n = (g ^ x) ^ y \bmod n = g ^ {xy} \bmod n = K_{AB}$$
手順
以下に手順をまとめました。アリスとボブが同じ秘密を共有するために、Diffie-Hellman鍵共有をします。
準備
大きな素数$n$ と1 以上$n$未満の自然数 $g$ を選び事前に共有します。（これらは漏洩しても問題ないです。）
鍵ペア生成
アリスは 乱数$x$を計算し、 $K_A = g ^ x \bmod n$ を求めます。
ボブも乱数 $y$ を計算し、$K_B = g ^ y \bmod n$ を求めます。
$x$と$y$を秘密鍵、$K_A$と$K_B$を公開鍵とします。（公開鍵は漏洩しても問題ないです。秘密鍵は漏洩するとまずいです。）
公開鍵の交換
アリスは $K_A$ をボブに、ボブは $K_B$をアリスに送信します。（これらは漏洩しても問題ないです。）
共有する秘密の計算
アリスは自身の秘密鍵$x$と$K_B$を用いて、秘密$K_{AB}$次のように計算します。
$$(K_B)^x \bmod n = (g ^ y)^x \bmod n = g ^ {xy}\bmod n = K_{AB}$$
ボブは自身の秘密鍵$y$と$K_A$を用いて、秘密$K_{AB}$次のように計算します。
$$(K_A)^y \bmod n = (g ^ x)^y \bmod n = g ^ {xy}\bmod n = K_{AB}$$
安全性
$(g, n, K_A, K_B)$ は漏洩される可能性がありますが、DH問題により $K_{AB}$ 計算するには、離散対数問題を解く必要があり、現実的な時間では計算することができません。
まとめ
Diffie-Hellman 鍵共有について、まとめました。