傍心と外心に関する有名問題の初等的解法
準備
- 必要な知識
相似、三角形の五心、円周角の定理 - 紙、シャーペン、定規、コンパスがあったほうがいい
図は添付していますが、分かりにくい時のために図を描きながら見ることをオススメします。添付した図の三角形に似せて描くと楽です。 - 注意
大雑把な説明でとどめています。ある程度の理解を必要とするかもしれません
また、添付した図の文字が見にくい上に、基本点の名前は図参照なので、分かりにくい所は書くよう随時編集するかたちでいきます。 - 有向角の知識が曖昧です。正しくなかったらご指摘ください。。
説明を省く事実
ここはてきとうに済ませましょう
三角形$ABC$において$∠A$の内角、外角の二等分線と$BC$の交点をそれぞれ$D,E$として、$BD:DC=BE:CE$が成り立つ。
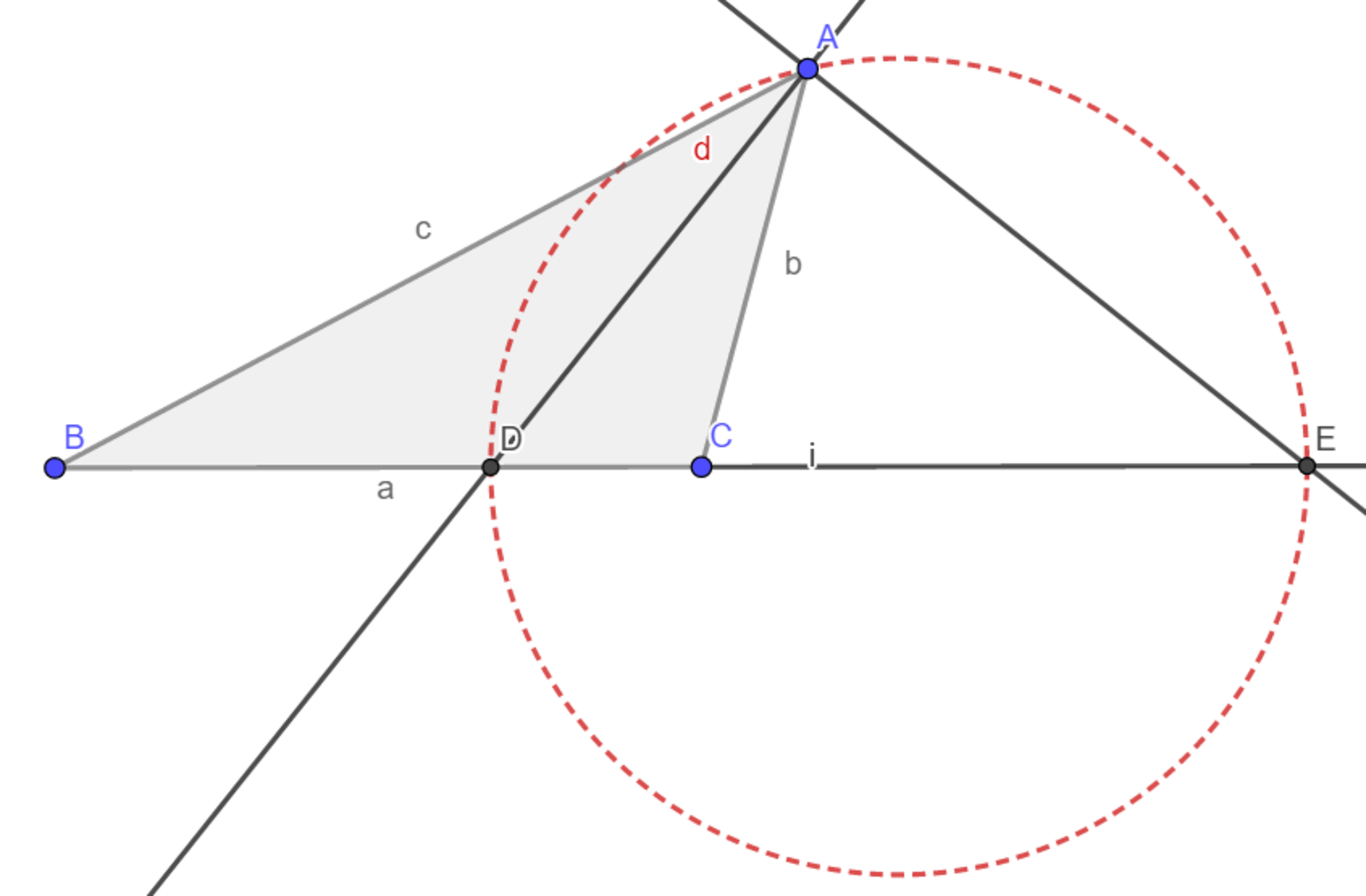 あ
あ
赤い点線の円が「アポロ二ウスの円」というやつです
角の二等分線を適用し、
下のリンクを参照してください
ウィキペディア
三角形$ABC$において、$∠A$の外角、$∠B,∠C$の内角の二等分線と対辺(直線)の交点をそれぞれ$X,E,F$とすると、$EF$は$X$を通る。
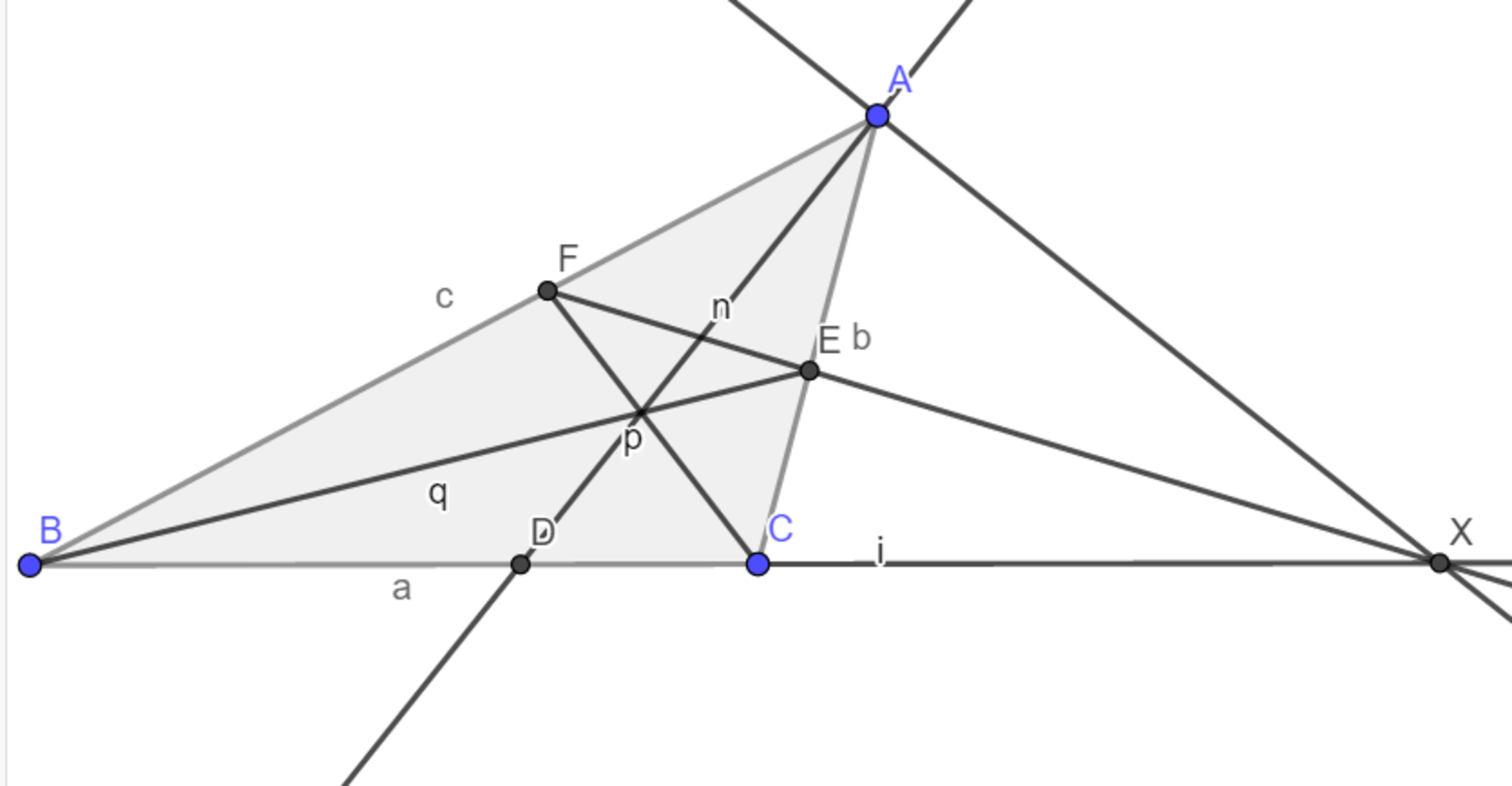 モナリザ
モナリザ
生意気な定理です(?)
$EF$と$BC$の交点を$X'$として、$X=X'$を示す。
$BX':CX'=BX:CX$を示せば十分である。(定理1より$X'$の可能性としては$D$もあり得るけど、$D \neq X'$でないと図が破綻する)
メネラウスの定理より$ \frac{AF}{FB}$$\cdot $$\frac{BX'}{CX'}$$\cdot$$\frac{CE}{EA}$$=$1
また内角の二等分線の定理から $\frac{AF}{FB}$$=$$ \frac{CA}{BC} $$,$$ \frac{CE}{EA} $$=$$ \frac{BC}{AB} $を代入して
$ \frac{CA}{BC}$$\cdot $$\frac{BX'}{CX'}$$\cdot$$\frac{BC}{AB}$$=$1$ \Longleftrightarrow $$\frac{BX'}{CX'}$$\cdot$$ \frac{CA}{AB} $$=$1$ \Longleftrightarrow $$BX':CX'=AB:CA$
最後に外角の二等分線の定理により$BX':CX'=BX:CX$が得られる。
三角形$ABC$の外心、九点心、垂心をそれぞれ$O,K,H$とすると、三点はこの順で一直線上に等間隔で並ぶ。
「九点円の定理」とまとめてスタイリッシュに示します
三角形$ABC$の各辺の中点をそれぞれ$M,N,L$、各頂点から各辺へ降ろした垂線の足を$D,E,F$とする。また$ABC$の外接円の半径を$R$とする。$▲ABE$$\backsim$$▲ACF$より、$AB$$\cdot $$AF$$=$$AC$$\cdot $$AE$、両辺を2で割ると$AN$$\cdot $$AE$$=$$AL$$\cdot $$AF$。方冪の定理の逆より$N,F,L,E$が同一円周上にあり、同様に$M,N,E,D$、$M,L,F,D$がそれぞれ同一円周上にある。$O,H$の中点$K$をとれば$MD,NE,LF$の垂直二等分線は$K$を通っているので、六点$D,E,F,M,N,L$は$K$を中心に、特に$M,N,L$を通ることから半径$R/2$の円上にあることが分かる。さらに$KH:OH=1:2$が成り立つことは、$H$は外接円($円O$)と円$K$の相似の中心であることを示している。相似比が$1:2$であることから、残りの三点はこの事実から従う。
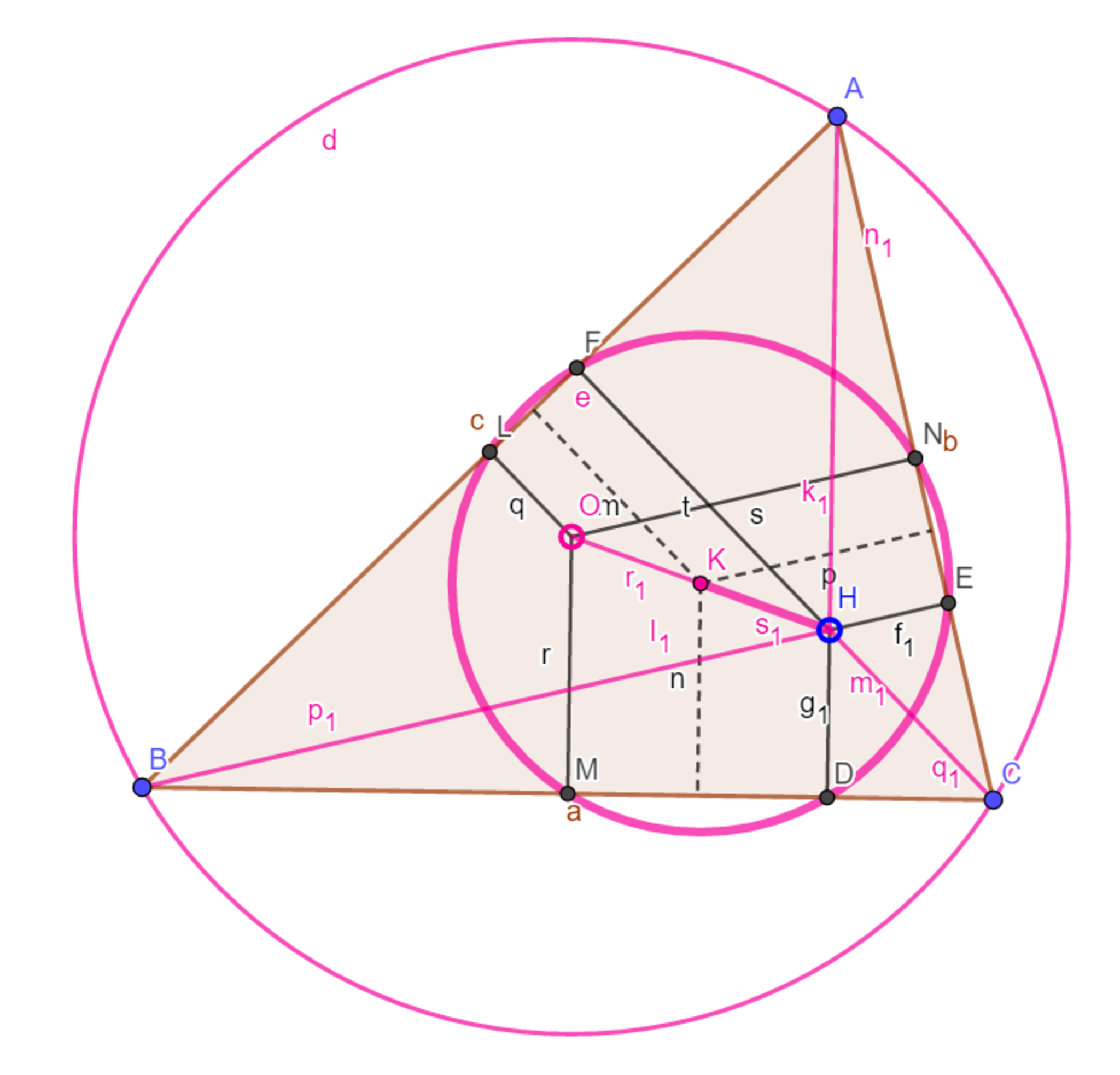 図
図
有向角について
有向角について、こちらの記事がとても参考になりました(参考文献の項に改めて添付しています)
https://mathlog.info/articles/2956
これより下を読むにあたって、有向角($\measuredangle $)について知らない人も証明を読む分には普通の角度($∠$)の記載と変わらないと思うので、そのつもりで読んで分かると思います。
($-\measuredangle ABC=180°-\measuredangle ABC $だけ抑えればいいと思います。)
問題
以下の図において、$O_1,I,S$はそれぞれ三角形$ABC$の外心、内心、$∠A$内の傍心である時、$O_1S$$ \bot $$EF$を示せ。
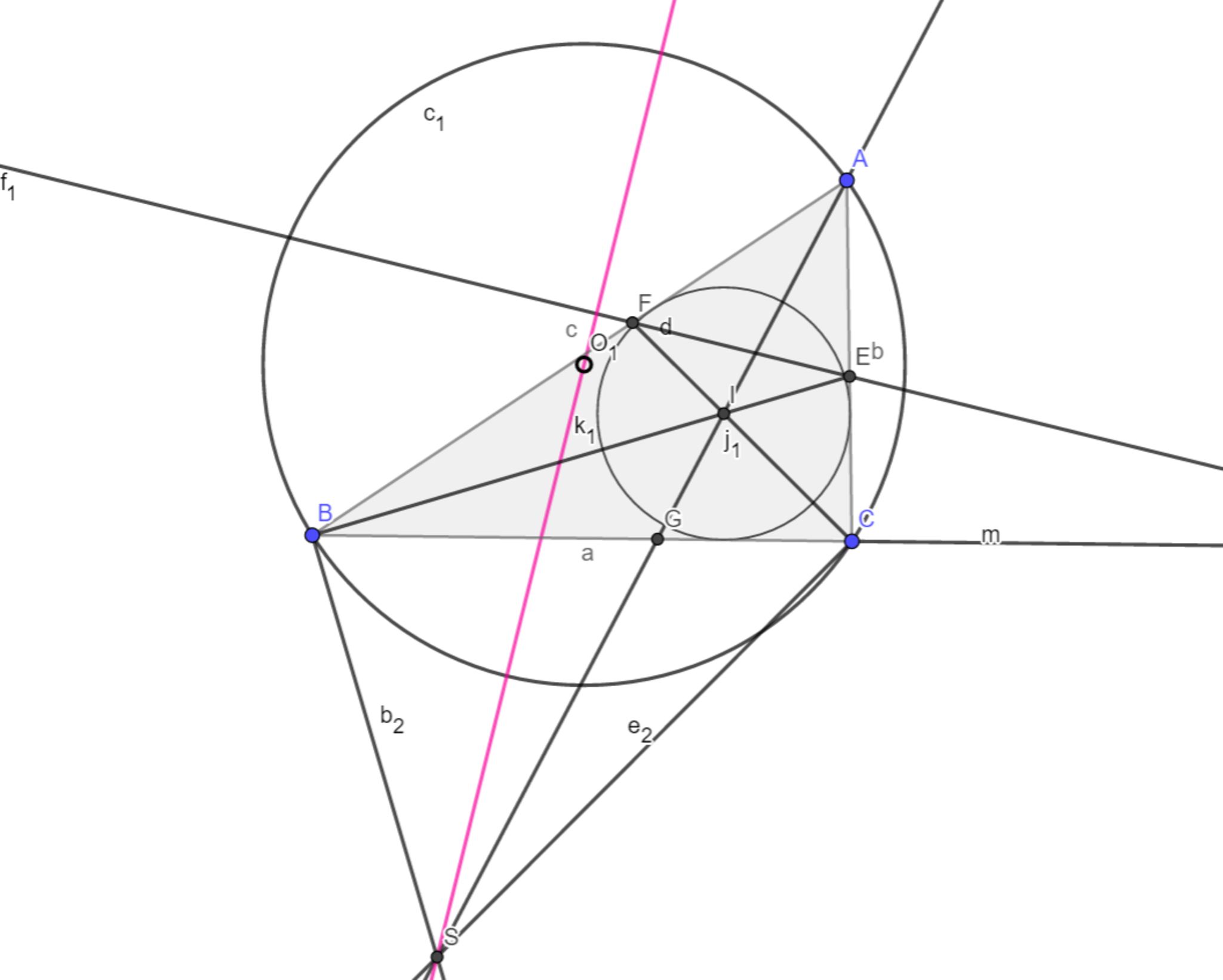 図1
図1
勝手に傍心関係の有名問題と認知してますが、主張が綺麗でしかも難しめの良問です。別の問題を解いた時に、この問題も同時に解けるかたちになったので、その問題に触れながらの証明になりますが、そんなに遠回りはしてないとおもいます。(証明では補題として使ってます)
証明
(ここからの図で$I$は内心、内接円の接点を$D,H,J$としています)
補題の証明
以下の図において、点$I´$は内心$I$の直線$JH$を軸に対称な点とする時、$DI’$$ \perp EF$。
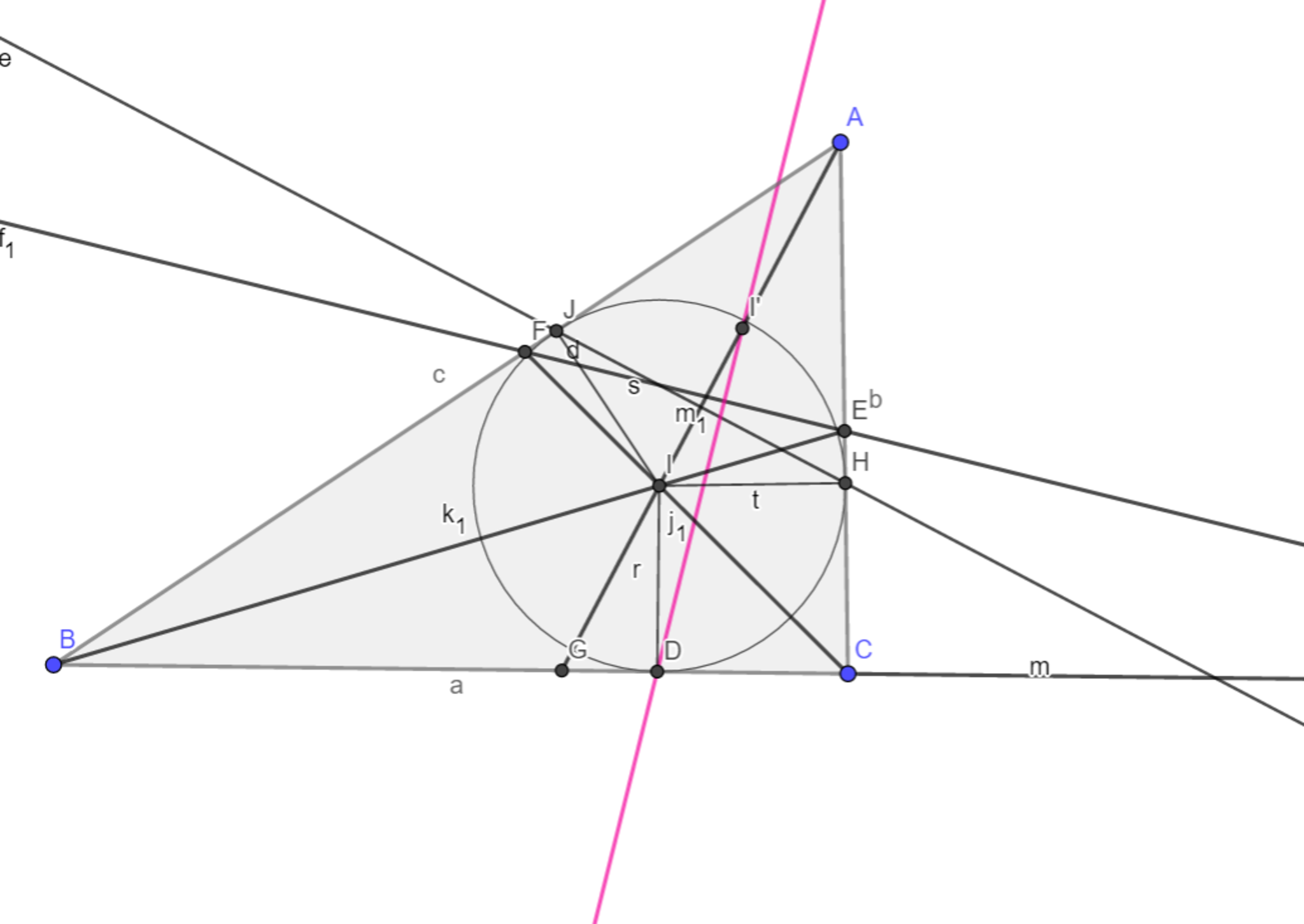 図
図
ごち数のProbrem#93(BMO 2018 SLP G2)と主張が同じ問題です。元の問題での三角形ABCを三角形DHJとして見ています。このサイトにも解法は書いてありますね。(主題の問題の証明も途中で用いられてます) (また、元の問題では三角形DHJの九点心とDの直線となっていると思いますが、後で示すように同じ直線です)
ごち数#93のページ
$[1] STEP.1:$図6において$IX$が線分$KR$の中点$P$を通る。
(これより下では、$X$は上の定理2と同じ、$JH$と$EF$の交点を$K$、$JH$と$IA$の交点を$Q$、$JH$と$AB$の交点を$R$としています)
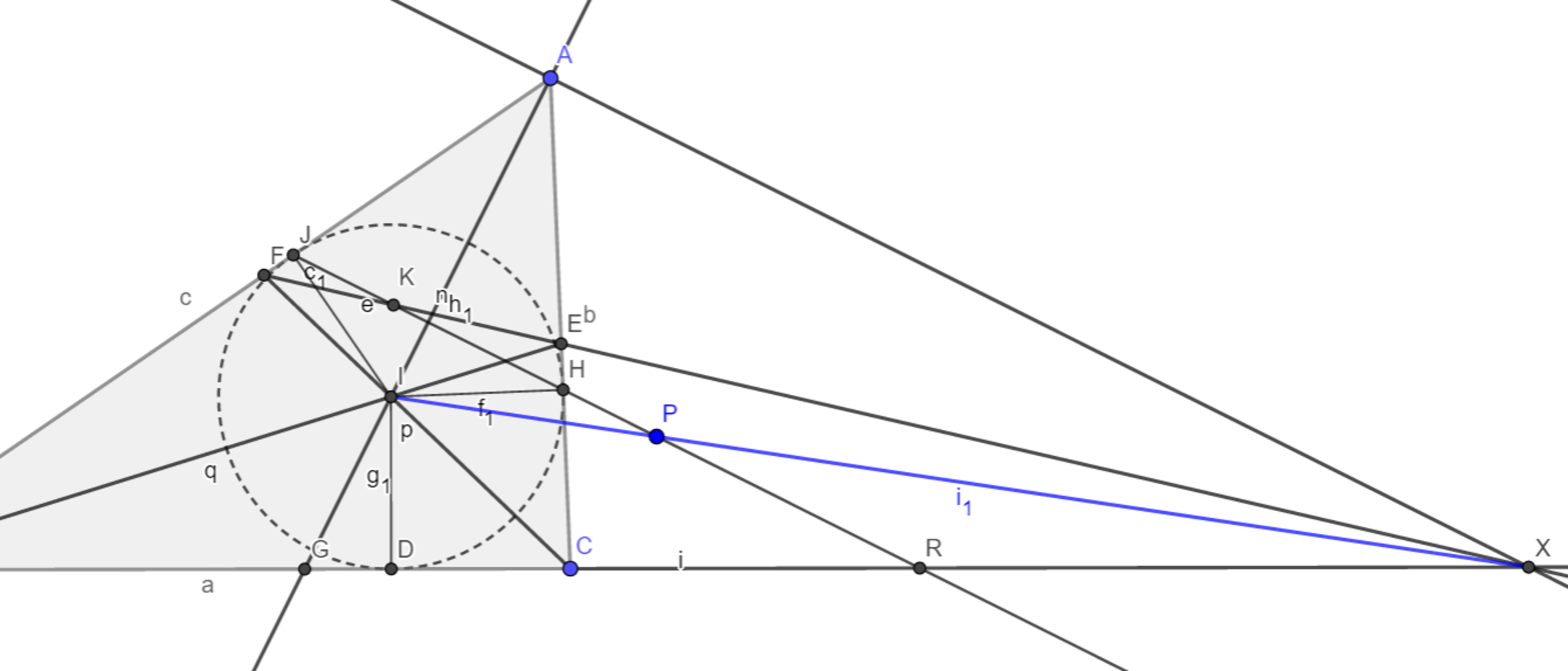 図
図
図7において$NI=IO$つまり$NL=MO$をまず示す。
※点線は$I$を通る$AI$に垂直な直線、$N,L,M,O$は点線とそれぞれ$EF,AB,AC,BC$の交点
$AX$と点線がどちらも$AI$と垂直なので平行である。
三角形$NFL$と三角形$XFA$、三角形$CMO$と三角形$CAX$の相似において、$LF:FA=CM:CA$を示せば良い(図7)。$AI$を軸に$C$と対称な点$C'$をとれば、$C’$は$AB$上にあり、また三角形$C'IF$において内角、外角の二等分線と$C'F$の交点がそれぞれ$L,A$になっているので、定理1と$CM:CA=C'L:C'A$であることから、$LF:CM=FA:CA$$ \Longleftrightarrow $$LF:FA=CM:CA$を得る。
よって図8のように、$KR$と点線が$AI$と垂直で平行であるから$NO$の中点が$I$と分かったことにより$KR$の中点$P$で$IX$は交わっていると分かる。$STEP.1$終
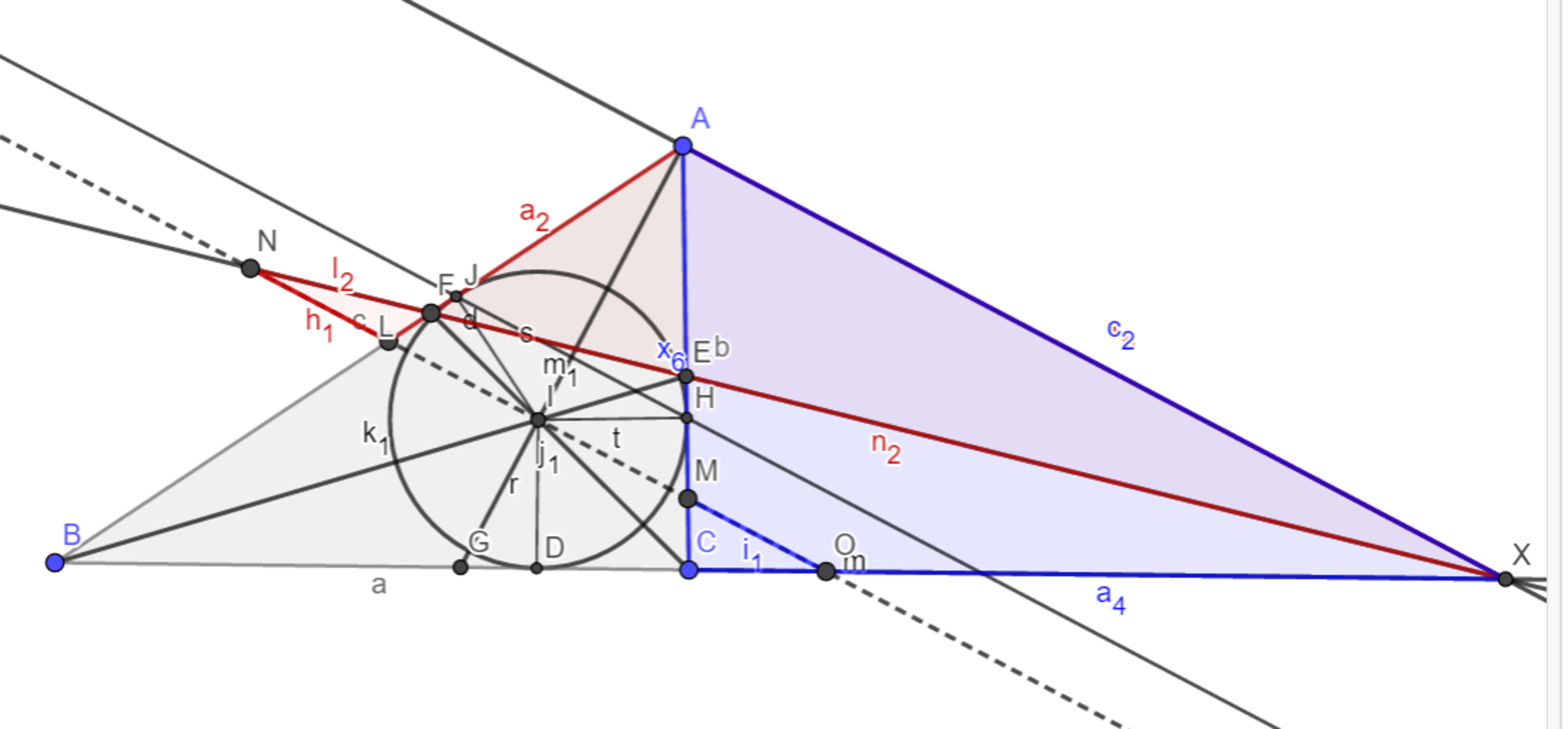 図
図
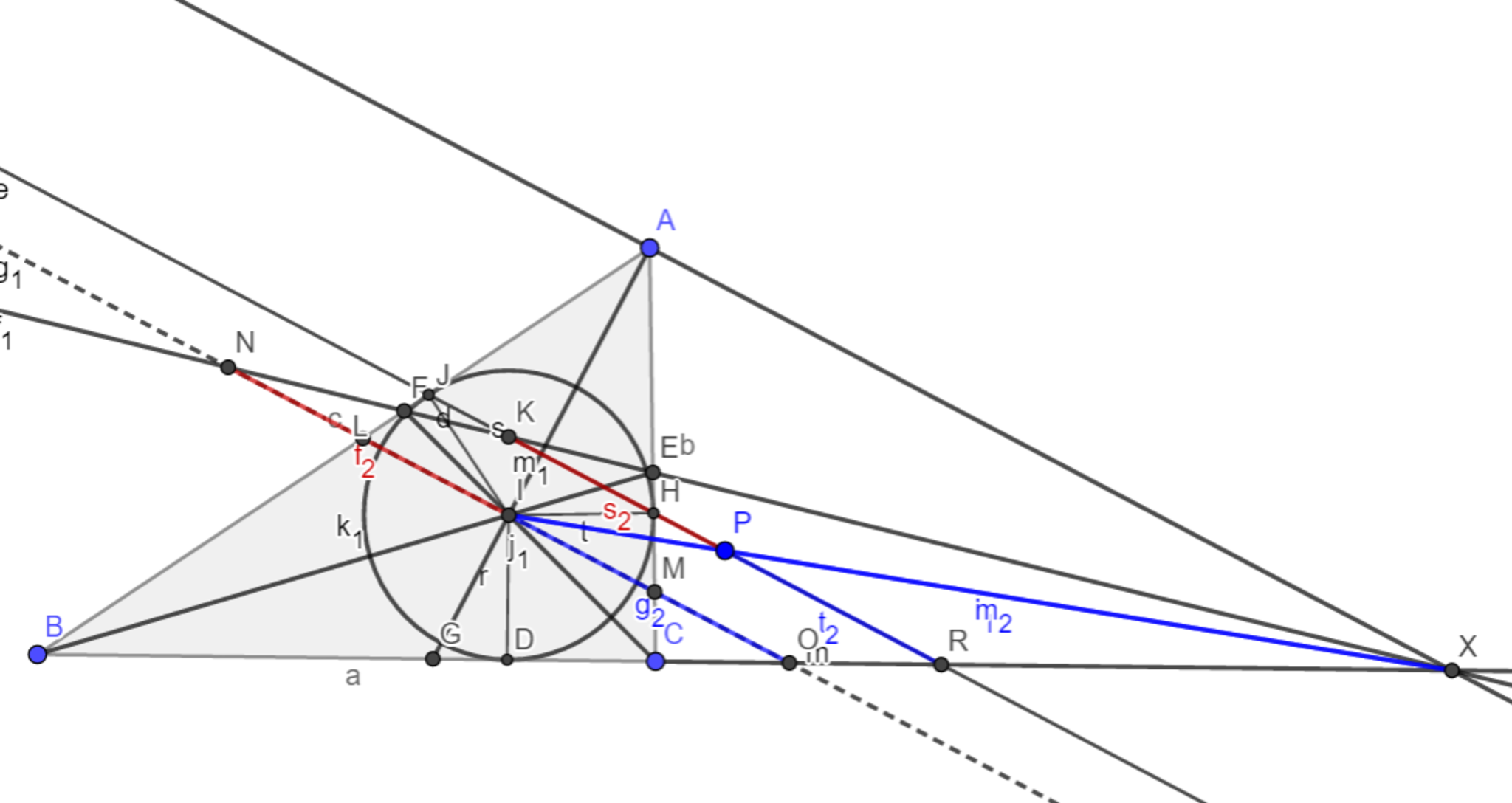 図
図
次に相似による議論で考察をします。
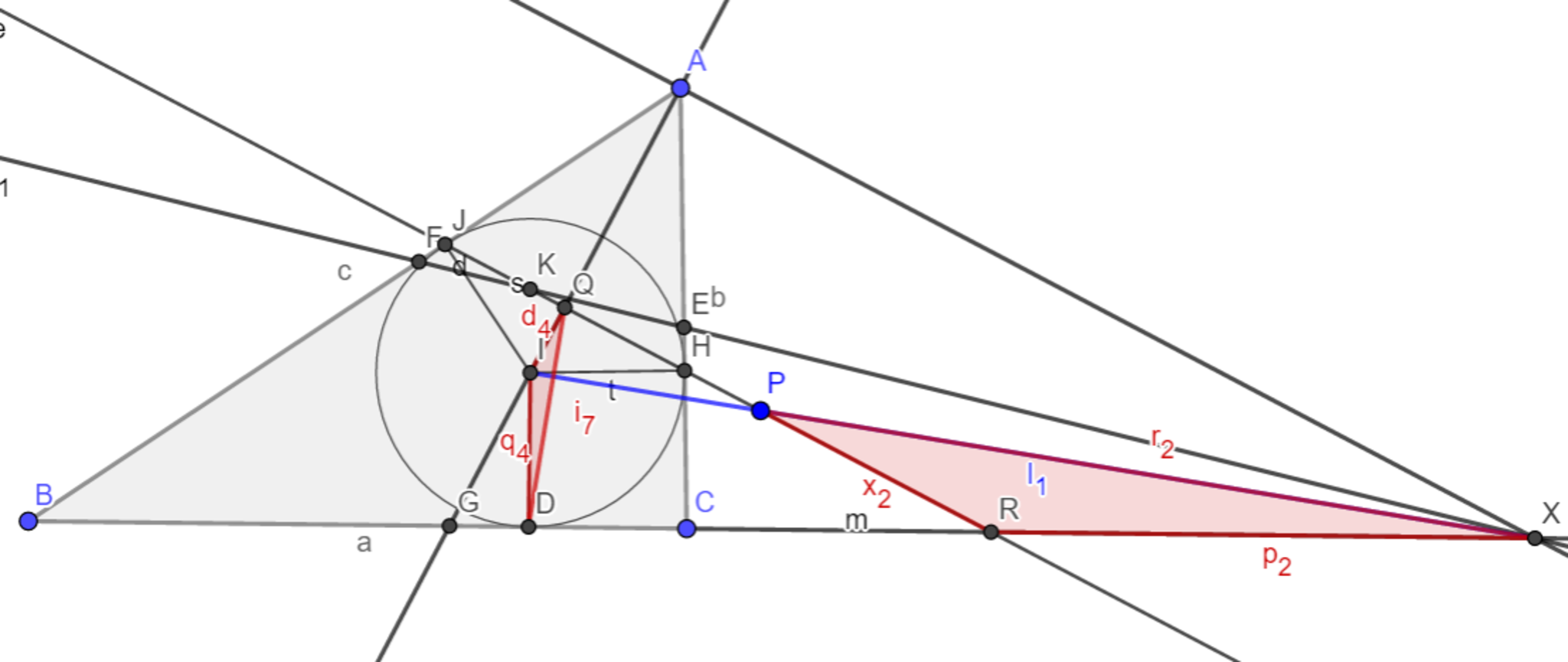
$[2] STEP.2:$図9において向きが正の相似(回転相似)$▲QID \backsim ▲PRX$が成り立つ。
 図
図
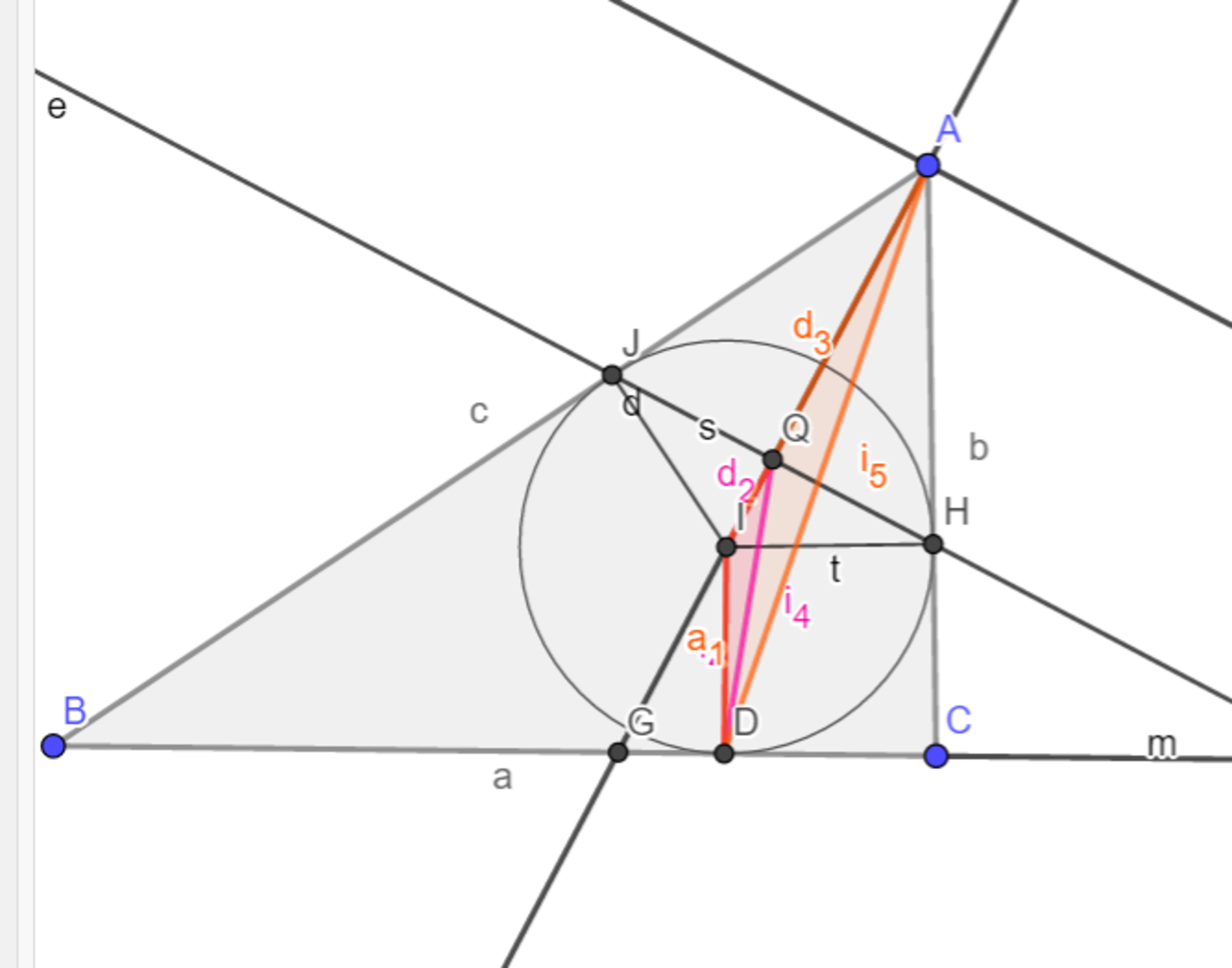
図10において$▲IJQ$$\backsim$$▲IAJ$より$IQ \cdot IA=IJ^{2} $。$IJ=ID$より$IQ \cdot IA=ID^{2} $かつ$ \measuredangle DIQ=\measuredangle DIA$ $\Longleftrightarrow$ $▲IQD$$\backsim$$▲IDA$。
 図
図
(図11$,$12)
四点$I,D,R,Q$、$I,A,X,D$において$\measuredangle IDR =\measuredangle IQR=90°$$,$$ \measuredangle IAX=\measuredangle IDX=90°$より$▲IQD$$\backsim$$▲IDA$の相似において$R,X$は対応しているので、四点$I,D,R,Q$、$I,A,X,D$は相似になっている。
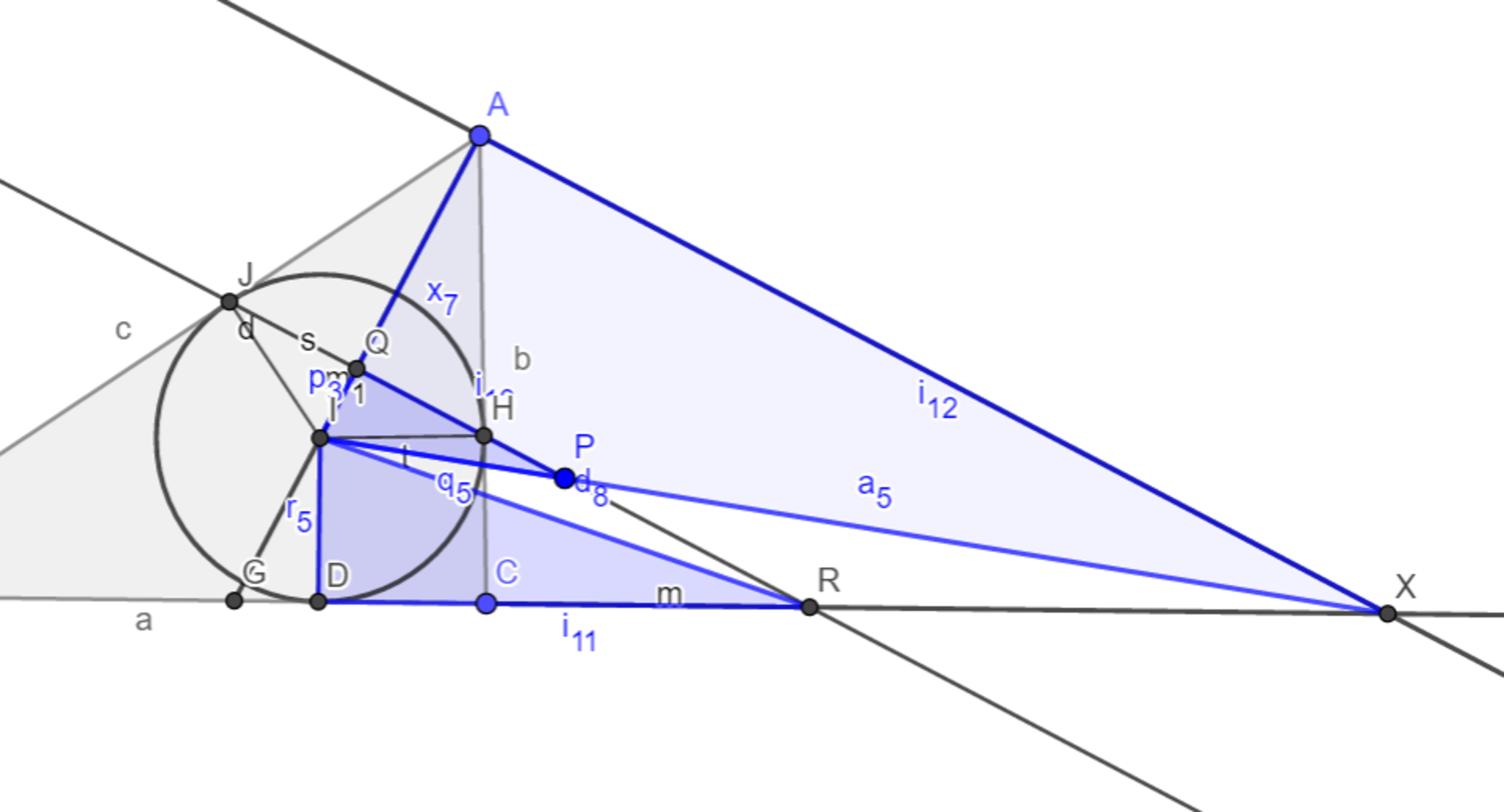
これにより$▲IRD \backsim ▲IXA$(図11),$▲IRQ \backsim ▲IXD$(図12)。さらに$QP$と$AX$が平行なので$▲IXA\backsim▲IPQ$より、まとめると
$\therefore ▲IRD \backsim ▲IPQ $,$▲IRQ \backsim ▲IXD$。(それぞれ向きが負の相似である)
 図
図
 図
図
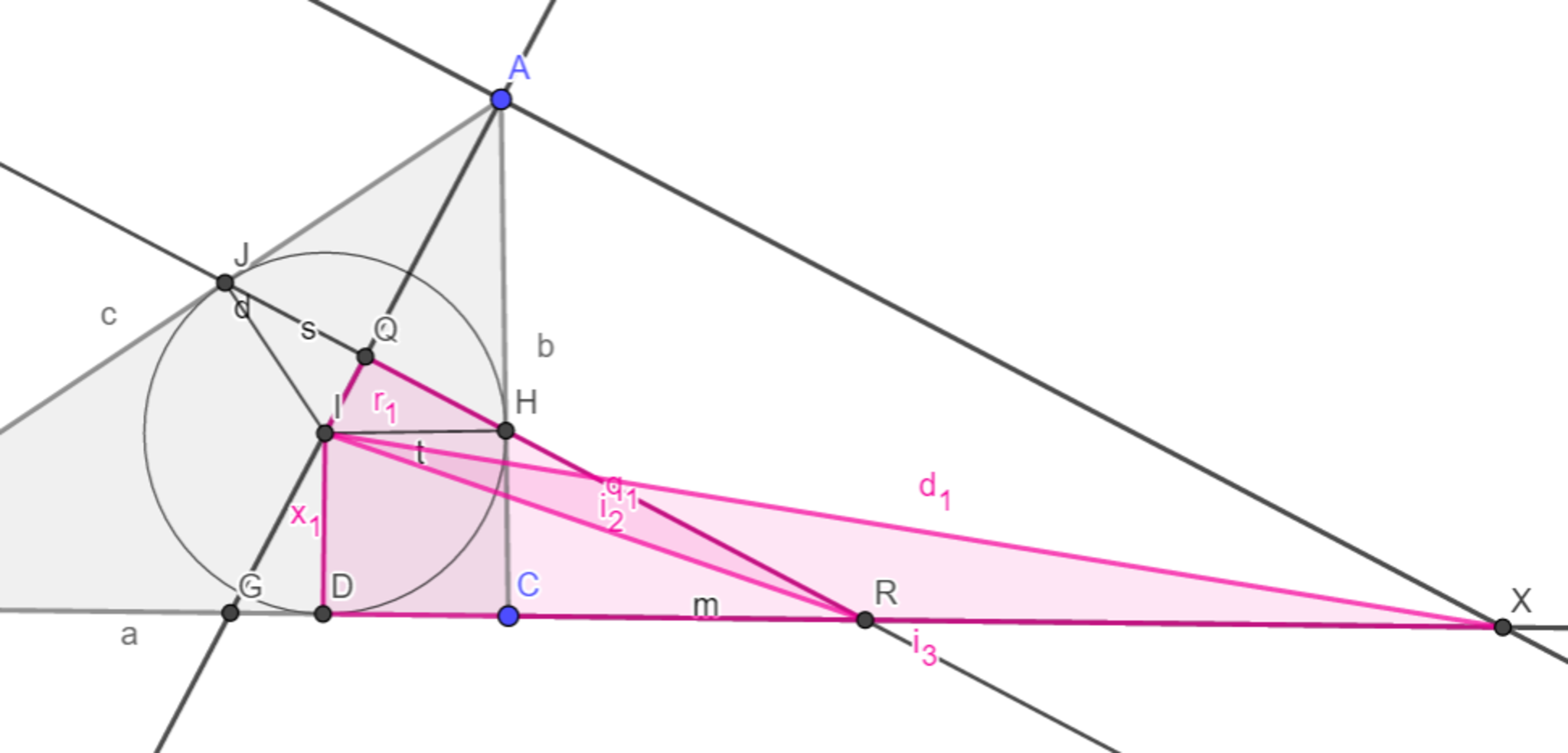
これは、$▲IRQ \backsim ▲IXD$の相似において$P$と$R$がそれぞれ対応していることを示している。(図13)(注)
よって$IQ:RP=ID:XR$つまり$IQ:ID=RP:XR$が分かり、また$\measuredangle IDR =\measuredangle IQR=90°$ なので$\measuredangle QID=\measuredangle QRD=\measuredangle QRX$より$▲QID\backsim▲PRX$が従う。 $STEP.2$終
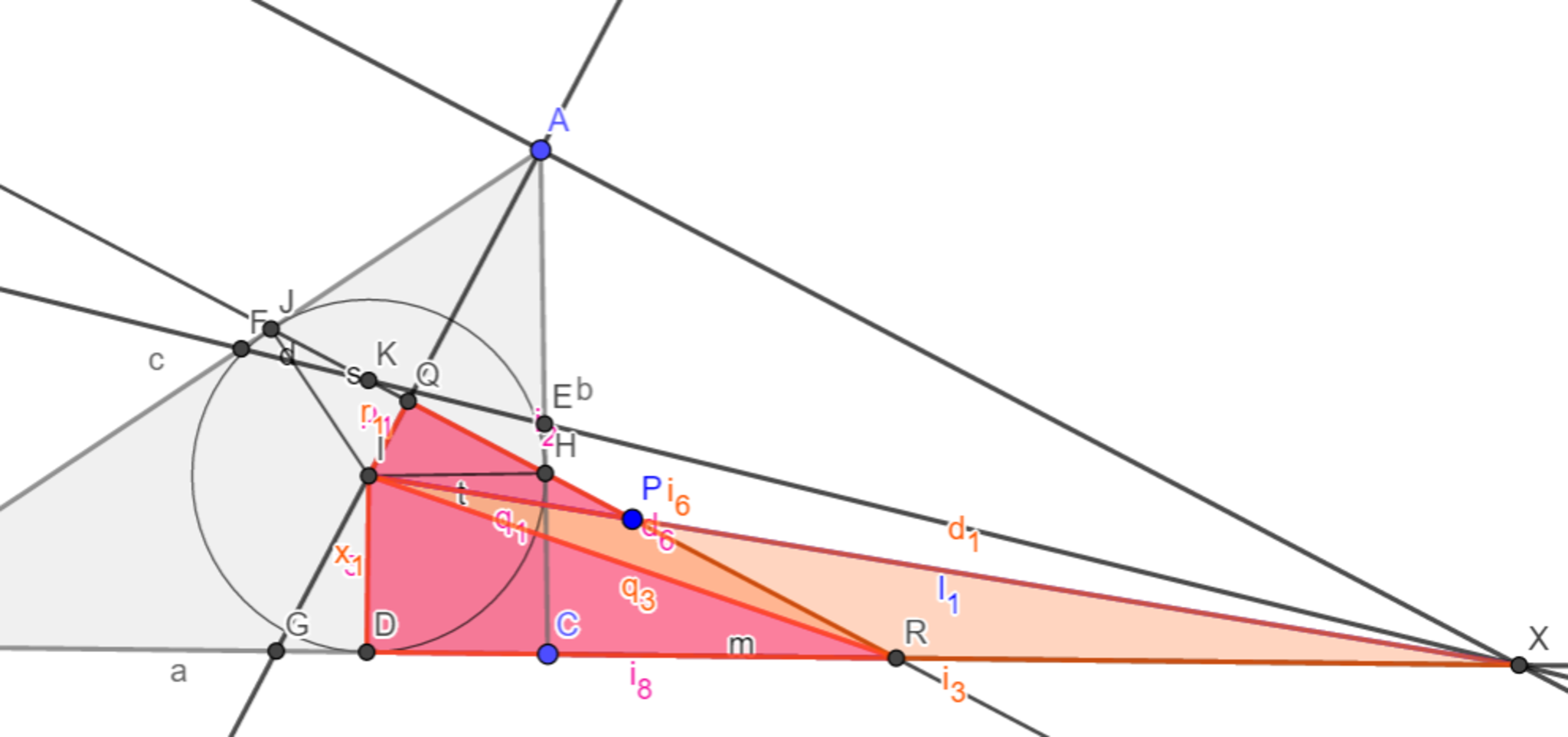 図
図
 図
図
$[3]仕上げ$
$STEP.1,STEP.2$より、内心$I$の直線$JH$を軸に対称な点$I’$をとれば、$IQ:II’=RP:RK=1:2$なので$▲I’ID\backsim▲KRX$が成り立つ。この相似は正の相似(回転相似)なので、対応する辺の直線同士の成す角度は等しい。$I´I \perp KR, ID \perp RX$は自明より、$DI’\perp KX(=EF)$が分かる。 $(証明終)$
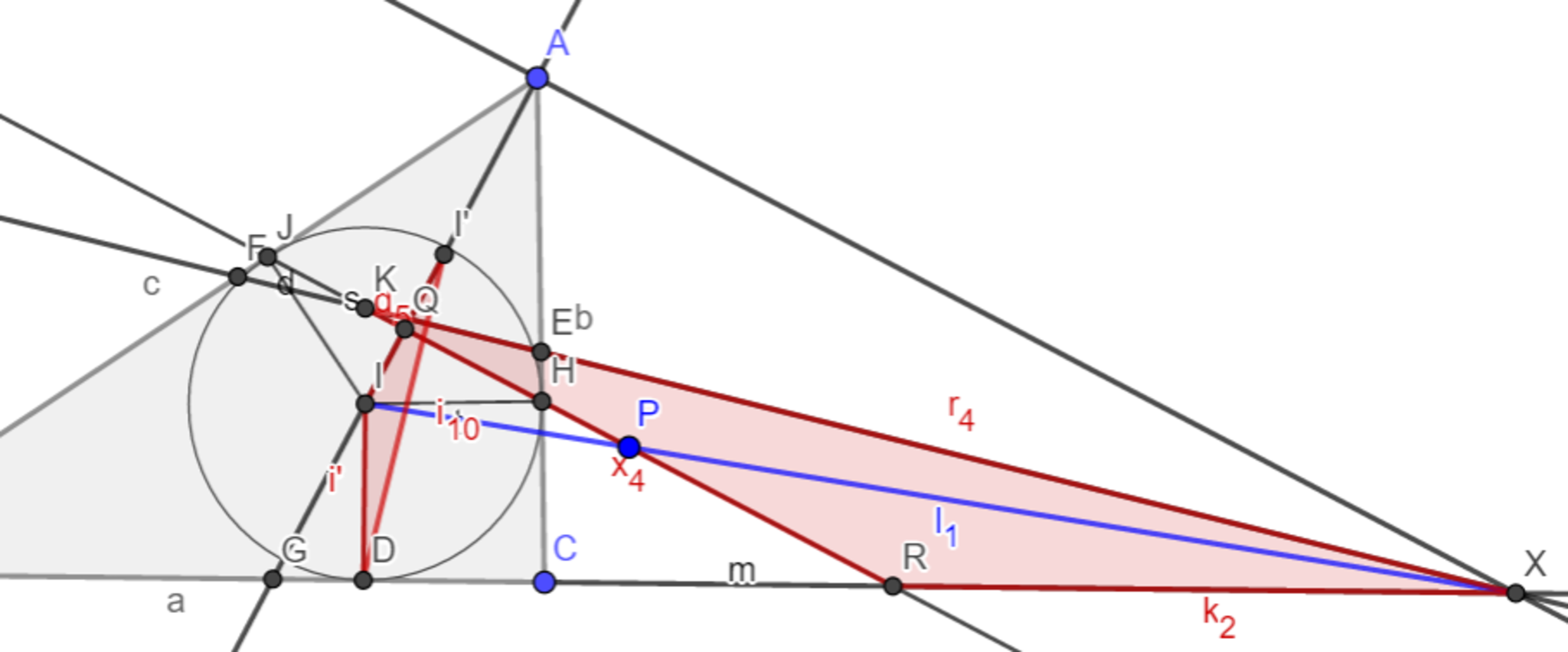 図
図
(注)の整合性について:※これは追記です
ここは不安要素があるかなと感じたので
六点$I,D,X,P,Q,R$について、以下の条件を満たすモデルを考えれば、どんな場合でも成り立つはずです。いずれにせよ自明な事ではないかもしれません
- $D,R,X$と$P,Q,R$がそれぞれ一直線
- $I$について、$ID$と$IQ$がそれぞれ上の2本の直線に直行している
- $▲IRD \backsim ▲IPQ , ▲IRQ \backsim ▲IXD$であり、それぞれ直角三角形の負の向きの相似
三角形$ABC$において外心$O$と$BC$に対して対称な点を$O'$、九点心を$K$として、$A,K,O'$は同一直線上にある。
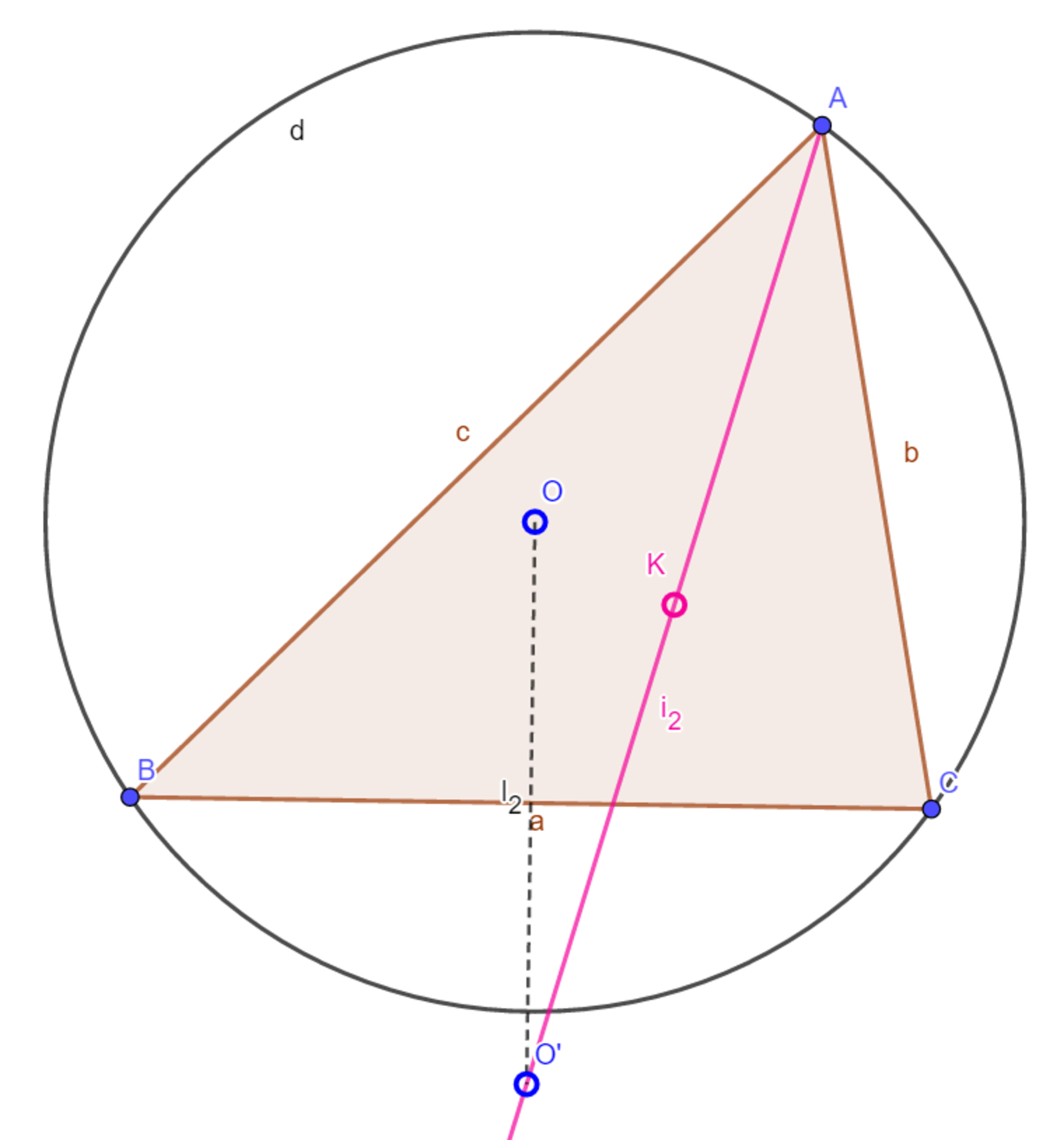 図
図
これはほぼ構図で示せます。
垂心を$H$、$AH$と$BC$、外接円との交点をそれぞれ$D,T(\neq A$)とする。$ \measuredangle BHC=-(\measuredangle CBH + \measuredangle HCB)=-( \measuredangle HAC + \measuredangle BAH)=- \measuredangle BAC =\measuredangle CTB$
であり、$HT \perp BC$より$HD=DT$が成り立つ。よって$T$は$H$と$BC$を軸に対称だから、$OA=OT=O'H$が成り立ち、
また$ \measuredangle OAT=\measuredangle ATO= \measuredangle OHT$ より $AO /\!/ HO'$
であるから四角形$AOO'H$は平行四辺形である。
定理3より$K$は$OH$の中点なので、$AO'$は$K$を通っている。$(証明終)$
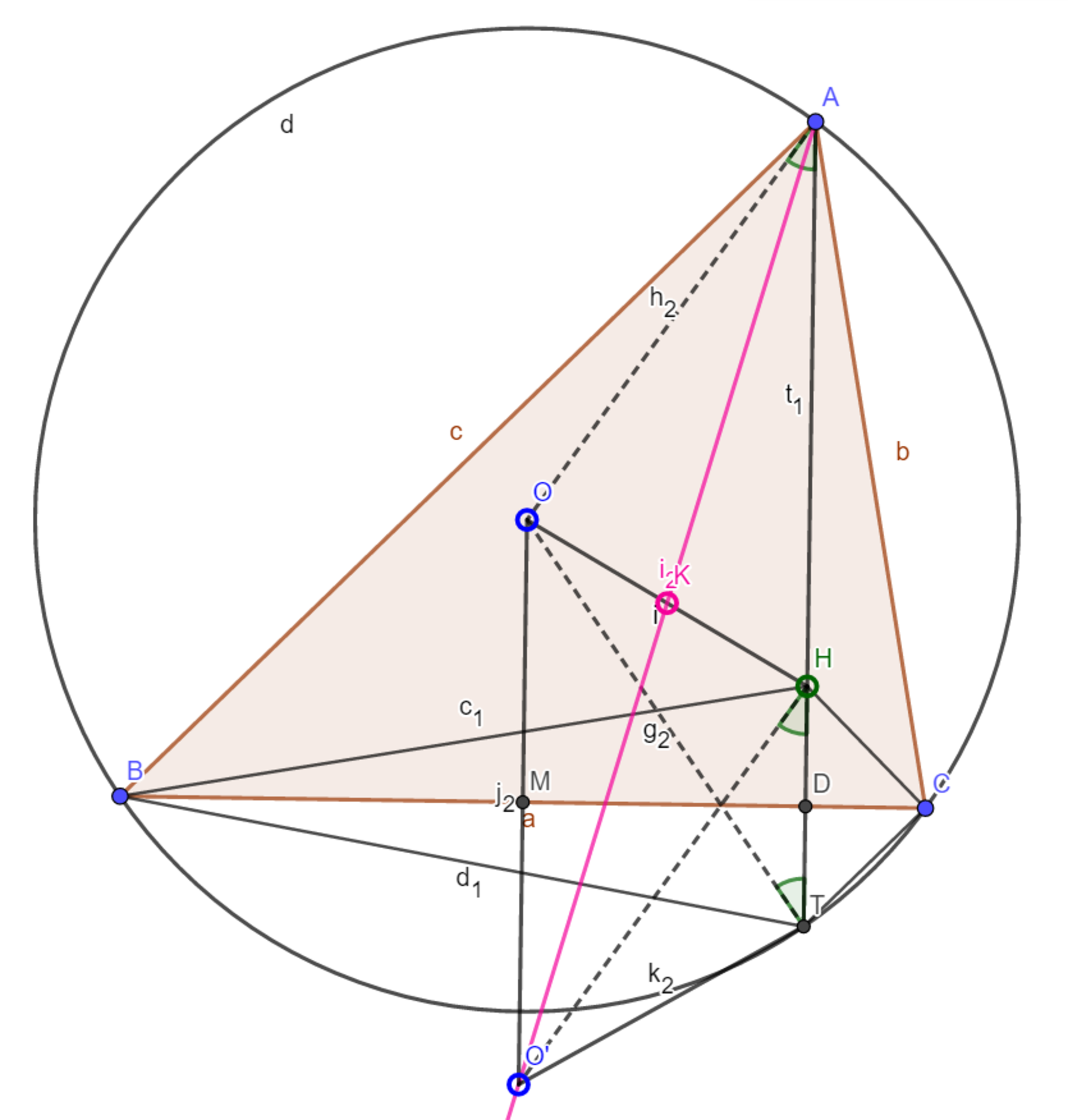 図
図
これで補題の証明は完了しました。あとは補題から本題へとつなげます。
本題の証明
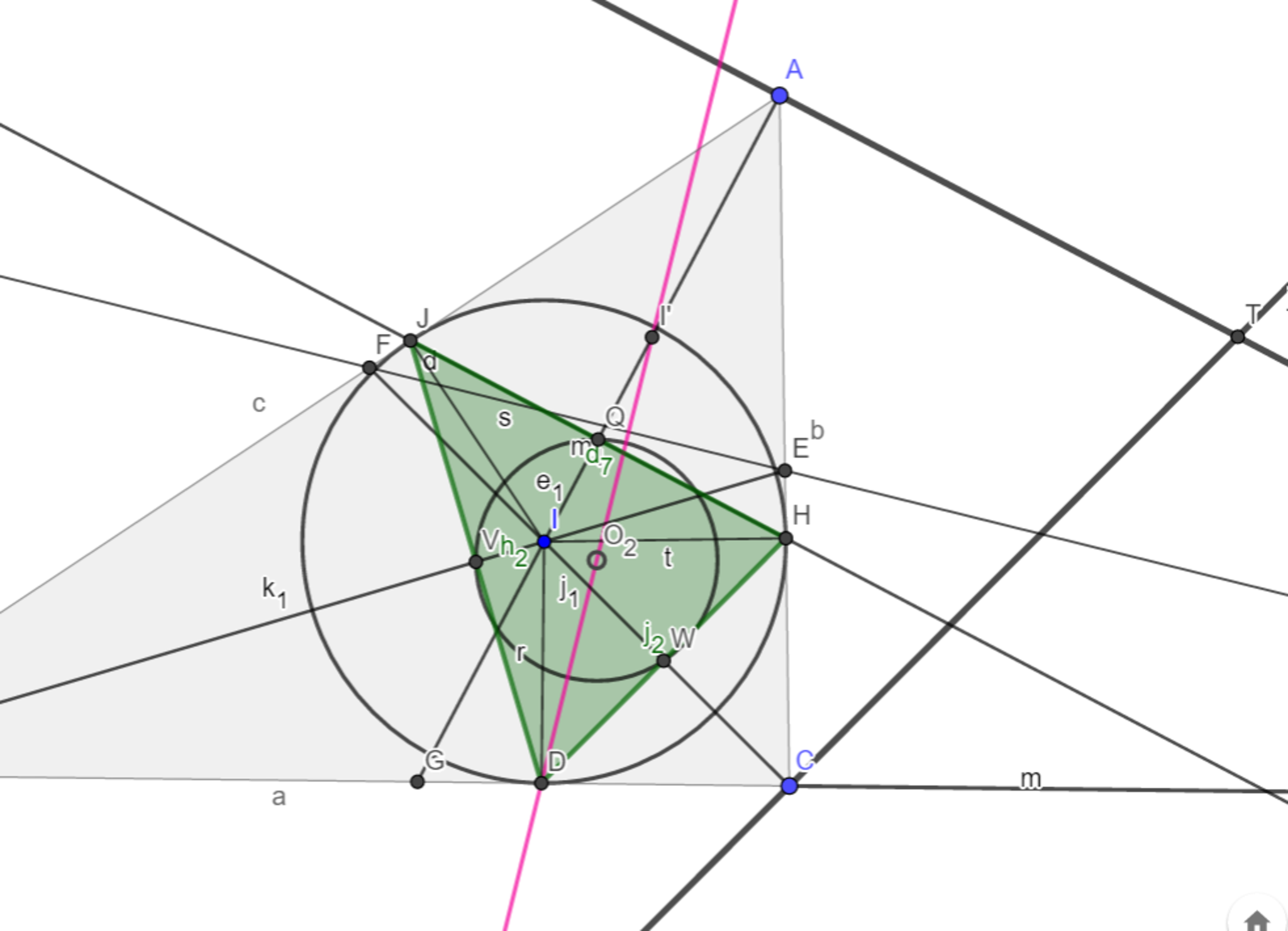
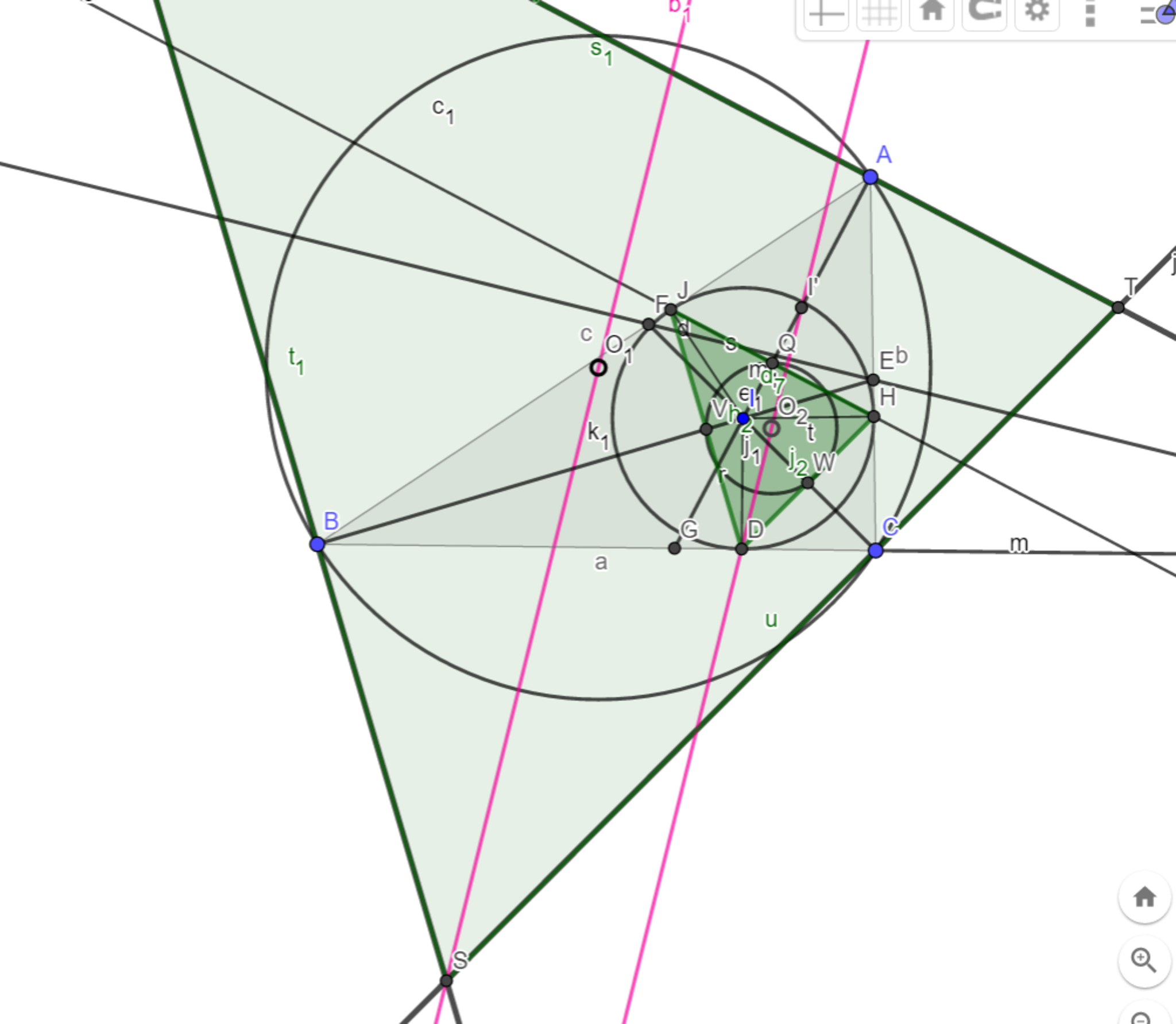
補題5を補題4の三角形$DHJ$に適用すると、外心が$I$なので三角形$DHJ$の九点心を$O_2$とすると$直線DI’=直線O_2D$である。(☆)(図18)
三角形$DHJ$の傍心をそれぞれ$S,T,U$とすると$HJ,TU$、$JD,US$、$DH,ST$はそれぞれ$AI,BI,CI$と直行してるため並行である。よって三角形$DHJ$と三角形$STU$は同じ方向に拡大縮小した相似関係にある。
三角形$STU$において$I$は垂心であることはすぐに分かるが、定期3で示した通り九点円は「各頂点から各辺へ降ろした垂線の足三点」を通るので、三角形$DHJ$の外心$O_1$が三角形$STU$における九点心にあたる。
つまり三角形$DHJ$と$STU$の相似において、$O_2$と$O_1$$,$$D$と$S$がそれぞれ対応しているので、$O_2D$は$O_1S$に対応している(図19)。よって☆ の事実も兼ねて$DI’=O_2D /\!/ O_1S $となる。
補題4より$DI’ \perp EF$なので、$O_1S \bot EF$を得る。 $(証明終)$
 図
図
 図
図
まとめ
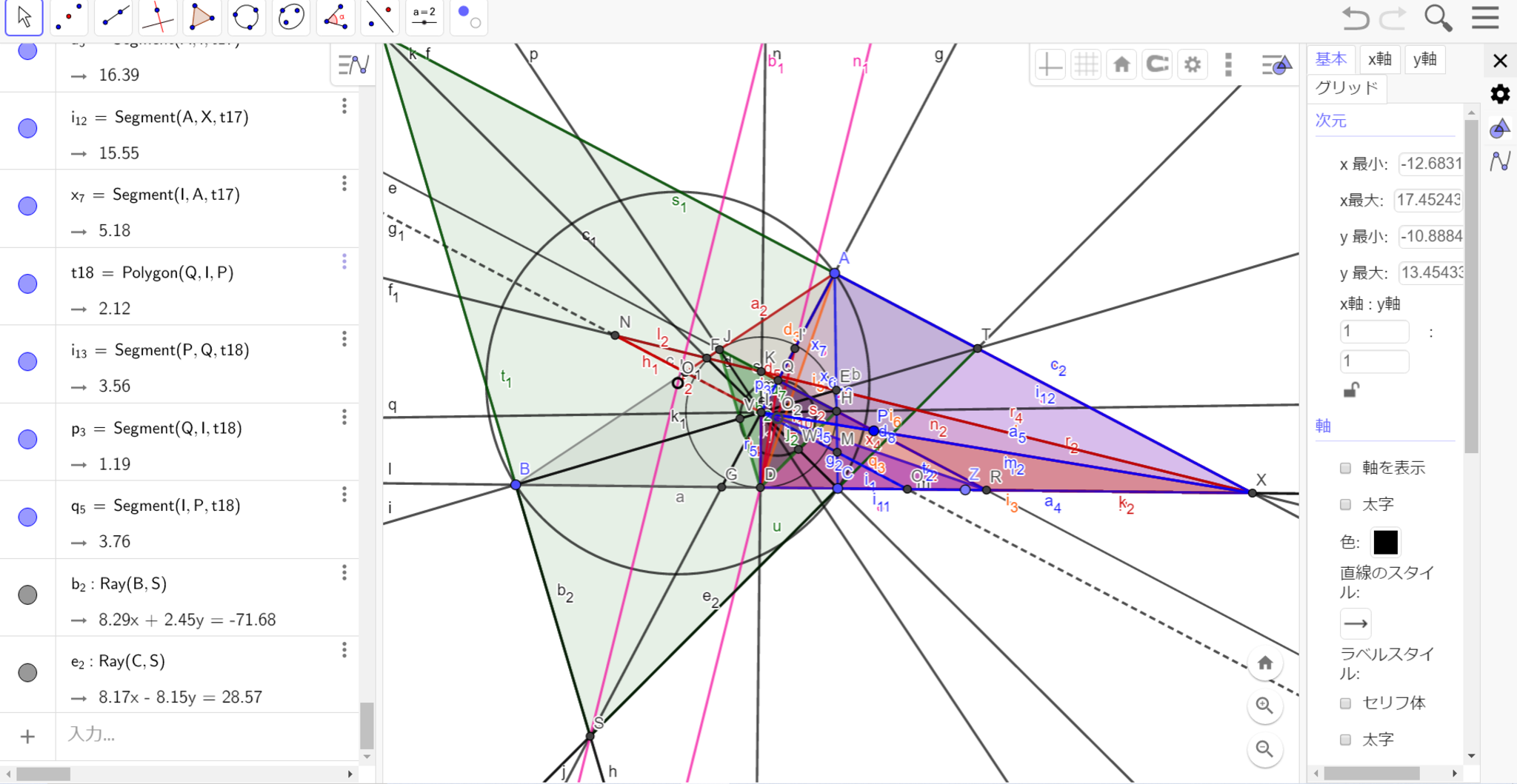 激オモまとめ画像
激オモまとめ画像
忙しい人のためにまとめるとこんな感じですね
参考文献
ごち数(補題4を知った経緯) https://gochisuu.netlify.app/problems/93/
本題を知った経緯 https://su-hai.hatenablog.com/entry/2017/07/10/190011
誤植を見つけたら直ちにご報告お願いします。