オリジナル図形問題 with 円 and 楕円 and レムニスケート
イントロダクションは長めにすればよいと聞きました
タイトルの通り、今回は円と楕円とレムニスケートが登場する図形問題である。だが、円と楕円はともかく、「レムニスケートって何？」という読者もいらっしゃるだろう。何か難しそうな響きの単語であるが、一応知らない読者のために簡単な説明をする。知っていたら読み飛ばしていただいて構わない。
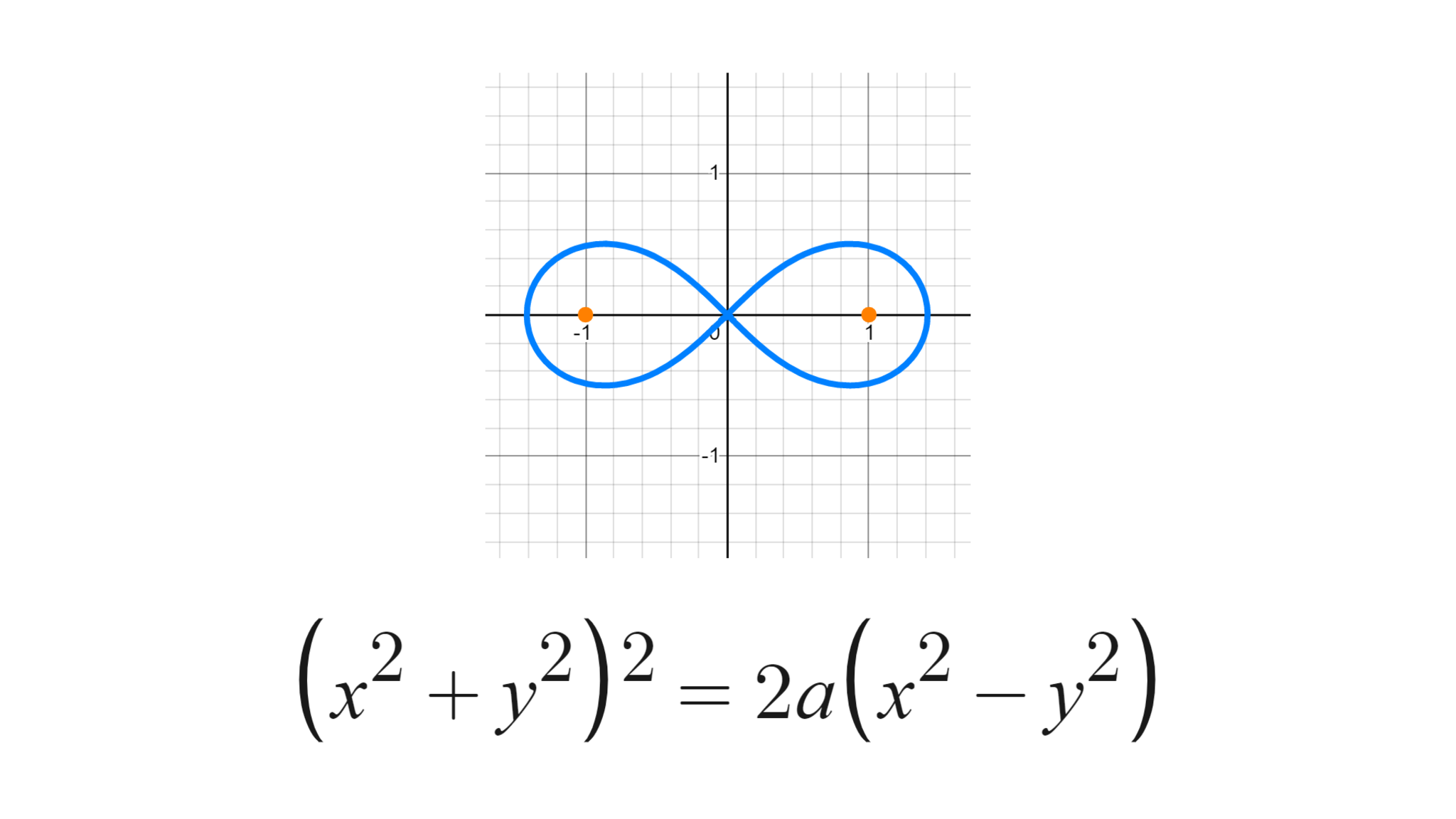どう見ても無限大マーク(∞)
レムニスケートは、正の実数$a$を用いて
$$\begin{eqnarray} \left(x^{2}+y^{2}\right)^{2}=2a\left(x^{2}-y^{2}\right) \end{eqnarray}$$という方程式で表される4次曲線である(上の図は$a=1$の場合)。
2点$(\pm \sqrt{a},0)$を、レムニスケートの焦点と呼ぶ(上の図の橙色の点)。なお、2つの焦点$(\pm \sqrt{a},0)$からの距離の積が$a$になる点の軌跡としても、同じレムニスケートを描くことができる。(参考： Wikipedia )
それにもかかわらず、レムニスケートを題材にした幾何は非常に非常に非常に非常に非常に非常に非常に非常に非常に非常に少ない。先述の通り、円の出てくる幾何はあまりにも多いのに。ほんの少し方程式が難解になっただけでこの仕打ち。どう考えても不公平だ。
……とレムニスケート氏から悲痛な相談を受けた私は、彼の無念を晴らすべく、レムニスケートが持つ様々な性質を調べた。既知の性質が殆ど無く、自力で試行錯誤を繰り返し苦節1週間強。結果、本記事の最後に記す性質に辿り着けたので、それを活かした自作問題を紹介する。
問題紹介前にブラウザバックした人がいると聞きました
見た目が綺麗(感じ方には個人差があります)
すぐ下に解答があるので、自力で考えたい方はここでスクロールをストップするように。
解答は行間に高密度の議論を詰め込むべきだと聞きました
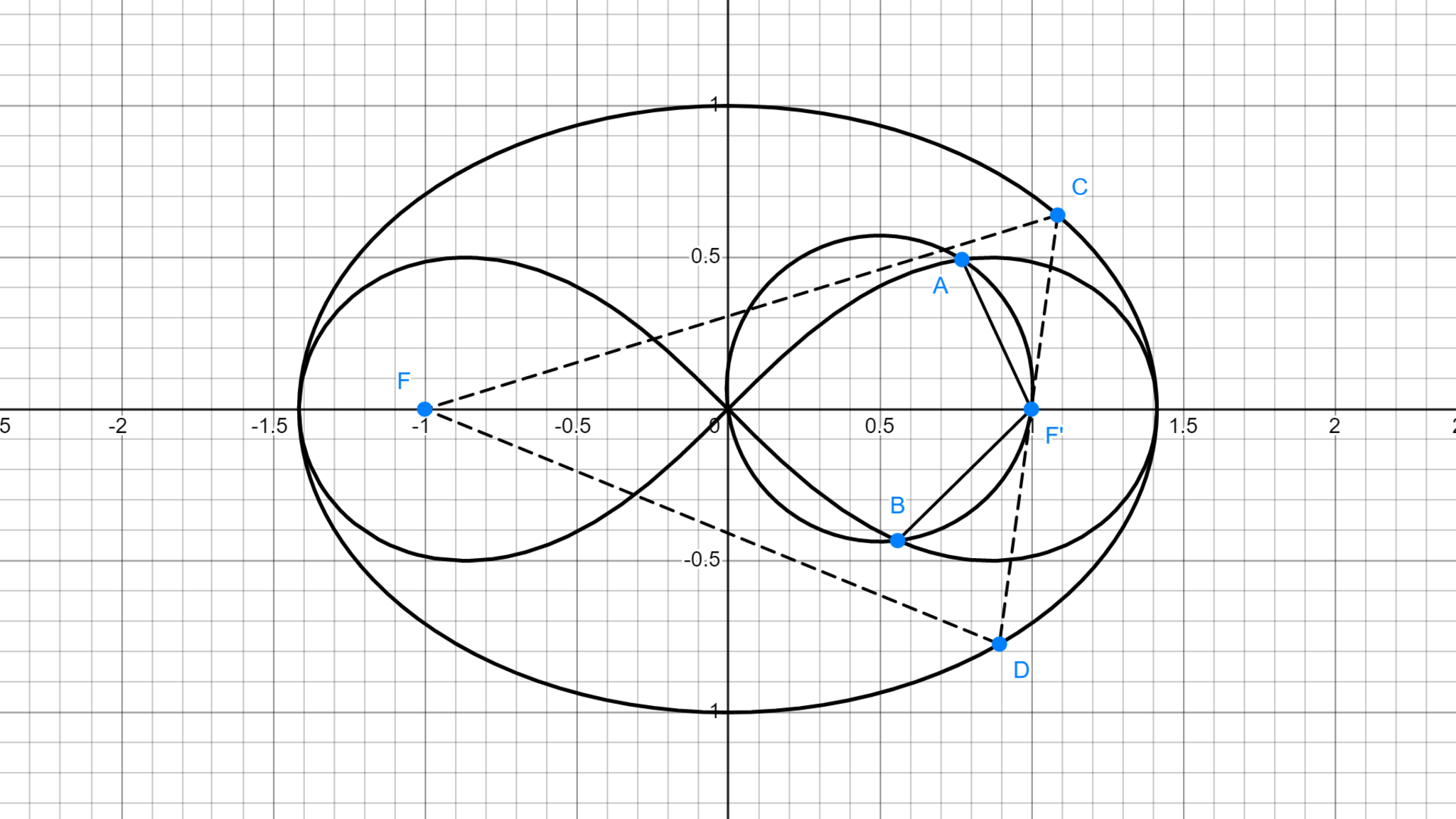レム睡眠(レムニスケートを考察しながら取る睡眠のこと)
$$ \epsilon : x^2+2y^2=2, \quad \lambda : \left(x^{2}+y^{2}\right)^{2}=2\left(x^{2}-y^{2}\right)$$
と表せる。
$\gamma$の中心の座標を$\left(\dfrac{1}{2},\dfrac{\tan\left(a\right)}{2}\right)$とおくと$\left(0^{\circ}< a<45^{\circ}\right)$、$\gamma$の式は
$$ \gamma : \left(2x-1\right)^{2}+\left(2y-\tan\left(a\right)\right)^{2}=\dfrac{1}{\cos^{2}\left(a\right)}$$
である。$F'$から引いた$\gamma$の接線を$l$とすると、その式は$l: y=\dfrac{x-1}{\tan\left(a\right)}$となる(ここまで証明略)。
$$\begin{eqnarray} \left\{\begin{array}{l} A'\left(\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1},\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}\right) \\ B'\left(\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1},\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}\right) \\ C'\left(\dfrac{2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)},-\dfrac{\left(\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}\right) \\ D'\left(\dfrac{2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)},-\dfrac{\left(\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}\right) \end{array}\right.\end{eqnarray}$$
各々の式に代入して計算することにより、2点$A',B'$は$\lambda$および$\gamma$上に、2点$C',D'$は$\epsilon$および$l$上に存在することが示せる。よって、$A$と$A'$、$B$と$B'$、$C$と$C'$、$D$と$D'$はそれぞれ一致する($x$座標の大小関係を考慮した))。
$$\begin{eqnarray}
\dfrac{4\sqrt{2}\cos\left(a\right)}{8\cos^{2}\left(a\right)-1}&=&\dfrac{2\left(-2\sqrt{2}\cos\left(a\right)\right)}{1-\left(-2\sqrt{2}\cos\left(a\right)\right)^{2}} \\
&=&\tan\left(2\tan^{-1}\left(-2\sqrt{2}\cos\left(a\right)\right)\right) \\ \\ \\
\dfrac{4\sqrt{2}\cos\left(a\right)}{8\cos^{2}\left(a\right)-1}&=&\dfrac{\dfrac{-\dfrac{\left(\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}-0}{\dfrac{2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)}-\left(-1\right)}-\dfrac{-\dfrac{\left(\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}-0}{\dfrac{2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)}-\left(-1\right)}}{1+\dfrac{-\dfrac{\left(\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}-0}{\dfrac{2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)}-\left(-1\right)}\cdot\dfrac{-\dfrac{\left(\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}-0}{\dfrac{2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)}-\left(-1\right)}} \\
&=&\tan\left(\tan^{-1}\left(\dfrac{-\dfrac{\left(\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}-0}{\dfrac{2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)}-\left(-1\right)}\right)-\tan^{-1}\left(\dfrac{-\dfrac{\left(\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{1+\cos^{2}\left(a\right)}-0}{\dfrac{2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)}{1+\cos^{2}\left(a\right)}-\left(-1\right)}\right)\right) \\ \\ \\
\tan^{-1}\left(-2\sqrt{2}\cos\left(a\right)\right)&=&\tan^{-1}\left(\dfrac{\dfrac{\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-0}{\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-1}-\dfrac{\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-0}{\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-1}}{1+\dfrac{\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-0}{\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-1}\cdot\dfrac{\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-0}{\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-1}}\right) \\
&=&\tan^{-1}\left(\dfrac{\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)+\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-0}{\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)+\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)+4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-1}\right)-\tan^{-1}\left(\dfrac{\dfrac{-\cos\left(2a\right)\left(2\sin\left(a\right)-\sqrt{2}\right)\cos\left(a\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-0}{\dfrac{\cos\left(2a\right)\left(2\cos^{2}\left(a\right)-\sqrt{2}\sin\left(a\right)\right)}{2\cos^{2}\left(a\right)-4\sqrt{2}\sin\left(a\right)\cos^{2}\left(a\right)+1}-1}\right)
\end{eqnarray}$$
同様に、$Y$は直線$AF'$と直線$BF'$のなす角の大きさであり、すなわちその絶対値は$\angle AF'B$である。したがって、$\tan\left(X\right)=\tan\left(2Y\right)$を用いれば、$\angle CFD+180^{\circ}=2\angle AF'B$が導かれる($\because$図より$90^{\circ}<\angle AF'B<180^{\circ}$)。
あとがきには何を書いても良いと聞きました
さて、問題図のような状況においてつねに$\angle CFD+180^{\circ}=2\angle AF'B$が成立することは、かなり非自明であるように感じる。自身の具有する特別な性質に、天国のレムニスケート氏も満足してくれることだろう。
とはいえ、こういった性質には大抵先行研究が存在するものなので、ご存知の方が居ればコメントなどでご教示をねがう。万が一、いや万が$10^{-10000!}$、この性質を最初に発見したのが私であることを否定されないならば、親しみを込めて『レムちゃんの定理 ~ Il teorema inutile in lemniscata ~ 』と命名したい。