連続n整数の積で遊んでみた

今回は昔 $T E X$ (これやってみたかった笑)で書いたものをインポートしてみました。一応変になったりしたところは手直ししました。

この記事では、あの有名事実「連続n整数の積はn!で割り切れる」の証明についていろいろ考えていたときにたどり着いた、拡張のようなものを紹介します。遠回りだったり、洗練されていない表現だったりするかもしれませんが、その点はご容赦ください。

最終目標は次の定理です。

$d | n$ ならば
$\prod_{k = 0}^{m - 1} \frac{(x + k d)_{n}}{(k + 1)_{n}} = \frac{(x)_{n} (x + d)_{n} \dots (x + (m - 1) d)_{n}}{(1)_{n} (2)_{n} \dots (m)_{n}} \in Z$ である。

ただし、 $(x)_{n}$ はポッホハマー記号で、 $x (x + 1) \dots (x + n - 1)$ のことです。

まず、連続 $n$ 整数の中に自然数 $p$ で割り切れるものが何個あるかを考えます。始点を $x$ に選んだときのその個数を $f_{n, p} (x)$ としましょう。

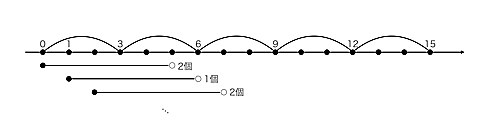p=3,n=5の例
(p=3,n=5の例)

$x$ を $p$ で割った余りを $R_{p} (x)$ とする。 $R_{p} (n) \neq 0$ のとき
$f_{n, p} (x) = {\begin{array}{rcl} ⌊ \frac{n}{p} ⌋ & (x \equiv 1, \dots, p - R_{p} (n) \mod p) \\ ⌊ \frac{n}{p} ⌋ + 1 & (x \equiv p - R_{p} (n) + 1, \dots, p \mod p) \end{array}$ であり、 $R_{p} (n) = 0$ のとき
$f_{n, p} (x) = ⌊ \frac{n}{p} ⌋$ である。

$I_{n} (x) = {x, x + 1, \dots, x + n - 1}$ を、右に１ずつずらしてゆく( $x$ を1ずつ増やしてゆく)ことを考える。そのときの $I_{n} (x)$ に属する $p$ の倍数の個数 $f_{n, p} (x)$ は、法を $p$ として、 $x \equiv 0$ から $x \equiv 1$ になるときに1減り、 $x \equiv - n$ から $x \equiv - n + 1$ になるときに1増える。また、 $x = 1$ のとき $f_{n, p} (1) = ⌊ \frac{n}{p} ⌋$ であるから、命題が成り立つ。

次の系が成り立ちます。

$R_{p} (n) \neq 0$ のとき $⌊ \frac{x + n}{p} ⌋ = {\begin{array}{rcl} ⌊ \frac{x}{p} ⌋ + ⌊ \frac{n}{p} ⌋ & (x \equiv 0, \dots, p - R_{p} (n) - 1 \mod p) \\ ⌊ \frac{x}{p} ⌋ + ⌊ \frac{n}{p} ⌋ + 1 & (x \equiv p - R_{p} (n), \dots, p - 1 \mod p) \end{array}$ であり、 $R_{p} (n) = 0$ のとき
$⌊ \frac{x + n}{p} ⌋ = ⌊ \frac{x}{p} ⌋ + ⌊ \frac{n}{p} ⌋$ である。

$\begin{array}{r} f_{n, p} (x) = ⌊ \frac{x + n - 1}{p} ⌋ - ⌊ \frac{x - 1}{p} ⌋ \end{array}$ より定理1から直ちに従う。

$d | n$ ならば $\sum_{k = 0}^{p - 1} f_{n, p} (x + k d) = n$ である。

$\begin{array}{rcl} \sum_{k = 0}^{p - 1} f_{n, p} (x + k d) & = & \sum_{k = 0}^{p - 1} (⌊ \frac{x + k d + n - 1}{p} ⌋ - ⌊ \frac{x + k d - 1}{p} ⌋) \\ = & \sum_{k = 0}^{p - 1} ⌊ \frac{x + k d + n - 1}{p} ⌋ - \sum_{k = 0}^{p - 1} ⌊ \frac{x + k d - 1}{p} ⌋ \end{array}$ ここで、 $x$ を $p$ で割った余りを $R_{p} (x)$ とすると、 $\begin{array}{rcl} \sum_{k = 0}^{p - 1} ⌊ \frac{x + k d - 1}{p} ⌋ & = & \sum_{k = 0}^{p - 1} (\frac{x + k d - 1}{p} - \frac{R_{p} (x + k d - 1)}{p}) \\ = & \sum_{k = 0}^{p - 1} \frac{x + k d - 1}{p} - \sum_{k = 0}^{p - 1} \frac{R_{p} (x + k d - 1)}{p} \end{array}$ であるから、 $\begin{array}{rcl} \sum_{k = 0}^{p - 1} & ⌊ \frac{x + k d + n - 1}{p} ⌋ - \sum_{k = 0}^{p - 1} ⌊ \frac{x + k d - 1}{p} ⌋ \\ = & (\sum_{k = 0}^{p - 1} \frac{x + k d + n - 1}{p} - \sum_{k = 0}^{p - 1} \frac{R_{p} (x + k d + n - 1)}{p}) - (\sum_{k = 0}^{p - 1} \frac{x + k d - 1}{p} - \sum_{k = 0}^{p - 1} \frac{R_{p} (x + k d - 1)}{p}) \\ = & (\sum_{k = 0}^{p - 1} \frac{x + k d + n - 1}{p} - \sum_{k = 0}^{p - 1} \frac{x + k d - 1}{p}) - (\sum_{k = 0}^{p - 1} \frac{R_{p} (x + k d + n - 1)}{p} - \sum_{k = 0}^{p - 1} \frac{R_{p} (x + k d - 1)}{p}) \\ = & n - \frac{1}{p} (\sum_{k = 0}^{p - 1} R_{p} (x + k d + n - 1) - \sum_{k = 0}^{p - 1} R_{p} (x + k d - 1)) \end{array}$ となる。 $k = 0, 1, \dots, p - 1$ において、 $x + k d - 1$ や $x + k d + n - 1$ は公差 $d$ の等差数列をなすが、それらは $n$ だけずれている。しかし $n$ は $d$ の倍数なので、それぞれの等差数列の各項を $p$ で割った余りは並び替えの関係にあり、登場する余りやその回数は完全に一致する。したがって、上式の第2項は0になり、 $\sum_{k = 0}^{p - 1} f_{n, p} (x + k d) = n$ が成り立つ。

${f_{n, p} (x + k d) | k = 0, 1, \dots, p - 1}$ の中で $⌊ \frac{n}{p} ⌋$ に等しいもの、および $⌊ \frac{n}{p} ⌋ + 1$ に等しいものの個数は、 $d | n$ なる $d$ に渡って一定である。

$a = ⌊ \frac{n}{p} ⌋, b = ⌊ \frac{n}{p} ⌋ + 1$ とすると、 $k a + l b = n$ かつ $k + l = p$ を満たす $k, l$ はただ１組に決まる(実際、 $(k, l) = (p b - n, - p a + n)$ となる)。命題2より、この $k, l$ が各個数であり、 $d$ によらない。

準備が整ったので、例の定理を証明します。

再掲

$d | n$ ならば
$\prod_{k = 0}^{m - 1} \frac{(x + k d)_{n}}{(k + 1)_{n}} = \frac{(x)_{n} (x + d)_{n} \dots (x + (m - 1) d)_{n}}{(1)_{n} (2)_{n} \dots (m)_{n}} \in Z$ である。

分母分子の素因数の個数を比較する。分子の素因数 $p$ の個数は
$\sum_{k = 0}^{m - 1} \sum_{e = 1}^{\infty} f_{n, p^{e}} (x + k d) = \sum_{e = 1}^{\infty} \sum_{k = 0}^{m - 1} f_{n, p^{e}} (x + k d)$ で与えられる。分母のそれは $d = 1, x = 1$ としたものに相当する。そこで、右辺の内側のシグマ、 $\sum_{k = 0}^{m - 1} f_{n, p^{e}} (x + k d)$ の値を $d, x$ の関数とみて、任意の $m, n, p, e$ でこれが $d = 1, x = 1$ で最小になることを示そう。簡単のため、 $a = ⌊ \frac{n}{p^{e}} ⌋, b = ⌊ \frac{n}{p^{e}} ⌋ + 1$ と書く。 $d = 1, x = 1$ において、 $k = 0, 1, \dots$ と動くとき、 $f_{n, p^{e}} (k + 1)$ は
$\overset{r}{\overset{⏞}{a, a, \dots, a}}, \overset{p^{e} - r}{\overset{⏞}{b, b, \dots, b}}, \underset{r}{\underset{⏟}{a, a, \dots, a}}, \underset{p^{e} - r}{\underset{⏟}{b, b, \dots, b}}, \dots$ となる。一般に、 $k = 0, 1, \dots$ と動くときの $f_{n, p^{e}} (x + k d)$ は、この数列の第 $x$ 項から $d$ 項おきに取り出したものである。ここで、命題3から、 $d | n$ ならばその数列は次のような性質を満たすことがわかっている。

( $a$ が $r$ 個, $b$ が $p^{e} - r$ 個),( $a$ が $r$ 個, $b$ が $p^{e} - r$ 個), $\dots$

さて、いま注目しているシグマは、この数列を第1項から第 $m$ 項まで足したものであるが、小さいもの( $a$ )から優先して足した方が小さくなることは明らかだから、 $d = 1, x = 1$ のときに最小になる。したがって、 $\sum_{e = 1}^{\infty} \sum_{k = 0}^{m - 1} f_{n, p^{e}} (x + k d) \geq \sum_{e = 1}^{\infty} \sum_{k = 0}^{m - 1} f_{n, p^{e}} (k + 1)$ が成り立つ。これは任意の素因数を分子が分母以上に持っていることを表し、定理は示された。