大学数学基礎解説

文献あり

区間縮小法の原理で「2乗して2になる正の実数（√2）」の存在を確認する

実数の連続性,解析学,実数

2525

Introduction

　高校の教科書などで紹介されている「 $\sqrt{2}$ は無理数」の証明について、「そもそも $2$ 乗して $2$ になる正の実数の存在が証明されていない」といった指摘を見かけます。

　今回は「区間縮小法の原理」を使いながら、 $2$ 乗して $2$ になる正の実数の存在を確認していきます。

　※中間値の定理ですぐ確認できる事実ではありますが、実数についての勉強もかねて、「区間縮小法の原理」を使ってみようと思います。

　※実数について、よくわかっていないので「これを仮定したらマズいよ」という性質を使っているようであれば、ぜひコメントなどください。

　※最初に本記事を公開したときには「 $\sqrt{2}$ は実数であることを確認する」といった表現をしていましたが、それでは「（実数なのかどうかわからないものではあるが） $\sqrt{2}$ が定義されていて、それが実数であることを示す」という意味合いになってしまうため、記事内の表現を一部変更しました（2022/6/20更新）

　※一意性についても追記しました（2022/6/20更新）

区間縮小法の原理

（実数の）閉区間の入れ子の列
$[a_{1}, b_{1}] \supseteq [a_{2}, b_{2}] \supseteq \dots \supseteq [a_{n}, b_{n}] \supseteq \dots$
において
$lim_{n \to \infty} (b_{n} - a_{n}) = 0$
が成立するならば、この区間列は（実数内に）ただ1つの共通要素をもつ。

（参考：藤田博司「『集合と位相』をなぜ学ぶのか」p.67）

「区間縮小法の原理」は、実数の連続性を表現する命題の1つとして知られていて、その他にも代表的な例として、以下のようなものがあります。

・＜ワイエルシュトラス連続の原理＞：上に有界な点集合には上限が存在する
・＜デデキントの切断の原理＞：実数の全体を左組と右組に切断するとき、その境界となる数が必ず存在する

（参考：藤田博司「『集合と位相』をなぜ学ぶのか」p.62）

上記について、お気持ち部分を解説しておきます。

高校の教科書などで「実数は数直線で表現できる」と学び、「途切れなくつながっている」などのイメージを持っている人が多いと思います。そのあたりについて、何となくのイメージでごまかすことなく、きちんと数学の言葉にしているのが、上記の命題たちである、と私は理解しています。

また、有理数では成り立たない命題なので、実数を特徴づけている性質である、とも認識しています。

ただ、私自身、実数について完璧に理解している自信はないので、この説明は「へー」程度に受け流しておいてください。

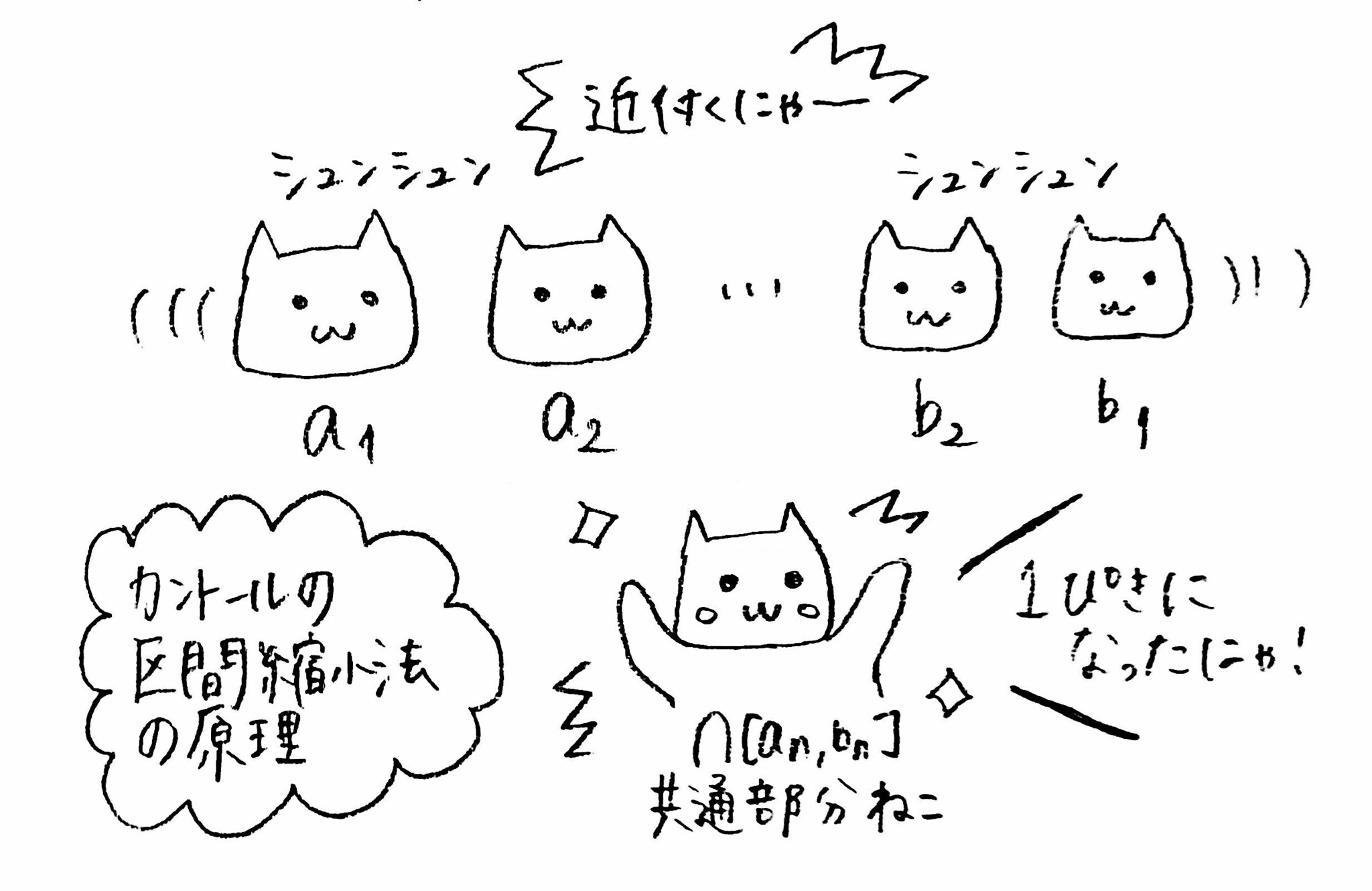ねこによるイメージ図

方針

ざっくりした方針は以下です。

集合 $A, B$ を以下とし、実数を2つに分けます。
$A = {x \in R | x ≦ 0 または x^{2} ≦ 2}$
$B = {x \in R | x > 0 かつ x^{2} > 2}$

$A ∋ 1, B ∋ 2$ をとり、 $a_{1} = 1, b_{1} = 2$ とします。これらの中点を $c_{1}$ とすると
$c_{1} = \frac{a_{1} + b_{1}}{2} = 1.5$
となり、 ${c_{1}}^{2} = 2.25 > 2$ なので、 $c_{1} \in B$ です。

次に、 $a_{1} = a_{2} \in A, b_{2} = c_{1} \in B$ とします。これらの中点を $c_{2}$ とすると
$c_{2} = \frac{a_{2} + b_{2}}{2} = 1.25$
となり、 ${c_{2}}^{2} = 1.5625 ≦ 2$ なので、 $c_{2} \in A$ です。

さらに次は、 $a_{3} = c_{2} \in A, b_{3} = b_{2} \in B$ とします。これらの中点をとり、 $A$ か $B$ どちらに属するか判定します。

これをくりかえします。つまり、 $a_{n} \in A, b_{n} \in B$ が与えられたとき、これらの中点 $c_{n}$ をとります。 $c_{n} \in A$ であるときは、 $a_{n + 1} = c_{n}, b_{n + 1} = b_{n}$ とし、 $c_{n} \in B$ であるときは、 $a_{n + 1} = a_{n}, b_{n + 1} = c_{n}$ とします。

このようにして、閉区間の入れ子
$[a_{1}, b_{1}] \supseteq [a_{2}, b_{2}] \supseteq \dots \supseteq [a_{n}, b_{n}] \supseteq \dots$
をつくり、その共通要素を調べます。

実際に計算をしてみると……

$[a_{n}, b_{n}]$ を $n = 1$ から $n = 30$ まで計算すると、以下のようになります。

[1.0,2.0]
[1.0,1.5]
[1.25,1.5]
[1.375,1.5]
[1.375,1.4375]
[1.40625,1.4375]
[1.40625,1.421875]
[1.4140625,1.421875]
[1.4140625,1.41796875]
[1.4140625,1.416015625]
[1.4140625,1.4150390625]
[1.4140625,1.41455078125]
[1.4140625,1.414306640625]
[1.4141845703125,1.414306640625]
[1.4141845703125,1.41424560546875]
[1.4141845703125,1.414215087890625]
[1.4141998291015625,1.414215087890625]
[1.41420745849609375,1.414215087890625]
[1.414211273193359375,1.414215087890625]
[1.4142131805419921875,1.414215087890625]
[1.4142131805419921875,1.41421413421630859375]
[1.4142131805419921875,1.414213657379150390625]
[1.4142134189605712890625,1.414213657379150390625]
[1.41421353816986083984375,1.414213657379150390625]
[1.41421353816986083984375,1.414213597774505615234375]
[1.41421353816986083984375,1.4142135679721832275390625]
[1.41421355307102203369140625,1.4142135679721832275390625]
[1.414213560521602630615234375,1.4142135679721832275390625]
[1.414213560521602630615234375,1.4142135642468929290771484375]
[1.414213560521602630615234375,1.41421356238424777984619140625]

$[{a_{n}}^{2}, {b_{n}}^{2}]$ を $n = 1$ から $n = 30$ まで計算すると、以下のようになります。

[1.0,4.0]
[1.0,2.25]
[1.5625,2.25]
[1.890625,2.25]
[1.890625,2.06640625]
[1.9775390625,2.06640625]
[1.9775390625,2.021728515625]
[1.99957275390625,2.021728515625]
[1.99957275390625,2.0106353759765625]
[1.99957275390625,2.005100250244140625]
[1.99957275390625,2.00233554840087890625]
[1.99957275390625,2.0009539127349853515625]
[1.99957275390625,2.000263273715972900390625]
[1.99991799890995025634765625,2.000263273715972900390625]
[1.99991799890995025634765625,2.0000906325876712799072265625]
[1.99991799890995025634765625,2.000004314817488193511962890625]
[1.99996115663088858127593994140625,2.000004314817488193511962890625]
[1.9999827356659807264804840087890625,2.000004314817488193511962890625]
[1.999993525227182544767856597900390625,2.000004314817488193511962890625]
[1.99999892001869739033281803131103515625,2.000004314817488193511962890625]
[1.99999892001869739033281803131103515625,2.0000016174171832972206175327301025390625]
[1.99999892001869739033281803131103515625,2.000000268717712970101274549961090087890625]
[1.99999959436814833679818548262119293212890625,2.000000268717712970101274549961090087890625]
[1.9999999315429164425950148142874240875244140625,2.000000268717712970101274549961090087890625]
[1.9999999315429164425950148142874240875244140625,2.000000100130311153634465881623327732086181640625]
[1.9999999315429164425950148142874240875244140625,2.00000001583661290993632064783014357089996337890625]
[1.9999999736897644542210628060274757444858551025390625,2.00000001583661290993632064783014357089996337890625]
[1.999999994763188626567540495670982636511325836181640625,2.00000001583661290993632064783014357089996337890625]
[1.999999994763188626567540495670982636511325836181640625,2.00000000529990075437414276393610634841024875640869140625]
[1.999999994763188626567540495670982636511325836181640625,2.0000000000315446870013946778499303036369383335113525390625]

「 $2$ 乗して $2$ になる正の実数」の存在

$c^{2} = 2$ を満たす正の実数 $c$ が（一意に）存在する。

集合 $A, B$ を以下とする。
$A = {x \in R | x ≦ 0 または x^{2} ≦ 2}$
$B = {x \in R | x > 0 かつ x^{2} > 2}$

$B = R ∖ A$ なので、どの実数も $A$ と $B$ のどちらか一方だけに入る。

また、 $A$ に属する任意の実数 $a$ は、 $B$ に属する任意の実数 $b$ よりも小さい（ $a < b$ ）。

$A ∋ 1, B ∋ 2$ をとり、 $a_{1} = 1, b_{1} = 2$ とする。

$a_{n} \in A, b_{n} \in B$ が与えられたときに、以下をくりかえす。

$a_{n}, b_{n}$ の中点を
$c_{n} = \frac{a_{n} + b_{n}}{2}$
とする。

$c_{n} \in A$ ならば、 $a_{n + 1} = c_{n}, b_{n + 1} = b_{n}$ とおく。

$c_{n} \in B$ ならば、 $a_{n + 1} = a_{n}, b_{n + 1} = c_{n}$ とおく。

これをくりかえし、閉区間の入れ子の列
$[a_{1}, b_{1}] \supseteq [a_{2}, b_{2}] \supseteq \dots \supseteq [a_{n}, b_{n}] \supseteq \dots$
をつくる。

$b_{n} - a_{n} = \frac{b_{1} - a_{1}}{2^{n - 1}} = \frac{1}{2^{n - 1}}$
より
$lim_{n \to \infty} (b_{n} - a_{n}) = 0$
が成り立つ（詳しくは、後述の補足参照）。

したがって、この区間列は（実数内に）ただ1つの共通要素をもつことがわかる。

この共通要素を $c$ とすると、任意の番号 $n$ に対し
$0 < a_{n} ≦ c ≦ b_{n} \dots (1)$
が成り立つ。

ここで、 $d_{n} = {a_{n}}^{2}, e_{n} = {b_{n}}^{2}$ とする。

$0 < a_{1} ≦ a_{2} ≦ \dots ≦ a_{n} ≦ b_{n} ≦ \dots ≦ b_{2} ≦ b_{1}$
より
$0 < d_{1} ≦ d_{2} ≦ \dots ≦ d_{n} ≦ e_{n} ≦ \dots ≦ e_{2} ≦ e_{1}$
である。

よって
$[d_{1}, e_{1}] \supseteq [d_{2}, e_{2}] \supseteq \dots \supseteq [d_{n}, e_{n}] \supseteq \dots$
となることがわかる。

また
$0 < e_{n} - d_{n} = {b_{n}}^{2} - {a_{n}}^{2} = (b_{n} - a_{n}) (b_{n} + a_{n})$
であることと
$(b_{n} - a_{n}) (b_{n} + a_{n}) ≦ \frac{(b_{1} - a_{1})}{2^{n - 1}} (b_{1} + b_{1}) = \frac{4}{2^{n - 1}} = \frac{1}{2^{n - 3}}$
であることから
$0 < e_{n} - d_{n} ≦ \frac{1}{2^{n - 3}}$
が成り立つ。

よって
$lim_{n \to \infty} (e_{n} - d_{n}) = 0$
であることがわかる（詳しくは、後述の補足参照）。

したがって、この区間列はただ1つの共通要素をもつことがわかる。

(1)より、任意の番号 $n$ に対し
${a_{n}}^{2} ≦ c^{2} ≦ {b_{n}}^{2}$
が成り立つので
$[d_{n}, e_{n}] ∋ c^{2}$
となり、この区間列のただ1つの共通要素は $c^{2}$ である。

また、 $A, B$ の定義から
${a_{n}}^{2} ≦ 2 < {b_{n}}^{2}$
が成り立つので
$[d_{n}, e_{n}] ∋ 2$
となり、この区間列のただ1つの共通要素は $2$ である。

したがって
$c^{2} = 2$
であることがわかる。

（一意性の証明）
$c$ とは異なる正の実数 $c^{'}$ が ${c^{'}}^{2} = 2$ を満たすと仮定して、背理法で示す。

このとき、任意の番号 $n$ について
${a_{n}}^{2} ≦ {c^{'}}^{2} < {b_{n}}^{2}$
より
$(0 <) a_{n} ≦ c^{'} < b_{n}$
が成り立つ。

したがって $c^{'}$ は区間列 $[a_{n}, b_{n}]$ の共通要素であることがわかる。

しかし、この区間列の共通要素は $c$ ただ1つであるため、矛盾。

よって、 $2$ 乗して $2$ となる正の実数は $c$ ただ1つであることが示された。

※以上の証明は、藤田博司「『集合と位相』をなぜ学ぶのか」pp.67-68に書かれている「区間縮小法の原理から切断の原理を導く」を参考にしました。

デデキントの切断の原理、ワイエルシュトラス連続の原理

任意の番号 $n$ に対し、 $a_{n} \in Q, b_{n} \in Q$ ですが、区間列のただ1つの共通要素である $c$ は有理数ではありません。

また、集合 $A, B$ は

1.どの実数も $A, B$ のどちらか一方だけに入る
2. $A$ に属するどの数 $a$ も、 $B$ に属するどの数 $b$ よりも小さい $(a < b)$

（参考：藤田博司「『集合と位相』をなぜ学ぶのか」p.63）

を満たすので、 $A$ と $B$ の組は、実数の切断であり、 $A$ は左組、 $B$ は右組となっています。

$c$ は $A$ の最大要素で、左組と右組の境界となっていることがわかります（「デデキントの切断の原理」の確認）。 $B$ の最小要素は存在しません。

下記の「デデキントキャットされました」イラストで言うところの、上（最大ねこがいる方）に相当しています。

デデキントキャット

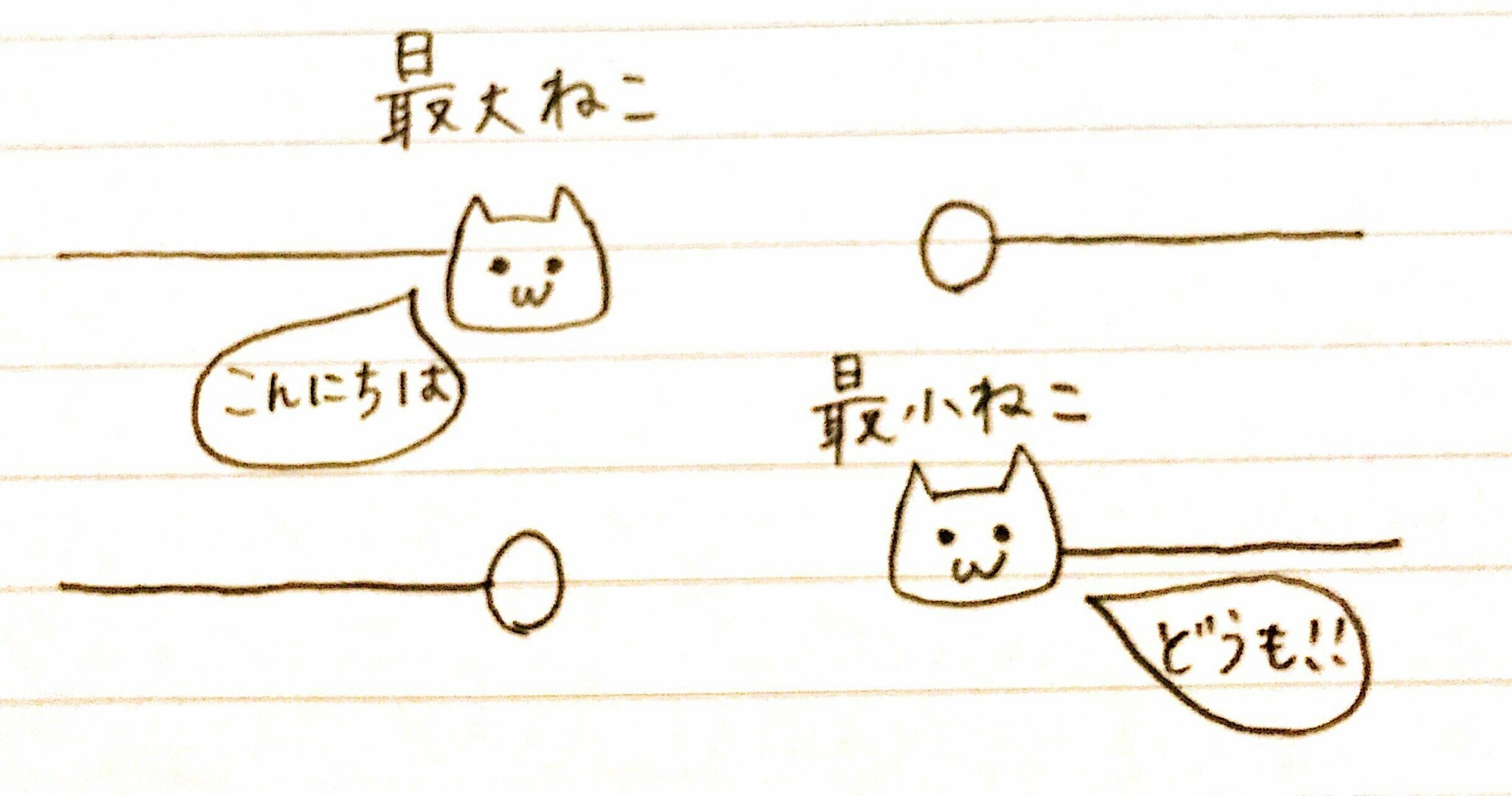デデキントキャットされました

一方、有理数をデデキントキャットすると…？

また、 $A$ は上に有界であり、 $c$ が $A$ の上限であることもわかります（「ワイエルシュトラス連続の原理」の確認）。

補足

証明の中で
$lim_{n \to \infty} \frac{1}{2^{n}} = 0$
を使っているので、これを示しておきます。

$1$ 以上の任意の整数 $n$ に対して
$n < 2^{n}$
が成り立つ。

数学的帰納法で証明する。

$n = 1$ のとき
$1 < 2$
より、成立する。

$n = k$ のとき
$k < 2^{k} \dots (1)$
が成立すると仮定する。

(1)の両辺に $2$ をかけて
$2 k < 2^{k + 1} \dots (2)$
となる。

また
$1 ≦ k$
より

$1 ≦ 2 k - k$ 　
なので

$k + 1 ≦ 2 k \dots (3)$
である。

(2)(3)より
$k + 1 ≦ 2 k < 2^{k + 1}$
となるので、 $n = k$ のときも成り立つことがわかる。

以上より、 $1$ 以上の任意の整数 $n$ に対して
$n < 2^{n}$
が成り立つ。

$lim_{n \to \infty} \frac{1}{2^{n}} = 0$
が成り立つ。

$ε$ を任意の正の実数とする。

アルキメデス性より、ある $1$ 以上の整数 $n_{ε}$ が存在して
$(0 <) \frac{1}{ε} < n_{ε}$
を満たす。

よって、 $n > n_{ε}$ を満たす、 $1$ 以上の整数 $n$ について
$\frac{1}{ε} < n$
が成り立つ。

したがって
$\frac{1}{n} < ε \dots (4)$
となる。

補題2より
$\frac{1}{2^{n}} < \frac{1}{n} \dots (5)$
である。

(4)(5)より
$\frac{1}{2^{n}} < ε$
が成り立つ。

以上より、任意の正の実数 $ε$ に対し、ある $1$ 以上の整数 $n_{ε}$ が存在して、 $n > n_{ε}$ ならば
$\frac{1}{2^{n}} < ε$
が成り立つので
$lim_{n \to \infty} \frac{1}{2^{n}} = 0$
であることが示された。

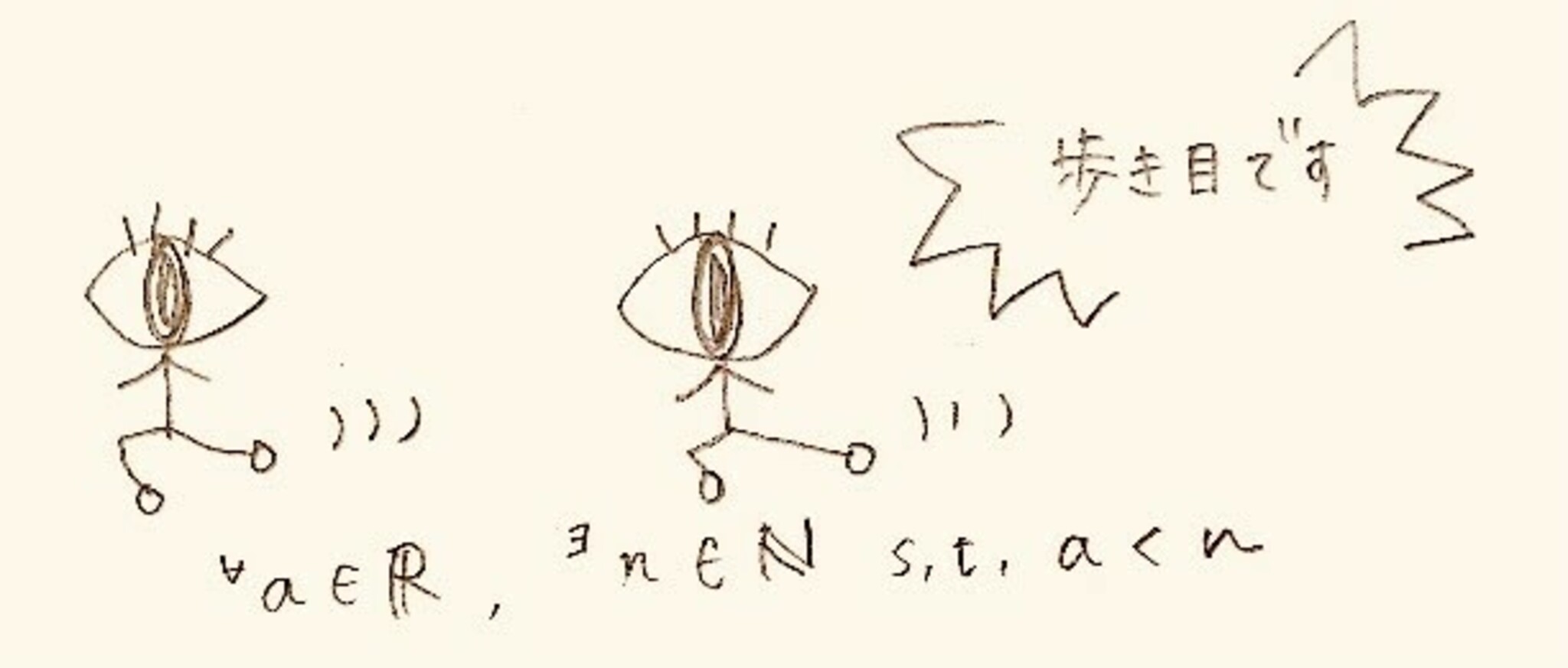歩き目です性

感想

　実数の順序や演算について、きちんと勉強した記憶がなく、今回証明していても「この性質、本当に使って良いのか？」と、1つ1つ疑心暗鬼になっていたので、いつかその辺りも頑張ってみたいです。

　実数と仲良くなりたい！

参考文献

[1]

藤田博司, 「集合と位相」をなぜ学ぶのか ―数学の基礎として根づくまでの歴史

投稿日：2022年6月17日

更新日：2023年11月30日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

みぽ

164

34489

今日もねこがかわいい。

他の人のコメント

コメントはありません。

読み込み中

みぽ

区間縮小法の原理で「2乗して2になる正の実数（√2）」の存在を確認する

Introduction
区間縮小法の原理
方針
実際に計算をしてみると……
「 $2$ 乗して $2$ になる正の実数」の存在
デデキントの切断の原理、ワイエルシュトラス連続の原理
補足
感想
参考文献

区間縮小法の原理で「2乗して2になる正の実数（√2）」の存在を確認する

Introduction

区間縮小法の原理

方針

実際に計算をしてみると……

「2乗して2になる正の実数」の存在

デデキントの切断の原理、ワイエルシュトラス連続の原理

補足

感想

参考文献

この記事を高評価した人

この記事に送られたバッジ

投稿者

コメント

他の人のコメント

「 $2$ 乗して $2$ になる正の実数」の存在