2
解説大学数学以上
複素積分11
$$$$
今回は こちら の積分を解説します。
レイアウトとか気にかけていますが、乗っ取られてはいません。安心してください。
モチベーションは少し回復してきました。
$\displaystyle\int_0^∞\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx=\frac{\pi}{2b^4e^{\frac{ab}{\sqrt{2}}}}\sin{\frac{ab}{\sqrt{2}}}$
解説
複素関数$\displaystyle f(z):=\frac{e^{-az}}{z(z^4+b^4)}$を次の領域で周回積分します。
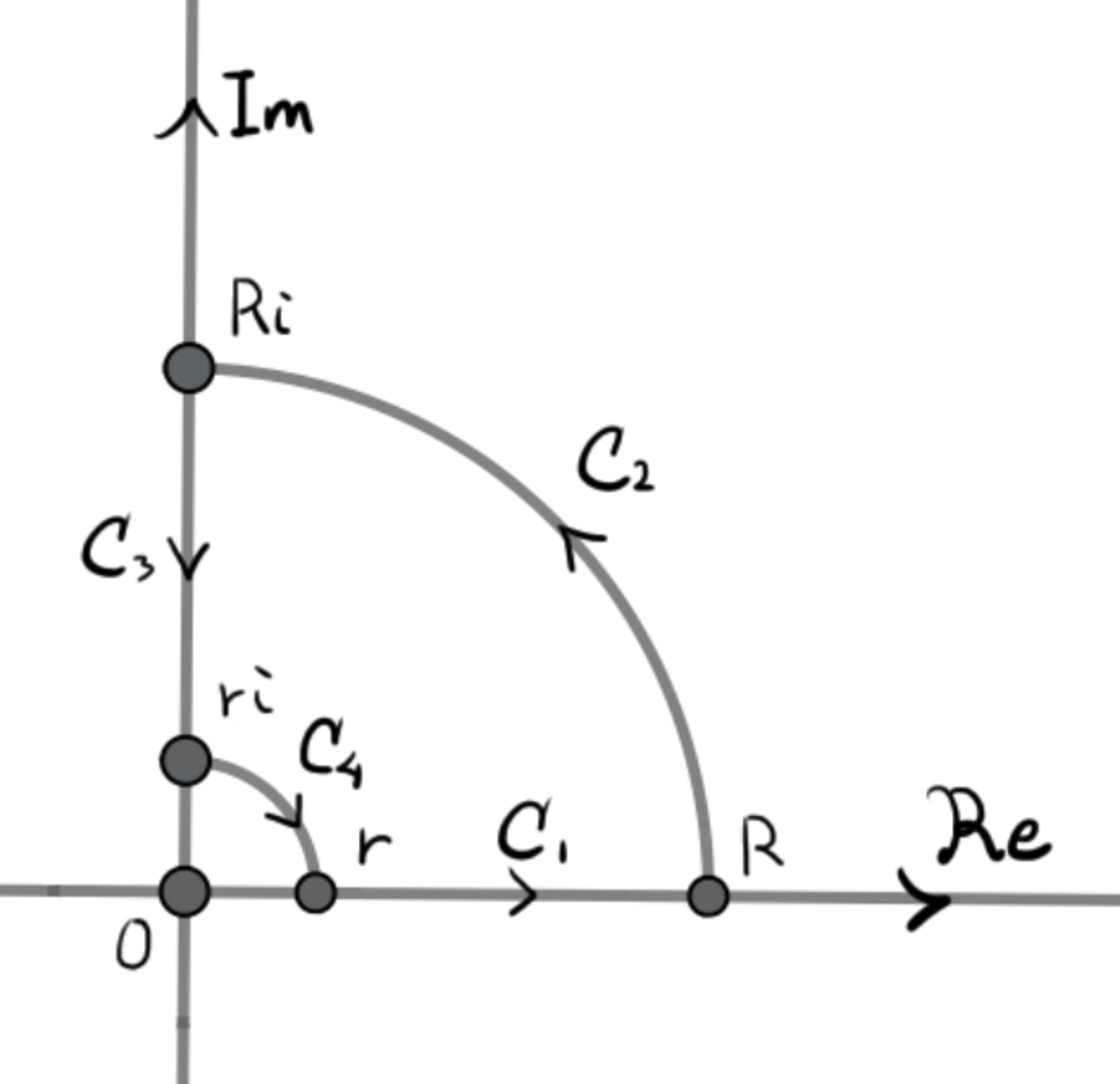複素積分を行う領域
ここで$\displaystyle r→0,R→∞$とします。
$\displaystyle\int_{C_1}=\int_0^∞\frac{e^{-ax}}{x(x^4+b^4)}dx \quad \displaystyle\int_{C_2}=0 \\ \displaystyle\int_{C_3}=\int_∞^0\frac{e^{-aix}}{ix\big((ix)^4+b^4\big)}\big(idx\big) \quad \displaystyle\int_{C_4}=0 $
尚、$C_2,C_4$はジョルダンの補題を用いました
周回積分を求めましょう。
$\begin{eqnarray} \displaystyle\oint_C &=& 2\pi i\lim_{z\to b\sqrt{i}}\frac{e^{-az}}{z(z^4+b^4)}\big(z-b\sqrt{i}\big) \\ \displaystyle &=& 2\pi i\frac{e^{-ab\sqrt{i}}}{b\sqrt{i}･2b^2i･2b\sqrt{i}} \\ \displaystyle &=& -\frac{\pi i}{2b^4e^\frac{ab}{\sqrt{2}}}e^{-\frac{ab}{\sqrt{2}}i} \end{eqnarray}$
$\begin{eqnarray} \displaystyle\therefore\int_0^∞\frac{\cos ax-e^{-ax}}{x(x^4+b^4)}dx &=& -\Re\int_{C_1+C_2+C_3+C_4} \\ \displaystyle &=& -\Re\oint_C \\ \displaystyle &=& \frac{\pi}{2b^4e^\frac{ab}{\sqrt{2}}}\sin{\frac{ab}{\sqrt{2}}} \end{eqnarray}$
投稿日：2022年6月18日
投稿者
投稿者
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
コメント
コメント