コスニタの定理の初等的な証明

初等幾何

944

はじめに

mathlogのこちらの記事でコスニタの定理というものを見かけて, それの初等的な証明を思いついたので紹介します. なお, 引用元の記事も, とてもたくさん幾何の知識が紹介されていて素敵な記事なのでオススメです！

証明

コスニタの定理

外心を $O$ とする三角形 $A B C$ において, 三角形 $O B C, O C A, O A B$ の外心をそれぞれ $O_{A}, O_{B}, O_{C}$ とすると $A O_{A}, B O_{B}, C O_{C}$ は一点で交わる.

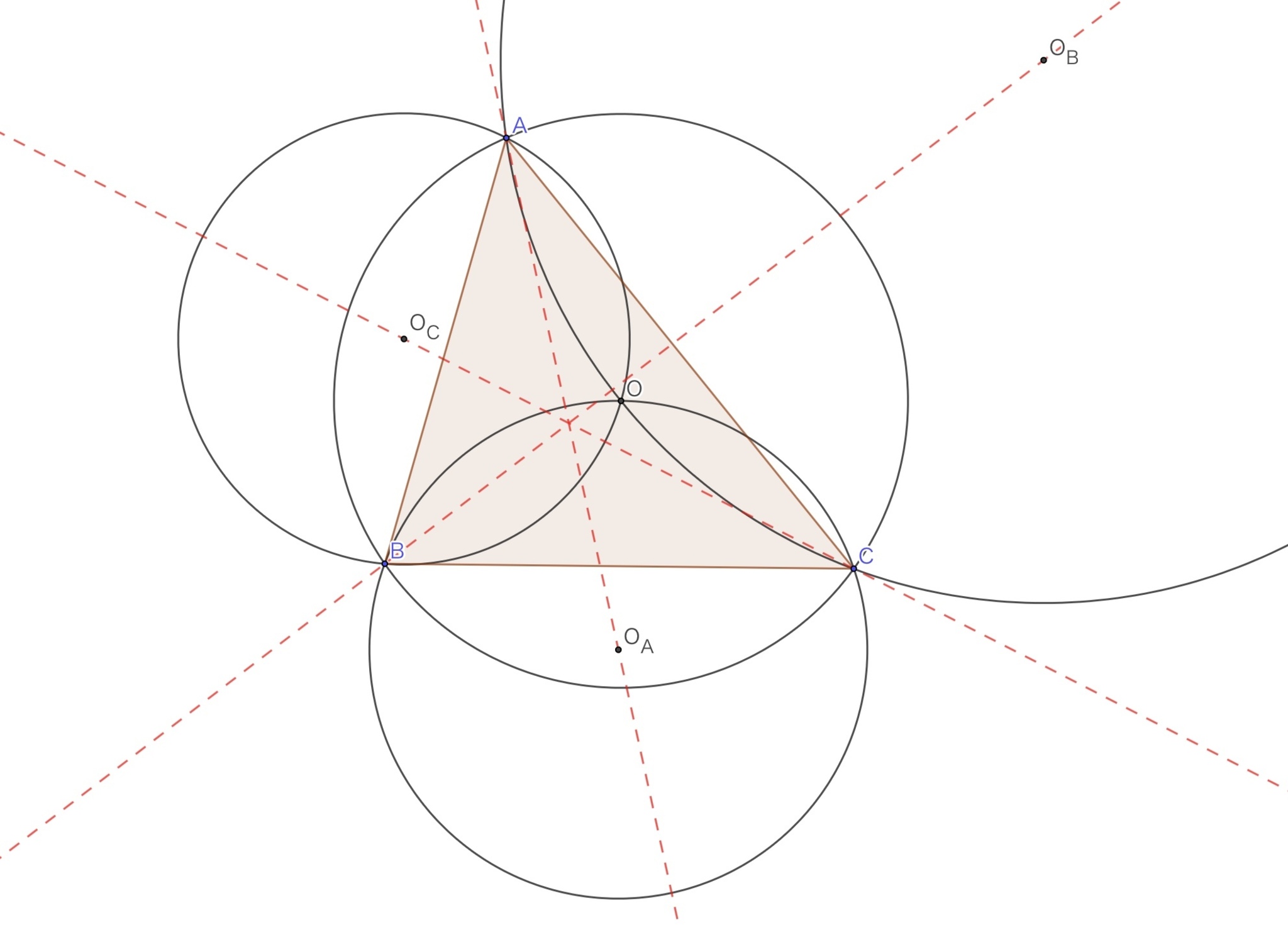
それでは証明していきます. まず, $O$ を $B C$ に関して対称移動させた点を $D$ とすると,
$∠ B O D = ∠ O_{A} O B, ∠ O D B = ∠ D O B = ∠ O B O_{A}$
より三角形 $O D B$ と $O B O_{A}$ は相似なので, 対応辺の比から $O B^{2} = O D \cdot O O_{A}$ を得ます. すなわち $D$ は $O_{A}$ を三角形 $A B C$ の外接円に関して反転させた点と一致します. よって直線 $O O_{A}$ と三角形 $A B C$ の外接円との交点のうち, 線分 $O_{A} D$ 内にあるものを $P$ , そうでないものを $Q$ とすると, $(O_{A}, D; P, Q)$ は調和点列となっているので, 三角形 $A B C$ の外接円は $2$ 点 $O_{A}, D$ のアポロニウスの円となっており, 特に $∠ O_{A} A P = ∠ D A P$ を得ます.したがって直線 $A O_{A}, A D$ は三角形 $A B C$ の角 $A$ 内における等角共役の関係にあることがわかります.

ここで次の補題を用意します:

外心を $O$ とする三角形 $A B C$ において, $O$ と辺 $B C, C A, A B$ に関して対称な点をそれぞれ $D, E, F$ としたとき $A D, B E, C F$ は一点で交わる.

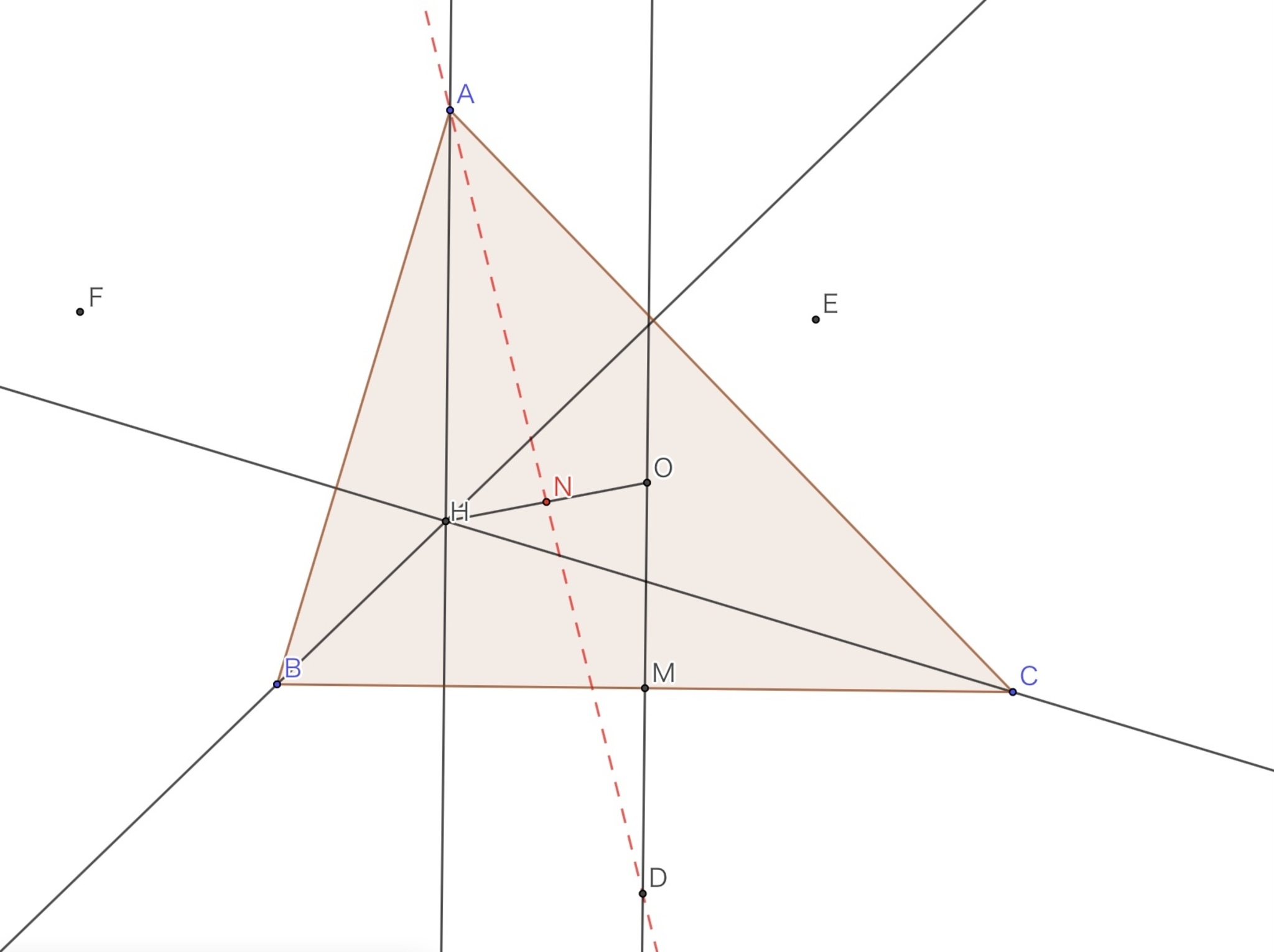
三角形 $A B C$ の垂心を $H$ , $B C$ の中点を $M$ とすると, $A H$ と $O D$ は平行であり, かつ $A H = 2 O M = O D$ (証明略)であるから, $A H D O$ は平行四辺形である. よって $A D$ は $O H$ の中点 $N$ (これは三角形 $A B C$ の九点円の中心である)を通り, 同様にして $B E, C F$ も $N$ を通ることがわかるから題意は示された.